Автор: Денис Аветисян
В новой работе исследованы релятивистские эффекты, влияющие на минимальное время, необходимое для изменения квантового состояния, и предложены способы экспериментальной проверки этих эффектов.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал
В статье получены поправки первого порядка к квантовому пределу скорости для когерентных и сжатых состояний, а также разработан подход к экспериментальной верификации с использованием сбалансированной гомодинной детекции.
Существующие оценки квантового предела скорости, критически важные для прецизионных измерений времени и фазы, как правило, не учитывают релятивистские эффекты. В работе «Релятивистский квантовый предел скорости для гауссовых систем и перспективная экспериментальная проверка» получены поправки первого порядка к пределам Мандельштама-Тама и Марголуса-Левитина для когерентных и сжатых состояний. Показано, что релятивистская кинематика влияет на эволюцию состояния и фазовую чувствительность, а также предсказано наличие дрейфа фазы, потенциально обнаружимого в экспериментах с использованием сжатых состояний и гомодинного детектирования. Может ли предложенный подход открыть новые возможности для тестирования фундаментальных ограничений на скорость эволюции квантовых систем в экстремальных условиях?
Фундаментальные границы квантовой динамики
Скорость эволюции квантовых состояний играет фундаментальную роль в широком спектре современных технологий. От скорости вычислений в квантовых компьютерах, где быстрая манипуляция кубитами критически важна для решения сложных задач, до точности измерений в квантовой метрологии, где быстрое изменение состояний позволяет достичь беспрецедентной чувствительности. Понимание этих скоростных ограничений необходимо для разработки эффективных квантовых алгоритмов и высокоточных сенсоров. Например, в квантовой криптографии скорость, с которой меняются состояния фотонов, напрямую влияет на безопасность передачи информации. Более того, в области квантовой химии и материаловедения, скорость эволюции волновых функций определяет динамику химических реакций и свойства материалов. Таким образом, исследование и оптимизация скорости квантовой эволюции является ключевой задачей для дальнейшего развития квантовых технологий и углубления понимания фундаментальных законов природы.
В квантовой механике интуитивные представления о скорости и траекториях, сформированные в классической физике, оказываются неприменимыми. Представление о четко определенной скорости частицы в определенный момент времени уступает место вероятностному описанию, где положение и импульс связаны принципом неопределенности Гейзенберга. Это требует разработки строгого математического аппарата для определения фундаментальных ограничений на эволюцию квантовых состояний. Классические границы, основанные на понятии определенной траектории, здесь не работают, и необходимо учитывать вероятностную природу квантовых явлений, что приводит к появлению новых ограничений, отличающихся от тех, которые известны в классической физике. Поэтому, для точного описания и прогнозирования поведения квантовых систем, требуется принципиально иной подход, основанный на строгих математических принципах и учитывающий вероятностную природу квантовых явлений.
Принципиальное ограничение на скорость эволюции квантовых состояний устанавливается соотношением неопределенностей между временем и энергией, однако для реализации практических квантовых технологий требуются более точные оценки. Традиционное выражение этого соотношения недостаточно для описания процессов, протекающих со скоростями, близкими к скорости света. Релятивистские поправки вносят существенный вклад, изменяя границы допустимых скоростей эволюции квантовых систем на величины, пропорциональные $ϵ^2t^2$, где $ϵ$ представляет собой отношение скорости к скорости света, а $t$ — время. Эти поправки особенно важны при проектировании высокоскоростных квантовых вычислений и точных измерений, поскольку они определяют минимальное время, необходимое для выполнения квантовых операций и достижения требуемой точности.
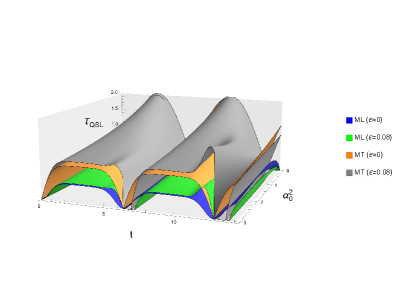
Квантовые состояния и границы скорости
Предел скорости в квантовой механике не является универсальной константой, а зависит от конкретного квантового состояния системы. Например, для когерентных состояний ($|\alpha\rangle$) и выжатых состояний ($|r, \theta\rangle$) пределы скорости эволюции различаются. Когерентные состояния характеризуются равномерным распределением неопределенностей в фазе и амплитуде, в то время как выжатые состояния демонстрируют уменьшение неопределенности в одной из этих переменных за счет увеличения неопределенности в другой. Данное различие в распределении неопределенностей приводит к различным значениям минимального времени, необходимого для эволюции системы из одного состояния в другое, определяемого, в частности, неравенствами Мандельштама-Тама и Марголуса-Левитина.
Использование оператора сжатия (squeeze operator) для создания сжатых состояний ($ squeezed states$) позволяет, в принципе, достичь более быстрой эволюции квантовой системы по сравнению с использованием только когерентных состояний. Это связано с тем, что оператор сжатия изменяет неопределённости в квадратурах электромагнитного поля, уменьшая неопределенность в одной квадратуре за счет увеличения в другой. Такое изменение позволяет обойти ограничения, накладываемые стандартным квантовым пределом скорости, поскольку скорость эволюции обратно пропорциональна неопределенности. В результате, для заданного изменения состояния, сжатые состояния могут эволюционировать быстрее, чем когерентные состояния, хотя это и не нарушает фундаментальные принципы квантовой механики.
Пределы скорости эволюции квантовой системы определяются не только общим квантовым пределом, но и конкретным состоянием системы. Ограничения $Mandelstam-Tamm$ и $Margolus-Levitin$ предоставляют более жесткие, зависящие от состояния границы максимальной скорости эволюции. В частности, при рассмотрении сжатых состояний ($Squeezed States$), эти границы модифицируются релятивистскими поправками первого порядка. Эти поправки оказывают влияние на дисперсию сжатых состояний, изменяя допустимую скорость эволюции и, следовательно, уточняя пределы, установленные ограничениями $Mandelstam-Tamm$ и $Margolus-Levitin$. Таким образом, учет релятивистских эффектов необходим для точного определения максимальной скорости эволюции квантовых систем, находящихся в сжатых состояниях.
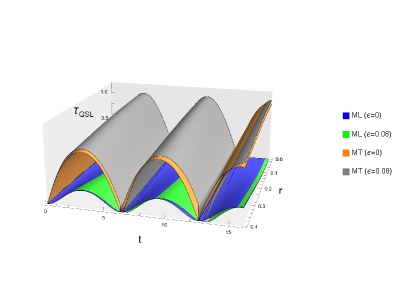
Прецизионные измерения и квантовый предел скорости
Для определения скорости квантовой эволюции необходимо проводить точные измерения изменений состояния системы. Одним из часто используемых методов для этой цели является $Balanced\ Homodyne\ Detection$ (сбалансированное гомодинное детектирование). Данная техника позволяет измерять квадратуры электромагнитного поля с высокой точностью, что критически важно для отслеживания даже незначительных изменений квантового состояния. Принцип работы метода основан на интерференции сигнала с локальным осциллятором, что позволяет реконструировать информацию о фазе и амплитуде сигнала. Выбор оптимальных параметров локального осциллятора и эффективная обработка полученных данных являются ключевыми факторами для достижения высокой точности измерений скорости квантовой эволюции.
Прецизионность измерения параметров квантового состояния фундаментально ограничена границей Крамера-Рао (Cramer-Rao Bound), которая представляет собой нижнюю границу дисперсии любой несмещенной оценки параметра. Эта граница напрямую связана с квантовой информацией Фишера (Quantum Fisher Information, QFI), которая, по сути, характеризует количество информации о параметре, содержащееся в квантовом состоянии. QFI определяется как минимальное значение дисперсии любого оператора, действующего на состояние, и обратно пропорциональна точности, с которой можно оценить параметр. Таким образом, максимизация QFI посредством оптимизации стратегии измерения позволяет приблизиться к теоретическому пределу точности, определяемому границей Крамера-Рао. Математически, граница Крамера-Рао выражается как $1/\text{Variance}(\hat{\theta}) \geq \text{QFI}$, где $\hat{\theta}$ — оценка измеряемого параметра.
Оптимизация стратегий измерений позволяет приближаться к теоретическим пределам, определяемым квантовым пределом скорости и ограничениями на точность измерений. При этом необходимо учитывать детерминированный сдвиг фазы, вызванный релятивистскими эффектами, который количественно оценивается как $γt^2$, где γ — фактор Лоренца, а t — время. Достижение максимальной точности требует минимизации влияния этого сдвига фазы посредством выбора оптимальных параметров измерения и коррекции полученных данных. Выбор стратегии измерения должен учитывать как квантовые ограничения, определяемые квантовой информацией Фишера, так и влияние релятивистских эффектов на динамику квантовой системы.
Релятивистские эффекты и фазовая чувствительность
В высокоточных квантовых системах релятивистские поправки приобретают решающее значение, оказывая заметное влияние на наблюдаемую фазовую чувствительность. В то время как классическая квантовая механика часто обеспечивает адекватное описание, при работе с частицами, движущимися со скоростями, сравнимыми со скоростью света, или в сильных полях, пренебрежение релятивистскими эффектами приводит к значительным погрешностям. Эти поправки, учитывающие изменения массы и времени, предсказанные специальной теорией относительности, проявляются как смещение фазы квантового состояния, которое может быть экспериментально измерено. Величина этого смещения пропорциональна квадрату времени и квадрату параметра $\epsilon$, отражающего относительную величину релятивистских эффектов, что делает фазовую чувствительность ключевым индикатором необходимости учета релятивистской коррекции в прецизионных измерениях и квантовых технологиях.
Разложение Фольди-Вутхуйзена представляет собой систематический подход к включению релятивистских поправок в расчеты квантовой динамики. Данный метод позволяет последовательно учитывать эффекты, возникающие из специальной теории относительности, в уравнениях движения квантовых систем. В основе разложения лежит разделение волновой функции на «большие» и «малые» компоненты, что позволяет исключить нежелательные члены, связанные с высокой скоростью частиц. Благодаря этому, вычисления становятся более точными, особенно в ситуациях, когда энергия частиц приближается к массе покоя или в сильных полях. Применение разложения Фольди-Вутхуйзена критически важно для моделирования процессов в физике высоких энергий, атомной физике и квантовой химии, где пренебрежение релятивистскими эффектами может привести к значительным погрешностям в результатах.
В высокоточных квантовых системах, особенно с участием частиц высоких энергий или в сильных полях, релятивистские поправки способны модифицировать эффективный предел квантовой скорости. Данное явление приводит к измеримому сдвигу фазы, который растет квадратично со временем — пропорционально $γt^2$, где γ — фактор Лоренца, характеризующий релятивистские эффекты. Этот сдвиг фазы также пропорционален $ϵ^2t^2$, где ϵ представляет собой величину, отражающую интенсивность внешнего поля или энергию частицы. Такая зависимость от квадрата времени позволяет не только наблюдать, но и количественно оценивать вклад релятивистских эффектов, открывая возможности для новых прецизионных измерений и контроля над квантовыми системами.
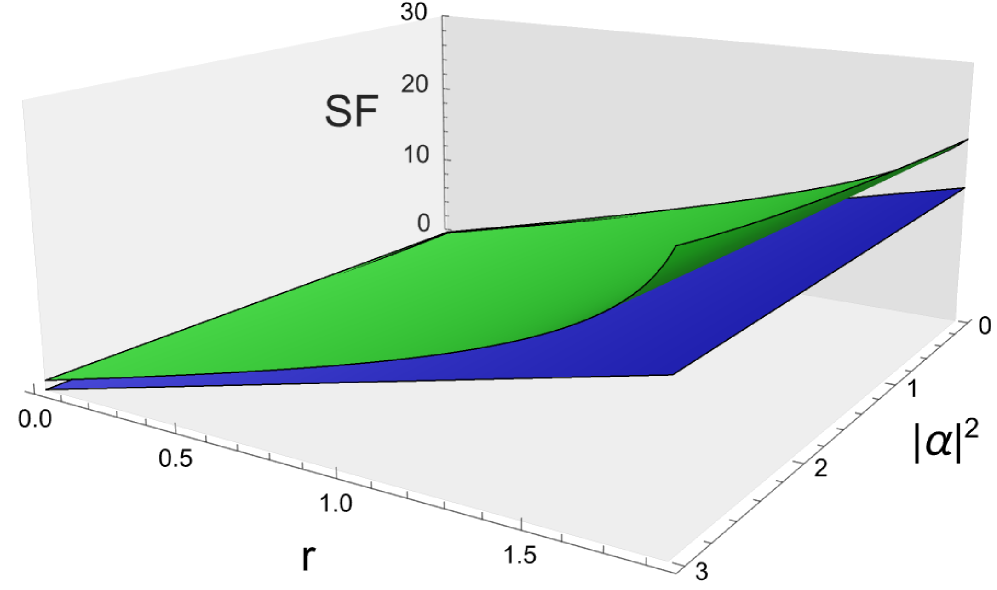
Применение в квантовой связи
Современные протоколы безопасной связи, такие как GMCS CV-QKD, базируются на фундаментальной необходимости точного управления квантовыми состояниями и прецизионной оценке фазы. В этих системах информация кодируется в квантовых свойствах частиц, например, в амплитуде и фазе света, что делает их потенциально неуязвимыми для перехвата. Однако, малейшие отклонения в фазе сигнала, вызванные шумами и несовершенством оборудования, могут привести к ошибкам при декодировании и, следовательно, к компрометации безопасности связи. Поэтому, разработка методов, обеспечивающих высокую точность оценки фазы, является критически важной задачей для практической реализации квантовой криптографии и защиты конфиденциальной информации. Успешная реализация таких протоколов напрямую зависит от способности поддерживать когерентность квантовых состояний и минимизировать влияние факторов, искажающих фазу сигнала.
Для обеспечения надежной квантовой связи, такой как протоколы $GMCS CV-QKD$, критически важна компенсация фазовых ошибок, возникающих из-за нестабильности каналов связи и несовершенства оборудования. Методы пилот-слежения за фазой позволяют эффективно бороться с этими ошибками, используя заранее известные квантовые состояния — “пилоты” — для калибровки и коррекции фазовых сдвигов. Благодаря применению пилот-слежения удается значительно повысить точность оценки фазы и, как следствие, увеличить скорость генерации секретного ключа — ключевой показатель эффективности квантовой криптографии. Эффективность этих методов напрямую влияет на дальность и надежность квантовых коммуникационных систем, делая их неотъемлемой частью современных и перспективных разработок в области квантовой связи.
Для полной реализации потенциала квантовой связи необходимо преодолеть фундаментальные ограничения, связанные со скоростью квантовых измерений и их точностью. Исследования показывают, что при достижении предельно высокой точности измерений фазы, становится возможным обнаружение релятивистского дрейфа фазы — эффекта, обусловленного влиянием теории относительности — всего за приблизительно 15 минут усреднения данных. Данное достижение открывает путь к созданию сверхстабильных квантовых каналов связи, устойчивых к воздействию гравитационных и релятивистских факторов, что критически важно для построения глобальных квантовых сетей и обеспечения абсолютно безопасной передачи информации на большие расстояния. Повышение точности и скорости квантовых измерений является ключевой задачей для развития практических приложений квантовых технологий.
Исследование, представленное в данной работе, стремится к очищению понимания фундаментальных границ скорости квантовых процессов. Авторы, подобно скульпторам, отсекают избыточное, чтобы выявить истинную форму пределов, накладываемых релятивистскими эффектами на когерентные и сжатые состояния. Особое внимание к фазовой чувствительности и возможности экспериментальной проверки посредством сбалансированной гомодинной детекции подчеркивает стремление к ясности и точности. Как заметил Нильс Бор: «Противоположности не противоречат, а дополняют друг друга». Именно в этом дополнении, в учете как квантовых, так и релятивистских аспектов, заключается глубина и ценность представленного исследования. Отказ от усложнения ради усложнения позволяет увидеть суть — пределы скорости, определяющие границы познания.
Куда же дальше?
Представленные выкладки, как и любое уточнение границ дозволенного, лишь обнажают невежество, скрывающееся за кажущейся точностью. Первый порядок релятивистских поправок к пределу скорости квантового перемещения — это, конечно, шаг. Но сама идея «предела скорости» для системы, чье состояние описывается вероятностью, изначально вызывает легкую иронию. Настоящая сложность, как всегда, кроется не в вычислениях, а в интерпретации. Какова физическая значимость этих поправок, когда речь идет о когерентных и сжатых состояниях, подверженных шуму, неизбежно присутствующему в любой реальной системе?
Экспериментальная проверка с использованием сбалансированной гомодинной детекции — это необходимое, но недостаточное условие. Более глубокое понимание потребует не просто измерения фазовой чувствительности, а анализа того, как эти релятивистские эффекты влияют на квантовую запутанность и декогеренцию. И, возможно, потребуется переосмыслить саму концепцию «оптимальной» траектории в квантовом пространстве состояний. Система, требующая подробных инструкций для демонстрации своих возможностей, уже проиграла.
Понятность — это вежливость. И в данном случае, истинное величие этой работы заключается не в полученных формулах, а в том, что она, как и любая хорошая работа, ставит больше вопросов, чем дает ответов. Путь к более глубокому пониманию квантовой механики лежит через признание границ нашего знания, а не через их иллюзорное расширение.
Оригинал статьи: https://arxiv.org/pdf/2511.20707.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Все рецепты культистского круга в Escape from Tarkov
- Где находится точка эвакуации «Туннель контрабандистов» на локации «Интерчейндж» в Escape from Tarkov?
- Как получить скины Alloyed Collective в Risk of Rain 2
- Для чего нужен тотем жертвоприношений в игре 99 ночей в лесу?
- Где посмотреть ‘Five Nights at Freddy’s 2’: расписание сеансов и статус потоковой передачи.
- Решение головоломки с паролем Absolum в Yeldrim.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Руководство по целительской профессии в WWM (Where Winds Meet)
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Как пройти I’m Not a Robot – полное прохождение всех уровней
2025-11-27 13:52