Квантовые состояния по запросу: новый метод генерации неклассического света

от

Автор: Денис Аветисян

Исследователи разработали универсальный метод генерации не-гауссовых квантовых состояний света с помощью оптического параметрического усилителя, открывая новые возможности для квантовых технологий.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал
С использованием оптического параметрического усилителя создаются не-гауссовы квантовые состояния, причём в сигнальный канал вводятся специфические состояния, такие как сжатый вакуум или кошачьи состояния малого размера, а одиночный фотон подаётся в канал рассеяния; регистрация этого фотона на выходе служит сигналом о создании не-гауссова состояния в сигнальном канале, характеристики которого регулируются изменением усиления усилителя.
С использованием оптического параметрического усилителя создаются не-гауссовы квантовые состояния, причём в сигнальный канал вводятся специфические состояния, такие как сжатый вакуум или кошачьи состояния малого размера, а одиночный фотон подаётся в канал рассеяния; регистрация этого фотона на выходе служит сигналом о создании не-гауссова состояния в сигнальном канале, характеристики которого регулируются изменением усиления усилителя.

Оптимизированный протокол геральдованной генерации позволяет создавать высокоточные не-гауссовы состояния, включая сжатые и фотонные состояния, из различных входных сигналов.

Несмотря на значительный прогресс в квантовой оптике, генерация неклассических состояний света с заданными характеристиками остается сложной задачей. В данной работе, посвященной ‘Generalized Heralded Generation of Non-Gaussian States Using an Optical Parametric Amplifier’, представлен обобщенный протокол геральдного оптического параметрического усилителя, способный эффективно генерировать широкий класс не-гауссовых состояний, включая сжатые состояния и суперпозиции чисел фотонов. Показано, что предложенная схема, используя как сжатый вакуум, так и малые амплитуды сжатых состояний, обеспечивает детерминированное создание высококачественных квантовых состояний из единой интегрированной установки. Открывает ли это путь к созданию масштабируемых квантовых вычислительных устройств и более эффективным протоколам квантовой коммуникации?

За пределами Гауссовых Состояний: Поиск Неклассического Света

Современные квантовые технологии, такие как квантовые вычисления и квантовая связь, требуют создания и управления квантовыми состояниями с беспрецедентной точностью. Однако, классическое описание, основанное на привычных понятиях энергии и импульса, часто оказывается недостаточным для адекватного представления этих состояний. В то время как классическая физика описывает системы через определенные значения параметров, квантовые системы могут находиться в суперпозиции состояний, что невозможно представить в рамках классической модели. Это приводит к тому, что предсказания, основанные на классическом подходе, расходятся с экспериментальными результатами, особенно при работе с запутанными фотонами или другими неклассическими явлениями. Поэтому, для полноценной реализации потенциала квантовых технологий необходимо разрабатывать и использовать квантово-механические модели, учитывающие все особенности поведения квантовых систем, и применять методы, выходящие за рамки классического понимания.

Традиционные гауссовские состояния, несмотря на свою удобство в математическом описании и простоту генерации, оказываются недостаточными для реализации сложных протоколов квантовой обработки информации. В то время как гауссовские состояния хорошо подходят для базовых операций, таких как квантовая телепортация или сжатое состояние света, они не обладают необходимой гибкостью и сложностью для кодирования и обработки информации в более продвинутых схемах, требующих, например, нелинейных взаимодействий или кодирования информации в неклассических степенях свободы. Ограниченность гауссовских состояний проявляется в их неспособности эффективно представлять и манипулировать кубитами, необходимыми для реализации квантовых алгоритмов, и в их уязвимости к шумам и потерям информации. В связи с этим, для достижения значительного прогресса в области квантовых технологий, необходимо разрабатывать и использовать более сложные, неклассические состояния света, способные преодолеть эти ограничения и обеспечить надежную и эффективную квантовую обработку информации.

Для реализации всего потенциала квантовых устройств необходимо генерировать и характеризовать истинно неклассические, или негауссовы, состояния света. В то время как гауссовы состояния обеспечивают удобную отправную точку для многих квантовых протоколов, они недостаточно сложны для поддержки универсальных квантовых вычислений и продвинутой квантовой криптографии. Негауссовы состояния, характеризующиеся неклассическими корреляциями и распределениями вероятностей, позволяют реализовать операции, недоступные для гауссовых состояний, например, создание запутанных состояний более высокого порядка и реализацию квантовых алгоритмов, требующих нетривиальной фазовой информации. Разработка надежных методов генерации и точной характеризации этих состояний, включая использование таких инструментов как гомодинное детектирование и квантовая томография состояний, является ключевой задачей для дальнейшего развития квантовых технологий и создания более мощных и функциональных квантовых устройств. Например, использование сжатого света и нелинейных оптических процессов позволяет создавать негауссовы состояния, такие как состояния «кот Шрёдингера» и фотонные состояния NOON, которые являются перспективными кандидатами для квантовых сенсоров и квантовых коммуникаций.

Временная эволюция вигнеровских функций показывает, как различные уровни диссипации влияют на квантовые состояния, демонстрируя изменения для SV-входа (r=1.0, g=2.5), чётного (α=1.2, g=g₀) и нечётного (α=1.5, g=g₀) сверхпроводящих состояний при κt = 0.1, 0.5 и 1.0.
Временная эволюция вигнеровских функций показывает, как различные уровни диссипации влияют на квантовые состояния, демонстрируя изменения для SV-входа (r=1.0, g=2.5), чётного (α=1.2, g=g₀) и нечётного (α=1.5, g=g₀) сверхпроводящих состояний при κt = 0.1, 0.5 и 1.0.

Геральдированный ОПА: Путь к Негауссовости

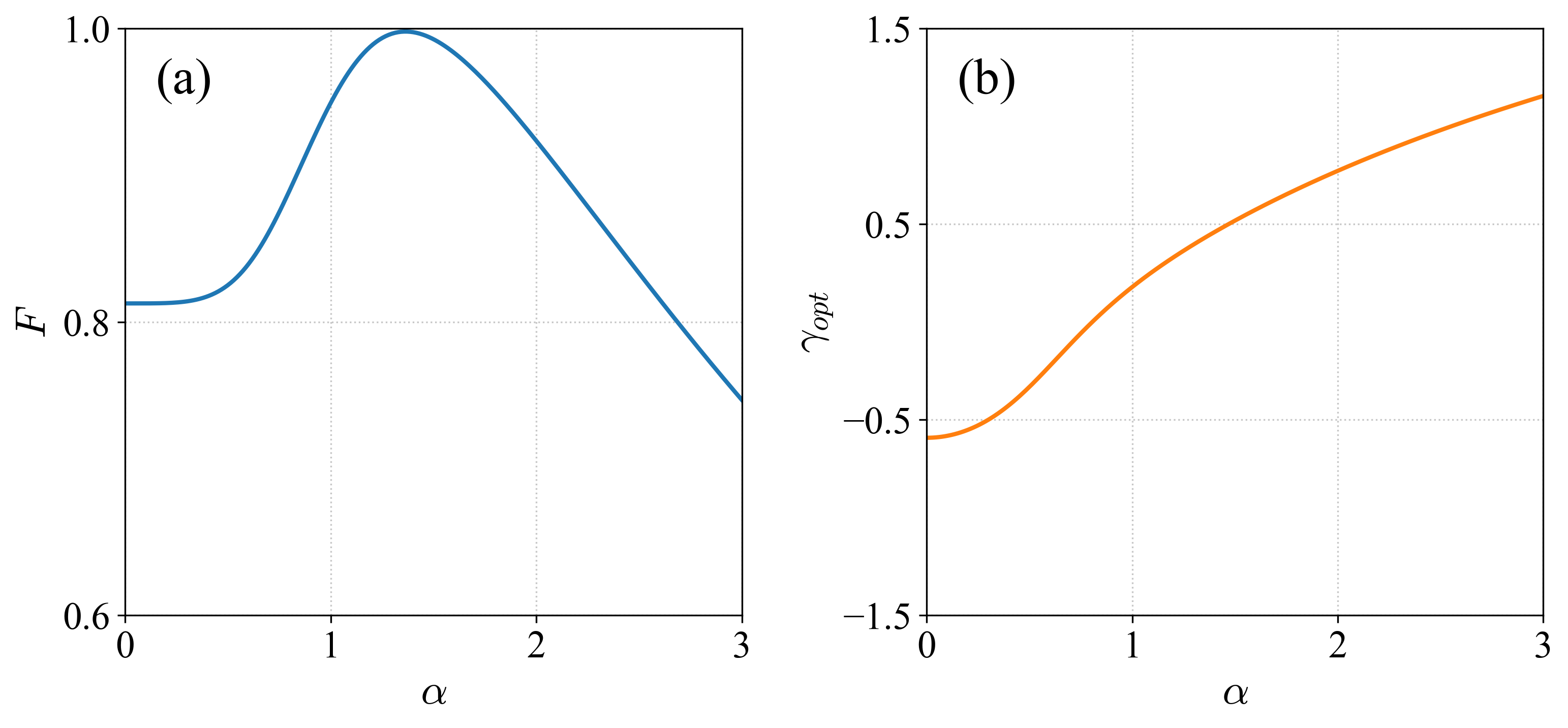
Протокол геральдированного оптического параметрического усилителя (OPA) представляет собой надежный метод генерации не-гауссовых состояний по запросу. В основе метода лежит использование сжатого вакуумного состояния в качестве входного сигнала и нелинейные свойства OPA для создания запутанности. Преимуществом данного подхода является возможность получения не-гауссовых состояний с заранее заданными характеристиками, что делает его востребованным в квантовых технологиях и экспериментах по квантовой оптике. В отличие от методов, основанных на прямом измерении квантовых характеристик, геральдированный OPA позволяет селективно генерировать определенные типы не-гауссовых состояний, такие как сжатые кошачьи состояния, с высокой точностью.

В основе метода создания неклассических состояний света лежит использование сжатого вакуумного состояния в качестве входного сигнала для оптического параметрического усилителя (OPA). Нелинейные свойства OPA, проявляющиеся в процессе параметрического рассеяния, приводят к возникновению корреляций между фотонами, что и является основой для создания запутанности. Входящий сжатый вакуум, характеризующийся уменьшением квантовых флуктуаций в одной из квадратур, подвергается взаимодействию в нелинейном кристалле OPA, генерируя пары коррелированных фотонов — сигнальный и холостой. Именно эта корреляция, возникающая за счет нелинейного взаимодействия, позволяет формировать запутанные состояния, необходимые для генерации неклассического света.

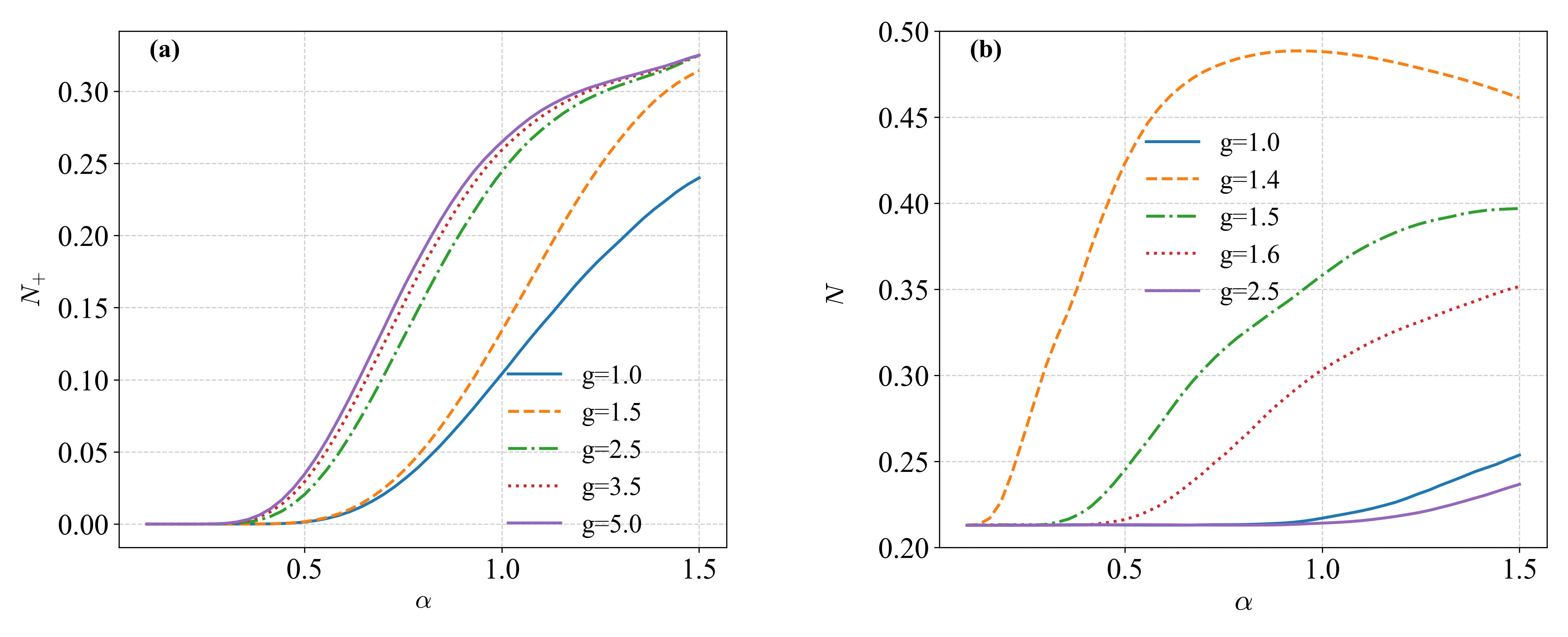
Протокол использования предвестника (heralded) позволяет спроецировать выходное состояние в требуемую не-гауссову форму, например, в сжатое кошачье состояние. Обнаружение фотона-предвестника служит триггером для реализации этой проекции, обеспечивая получение состояний с высокой степенью достоверности. Экспериментально достигнутые значения когерентной амплитуды для таких состояний составляют приблизительно $α≈1.4$, что подтверждает эффективность данного подхода для генерации сложных квантовых состояний.

Оптимальная точность воспроизведения целевого сжатого состояния даже волновой функции достигается при определенном значении параметра сжатия, при фиксированном параметре сжатия начального состояния.
Оптимальная точность воспроизведения целевого сжатого состояния даже волновой функции достигается при определенном значении параметра сжатия, при фиксированном параметре сжатия начального состояния.

Характеризация и Подтверждение Не-Классичности

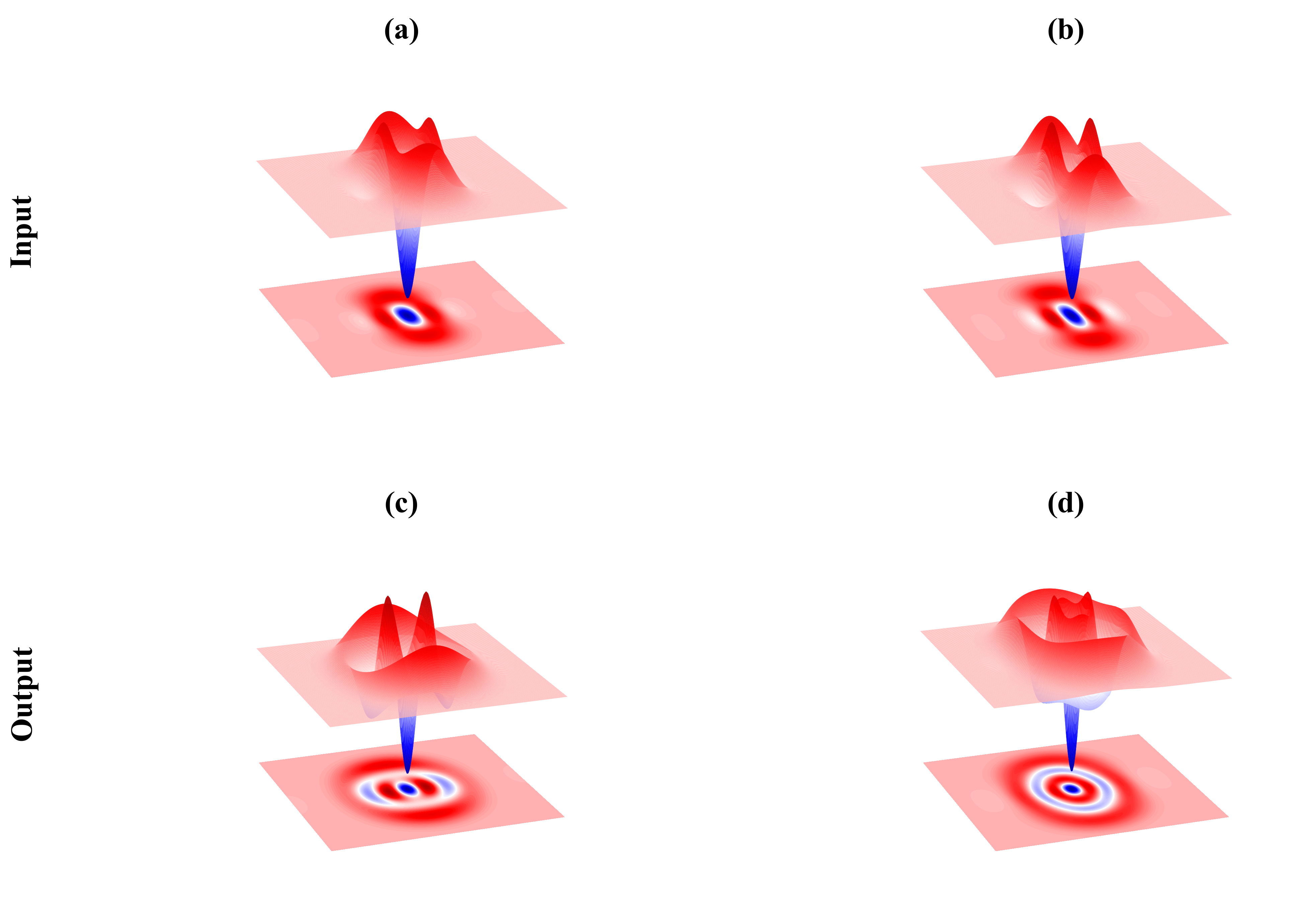
Функция Вигнера представляет собой мощный инструмент для визуализации и характеризации квантовых состояний, включая не-гауссовы. Она позволяет отобразить квантовое состояние в фазовом пространстве, подобно классической функции распределения вероятностей. В отличие от классических функций, функция Вигнера может принимать отрицательные значения, что является прямым признаком неклассичности состояния. Отрицательные значения свидетельствуют о наличии квантовой интерференции и корреляций, отсутствующих в классической механике. Анализ формы и значений функции Вигнера позволяет определить различные характеристики квантового состояния, такие как его степень запутанности и неклассичности, а также оценить его близость к другим квантовым состояниям. Это делает функцию Вигнера незаменимым инструментом в квантовой оптике и квантовой информатике для анализа и верификации создаваемых квантовых состояний, включая сложные не-гауссовы состояния, используемые в квантовых технологиях.

Отрицательные значения функции Вигнера являются прямым индикатором неклассичности квантового состояния. В классической механике функция Вигнера всегда неотрицательна, поскольку представляет собой распределение вероятностей. Обнаружение отрицательных значений указывает на то, что состояние не может быть описано классической фазовой пространственной структурой и демонстрирует квантовые корреляции, такие как запутанность или сжатие. Таким образом, отрицательность функции Вигнера служит надежным критерием для подтверждения создания неклассических состояний, таких как суперпозиции чисел фотонов или сжатые состояния, и является важным инструментом для характеризации квантовых ресурсов.

В ходе данной работы продемонстрирована генерация суперпозиций чисел фотонов высокой точности, достигающих значений верности более 0.99 для состояний, таких как $|0\rangle — 1.4|2\rangle$ и сжатых трёхфотонных состояний. Высокая верность полученных состояний подтверждается экспериментальными данными и свидетельствует о возможности создания квантовых состояний с превосходящими классические аналоги характеристики. Достижение таких значений верности критически важно для реализации протоколов квантовой информации и квантовых вычислений, требующих стабильных и хорошо определенных квантовых состояний.

Объем отрицательной Вигнера зависит от амплитуды когерентного состояния и изменяется в зависимости от коэффициента усиления.
Объем отрицательной Вигнера зависит от амплитуды когерентного состояния и изменяется в зависимости от коэффициента усиления.

Борьба с Декогеренцией и Путь к Масштабируемым Квантовым Системам

Потеря фотонов является ключевым фактором, вызывающим декогеренцию — процесс, в результате которого квантовые состояния теряют свою неклассичность с течением времени. Этот эффект обусловлен тем, что информация о квантовом состоянии, закодированная в фотонах, необратимо рассеивается при их потере. Декогеренция представляет собой серьезное препятствие для создания стабильных и масштабируемых квантовых систем, поскольку она приводит к разрушению квантовой суперпозиции и запутанности — явлений, необходимых для квантовых вычислений и коммуникаций. Чем выше скорость потери фотонов, тем быстрее происходит декогеренция и тем сложнее поддерживать когерентность квантового состояния. Поэтому минимизация потерь фотонов является критически важной задачей в разработке практических квантовых технологий, и исследования направлены на создание материалов и архитектур, способных эффективно удерживать и направлять фотоны, тем самым продлевая время жизни квантовых состояний и повышая надежность квантовых операций.

Уравнение Линдблада представляет собой ключевой теоретический инструмент для описания процессов декогеренции, возникающих из-за потери фотонов и других факторов, влияющих на квантовые состояния. Данное уравнение позволяет математически моделировать эволюцию квантовой системы с учетом нежелательных взаимодействий с окружающей средой, приводящих к разрушению квантовой когерентности. Оно описывает, как плотность квантового состояния изменяется во времени под воздействием различных операторов, представляющих процессы диссипации энергии и обмена информацией с внешним миром. Применение уравнения Линдблада позволяет предсказывать скорость декогеренции и разрабатывать стратегии для ее минимизации, что критически важно для создания стабильных и масштабируемых квантовых систем. Благодаря этому, уравнение является основой для анализа и оптимизации квантовых схем и протоколов, обеспечивая теоретическую базу для борьбы с основными источниками ошибок в квантовых технологиях.

Исследование демонстрирует достижение абсолютных скоростей генерации квантовых состояний в диапазоне от $10^5$ до $10^7$ в секунду, благодаря использованию лазерных источников с высокой частотой повторения. Вероятности успешной генерации, варьирующиеся от $10^{-4}$ до $10^{-2}$, сопоставимы с показателями других схем с использованием предвестников. Интеграция фотонных устройств с сверхпроводящими детекторами и применение передовых протоколов, таких как геральдский оптический параметрический усилитель (ОПА), открывают перспективный путь к созданию устойчивых и масштабируемых квантовых систем, способных решать сложные вычислительные задачи и обеспечивать безопасную передачу информации.

Сравнение вигнеровских функций входного нечетного СК-состояния с амплитудами α=1.2 и α=1.5 демонстрирует, как усиление амплитуды с коэффициентами g=1.5 и g=g₀ влияет на форму выходного сигнала.
Сравнение вигнеровских функций входного нечетного СК-состояния с амплитудами α=1.2 и α=1.5 демонстрирует, как усиление амплитуды с коэффициентами g=1.5 и g=g₀ влияет на форму выходного сигнала.

Исследование демонстрирует изящный подход к генерации неклассических состояний света, используя обобщенный протокол оптического параметрического усилителя. Этот метод позволяет создавать состояния с нетривиальной функцией Вигнера, что открывает возможности для продвинутых квантовых вычислений. В этой работе системы не стремятся к мгновенному результату, а скорее учатся адаптироваться к энтропии, извлекая полезные состояния из, казалось бы, случайных процессов. Как заметил Эрвин Шрёдингер: «Нельзя научиться плавать, не намочив ног». Подобно тому, как система постепенно учится «стареть достойно», так и данный протокол позволяет системе эволюционировать к желаемым квантовым состояниям, не подавляя случайность, а используя ее в своих целях.

Куда же дальше?

Представленная работа, демонстрируя обобщенный протокол генерации не-гауссовых состояний, лишь подчеркивает фундаментальную асимметрию между созданием и сохранением квантовых состояний. Создать состояние — не проблема, проблема — удержать его от неумолимого распада, от растворения в шуме окружающей среды. Потеря фотонов, как эрозия, постепенно разрушает хрупкую структуру, созданную столь тщательно.

Будущие исследования, вероятно, сосредоточатся не столько на усложнении схем генерации, сколько на разработке более эффективных методов коррекции ошибок и защиты квантовой когерентности. Аптайм, редкая фаза гармонии во времени, становится не просто технической характеристикой, но и философским вызовом. Интересно, сможет ли квантовая техника достичь состояния, когда время перестанет быть врагом, а станет союзником в сохранении информации.

Нельзя исключать и поиск альтернативных платформ, где квантовые состояния будут более устойчивы к воздействию времени. Возможно, истинный прогресс лежит не в борьбе с распадом, а в принятии его как неизбежной части квантовой реальности. И тогда, создание не-гауссовых состояний станет не столько технической задачей, сколько искусством управления энтропией.

Оригинал статьи: https://arxiv.org/pdf/2511.20946.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-28 14:52