Хаос под воздействием импульсов: как дальнодействие меняет правила игры

от

Автор: Денис Аветисян

Новое исследование показывает, как периодическое воздействие на систему взаимодействующих спинов приводит к переходу от защищенного поведения к хаотической тепловизации в зависимости от силы взаимодействия.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал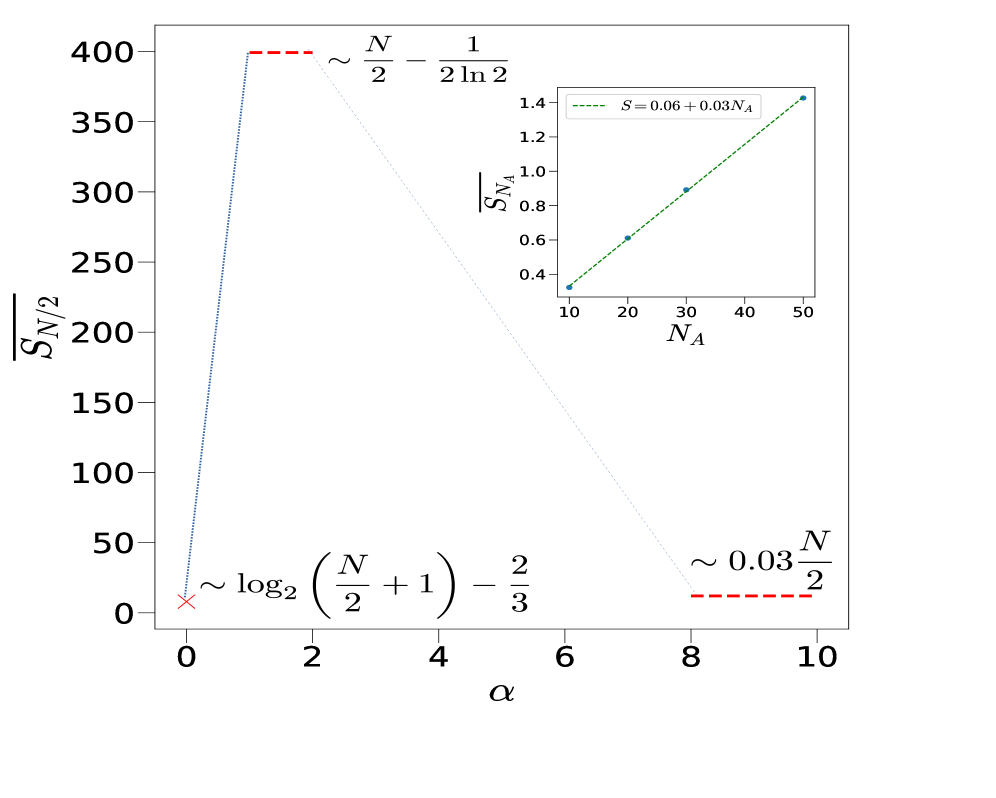
Для анализа энтропии $S_{N/2}$ при $N=800$ установлено, что при $\alpha=0$ (случайная перестановка в $N+1$-мерном пространстве) и $1 \leq \alpha \leq 2$ (значение Page в $2^N$-мерном гильбертовом пространстве) значения $S_{N/2}$ вычисляются полуаналитически для различных размеров подсистемы $N_A$, что позволяет определить зависимость энтропии от параметров системы.
Для анализа энтропии $S_{N/2}$ при $N=800$ установлено, что при $\alpha=0$ (случайная перестановка в $N+1$-мерном пространстве) и $1 \leq \alpha \leq 2$ (значение Page в $2^N$-мерном гильбертовом пространстве) значения $S_{N/2}$ вычисляются полуаналитически для различных размеров подсистемы $N_A$, что позволяет определить зависимость энтропии от параметров системы.

Работа посвящена исследованию тепловизации периодически возбуждаемой спиновой системы с дальнодействующим взаимодействием, демонстрирующей переход от симметрии к хаосу и интеграбельности.

Сложно предсказать поведение квантовых систем при наличии дальнодействующих взаимодействий и периодического воздействия. В данной работе, посвященной исследованию ‘Floquet thermalization by power-law induced permutation symmetry breaking’, мы изучаем влияние степенных законов затухания взаимодействий между спинами на динамику системы под воздействием периодического возмущения. Показано, что при изменении параметра, определяющего дальность взаимодействия, система демонстрирует переход от сохранения симметрии к тепловому равновесию, а затем к интегрируемости. Какие механизмы лежат в основе этого перехода и как их можно использовать для управления квантовыми системами?

За пределами равновесия: головоломка дальнодействующих взаимодействий

Традиционные модели, описывающие процесс установления теплового равновесия в многочастичных системах, зачастую исходят из предположения о взаимодействии частиц только на небольших расстояниях. Однако, данное упрощение оказывается неадекватным при рассмотрении широкого класса систем, где влияние одной частицы распространяется на значительные расстояния. В таких случаях, классические подходы не способны корректно предсказать динамику системы и ее переход к равновесному состоянию. Например, в квантовых спиновых системах или астрофизических плазмах, долгорадиусные взаимодействия играют определяющую роль в формировании коллективного поведения частиц, приводя к новым и неожиданным эффектам, которые невозможно объяснить в рамках стандартных моделей, предполагающих лишь локальные взаимодействия между частицами. Необходимость учета этих взаимодействий становится ключевой для адекватного описания поведения сложных систем и понимания их фундаментальных свойств.

Понимание дальнодействующих взаимодействий имеет решающее значение для точного описания динамики сложных систем, охватывающих широкий спектр областей науки. От квантовых спиновых систем, где корреляции между частицами могут простираться на значительные расстояния, до астрофизических плазм, где гравитационные и электромагнитные силы определяют поведение материи, дальнодействие играет фундаментальную роль. Традиционные модели, ориентированные на близкодействующие силы, зачастую оказываются неадекватными для описания таких систем, приводя к неверным прогнозам и неполному пониманию их свойств. Изучение этих взаимодействий позволяет создавать более реалистичные модели, способные предсказывать поведение сложных систем в различных условиях и раскрывать новые физические явления, например, формирование структур в плазме или возникновение необычных магнитных состояний в твердых телах.

Исследование демонстрирует, что спиновые системы с дальнодействующими взаимодействиями проявляют поведение, характеризующееся тепловым равновесием, которое можно регулировать посредством двух ключевых параметров: параметра дальности взаимодействия, обозначаемого как $α$, и периода внешнего воздействия, обозначаемого как $τ$. В частности, установлено, что изменение этих параметров оказывает существенное влияние на скорость и характер установления теплового равновесия в системе. Посредством численного моделирования показано, что при определенных значениях $α$ и $τ$ система способна быстро достигать теплового равновесия, в то время как при других значениях наблюдается более медленное и сложное поведение. Эти результаты подчеркивают важность учета дальнодействующих взаимодействий при описании динамики сложных систем и открывают новые возможности для управления их свойствами.

Периодические возмущения и формализм Флоке

Периодически возбуждаемые системы представляют собой эффективный инструмент для управления и исследования сложных динамических процессов, особенно в системах с дальнодействующими взаимодействиями. Воздействие периодической силы позволяет контролировать траектории движения частиц и изменять стабильность системы, что невозможно в статических условиях. Дальнодействие, подразумевающее взаимодействие частиц на больших расстояниях, усложняет анализ, однако периодическое возбуждение может использоваться для структурирования фазового пространства и подавления хаотического поведения, что позволяет исследовать и контролировать коллективные явления в таких системах. В частности, данный подход находит применение в изучении плазмы, спиновых систем и других коллективных явлений, где взаимодействие между элементами происходит на больших расстояниях и играет ключевую роль в формировании динамики.

Оператор Флоке, определяющий эволюцию системы в течение одного периода, представляет собой ключевой математический инструмент для анализа периодически управляемых систем. Он выражается как произведение унитарного оператора $U(T)$, описывающего эволюцию в течение периода $T$, и временного оператора $e^{-iHT}$, где $H$ — гамильтониан системы. Собственные значения оператора Флоке имеют вид $e^{-i\epsilon_n T}$, где $\epsilon_n$ — квазиэнергии системы. Анализ спектра оператора Флоке позволяет определить устойчивость и динамические свойства периодически управляемых систем, а также исследовать переход к хаотическому поведению. Этот подход позволяет рассматривать периодическое воздействие как эффективное изменение гамильтониана системы и упрощает анализ долгосрочной динамики.

Переход от анализа статического равновесия к исследованию отклика систем на внешние воздействия и возмущения позволяет изучать динамические режимы, возникающие при периодическом управлении. Традиционный анализ статического равновесия рассматривает состояние системы в отсутствие внешних воздействий или при их постоянстве. Однако, многие реальные системы подвержены периодическим изменениям параметров или внешним силам. Изучение отклика системы на такие воздействия требует использования методов, позволяющих учитывать временную зависимость, таких как формализм Флоке, который описывает эволюцию системы за один период, и позволяет анализировать устойчивость и характер динамики, возникающей при периодическом воздействии. Это необходимо для понимания и контроля сложных систем, особенно в контексте долгосрочных взаимодействий и нелинейной динамики.

Ударный волчок: парадигма термиализации

Модель “Ударного волчка” представляет собой хаотическую систему, подвергающуюся периодическим импульсам, и служит конкретным примером того, как дальнодействующие взаимодействия могут приводить к терминализации. В данной модели, частица движется в двухмерном пространстве, испытывая импульсы силы через определенные интервалы времени. В отличие от систем с локальными взаимодействиями, где энергия может сохраняться на длительных временных масштабах, в “Ударном волчке” импульсы приводят к эффективному перераспределению энергии между различными степенями свободы системы. Это перераспределение энергии, обусловленное дальнодействием, и является ключевым механизмом, приводящим к достижению теплового равновесия и характеризующим терминализацию системы, даже при отсутствии прямых тепловых контактов с внешней средой.

Динамика модели «Ударный волчок» демонстрирует устойчивое поведение, сохраняя признаки термиализации даже при наличии сильных взаимодействий между элементами системы. В отличие от многих других хаотических систем, где сильные взаимодействия приводят к локализации и нарушению термиализации, «Ударный волчок» сохраняет статистические свойства, характерные для теплового равновесия. Это проявляется в сохранении спектральных характеристик, соответствующих ансамблю случайных матриц, и указывает на эффективное распределение энергии по всем степеням свободы системы даже при значительной силе взаимодействий между частицами.

Анализ спектральных статистик подтверждает возникновение теплового поведения в модели «ударного волчка». В частности, вычисленное среднее отношение расстояний между уровнями ($⟨r⟩$) составляет 0.529 для промежуточных значений параметра $\alpha$. Это значение соответствует статистике Вигнера-Дисона, что указывает на хаотический характер системы и ее тенденцию к тепловому равновесию. Соответствие статистике Вигнера-Дисона является ключевым индикатором хаоса и подтверждает, что энергетические уровни системы демонстрируют характерные для хаотических систем корреляции.

Интегрируемость и границы термиализации

Модель «ударного Изинга», представляющая собой интегрируемое расширение классической модели «ударного волчка», демонстрирует поведение, существенно отличающееся от типичных хаотических систем. В отличие от систем, стремящихся к тепловому равновесию, данная модель не достигает полной термизации. Это означает, что энергия в системе не распределяется равномерно по всем степеням свободы, и корреляции между различными частями системы сохраняются даже после длительного времени. Исследования показывают, что наличие интегралов движения в модели «ударного Изинга» препятствует полной хаотизации и, следовательно, термодинамическому равновесию, подчеркивая фундаментальную роль неинтегрируемости в процессе достижения теплового состояния в физических системах. Данное отличие делает модель ценным инструментом для изучения границ применимости статистической физики и понимания механизмов, лежащих в основе теплового поведения сложных систем.

Исследования показывают, что способность системы достигать теплового равновесия напрямую связана с её неинтегрируемостью. Интегрируемые системы, обладающие достаточным количеством сохраняющихся величин, демонстрируют ограниченное тепловое поведение и не достигают полного теплового равновесия, в отличие от хаотичных, неинтегрируемых систем. Неинтегрируемость позволяет энергии равномерно распределяться по всем степеням свободы, что является необходимым условием для установления теплового равновесия. Отсутствие достаточного количества сохраняющихся величин в неинтегрируемых системах приводит к эффективному перемешиванию фазового пространства и, как следствие, к достижению теплового равновесия, в то время как интегрируемые системы остаются ограниченными в своем динамическом поведении и демонстрируют отклонения от теплового поведения.

В хаотическом режиме модели, эффективная размерность ($D_{eff}$) стремится к значению $2^{N-1}$ при умеренных значениях параметра $\alpha$. Этот феномен указывает на экспоненциальный рост числа степеней свободы, доступных системе, что затрудняет достижение теплового равновесия. При дальнейшем увеличении $\alpha$, отношение среднего расстояния между уровнями энергии (⟨r⟩) приближается к значению 0.386, характерному для пуассоновской статистики. Такой переход от госсевского распределения к пуассоновскому свидетельствует о потере способности системы к эффективному тепловому распределению энергии, демонстрируя, что даже в хаотических системах, полное тепловое равновесие не всегда гарантировано, а поведение может отклоняться от предсказаний классической статистической механики.

Эффективная сложность и пути к равновесию

Эффективная размерность, представляющая собой меру числа фактически занятых состояний в системе, играет ключевую роль в определении ее способности к тепловому равновесию. Вместо рассмотрения полного пространства состояний, которое может быть огромным и недоступным для анализа, данный показатель фокусируется на реально вовлеченных в динамику степенях свободы. Чем выше эффективная размерность, тем больше состояний участвует в тепловом обмене и, следовательно, тем быстрее система приближается к термодинамическому равновесию. Напротив, низкая эффективная размерность указывает на ограниченное число доступных состояний, что может приводить к медленной тепловизации или даже к возникновению неравновесных состояний. Таким образом, оценка эффективной размерности позволяет получить глубокое понимание поведения сложных систем и предсказать их эволюцию во времени, особенно в условиях, когда традиционные методы оказываются неэффективными.

Исследования показывают, что системы, характеризующиеся эффективной размерностью ($D_{eff}$) приблизительно равной $2^{(N-1)}$ в промежуточной стадии эволюции, демонстрируют более выраженное стремление к тепловому равновесию. Данное соотношение указывает на то, что при таком значении $D_{eff}$ число эффективно занятых состояний становится сопоставимо с общим числом возможных состояний, что способствует быстрому рассеянию энергии и установлению теплового баланса. По сути, система, находящаяся в указанном режиме, способна исследовать всё доступное фазовое пространство, что является необходимым условием для достижения теплового равновесия, в отличие от систем с существенно меньшей или большей эффективной размерностью, которые могут застревать в локальных минимумах или демонстрировать хаотическое поведение.

Исследование взаимодействия дальнодействующих сил, симметрий и эффективной размерности предоставляет целостную основу для понимания разнообразных путей к тепловому равновесию в сложных системах. В частности, анализ показывает, что при определенных условиях, таких как случайное распределение состояний, величина полного углового момента $⟨Jz^2⟩$ стремится к значению $N/4$, что указывает на специфическую структуру теплового состояния. Данный подход открывает новые горизонты для исследований в области статистической физики и позволяет глубже понять механизмы, управляющие эволюцией сложных систем к равновесию, а также прогнозировать их поведение в различных условиях. Рассмотрение этих факторов в совокупности способствует разработке более точных моделей и алгоритмов для анализа и управления сложными системами.

Исследование демонстрирует, что нарушение симметрии, вызванное степенными закономерностями, играет ключевую роль в переходе от защищённого симметрией поведения к тепловому равновесию. В данной работе показано, как взаимодействие дальнодействующих спинов под периодическим воздействием может приводить к интегральности системы. В связи с этим, вспоминается высказывание Эрвина Шрёдингера: «Я не уверен, что я понимаю, что такое фотон». Эта фраза отражает стремление к глубокому пониманию фундаментальных принципов, а представленное исследование, подобно попытке понять природу фотона, стремится раскрыть механизмы теплового равновесия в сложных квантовых системах, демонстрируя, что даже кажущиеся простыми системы могут таить в себе неожиданные сложности и требуют пристального внимания к деталям.

Что дальше?

Представленная работа, исследуя терминализацию систем с дальнодействующими взаимодействиями под периодическим воздействием, словно намекает на более глубокую структуру, скрытую за кажущимся хаосом. Переход от защищенного симметрией поведения к терминализации, а затем и к интегрируемости, заставляет задуматься: а не является ли сама терминализация не финальной стадией, а лишь точкой бифуркации, ведущей к новым, еще более упорядоченным состояниям? Возможно, «шум», возникающий в процессе терминализации, содержит в себе информацию о скрытых константах движения, которые пока остаются незамеченными.

Следующим шагом представляется расширение исследования за пределы модели Кик-Изинга. Какова роль различных типов дальнодействующих взаимодействий? Как изменяется картина терминализации в системах с более сложной топологией взаимодействий? И, что важнее, можно ли намеренно спроектировать систему, в которой терминализация является не разрушительным процессом, а инструментом для создания новых функциональных состояний? В конце концов, если баг — это не ошибка, а сигнал, то, возможно, и хаос терминализации является ключом к управлению сложными системами.

Необходимо также более внимательно изучить влияние флуктуаций и несовершенств на процесс терминализации. Реальные системы всегда далеки от идеальных, и понимание того, как эти отклонения влияют на динамику, имеет решающее значение для практического применения полученных результатов. И, конечно, не стоит забывать о возможности квантовых эффектов, которые могут существенно изменить картину терминализации в системах с сильными квантовыми флуктуациями.

Оригинал статьи: https://arxiv.org/pdf/2511.21284.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-29 21:13