Кваркониевые интерференции в магнитном поле: танец состояний

Автор: Денис Аветисян

Новое исследование раскрывает динамику переходов между состояниями очарованных кваркониев под воздействием изменяющегося магнитного поля, демонстрируя влияние скорости изменения и формы поля на их занятость.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Исследование демонстрирует интерференцию Ландау-Зенера-Штюккельберга (LZS) при треугольном импульсе магнитного поля, проявляющуюся в осцилляциях вероятностей диабатических переходов во времени и подтверждаемую аналитическим предсказанием LZS, что позволяет установить зависимость конечной вероятности перехода от длительности импульса.

Работа посвящена исследованию неадиабатической динамики очарованных кваркониев в переменных магнитных полях с использованием многоканальных гамильтонианов Ландау-Зенера-Штюкельберга-Майораны и анализом эффектов интерференции.

В условиях сильных магнитных полей спектр адронов демонстрирует избежание перекрестий, обусловленное смешением спиновых состояний. В настоящей работе, посвященной динамике ‘Landau-Zener-Stückelberg-Majorana dynamics of magnetized quarkonia’, исследуется влияние этих перекрестий на эволюцию очарованных кваркониев в переменных во времени магнитных полях. Показано, что неадиабатические переходы, включая переходы Ландау-Зенера и интерференцию Штуккельберга, существенно влияют на вероятности заселения состояний. Какие новые аспекты динамики адронов в экстремальных условиях можно выявить при дальнейшем изучении этих эффектов и их связи с экспериментальными данными?

Хармониум: Квантовый микроскоп для сильных взаимодействий

Хармониум, состоящий из очарованного кварка и антикварка, представляет собой уникальную систему для изучения квантовой хромодинамики — теории, описывающей сильные взаимодействия. Благодаря своей внутренней структуре и относительно большой массе, хароний особенно чувствителен к изменениям в вакуумной структуре и проявлениям непертурбативных эффектов, которые сложно исследовать другими методами. Изучение спектра и распада харония позволяет проверять предсказания теории в экстремальных условиях, а также уточнять параметры сильного взаимодействия. Фактически, хароний служит своего рода “микроскопом” для исследования фундаментальных свойств сильного взаимодействия, открывая путь к более глубокому пониманию структуры материи во Вселенной.

Изучение поведения чармония — системы, состоящей из очарованного кварка и антикварка — в присутствии внешних полей имеет первостепенное значение для проверки фундаментальных теорий сильных взаимодействий. Поскольку чармоний представляет собой чувствительный индикатор свойств кварк-глюонной плазмы и непертурбативных эффектов в квантовой хромодинамике, анализ его реакций на магнитные и электрические поля позволяет исследователям тестировать предсказания теоретических моделей за пределами возможностей стандартных методов возмущений. Наблюдение за изменениями в энергетических уровнях и спектральных характеристиках чармония в ответ на внешнее воздействие предоставляет уникальную возможность для уточнения параметров сильных взаимодействий и поиска отклонений от существующих теорий, что открывает новые горизонты в понимании фундаментальных законов природы.

Исследование поведения чармония под воздействием изменяющихся во времени магнитных полей открывает уникальные возможности для изучения переходов между его энергетическими уровнями. В рамках данной работы динамика этих переходов с высокой точностью описывается с помощью многоканальных гамильтонианов Ландау-Зенера. Этот подход позволяет детально анализировать вероятность переходов между различными состояниями чармония в зависимости от скорости изменения магнитного поля, что критически важно для проверки предсказаний квантовой хромодинамики. Использование $\mathcal{H}_{LZ}$ позволяет эффективно моделировать неадиабатические процессы, происходящие в системе, и выявлять ключевые параметры, определяющие стабильность и эволюцию чармония в сильных магнитных полях. Результаты подобных исследований вносят значительный вклад в понимание фундаментальных взаимодействий в мире адронов и позволяют проверить справедливость теоретических моделей, описывающих сильные взаимодействия.

Многоканальная модель Линдемана-Захарова (LZ) успешно воспроизводит спектр кварковой модели, включая дополнительные антипереходы и высоковозбужденные состояния, при увеличении числа каналов, что подтверждается хорошим соответствием между расчетными энергиями <span class="katex-eq" data-katex-display="false">\alpha_{i}</span>, <span class="katex-eq" data-katex-display="false">\delta_{i}</span> и <span class="katex-eq" data-katex-display="false">\Delta_{i,i+1}</span> (см. Таблицу 1) и экспериментальными данными. — Многоканальная модель Линдемана-Захарова (LZ) успешно воспроизводит спектр кварковой модели, включая дополнительные антипереходы и высоковозбужденные состояния, при увеличении числа каналов, что подтверждается хорошим соответствием между расчетными энергиями $\alpha_{i}$ , $\delta_{i}$ и $\Delta_{i,i+1}$ (см. Таблицу 1) и экспериментальными данными.

Неадиабатические переходы: Механизм Ландау-Зенера

Переход Ландау-Зенера представляет собой базовый механизм для описания неадиабатических переходов между квантовыми состояниями. В отличие от адиабатических процессов, где система остается в исходном состоянии при медленном изменении внешних параметров, неадиабатические переходы происходят, когда изменение параметров происходит достаточно быстро, чтобы вызвать переход в другое квантовое состояние. Вероятность такого перехода определяется соотношением между скоростью изменения внешнего воздействия и величиной энергетической щели между состояниями. Этот механизм находит применение в различных областях, включая физику конденсированного состояния, квантовую оптику и молекулярную динамику, для объяснения явлений, связанных с переходом между энергетическими уровнями под действием внешних возмущений.

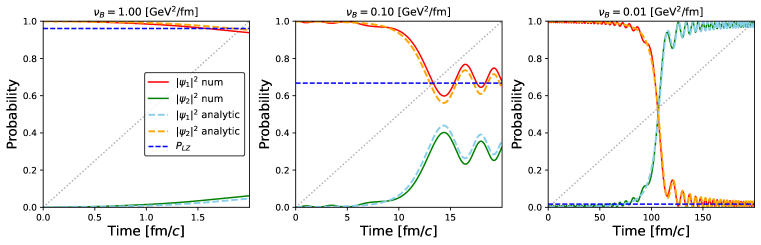
Вероятность ландау-зе́неровского перехода критически зависит от скорости изменения внешнего поля и величины энергетической щели между уровнями. Экспериментально это подтверждается при варьировании скорости изменения поля, когда наблюдаются характерные осцилляции в вероятности перехода. Более высокая скорость изменения поля подавляет переход, в то время как уменьшение скорости способствует ему. Величина энергетической щели Δ также играет ключевую роль: чем больше щель, тем менее вероятно неадиабатическое пересечение и, соответственно, переход. Наблюдаемые осцилляции обусловлены интерференцией между адиабатическим и неадиабатическим вкладами в волновой функции, что проявляется в периодическом изменении вероятности перехода в зависимости от параметров системы.

Ключевым элементом модели Ландау-Зенера является построение соответствующего гамильтониана, адекватно описывающего физику системы. Гамильтониан учитывает взаимодействие между квантовыми состояниями и внешним полем, определяя вероятность неадиабатических переходов. Для количественной оценки адиабатичности и предсказания вероятностей переходов используется параметр $λ = Δ²/|ν_{eff}|$ , где Δ — энергетическая щель между уровнями, а $ν_{eff}$ — эффективная скорость изменения внешнего поля. Значение λ определяет, насколько система остается в своем начальном состоянии при изменении поля: малые значения λ соответствуют адиабатическому режиму, а большие — неадиабатическому, приводящему к переходу между состояниями.

Численное решение уравнения Шрёдингера демонстрирует хорошее соответствие с аналитическим предсказанием Ландау-Зенера для различных скоростей изменения параметров, несмотря на небольшие расхождения, обусловленные различием в начальных условиях и отсутствием пред-переходных осцилляций в аналитических кривых.

Интерференция и избежание сближений: Точная настройка динамики

Переходы, избегающие сближения (avoided crossings), представляют собой ключевые особенности поверхности потенциальной энергии системы. Они возникают при наличии взаимодействия (coupling) между энергетическими уровнями, что приводит к отталкиванию этих уровней в точках, где они в противном случае пересеклись бы. Это отталкивание приводит к образованию зазора в энергетическом спектре и изменяет характер динамики системы, поскольку прямые переходы между уровнями становятся невозможными. Вместо этого, система эволюционирует, избегая сближения уровней, что оказывает существенное влияние на вероятности переходов и требует учета при моделировании динамических процессов. Величина зазора зависит от силы взаимодействия между уровнями и определяет скорость изменения состояний системы вблизи точек избежания сближения.

Пересечения энергетических уровней, известные как избежания пересечений, приводят к возникновению интерференции Штюкельберга. Этот эффект проявляется как модификация вероятностей переходов, рассчитываемых с использованием стандартного подхода Ландау-Зенера. В частности, интерференция Штюкельберга возникает из-за когерентного наложения волновых функций, описывающих различные пути перехода через избежание пересечений, что приводит к как увеличению, так и уменьшению вероятности перехода в зависимости от параметров системы и длительности импульса. Игнорирование этого явления может приводить к значительным погрешностям в предсказании динамики системы, особенно в случаях, когда система испытывает воздействие коротких импульсов или находится вблизи точек избежания пересечений.

Комбинирование эффектов Ландау-Зенера и интерференции Штюкельберга позволяет получить более точное описание динамики системы, особенно в случаях, когда скорость изменения параметров импульса сопоставима с характеристической частотой взаимодействия. Стандартный подход Ландау-Зенера предполагает асимптотическое поведение при быстром изменении параметров, игнорируя интерференционные эффекты, возникающие при более медленных изменениях. Учет интерференции Штюкельберга, обусловленной наложением волновых функций вблизи точек избежания пересечения потенциальных поверхностей, существенно влияет на вероятности переходов, особенно в отношении их зависимости от длительности импульса. Игнорирование этого влияния приводит к неточностям в моделировании динамики системы и прогнозировании вероятностей переходов, что особенно важно при анализе неадиабатических процессов.

В двухканальной модели, диабатические вероятности <span class="katex-eq" data-katex-display="false">P_{\rm dia}[J/\psi]</span> для начального состояния <span class="katex-eq" data-katex-display="false">\psi=(1,0)^{T}</span> демонстрируют интерференцию Штуккельберга и значительные изменения после второго прохождения, обусловленные малыми вариациями <span class="katex-eq" data-katex-display="false">\gamma_{P}</span>. — В двухканальной модели, диабатические вероятности $P_{\rm dia}[J/\psi]$ для начального состояния $\psi=(1,0)^{T}$ демонстрируют интерференцию Штуккельберга и значительные изменения после второго прохождения, обусловленные малыми вариациями $\gamma_{P}$ .

Влияние профиля поля: Управление квантовой эволюцией

Различные временные профили магнитного поля, включая линейные нарастания, гауссовы импульсы и экспоненциальные затухания, способны инициировать квантовые переходы в системе. Исследования показывают, что форма и продолжительность этих импульсов оказывают существенное влияние на вероятность перехода между энергетическими уровнями. Например, медленное линейное нарастание поля может способствовать адиабатическому переходу, в то время как короткий гауссовский импульс может вызвать неадиабатические переходы с высокой вероятностью. Изучение этих зависимостей позволяет точно управлять эволюцией квантовой системы и исследовать её свойства, открывая возможности для разработки новых квантовых технологий и манипулирования квантовыми состояниями. Спектральные характеристики переходов, вызванных различными профилями поля, могут быть использованы для диагностики и контроля над квантовыми процессами.

Форма профиля внешнего магнитного поля оказывает существенное влияние на вероятность квантовых переходов и, как следствие, на конечное состояние системы. Исследования показывают, что различные временные зависимости поля — линейные нарастания, гауссовы импульсы или экспоненциальные спады — приводят к разным результатам. Например, быстрые изменения поля могут способствовать неадиабатическим переходам, увеличивая вероятность перехода в другое квантовое состояние, в то время как медленные изменения способствуют сохранению исходного состояния. Таким образом, точный контроль над формой поля позволяет целенаправленно управлять эволюцией квантовой системы и исследовать её свойства с высокой точностью, открывая возможности для создания и манипулирования квантовыми состояниями.

Понимание зависимости эволюции системы от формы приложенного магнитного поля открывает возможности для точного управления ее состоянием и детального изучения квантовых свойств. Исследования показали, что манипулируя временными характеристиками поля — линейными нарастаниями, гауссовыми импульсами или экспоненциальным затуханием — можно целенаправленно изменять вероятности квантовых переходов. Полученные результаты подтверждают адекватность использования многоканальных гамильтонианов Ландау-Зенера для моделирования данной динамики, позволяя с высокой точностью предсказывать и контролировать эволюцию системы в различных условиях. Это, в свою очередь, способствует развитию новых методов квантового управления и исследованию фундаментальных аспектов квантовой механики.

На представленной схеме показаны избегаемые переходы в двухканальной модели при использовании различных профилей магнитного поля - линейных нарастаний, экспоненциального спада и гауссовых импульсов, причем первые два случая соответствуют однократному прохождению через точку избегания, а последний - двойному, что иллюстрируется стрелками, указывающими направление изменения поля во времени. — На представленной схеме показаны избегаемые переходы в двухканальной модели при использовании различных профилей магнитного поля — линейных нарастаний, экспоненциального спада и гауссовых импульсов, причем первые два случая соответствуют однократному прохождению через точку избегания, а последний — двойному, что иллюстрируется стрелками, указывающими направление изменения поля во времени.

Исследование динамики кваркониев в переменных магнитных полях, как представлено в данной работе, неизбежно сталкивается с проблемой скорости изменения параметров. Авторы, конструируя многоканальные гамильтонианы Ландау-Ценера, пытаются описать неадиабатические переходы, но всегда остается вопрос: насколько быстро можно менять поле, чтобы не получить хаос? Как справедливо заметил Поль Фейерабенд: «В науке нет единого метода, который бы гарантировал успех». В данном случае, стремление к точному математическому описанию сталкивается с практической необходимостью выбора оптимальной скорости изменения магнитного поля, влияющей на вероятность переходов и наблюдаемые интерференционные эффекты. Порой, элегантная теория уступает место необходимости простого, работающего решения, особенно когда речь идет о деплое экспериментальных результатов.

Что дальше?

Представленная работа, тщательно конструируя гамильтонианы Ландау-Зенера для кваркониев, неизбежно наталкивается на вопрос: а зачем это всё? Очевидно, что элегантность теоретического описания не гарантирует возможности воспроизвести наблюдаемые эффекты с требуемой точностью. В конце концов, если система стабильно падает, значит, она хотя бы последовательна. В дальнейшем необходимо учитывать не только профиль магнитного поля и скорость его изменения, но и неизбежные флуктуации среды, которые, как известно, всегда найдут способ разрушить самую изящную модель.

Интерференционные эффекты Штюккельберга, безусловно, любопытны, однако их практическая значимость остаётся туманной. Вместо того, чтобы увлеченно исследовать все возможные комбинации параметров, возможно, стоит сосредоточиться на более реалистичных сценариях, учитывающих взаимодействие кваркониев с окружающей плазмой. В конце концов, мы не пишем код — мы просто оставляем комментарии будущим археологам, которые попытаются понять, что вообще происходило.

«Cloud-native» кварконии, управляемые через API? Вероятно, это следующий этап. Однако, не стоит забывать, что все эти «революционные» технологии завтра станут техдолгом. В конечном счёте, предсказать, куда двинется поле исследований, бессмысленно. Продакшен всегда найдёт способ сломать элегантную теорию. И это, пожалуй, самое предсказуемое, что может произойти.

Оригинал статьи: https://arxiv.org/pdf/2512.24072.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-03 13:06