Кристаллы Времени и Пространства: Новая Геометрия Вселенной

от

Автор: Денис Аветисян

В статье представлена обобщенная математическая модель квазикристаллов, расширяющая ее границы с евклидова пространства на лоренцево, что открывает новые перспективы для понимания симметрии и структуры пространства-времени.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал
Представлены четыре варианта квазикристаллической структуры пространства-времени (1+1)(1+1)D, построенные на основе нечёткой самодвойственной решётки I3,1; каждый вариант демонстрирует различные свойства, обусловленные выбором весовой функции: варианты в верхнем ряду используют гауссово взвешивание с различной шириной окна, а варианты в нижнем ряду характеризуются масштабно-инвариантным поведением с разными значениями параметра k (1.01 и 0.25), при этом только k=1.01 обеспечивает конечность массы в ограниченной области и удовлетворяет критерию для получения ограниченной трансляцией меры, в то время как для визуализации в нижних панелях амплитуда пиков ограничена значением 10−6, чтобы избежать плотного заполнения плоскости незначительными коэффициентами.
Представлены четыре варианта квазикристаллической структуры пространства-времени (1+1)(1+1)D, построенные на основе нечёткой самодвойственной решётки I3,1; каждый вариант демонстрирует различные свойства, обусловленные выбором весовой функции: варианты в верхнем ряду используют гауссово взвешивание с различной шириной окна, а варианты в нижнем ряду характеризуются масштабно-инвариантным поведением с разными значениями параметра k (1.01 и 0.25), при этом только k=1.01 обеспечивает конечность массы в ограниченной области и удовлетворяет критерию для получения ограниченной трансляцией меры, в то время как для визуализации в нижних панелях амплитуда пиков ограничена значением 10−6, чтобы избежать плотного заполнения плоскости незначительными коэффициентами.

Исследование обобщает схему ‘вырезания и проектирования’ на лоренцево пространство для построения квазикристаллических структур и анализа их потенциальных физических свойств.

Несмотря на успехи современной физики, фундаментальные константы природы и иерархия масштабов остаются загадкой. В статье ‘Spacetime Quasicrystals’ предложен новый математический подход, обобщающий структуру квазикристаллов из евклидова пространства на пространство Минковского. Впервые построены примеры лоренц-квазикристаллов, демонстрирующие апериодичность и некристаллографическую симметрию в контексте пространства-времени. Может ли подобная структура, встраивающая нашу Вселенную в более симметричный многомерный тор, пролить свет на связь между планковской, вакуумной и электрослабой шкалами?

Порядок из Хаоса: Введение в Апериодические Структуры

Традиционная кристаллография, на протяжении десятилетий определявшая понимание упорядоченности в твердых телах, базируется на концепции трансляционной симметрии, реализуемой посредством кристаллических решеток. Это означает, что структура повторяется в пространстве с определенным периодом, что позволяет описывать ее небольшим набором параметров. Однако такое ограничение, хотя и эффективно для описания большинства известных материалов, оказалось недостаточным для понимания структур, демонстрирующих дальнодействующий порядок, не подчиняющийся периодическому повторению. Предположение о необходимости периодичности, глубоко укоренившееся в кристаллографии, долгое время препятствовало признанию и изучению материалов, чья упорядоченность выходит за рамки привычных латтисных структур, что потребовало пересмотра фундаментальных принципов и разработки новых методов анализа.

Квазикристаллы представляют собой уникальные материалы, бросающие вызов устоявшимся представлениям о кристаллической структуре. В отличие от традиционных кристаллов, обладающих периодическим узором, повторяющимся в пространстве, квазикристаллы демонстрируют дальний порядок, но лишены трансляционной симметрии. Этот феномен требует применения новых математических инструментов, таких как апериодические мозаики, в частности, укладки Пенроуза, для описания их сложной структуры. Вместо привычных решеток, квазикристаллы характеризуются узорами, которые упорядочены на больших расстояниях, но никогда не повторяются точно. a_{n+1} = a_n + (-1)^n — пример математического описания подобного непериодического поведения. Исследование квазикристаллов не только расширяет границы материаловедения, но и стимулирует развитие новых областей математики, позволяя глубже понять принципы организации материи.

Исследование апериодических структур, таких как квазикристаллы, требует отказа от традиционных методов кристаллографии, основанных на понятии трансляционной симметрии. Классические подходы, использующие решетки и группы симметрии, оказываются недостаточными для описания упорядоченности, не основанной на регулярном повторении. Вместо этого, необходимо применять новые математические инструменты, включая концепции многомерных решеток отсечения и икосаэдрической группы, для анализа дифракционных картин и определения симметрии апериодических материалов. Это приводит к переосмыслению самого понятия симметрии, открывая возможности для изучения новых видов упорядоченности и разработки материалов с уникальными свойствами, которые невозможно получить с помощью традиционных кристаллических структур.

Схема cut-and-project (sC&P) позволяет получить эвклидово квазикристаллическое покрытие с 8-кратной симметрией, как демонстрирует соответствие между патчем тайлинга Аммана-Бекера, его преобразованием Фурье и самодвойственным вариантом этого квазикристалла, где размер кругов отражает амплитуду дельта-функции, а цвет указывает на знак амплитуды.
Схема cut-and-project (sC&P) позволяет получить эвклидово квазикристаллическое покрытие с 8-кратной симметрией, как демонстрирует соответствие между патчем тайлинга Аммана-Бекера, его преобразованием Фурье и самодвойственным вариантом этого квазикристалла, где размер кругов отражает амплитуду дельта-функции, а цвет указывает на знак амплитуды.

Конструирование Апериодических Структур: Схема «Вырезание и Проецирование»

Схема «Вырезание и Проектирование» (Cut and Project) представляет собой эффективный метод генерации квазикристаллических структур, основанный на математическом построении апериодических узоров. В основе метода лежит проецирование многомерной структуры на пространство меньшей размерности, что позволяет создавать узоры с долгосрочным порядком, не обладающие трансляционной симметрией, характерной для классических кристаллов. Этот подход позволяет получать структуры, демонстрирующие порядок, отличный от периодического, и часто характеризующиеся определенными симметриями, такими как вращательная симметрия порядка, отличного от 1, 2, 3, 4 или 6. Геометрические свойства исходной многомерной структуры и способ проецирования определяют характеристики получаемой квазикристаллической структуры, включая ее симметрии и апериодичность.

Схема «вырезания и проецирования» (Cut and Project Scheme) основывается на использовании многомерных пространств для генерации апериодических структур с дальним порядком. Идея заключается в определении многомерной решетки, после чего происходит ее проекция на пространство меньшей размерности (обычно двумерное или трехмерное) с использованием определенного набора правил. Выбор многомерной решетки и правил проецирования определяет структуру полученного апериодического узора. Дальний порядок в структуре возникает благодаря определенной симметрии многомерной решетки и способу ее проецирования, что позволяет получить узоры, лишенные трансляционной симметрии, но сохраняющие определенные типы симметрии, характерные для квазикристаллов.

Схема симметричного отсечения и проецирования (Cut and Project Scheme, C&P) усовершенствует базовый метод, тесно интегрируя квазипериодичность, ориентационную симметрию и дискретную масштабную симметрию в процесс построения структур. В отличие от простых схем C&P, симметричный подход обеспечивает одновременное соблюдение этих трех ключевых свойств, что приводит к образованию апериодических структур с долгоrange упорядоченностью и предсказуемыми симметриями. Это достигается за счет выбора специфических параметров для отсечения и проецирования в higher-dimensional пространстве, гарантирующих, что результирующая структура обладает всеми требуемыми симметриями и квазипериодичностью, что критически важно для получения стабильных и предсказуемых квазикристаллических материалов. \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}

Figure 5:An illustration of the C&P scheme explained in Sec.III.1. Left panel: constructing the quasicrystalΛph𝐭,W\Lambda\_{{\rm ph}}^{{\bf t},W}. For each point𝐱∈Λ𝐭{\bf x}\in\Lambda^{{\bf t}}, if the “internal” point𝐱in=Πin​𝐱{\bf x}\_{\rm in}=\Pi\_{\rm in}{\bf x}lies inside the window𝒲{\cal W}, we include the “physical” point𝐱ph=Πph​𝐱{\bf x}\_{\rm ph}=\Pi\_{\rm ph}{\bf x}in the quasicrystalΛph𝐭,𝒲\Lambda\_{{\rm ph}}^{{\bf t},{\cal W}}(see Sec. Sec.III.1.1for details, included the weighted variant of the C&P scheme). Right panel: The corresponding Fourier transformΛ^ph𝐭,W\widehat{\Lambda}\_{{\rm ph}}^{{\bf t},W}is produced by a closely analogous C&P scheme: for each point𝐩∈Λ∗{\bf p}\in\Lambda\_{\ast}(the dual lattice), the Fourier transform includes a delta function located at the “physical” momentum𝐩ph=Πph​𝐩{\bf p}\_{\rm ph}=\Pi\_{\rm ph}{\bf p}, with a coefficient given byW^​(−𝐩i​n)\widehat{W}(-{\bf p}\_{in}), whereW^\widehat{W}is the Fourier transform of the “top-hat” or “indicator” function in the shape of the window𝒲{\cal W}, which is evaluated at the “internal” momentum𝐩in=Πin​𝐩{\bf p}\_{\rm in}=\Pi\_{\rm in}{\bf p}. As a display convention, one can represent the “height” of the delta function at𝐩ph{\bf p}\_{\rm ph}by a circular disk centered at𝐩ph{\bf p}\_{\rm ph}, with area proportional to the coefficientW^​(−𝐩in)\widehat{W}(-{\bf p}\_{\rm in}), as indicated by the red circles in the right panel.
Figure 5:An illustration of the C&P scheme explained in Sec.III.1. Left panel: constructing the quasicrystalΛph𝐭,W\Lambda\_{{\rm ph}}^{{\bf t},W}. For each point𝐱∈Λ𝐭{\bf x}\in\Lambda^{{\bf t}}, if the “internal” point𝐱in=Πin​𝐱{\bf x}\_{\rm in}=\Pi\_{\rm in}{\bf x}lies inside the window𝒲{\cal W}, we include the “physical” point𝐱ph=Πph​𝐱{\bf x}\_{\rm ph}=\Pi\_{\rm ph}{\bf x}in the quasicrystalΛph𝐭,𝒲\Lambda\_{{\rm ph}}^{{\bf t},{\cal W}}(see Sec. Sec.III.1.1for details, included the weighted variant of the C&P scheme). Right panel: The corresponding Fourier transformΛ^ph𝐭,W\widehat{\Lambda}\_{{\rm ph}}^{{\bf t},W}is produced by a closely analogous C&P scheme: for each point𝐩∈Λ∗{\bf p}\in\Lambda\_{\ast}(the dual lattice), the Fourier transform includes a delta function located at the “physical” momentum𝐩ph=Πph​𝐩{\bf p}\_{\rm ph}=\Pi\_{\rm ph}{\bf p}, with a coefficient given byW^​(−𝐩i​n)\widehat{W}(-{\bf p}\_{in}), whereW^\widehat{W}is the Fourier transform of the “top-hat” or “indicator” function in the shape of the window𝒲{\cal W}, which is evaluated at the “internal” momentum𝐩in=Πin​𝐩{\bf p}\_{\rm in}=\Pi\_{\rm in}{\bf p}. As a display convention, one can represent the “height” of the delta function at𝐩ph{\bf p}\_{\rm ph}by a circular disk centered at𝐩ph{\bf p}\_{\rm ph}, with area proportional to the coefficientW^​(−𝐩in)\widehat{W}(-{\bf p}\_{\rm in}), as indicated by the red circles in the right panel.

Обобщение на Пространство-Время: Квазикристаллы в Лоренцевой Геометрии

Пространственно-временные квазикристаллы формируются посредством применения схемы «Вырезание и Проецирование» (Cut and Project) в рамках геометрии пространства Минковского (Лоренцево пространство). Данный подход предполагает построение квазикристаллической структуры путем проецирования дискретного набора точек из ℝ^{n+1} на ℝ^n с использованием специального набора правил, адаптированных к свойствам метрики Лоренца. В отличие от классической схемы C&P, применяемой в евклидовом пространстве, версия для пространства Минковского учитывает различие между временными и пространственными координатами, что приводит к возникновению новых типов квазикристаллических структур, обладающих специфическими свойствами, обусловленными релятивистской геометрией.

Конструирование квазикристаллов в пространстве Минковского, или, более общо, в пространстве Лоренца, принципиально зависит от специфических свойств метрики Лоренца. В отличие от евклидова пространства, где расстояния определяются положительно определенной метрикой, пространство Лоренца характеризуется метрикой, допускающей отрицательные значения, что приводит к появлению светоподобных и пространственноподобных интервалов. Именно эта неевклидова геометрия, включающая понятие интервала ds^2 = -c^2dt^2 + dx^2 + dy^2 + dz^2, определяет допустимые векторы в пространстве, используемые в схеме «Вырезание и Проецирование» (Cut and Project). Изменение метрики напрямую влияет на выбор базиса и, следовательно, на структуру результирующего квазикристаллического узора, отличая его от аналогичных структур в евклидовом пространстве. Таким образом, свойства пространства Лоренца являются основополагающими для создания и понимания квазикристаллов, существующих в этой геометрии.

Схема «Вырезание и Проецирование» (Cut and Project — C&P) в контексте пространства Минковского предоставляет конкретный метод генерации пространственно-временных квазикристаллов, основываясь на принципах оригинальной схемы C&P. Данная схема адаптирует математический формализм, используемый для создания обычных квазикристаллов, к случаю пространственно-временных структур. Ключевым этапом является определение подходящего «реального» пространства и «фонового» пространства, а также выбор проекции, позволяющей получить апериодическую, но упорядоченную структуру в пространстве Минковского R^{1,3}. В отличие от традиционной схемы C&P, работающей в R^n, пространственно-временная схема учитывает сигнатуру метрики Минковского, что влияет на свойства результирующей структуры и ее дифракционную картину.

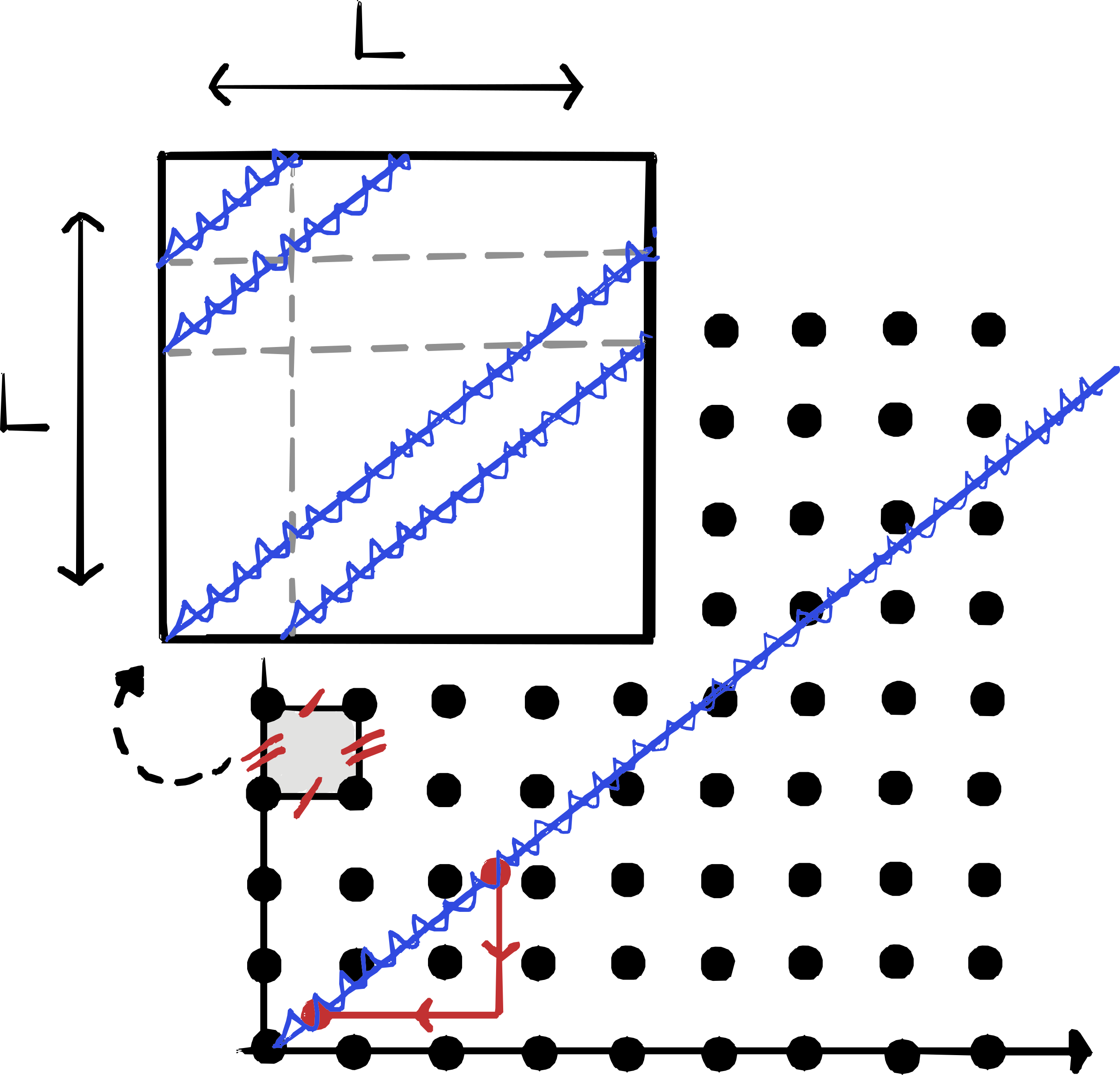
Квантовые флуктуации приводят к тому, что траектория, изначально бесконечно тонкая, неизбежно соприкасается с точками в многомерной решетке, что приводит к самопересечению соответствующей кривой на торе.
Квантовые флуктуации приводят к тому, что траектория, изначально бесконечно тонкая, неизбежно соприкасается с точками в многомерной решетке, что приводит к самопересечению соответствующей кривой на торе.

За Пределами Математики: Физические Импликации и Спекуляции

Существование пространственно-временных квазикристаллов открывает захватывающие перспективы для обнаружения совершенно новых физических структур и явлений. В отличие от традиционных кристаллов, характеризующихся периодичностью, квазикристаллы демонстрируют упорядоченность без трансляционной симметрии, что предполагает возможность формирования экзотических структур в ткани пространства-времени. Эта концепция, хотя и пока гипотетическая, позволяет предположить, что гравитационные волны или даже сама геометрия пространства-времени могут проявлять непериодические, квазикристаллические паттерны. Исследование этих структур может привести к пересмотру представлений о фундаментальных свойствах гравитации и открыть новые пути для понимания Вселенной, возможно, даже указывая на существование ранее неизвестных форм материи или энергии, взаимодействующих с пространством-временем уникальным образом.

Предложенная математическая модель, описывающая кристаллы пространства-времени, открывает возможность исследовать потенциальные связи между абстрактными математическими объектами и реально существующими физическими структурами. Несмотря на то, что на текущем этапе исследования носят преимущественно спекулятивный характер, разработанный формализм позволяет выдвигать гипотезы о возможности существования новых, ранее неизвестных форм организации материи во Вселенной. Изучение свойств этих математических кристаллов, таких как их непериодичность и способность к долгопорядочности, может привести к пониманию фундаментальных принципов, лежащих в основе формирования сложных структур, от кристаллов до космологических образований. Подобный подход, соединяющий абстрактную математику и физическую реальность, представляет собой плодотворное направление для дальнейших исследований в области теоретической физики и материаловедения.

Настоящая работа, расширяя математический аппарат, пока не предлагает конкретных количественных предсказаний относительно физической реальности. Это означает, что, несмотря на теоретическую элегантность и возможность существования пространственно-временных квазикристаллов, требуется дальнейшее исследование для установления связи между математической моделью и наблюдаемыми физическими явлениями. Будущие исследования должны быть направлены на разработку методов, позволяющих вывести из обобщенной формализации конкретные, проверяемые предсказания о свойствах материи и структуре пространства-времени, что позволит перейти от чисто теоретических построений к экспериментальной верификации и пониманию потенциальных физических последствий данной математической концепции.

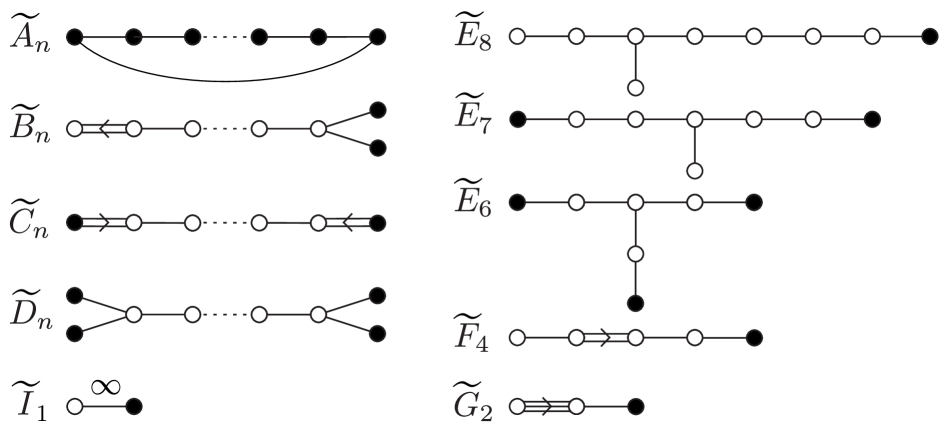
Диаграммы Коксетера-Динкина иллюстрируют структуру неразложимых групп Коксетера конечного/сферического и аффинного/плоскостного типов, при этом некристаллографические случаи выделены, а аффинные диаграммы получаются добавлением или удалением
Диаграммы Коксетера-Динкина иллюстрируют структуру неразложимых групп Коксетера конечного/сферического и аффинного/плоскостного типов, при этом некристаллографические случаи выделены, а аффинные диаграммы получаются добавлением или удалением «расширяющего корня» из соответствующих конечных диаграмм.

Математические Основы: Обеспечение Строгости и Согласованности

Глубокое понимание алгебраической теории чисел является основополагающим для анализа свойств квазикристаллов и их симметрий. Эта область математики предоставляет инструменты для изучения алгебраических чисел и их полей, что позволяет детально исследовать апериодические структуры, характерные для квазикристаллов. В частности, алгебраическая теория чисел позволяет описывать разрешимость уравнений, определяющих симметрии квазикристаллов, и устанавливать связи между их математическими свойствами и физическими характеристиками. \mathbb{Q}(\alpha) — расширение поля рациональных чисел, получаемое добавлением корня α многочлена, играет ключевую роль в описании этих структур. Исследование полей классов и их связей с дифракционными картинами квазикристаллов позволяет не только понять природу апериодичности, но и предсказывать новые материалы с уникальными свойствами, открывая перспективы для развития материаловедения и физики конденсированного состояния.

Группа Коксетера представляет собой мощный математический аппарат для описания симметрий, присущих апериодическим структурам, таким как квазикристаллы. В отличие от классических кристаллов, характеризующихся повторяющимися узорами и симметриями, квазикристаллы демонстрируют упорядоченность без трансляционной симметрии. Группы Коксетера позволяют формально описать эти сложные симметрии, определяемые набором отражений, и тем самым раскрыть фундаментальную структуру этих материалов. W = \langle r_1, ..., r_n \mid \text{отношения} \rangle — общее представление группы Коксетера, где r_i — отражения, а отношения определяют их взаимодействие. Использование этого подхода позволяет не только классифицировать различные типы квазикристаллов, но и предсказывать их физические свойства, открывая новые возможности для материаловедения и физики конденсированного состояния.

Дальнейшее математическое исследование представляется необходимым для полного раскрытия потенциала пространственно-временных квазикристаллов и их последствий для физики. Несмотря на значительный прогресс в понимании апериодических структур, многие аспекты их поведения, особенно в контексте гравитации и космологии, остаются неизученными. Углубленное изучение алгебраической теории чисел, групп Коксетера и связанных с ними математических инструментов позволит построить более точные модели и предсказания, касающиеся свойств этих экзотических структур. В частности, математики и физики совместно работают над разработкой новых методов анализа, способных описать взаимодействие квазикристаллов с гравитационными полями и предсказать возможные наблюдаемые эффекты, такие как аномалии в распространении гравитационных волн или модификации пространства-времени. \mathbb{Z} -структуры, лежащие в основе некоторых моделей, требуют тщательного анализа для выявления новых физических принципов, и дальнейшие математические разработки являются ключом к расшифровке этих сложных систем и раскрытию их потенциального влияния на наше понимание Вселенной.

Диаграммы Коксетера-Динкина иллюстрируют структуру неразложимых групп Коксетера конечного/сферического и аффинного/плоскостного типов, при этом некристаллографические случаи выделены, а аффинные диаграммы получаются добавлением или удалением
Диаграммы Коксетера-Динкина иллюстрируют структуру неразложимых групп Коксетера конечного/сферического и аффинного/плоскостного типов, при этом некристаллографические случаи выделены, а аффинные диаграммы получаются добавлением или удалением «расширяющего корня» из соответствующих конечных диаграмм.

Исследование демонстрирует, как из локальных правил, подобно формированию кораллового рифа, может возникать порядок в пространстве-времени. Авторы, обобщив математический аппарат квазикристаллов для лоренцева пространства-времени, показывают, что апериодичность и симметрия могут проявляться даже в таких экзотических структурах. Как отмечает Жан-Поль Сартр: «Существование предшествует сущности». Подобно тому, как квазикристаллическая структура возникает не из заранее заданной формы, а из определенных правил построения, так и порядок в пространстве-времени формируется не из изначально заданной структуры, а из локальных взаимодействий, подчеркивая роль ограничения как стимула для креативности и новых открытий.

Куда Ведет Кристаллическая Апериодичность?

Представленная работа, обобщив математический аппарат квазикристаллов на лоренцевское пространство-время, лишь приоткрывает дверь в область, где геометрия и симметрия переплетаются с кажущейся случайностью. Строительство примеров — это первый шаг, но истинный вызов заключается в поиске физических систем, которые могли бы воплотить предложенные структуры. Не стоит ожидать прямого соответствия наблюдаемым явлениям; скорее, необходимо рассматривать эти конструкции как новые элементы в языке описания сложных систем.

Очевидным ограничением является выбор конкретной схемы «вырезания и проецирования». Возможно, другие методы построения, акцентирующие иные аспекты апериодичности, откроют качественно новые классы структур. В конечном итоге, вопрос не в создании «идеального» квазикристалла в пространстве-времени, а в понимании того, как локальные флуктуации симметрии могут резонировать по всей сети, порождая макроскопические эффекты.

Порядок не нуждается в архитекторе. Предложенный подход подчеркивает, что кажущаяся сложность может возникать из простых локальных правил. Контроль над этими правилами — иллюзия, но влияние на их эволюцию — реальность. В дальнейшем, усилия должны быть направлены не на поиск «правильных» решений, а на исследование пространства возможностей, порождаемого этими правилами, и осознание того, что малые действия могут создавать колоссальные эффекты.

Оригинал статьи: https://arxiv.org/pdf/2601.07769.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-14 06:23