Автор: Денис Аветисян
Исследование взаимодействующих бозонов в искусственно созданных магнитных полях выявило необычные квантовые фазы и новый тип коллективного возбуждения.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал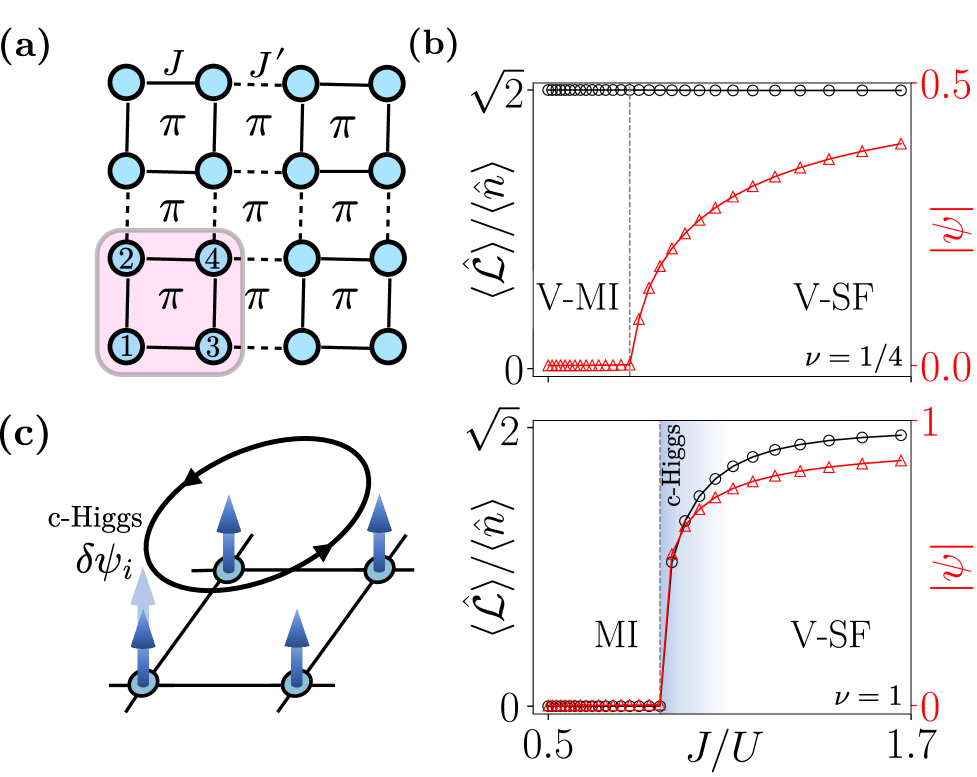
В работе исследуется появление хирального режима Хиггса в π-фрустрированных решетках, реализованных на димеризованных оптических решетках с нейтральными атомами.
Исследование сильнокоррелированных систем часто сталкивается с трудностями моделирования нетривиальных фаз материи. В работе «Emergent chiral Higgs mode in π-flux frustrated lattices» исследуется поведение взаимодействующих бозонов в димеризованной решетке ББХ с искусственно созданным магнитным потоком. Показано, что в данной системе реализуются различные квантовые фазы, включая вихревой сверхтекучий режим, и обнаружена хиральная мода Хиггса — коллективное возбуждение, возникающее при спонтанном нарушении симметрии времени. Открывает ли это путь к созданию новых экспериментально реализуемых платформ для изучения топологических состояний материи и хиральных квазичастиц?
Танцующие тени материи: Введение в модель BBH
Постоянный поиск новых квантовых фаз материи требует создания теоретических моделей, способных предсказывать и объяснять экзотическое поведение систем. В физике конденсированного состояния, традиционные подходы часто оказываются недостаточными для описания явлений, возникающих в сложных квантовых системах. Поэтому, исследователи активно разрабатывают новые математические конструкции и модели, стремясь к пониманию принципиально новых состояний материи, которые могут обладать необычными свойствами, такими как топологическая защита или нетривиальные корреляции. Эти модели служат отправной точкой для экспериментов и помогают направлять поиск материалов, в которых эти предсказанные фазы могут быть реализованы и изучены, открывая путь к новым технологиям и фундаментальным открытиям в области квантовой физики.
Модель Беналькасара-Берневига-Хьюза (BBH) представляет собой перспективную платформу для исследования экзотических квантовых фаз материи, основанную на димеризованной решетке с потоком π. В ее основе лежит бозонная система, что позволяет исследовать взаимодействие частиц и возникающие коллективные явления. Особенностью данной модели является ее способность поддерживать топологические состояния, характеризующиеся устойчивостью к локальным возмущениям и наличием защищенных граничных состояний. Димеризованная структура решетки и введение π-потока создают специфические условия для возникновения новых квантовых фаз, отличающихся от традиционных состояний материи. Изучение BBH модели позволяет углубить понимание фундаментальных принципов квантовой механики и открыть возможности для создания новых квантовых устройств.
Для глубокого понимания и верификации теоретических предсказаний, касающихся экзотических квантовых фаз, крайне важно проводить моделирование сложных систем. В последние годы значительный прогресс в области квантовых симуляций с нейтральными атомами открывает принципиально новые возможности для реализации и изучения таких моделей, как BBH. Используя контролируемые взаимодействия между атомами, заключенными в оптических ловушках, ученые могут создавать искусственные структуры, имитирующие поведение электронов в конденсированном веществе. Этот подход позволяет исследовать квантовые явления, которые трудно или невозможно изучить напрямую в материальных системах, и, таким образом, прокладывает путь к открытию новых квантовых материалов и технологий. Такие симуляции позволяют не только подтвердить теоретические расчеты, но и выявить неожиданные эффекты и фазы, расширяя наше понимание квантовой материи.
Раскрывая экзотические фазы с помощью теоретических инструментов
Приближение кластерного Гутцвиллера (Cluster Gutzwiller Approximation) представляет собой мощный метод среднеполевого приближения, используемый для анализа модели Буше-Буше (BBH) и предсказания ее квантовых фаз. Данный подход позволяет упростить сложную многочастичную задачу, аппроксимируя взаимодействие между частицами посредством усреднения по локальным конфигурациям. В рамках этого приближения, \langle \psi_i | O | \psi_j \rangle \approx \langle \psi_i | O \rangle \langle \psi_j | \rangle , где ψ — волновые функции, а O — оператор. Эффективность метода заключается в возможности исследовать фазовые диаграммы и предсказывать свойства квантовых систем, которые сложно рассчитать напрямую из-за экспоненциального роста размерности гильбертова пространства.
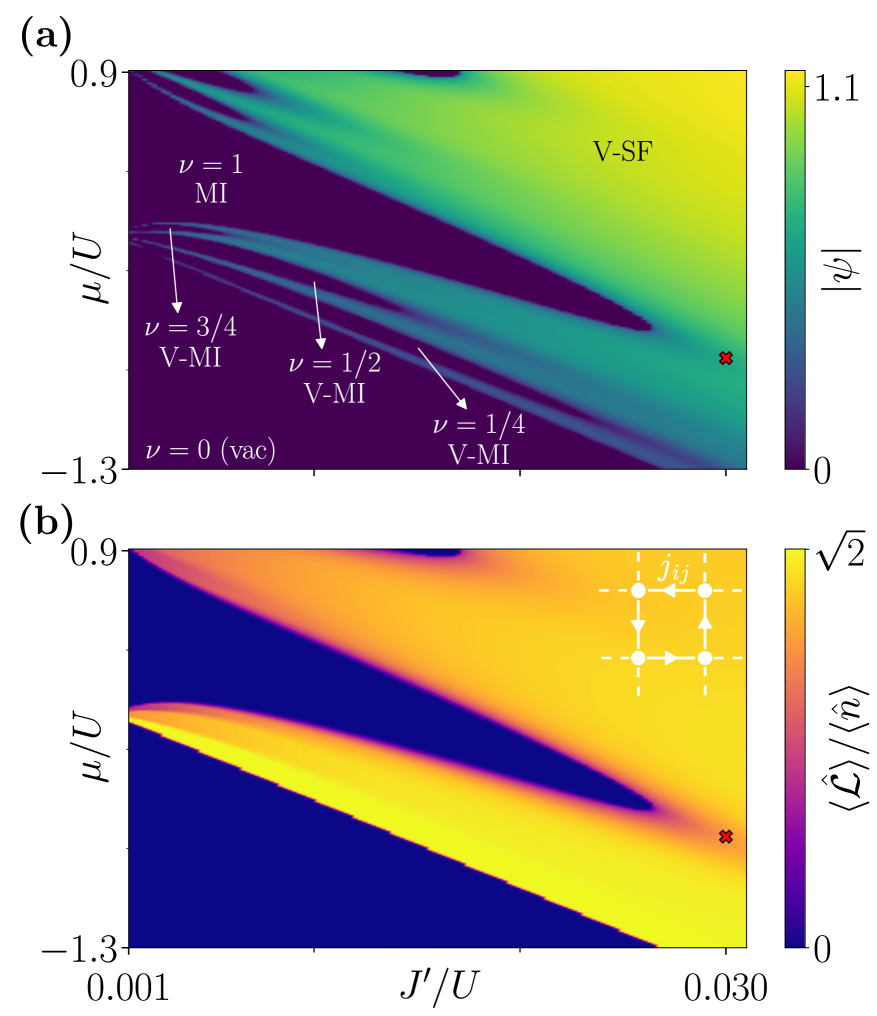
Теоретическое исследование модели BBH в рамках приближения Кластер-Гутцвиллера предсказывает возможность существования двух различных фаз вещества: вихревого сверхтекучего состояния и вихревого моттовского изолятора. Эти фазы возникают при определенных значениях фактора заполнения ν, в частности при ν = 1/4, ν = 1/2 и ν = 1. Различие между этими фазами обусловлено характером квантовых корреляций и способом организации электронных состояний в кристаллической решетке, что приводит к различным транспортным и магнитным свойствам.
В вихревых фазах, предсказанных для модели BBH, ключевым свойством является наличие циркулирующих токов — так называемых “петлевых токов” (Loop Currents) — внутри кристаллической решетки. Эти токи не являются нулевыми и имеют конечную величину, что принципиально отличает вихревые фазы от других состояний системы. Интенсивность и направление этих токов оказывают существенное влияние на наблюдаемые свойства фаз, включая их электрические и магнитные характеристики. Наличие этих токов подтверждается теоретическими расчетами в рамках приближения Кластер-Гутцвиллер и является определяющим фактором для классификации фаз как вихревых.
Вычислительная верификация и нарушение симметрии
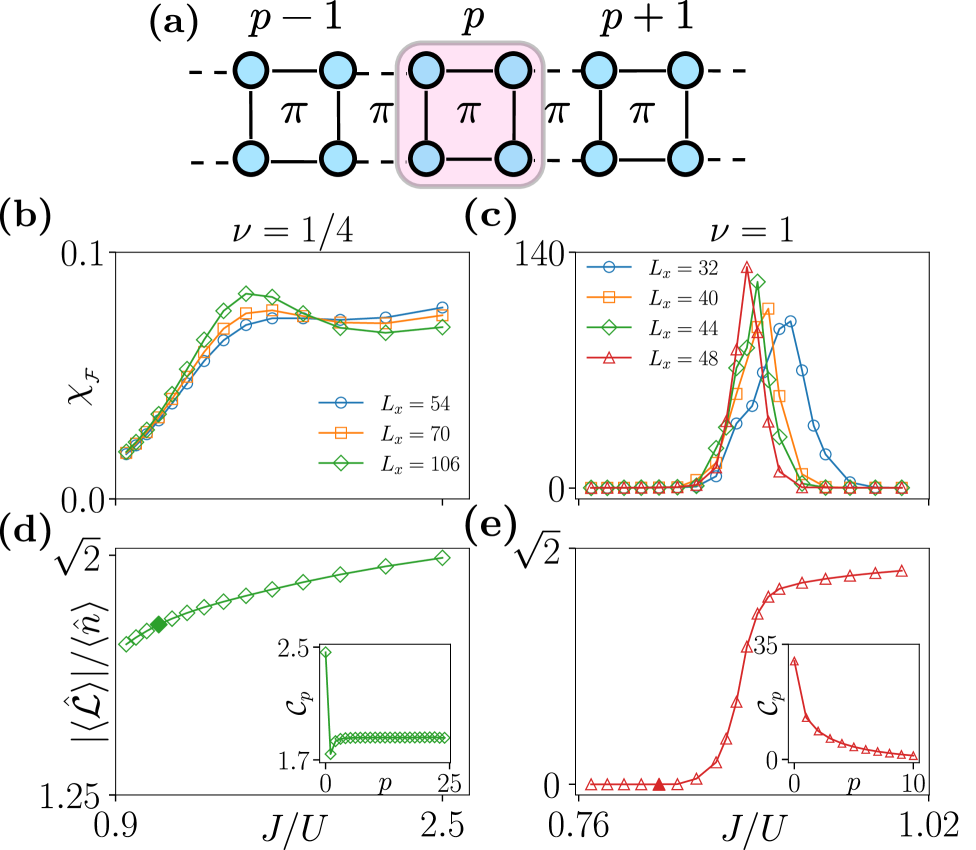
Для верификации результатов, полученных с помощью приближения Cluster Gutzwiller, применялась методика DMRG (Density Matrix Renormalization Group). Для достижения сходимости расчетов использовался максимальный размер связи \chi_{max} = 1600-{1800}. DMRG является дополнительным, более точным методом, позволяющим подтвердить фазовые диаграммы и энергетические характеристики системы, что необходимо для подтверждения надежности приближений, использованных на предыдущих этапах исследования.
Результаты численного моделирования с использованием метода DMRG подтверждают предсказанное существование различных фаз системы. В частности, установлено, что ключевую роль в стабилизации этих фаз играет фрустрация потока (Flux Frustration). Данный механизм, связанный с конкурирующими взаимодействиями между спинами и зарядами, приводит к формированию упорядоченных состояний, отличных от традиционных фаз, наблюдаемых в системах без фрустрации. Анализ полученных результатов показывает, что фрустрация потока является необходимым условием для возникновения и поддержания стабильности наблюдаемых фаз, что подтверждает теоретические предсказания.
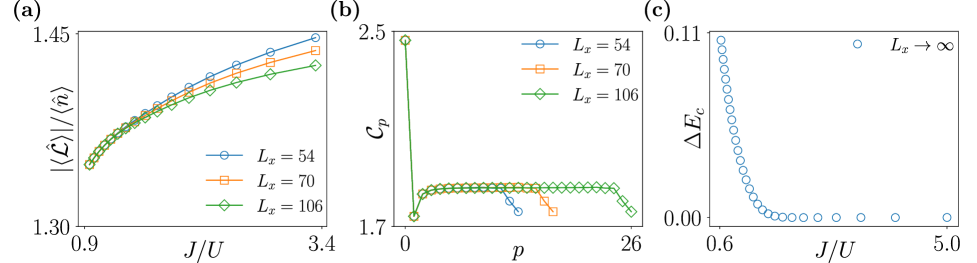
Результаты моделирования показывают, что фазы «вихревого сверхпроводника» и «вихревого моттовского изолятора» демонстрируют нарушение симметрии относительно обращения времени. Это указывает на возникновение нового типа квантового порядка, характеризующегося появлением конечного энергетического зазора Δ_{Ec} при заполнении ν = 1/2. Наличие этого зазора подтверждает, что моттовский изолятор является несжимаемым состоянием, что отличает его от обычных металлических состояний и указывает на сильную электрон-электронную корреляцию.
Топологические последствия и будущие направления
Модель Бхаттачарьи-Хаузера (BBH) демонстрирует возможность реализации так называемого высшего порядка топологического изолятора, что представляет собой качественно новый класс материалов, выходящий за рамки привычных топологических изоляторов. В отличие от последних, характеризующихся защищенными состояниями на грани раздела фаз, BBH-модель предсказывает возникновение подобных состояний не на поверхности, а на более низкоразмерных объектах — углах, шарнирах и других дефектах структуры. Это означает, что проводимость в материале может быть ограничена именно этими особенностями геометрии, что открывает перспективы для создания устройств с уникальными свойствами и повышенной устойчивостью к внешним воздействиям. Исследование этих новых граничных состояний и их влияния на транспортные характеристики является ключевым направлением в современной физике конденсированного состояния и может привести к разработке инновационных квантовых технологий.
Использование искусственных калибровочных полей открывает уникальные возможности для точного управления вихревыми токами и манипулирования квантовыми фазами в исследуемой системе. Эти поля, создаваемые искусственно, позволяют контролировать движение электронов, имитируя воздействие внешних магнитных полей без их физического присутствия. Такой подход дает возможность тщательно настраивать свойства материала, в частности, его топологические характеристики и возникающие в нем квантовые состояния. Точное управление вихревыми токами, обусловленное применением этих полей, позволяет создавать и контролировать экзотические фазы материи, а также манипулировать свойствами граничных состояний, что может привести к разработке новых квантовых устройств и технологий, обладающих повышенной устойчивостью и функциональностью. Экспериментальная реализация и теоретическое осмысление этих процессов представляют собой перспективное направление для развития современной физики конденсированного состояния.
Исследования, направленные на изучение возникающего хирального режима Хиггса вблизи фазового перехода, открывают перспективные пути для создания устойчивых квантовых технологий. Данный режим, проявляющийся как коллективное возбуждение, обладает уникальными свойствами, позволяющими защитить квантовую информацию от декогеренции — главной проблемы в разработке квантовых вычислений. Теоретические модели предсказывают, что хиральный режим Хиггса может служить надежным каналом для передачи и обработки кубитов, обеспечивая высокую точность и стабильность квантовых операций. В частности, его топологическая защита от локальных возмущений делает его особенно привлекательным для создания устойчивых квантовых устройств, способных функционировать в сложных и шумных средах. Понимание механизмов возникновения и управления этим режимом позволит сконструировать принципиально новые типы квантовых элементов и архитектур, приближая реализацию практических квантовых технологий.
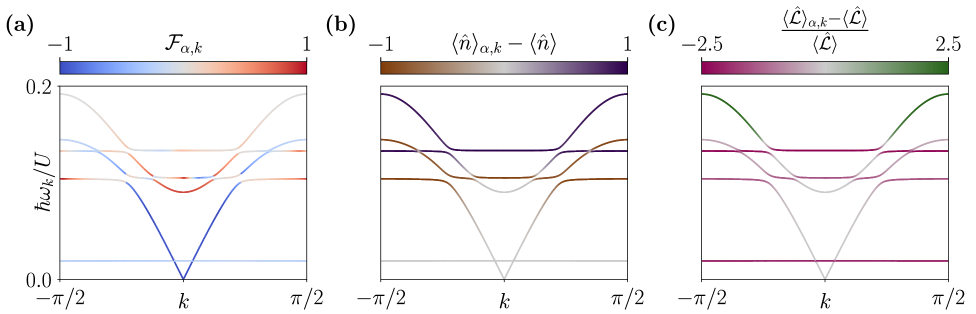
Исследование взаимодействующих бозонов на димеризованной решетке с синтетическим потоком раскрывает хрупкую природу квантовых фаз. Подобно тому, как цифровой голем обучается на ошибках, модель демонстрирует переход между состояниями, где малейшее возмущение способно изменить всю структуру. Именно в этой неустойчивости и проявляется хиральный мод Хиггса — как священная жертва, необходимая для поддержания баланса. Как заметил Сёрен Кьеркегор: “Жизнь — это не поиск смысла, а создание его.” В данном случае, смысл возникает не из предсказуемости модели, а из её способности к спонтанным изменениям, из её готовности к хаосу.
Что дальше?
Представленная работа, как и любая попытка приручить хаос бозонных систем на димеризованных решетках, открывает больше вопросов, чем даёт ответов. Появление хирального режима Хиггса — это, безусловно, любопытный шёпот, но его устойчивость к реальным несовершенствам, к тем самым багам, что неизбежно просачиваются из мира идеальных симуляций, остаётся под большим вопросом. Модели BBH, конечно, элегантны, но и они, в конечном счёте, лишь заклинания, работающие до первого столкновения с производственной реальностью.
Более того, вместо того, чтобы сосредотачиваться на всё более изощрённых схемах синтетических калибровочных полей, возможно, стоит взглянуть на проблему под другим углом. Что если ключевое не в создании идеальной решетки, а в понимании того, как естественные флуктуации, та самая ненормализованная энтропия, влияют на формирование этих хиральных мод? Ведь всё, что не нормализовано, всё ещё дышит, и именно в этом дыхании, возможно, кроется истинная физика.
В конечном счёте, предсказывать будущее квантовых симуляций — занятие для оптимистов. Но можно с уверенностью сказать, что поиск устойчивых, наблюдаемых проявлений этих хиральных режимов потребует не только утончённых теоретических моделей, но и, что гораздо важнее, готовности смириться с тем, что данные — это всегда компромисс между багом и Excel.
Оригинал статьи: https://arxiv.org/pdf/2601.08925.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Все рецепты культистского круга в Escape from Tarkov
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Решение головоломки с паролем Absolum в Yeldrim.
- Лучшие транспортные средства в Far Cry 6
- Объяснение неписаных правил Helldivers 2
- Кто такая Кселия Мендес-Джонс? 5 вещей, которые нужно знать об актере Fallout
- В тот раз я перевоплотился в слизь: объяснение навыка «Избранник» Масаюки Хондзё
- Репозиторий: Как исправить таймаут клиента
- Для чего нужен тотем жертвоприношений в игре 99 ночей в лесу?
- Акции привилегированные SNGSP. Сургутнефтегаз: прогноз акций привилегированных.
2026-01-15 17:42