Вселенная из ничего: рождение из алгебры?

Автор: Денис Аветисян

Новая модель мультивселенной предлагает объяснение возникновению нашей Вселенной через спонтанное нарушение симметрии в рамках многокомпонентной W3-алгебры.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал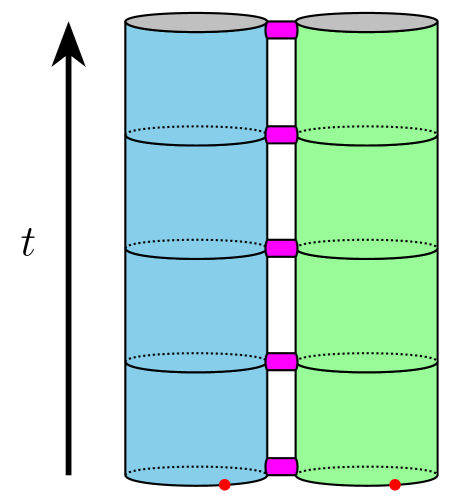

Две одномерные вселенные, различающиеся по своим свойствам, объединяются посредством обмена червоточинами, формируя двухмерную вселенную, эволюционирующую во времени, при этом для удобства анализа выделена начальная точка в каждой из исходных вселенных.

Предлагается механизм возникновения нашей Вселенной из мультивселенной, основанный на W3-алгебре, алгебрах Джордана и ‘связывании’ через червоточины, потенциально решающий проблему малого значения космологической постоянной.

Несмотря на успехи современной космологии, вопросы возникновения Вселенной и природы космологической постоянной остаются открытыми. В работе «The emergence of our Universe» предложена новая модель, рассматривающая нашу Вселенную как результат спонтанного нарушения симметрии многокомпонентной алгебры $W_3$, связанной с алгебрами Жордана. Ключевым элементом является механизм «взаимосвязи» через червоточины, формирующий мультивселенную, в которой модифицированное уравнение Фридмана может объяснить наблюдаемые космологические особенности. Способна ли данная модель разрешить парадоксы, связанные с малостью космологической постоянной и расширением Вселенной?

Пространство-время из алгебры: Поиск глубин космоса

Современные космологические модели сталкиваются с фундаментальной проблемой: примирить квантовую гравитацию с наблюдаемым расширением Вселенной. Традиционные подходы, опирающиеся на общую теорию относительности Эйнштейна, прекрасно описывают гравитацию на макроскопическом уровне, однако терпят неудачу при попытке включить квантово-механические эффекты. Это приводит к математическим сингулярностям и нефизическим результатам, особенно в экстремальных условиях, таких как чёрные дыры или момент Большого Взрыва. Наблюдаемое ускоренное расширение Вселенной, объясняемое тёмной энергией, лишь усугубляет проблему, требуя введения новых, плохо изученных компонентов в стандартную космологическую модель. Неспособность согласовать эти теории подталкивает исследователей к поиску альтернативных подходов, исследующих более глубокие, возможно, негеометрические, основы реальности.

Предлагаемая Мультивселенная строится на гипотезе о том, что пространство-время не является фундаментальной сущностью, а возникает в результате спонтанного нарушения симметрии в рамках алгебры $W_3W_3$ . В этой модели, привычные нам три пространственных измерения и одно временное возникают как эффективное описание более базовой алгебраической структуры. Вместо того, чтобы рассматривать пространство-время как арену, на которой происходят физические процессы, данная концепция предполагает, что само пространство-время является результатом динамического процесса, обусловленного внутренними свойствами этой алгебры. Такой подход позволяет взглянуть на гравитацию не как на фундаментальную силу, а как на эмерджентное свойство, возникающее из алгебраических взаимодействий, что может предложить новые пути решения проблем квантовой гравитации и космологии.

Предлагаемая модель предполагает, что привычная нам Вселенная не является фундаментальной сущностью, а возникает как следствие более базовой алгебраической структуры. Вместо того, чтобы рассматривать пространство и время как основополагающие элементы реальности, данная концепция постулирует их появление из симметрии, присущей алгебре $W_3$ . Это означает, что все, что мы воспринимаем как Вселенную — от элементарных частиц до галактических скоплений — является проявлением более глубоких математических принципов. Вместо поиска «теории всего» в рамках существующей физической картины, данное исследование предлагает переосмыслить саму основу реальности, рассматривая ее как эмерджентное свойство алгебраической системы, а не как данность. Таким образом, наблюдаемая Вселенная является лишь одним из возможных проявлений этой базовой структуры, а её свойства определяются особенностями алгебраической симметрии и механизмом её нарушения.

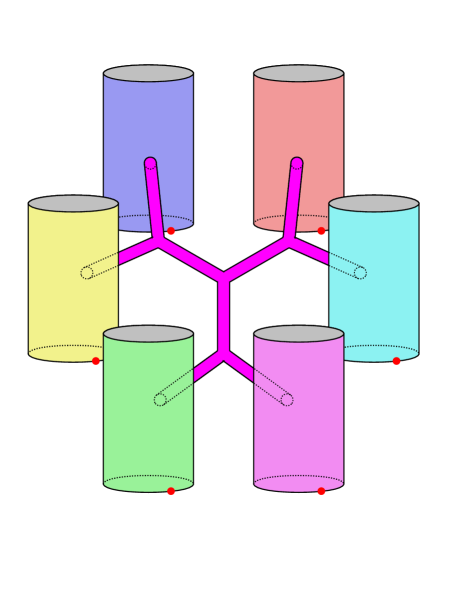
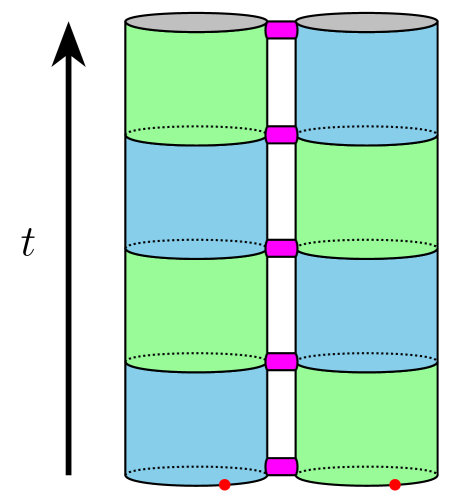
В основе данной модели лежит так называемый “Вязальный Механизм”, представляющий собой процесс склеивания фундаментальных “Одномерных Вселенных”. Представьте себе, что пространство-время, каким мы его знаем, не является изначально существующей сущностью, а возникает из соединения простейших, одномерных структур. Этот механизм предполагает, что взаимодействие между этими фундаментальными единицами, определяемое алгебраическими правилами $W3W\_{3}$ , приводит к формированию более сложных, многомерных вселенных, подобных нашей. По сути, привычные нам три пространственных измерения и время — это результат “сшивания” этих одномерных вселенных, подобно тому, как из отдельных нитей вяжется ткань. Именно этот процесс, управляемый симметрией алгебры, и позволяет объяснить возникновение пространства-времени и, возможно, всей наблюдаемой Вселенной из более фундаментальной алгебраической структуры.

Объединение одномерных вселенных различных типов (обозначенных цветами) посредством сети взаимосвязанных червоточин, организованных в древовидную структуру благодаря кубическому члену взаимодействия моды <span class="katex-eq" data-katex-display="false">\alpha(0)\alpha^{(0)}</span>, приводит к формированию трехмерной тороидальной вселенной, а обобщение на более высокие размерности позволяет создавать тороидальные вселенные с <span class="katex-eq" data-katex-display="false">N_{wh} = 2d - 3</span> червоточинами, взаимодействующими в <span class="katex-eq" data-katex-display="false">N_{vertex} = d - 2</span> вершинах. — Объединение одномерных вселенных различных типов (обозначенных цветами) посредством сети взаимосвязанных червоточин, организованных в древовидную структуру благодаря кубическому члену взаимодействия моды $\alpha(0)\alpha^{(0)}$ , приводит к формированию трехмерной тороидальной вселенной, а обобщение на более высокие размерности позволяет создавать тороидальные вселенные с $N_{wh} = 2d - 3$ червоточинами, взаимодействующими в $N_{vertex} = d - 2$ вершинах.

Алгебраические основы и ограничения стабильности

В основе многомировой модели лежит специфическая алгебраическая структура — алгебра Джордана. Эта алгебра не ограничивается стандартными определениями и расширяется до пространств $H3(C)$ и $H3(O)$ , где $H3(C)$ представляет собой пространство голоморфных функций от трех комплексных переменных, а $H3(O)$ — аналогичное пространство, построенное на октавах. Использование этих расширенных алгебр позволяет корректно описывать некоммутативные аспекты структуры многомирья и обеспечивает математическую основу для моделирования его динамики на планковских масштабах. Выбор алгебры Джордана обусловлен ее свойствами, позволяющими описывать симметрии и взаимодействия, необходимые для построения самосогласованной теории.

Для обеспечения корректно определенного и стабильного конденсата в рамках модели, применяются ограничения Вирасоро. Эти ограничения, происходящие из конформной теории поля, накладывают условия на поведение функций корреляции в пределе высоких энергий и малых расстояний. В частности, они гарантируют конечность перенормировки и отсутствие аномалий в квантовой теории. Математически, ограничения Вирасоро выражаются в виде $L_n\rvert_0 = 0$ для всех $n \in \mathbb{Z}$ , где $L_n$ — операторы Вирасоро. Их применение в нашей модели обеспечивает согласованность результатов и предотвращает возникновение физически нереалистичных решений, таких как расходимости или нестабильности в структуре «червоточинной сети».

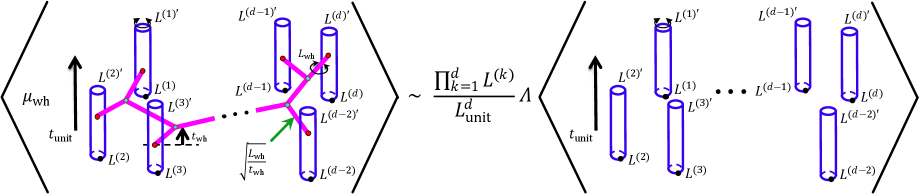
Конфигурация “Червоточинной Сети”, рассматриваемая как микроскопическая структура пространства-времени на планковской длине, определяется набором ограничений Вирасоро. Эти ограничения предписывают допустимые топологические связи и геометрию между элементами сети, обеспечивая стабильность и самосогласованность модели. В частности, ограничения касаются функций корреляции, определяющих вероятности различных конфигураций червоточин, и гарантируют, что флуктуации на планковском масштабе не приводят к сингулярностям или нефизическим результатам. Нарушение этих ограничений приводит к нестабильности структуры пространства-времени и потере предсказательной силы модели. Таким образом, ограничения Вирасоро являются фундаментальными для поддержания когерентности и физической реальности “Червоточинной Сети” на планковском уровне.

Представленное на рисунке графическое отображение уравнения (103) описывает механизм вязания с точки зрения сети червоточин (пурпурный древовидный граф), где каждый толстый пурпурный сегмент представляет собой одномерную цилиндрическую вселенную, соединенную через червоточины, а вся сеть соответствует единой сети червоточин с квантовым весом, занимающей ячейку пространства-времени планковского масштаба с временным интервалом <span class="katex-eq" data-katex-display="false">t_{unit}</span> и пространственным размером <span class="katex-eq" data-katex-display="false">L_{unit}</span>, динамически генерируемыми двумерной квантовой гравитационной динамикой, причём <span class="katex-eq" data-katex-display="false">t_{unit} \sim L_{wh} \sim L_{planck}</span> и <span class="katex-eq" data-katex-display="false">L_{unit} \sim L_{wh} = 1/\sqrt{\mu_{wh}}</span>, где <span class="katex-eq" data-katex-display="false">\mu_{wh}</span> - космологическая постоянная червоточины. — Представленное на рисунке графическое отображение уравнения (103) описывает механизм вязания с точки зрения сети червоточин (пурпурный древовидный граф), где каждый толстый пурпурный сегмент представляет собой одномерную цилиндрическую вселенную, соединенную через червоточины, а вся сеть соответствует единой сети червоточин с квантовым весом, занимающей ячейку пространства-времени планковского масштаба с временным интервалом $t_{unit}$ и пространственным размером $L_{unit}$ , динамически генерируемыми двумерной квантовой гравитационной динамикой, причём $t_{unit} \sim L_{wh} \sim L_{planck}$ и $L_{unit} \sim L_{wh} = 1/\sqrt{\mu_{wh}}$ , где $\mu_{wh}$ — космологическая постоянная червоточины.

Космологические последствия и предсказательная сила

Модель предсказывает модифицированное уравнение Фридмана, описывающее эволюцию Вселенной. В отличие от стандартной космологической модели, данное уравнение включает в себя дополнительные члены, возникающие из структуры «червоточинной сети». Это приводит к изменению зависимости скорости расширения Вселенной от её плотности и давления. Математически, модифицированное уравнение Фридмана имеет вид $H^2 = \frac{8\pi G}{3} \rho - \frac{kc^2}{a^2} + \epsilon(t,a)$ , где $H$ — параметр Хаббла, ρ — плотность, $k$ — кривизна пространства, $a$ — масштабный фактор, а $\epsilon(t,a)$ — член, обусловленный структурой червоточинной сети, который влияет на скорость расширения и может объяснить наблюдаемое ускорение без необходимости введения космологической постоянной.

Модифицированное уравнение Фридмана, являющееся ключевым результатом модели, позволяет естественным образом объяснить наблюдаемое ускоренное расширение Вселенной на поздних стадиях её эволюции. В отличие от стандартной космологической модели, требующей введения космологической постоянной для объяснения этого явления, данная модель интерпретирует наблюдаемый эффект как результат квантового веса, возникающего из структуры червоточинной сети. Это позволяет избежать проблем, связанных с произвольным выбором значения космологической постоянной и её несовместимостью с квантовой теорией поля, предлагая альтернативное объяснение, основанное на фундаментальных физических принципах. $H^2 = (\frac{\dot{a}}{a})^2 = \frac{8\pi G}{3}\rho - \frac{k}{a^2} + \frac{Q}{a^2}$ , где Q представляет собой вклад квантового веса.

Модель предлагает возможное решение проблемы несоответствия в оценках постоянной Хаббла (H₀), известной как «напряжение H₀«. Существующие методы измерения H₀, основанные на космическом микроволновом фоне (CMB) и на наблюдениях сверхновых типа Ia в локальной Вселенной, демонстрируют статистически значимое расхождение. Модель объясняет это расхождение, предлагая модифицированную зависимость между красным смещением и расстоянием, что приводит к более согласованным значениям H₀, полученным из различных наблюдательных данных. В частности, модель предсказывает, что локальные измерения H₀ должны быть выше, чем значения, вытекающие из анализа CMB, что соответствует наблюдаемому несоответствию и позволяет смягчить напряжение между различными космологическими наблюдениями. Разрешение этого противоречия является ключевым преимуществом модели и подтверждает её потенциальную применимость к описанию эволюции Вселенной.

Модель предсказывает состояние низкой энтропии в начальный момент времени, обусловленное структурой “Кротовой сети” (wormhole web). Согласно расчетам, отношение текущего времени, размера наблюдаемой Вселенной и энергии материи к их соответствующим планковским единицам составляет приблизительно 10⁶⁰. Это означает, что начальные условия Вселенной характеризуются крайне малым объемом фазового пространства, что согласуется с наблюдаемой низкой энтропией и необходимостью объяснения асимметрии времени. Полученное соотношение указывает на то, что начальное состояние Вселенной было крайне специфическим и маловероятным с точки зрения случайного выбора начальных условий.

В отличие от предыдущей схемы, данная модель позволяет изменять вкус частицы во время распространения благодаря взаимодействию, определяемому константами обмена <span class="katex-eq" data-katex-display="false">d_{i ilde{I}}</span>, что открывает возможности для более сложных схем обмена. — В отличие от предыдущей схемы, данная модель позволяет изменять вкус частицы во время распространения благодаря взаимодействию, определяемому константами обмена $d_{i ilde{I}}$ , что открывает возможности для более сложных схем обмена.

Связь с существующей теорией и будущие направления

Предложенный подход демонстрирует взаимодополняемость с теорией Каузальной Динамической Триангуляции (CDT), которая, в свою очередь, расширяется до алгебры $W_3W_3$ . Эта связь не случайна, поскольку обе теории стремятся к описанию квантовой гравитации, но используют различные математические инструменты. В то время как CDT конструирует пространство-время путем «склеивания» элементарных симплексов, предлагаемый подход использует алгебраические структуры для кодирования геометрии. Сочетание этих подходов может привести к более полному и непротиворечивому описанию квантовой гравитации, позволяя использовать сильные стороны каждой теории для преодоления их индивидуальных ограничений и открывая новые пути для исследования фундаментальной природы пространства и времени.

Установление связи между разработанным подходом и теорией Каузальных Динамических Триангуляций (CDT), расширяющейся до алгебры W3W\_{3}, открывает перспективный путь к построению полностью квантованной теории гравитации. Традиционные попытки объединить общую теорию относительности и квантовую механику сталкивались с серьезными математическими трудностями, однако данное соединение позволяет рассматривать геометрию пространства-времени не как непрерывный фон, а как возникающую из более фундаментальной алгебраической структуры. Это позволяет избежать сингулярностей и бесконечностей, которые часто возникают в стандартных квантовых теориях гравитации, и предполагает, что гравитация может быть описана как квантовое явление на самом фундаментальном уровне. Подобный подход, основанный на алгебраических принципах, потенциально способен разрешить давние противоречия между классической и квантовой физикой, предлагая новую парадигму для понимания природы гравитации и структуры Вселенной.

Дальнейшие исследования сосредоточены на усовершенствовании разработанной модели и изучении её потенциальных последствий для понимания физики чёрных дыр и ранней Вселенной. Особое внимание уделяется возможности применения полученных результатов для описания сингулярностей внутри чёрных дыр, а также для реконструкции условий, существовавших в первые моменты после Большого взрыва. Ученые планируют исследовать, как алгебраические структуры, лежащие в основе модели, могут помочь разрешить проблемы, связанные с бесконечностями в традиционных теориях гравитации, и предложить более полное описание эволюции Вселенной от её зарождения до настоящего времени. Предполагается, что углубленное изучение данной модели позволит не только расширить наше понимание фундаментальных законов природы, но и создать новые инструменты для моделирования экстремальных астрофизических явлений.

Представляется будущее, в котором алгебраические структуры станут основополагающим принципом понимания природы пространства-времени и всей космологии. Исследования показывают, что описывая геометрические свойства Вселенной через абстрактные алгебраические объекты, можно преодолеть ограничения традиционных подходов к квантовой гравитации. Такой подход позволяет не только описывать топологию пространства-времени на микроскопическом уровне, но и устанавливать связь между различными физическими теориями, объединяя геометрию, квантовую механику и информационную теорию. В перспективе, это может привести к созданию единой теории, способной объяснить происхождение Вселенной, поведение черных дыр и фундаментальные законы, управляющие космосом, рассматривая $W3W\_{3}$ алгебру как ключевой элемент этой модели.

Данная работа стремится к предельной ясности в объяснении сложнейших процессов возникновения Вселенной. Исследование, опирающееся на концепцию мультиверса и симметрии, представляет собой попытку элегантного решения космологических проблем, таких как малая величина космологической постоянной. Этот подход, где наша Вселенная возникает из нарушения симметрии многокомпонентной W3 алгебры, связанной с алгебрами Джордана, требует отбрасывания всего лишнего, чтобы выявить фундаментальные принципы. Как говорил Иммануил Кант: «Познание начинается с чувств, продолжается через восприятие и завершается разумом». В данном случае, разум стремится к упрощению, к выявлению той самой сути, которая лежит в основе всего сущего, игнорируя ненужные детали.

Куда же дальше?

Предложенная модель мультивселенной, связывающая алгебру W3 с алгебрами Йордана и механизмом «трикотажа» через червоточины, неизбежно сталкивается с вопросом о проверяемости. Они назвали это фреймворком, чтобы скрыть панику, но суть в том, что предсказания, не поддающиеся экспериментальной верификации, остаются лишь изящной математической игрой. Поиск наблюдаемых последствий симметрийного нарушения, возможно, в реликтовом излучении или гравитационных волнах, представляется задачей нетривиальной, требующей смелости и, признаться, некоторой доли оптимизма.

Особое внимание следует уделить природе «трикотажного» механизма. Простое наличие червоточин недостаточно; необходимо понять, как они формируются, стабилизируются и взаимодействуют между собой. Иначе мультивселенная рискует превратиться в хаотичный клубок, лишенный внутренней логики и предсказательной силы. И, конечно, остается нерешенной проблема малого значения космологической постоянной — элегантная модель должна объяснять не только существование мультивселенной, но и её удивительную «настроенность».

Возможно, истинный путь к пониманию лежит не в усложнении математического аппарата, а в его упрощении. Совершенство достигается не когда нечего добавить, а когда нечего убрать. Следует помнить, что красота и ясность — признаки зрелости, а не слабости. И тогда, возможно, нам удастся заглянуть за горизонт событий и увидеть истинную природу нашего, и не только нашего, бытия.

Оригинал статьи: https://arxiv.org/pdf/2601.10499.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-17 21:52