Искажение света: за пределами упрощенной оптики

Автор: Денис Аветисян

Новое исследование предлагает более точный метод расчета эффектов гравитационного линзирования, выходящий за рамки традиционного геометрического приближения.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал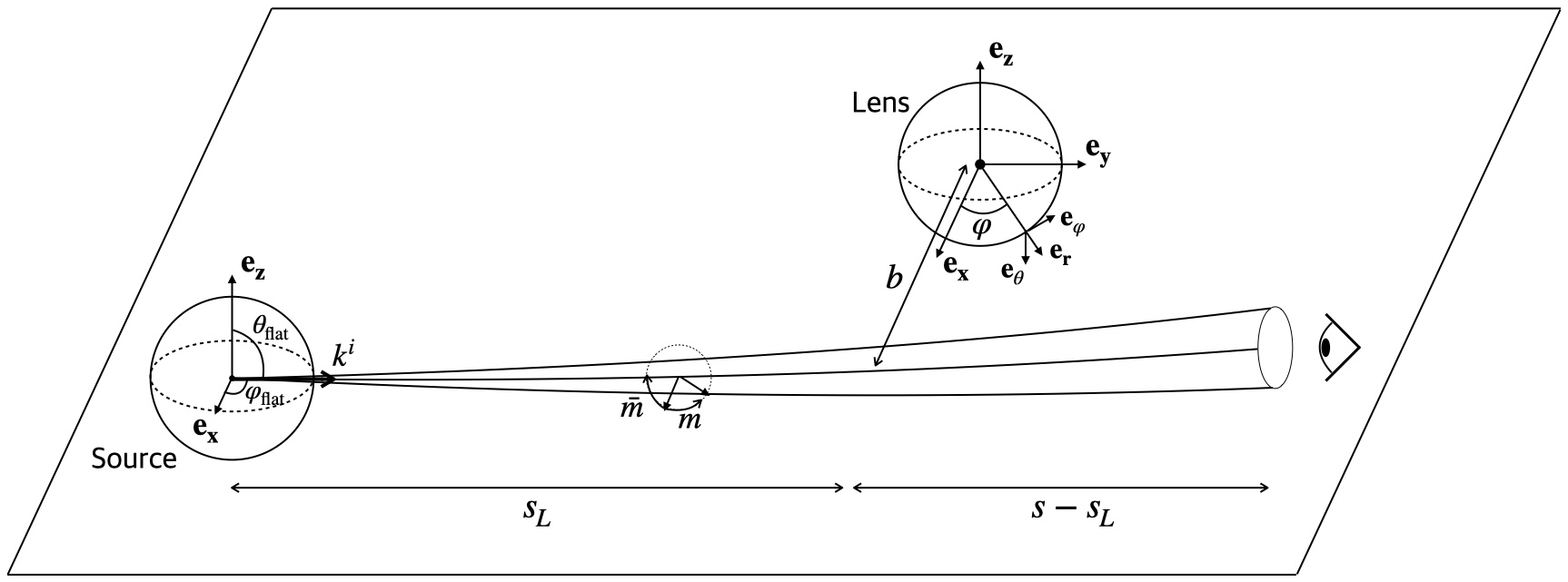

В рамках исследования метрики линз, координатная система строится вокруг оптической оси, где минимальное радиальное расстояние до точки отклонения геодезической соответствует параметру удара, а при определении начальных условий вблизи источника используется плоская приближенная модель пространства, центрированная на самом источнике, что позволяет детально описать поведение света в искривленном пространстве-времени.

В статье представлен пертурбативный подход к вычислению поправок к геометрической оптике для гравитационного линзирования, демонстрирующий отсутствие фазового сдвига первого порядка, пропорционального GM/ω, и важность отслеживания динамики поправок первого порядка BE.

В традиционном описании гравитационного линзирования, основанном на эйкональном приближении, волновые эффекты часто игнорируются как вторые по порядку. Данная работа, озаглавленная ‘Gravitational lensing beyond the eikonal approximation’, исследует волновые эффекты, возникающие при распространении скалярных волн в искривленном пространстве-времени, используя формализм Ньюмана-Пенроуза. Показано, что в вакууме волновые поправки начинаются с порядка $G^2$, в то время как в среде с ненулевой плотностью вещества — уже с порядка $G$. Каким образом учет динамики этих поправок первого порядка может повлиять на точность анализа сигналов гравитационных волн и построение моделей компактных объектов?

За пределами геометрической оптики: Необходимость волновых коррекций

Геометрическая оптика, предоставляющая удобное и эффективное приближение для описания распространения волн, основана на представлении света в виде лучей, движущихся по прямым линиям. Однако, эта модель теряет свою актуальность, когда длина волны света становится сопоставимой с размерами препятствий или деталей рассматриваемой системы. В таких случаях, явления дифракции и интерференции становятся существенными, и лучевая оптика не способна адекватно предсказать наблюдаемую картину. Вместо четких теней и резких границ, свет огибает препятствия, создавая сложные дифракционные картины, что требует использования более сложных волновых моделей для точного анализа и моделирования.

Для точного моделирования волновых явлений необходимо учитывать эффекты дифракции, что требует внесения поправок, выходящих за рамки приближения геометрической оптики. В то время как лучевая оптика успешно описывает распространение волн в ситуациях, когда длина волны значительно меньше размеров препятствий, при приближении длины волны к этим размерам возникают заметные отклонения от предсказаний лучевой оптики. Дифракция, проявляющаяся в огибании волнами препятствий и интерференции, становится доминирующим фактором, влияющим на картину распространения. Игнорирование этих эффектов приводит к неточностям в моделировании, особенно в задачах, связанных с микро- и нанооптикой, где размеры структур сопоставимы с длиной волны света. Таким образом, для получения адекватного описания волновых процессов необходим переход к более сложным моделям, учитывающим дифракцию и требующим применения соответствующих математических методов.

Традиционные методы вычисления поправок, необходимых для точного моделирования волновых эффектов, такие как дифракционный интеграл, зачастую предъявляют высокие требования к вычислительным ресурсам и характеризуются значительной сложностью. Вычисление интеграла требует учета интерференции волн, рассеянных на различных точках апертуры или препятствия, что приводит к многомерным вычислениям, особенно при высокой разрешающей способности. Решение этого интеграла может быть крайне затратным по времени и памяти, что делает его непрактичным для задач, требующих оперативных расчетов или моделирования сложных систем. Кроме того, сложность интеграла возрастает при увеличении детализации моделируемой структуры, что вынуждает исследователей искать альтернативные, более эффективные численные методы для преодоления этих вычислительных ограничений и обеспечения приемлемого времени расчетов.

Расширение BE: Новый взгляд на волновые амплитуды

Расширение BE (Born-Enhanced) представляет собой пертурбативный подход к вычислению поправок к геометрической оптике, концентрируясь на коррекциях первого порядка к амплитуде волны. В отличие от интегральных методов, требующих значительных вычислительных ресурсов, расширение BE использует ряд разложений для представления волнового поля. Это позволяет эффективно рассчитывать отклонения от идеального поведения, предсказываемого геометрической оптикой, особенно в ситуациях, когда приближения, лежащие в основе геометрической оптики, больше не применимы. Основной целью является точное определение амплитудных изменений, вызванных, например, рассеянием или дифракцией, сохраняя при этом вычислительную эффективность.

Метод BE-расширения использует ряд разложений для представления волнового поля, предоставляя вычислительно эффективную альтернативу интегральным подходам. В отличие от методов, требующих численного интегрирования волновых функций по всему пространству, BE-расширение аппроксимирует решение в виде ряда, что существенно снижает вычислительную сложность. Это достигается путем представления волнового поля в виде суммы членов, каждый из которых соответствует определенному порядку разложения. Такой подход особенно эффективен при моделировании распространения волн в системах с умеренными изменениями показателя преломления, где сходимость ряда обеспечена, и позволяет получить приближенное решение с высокой точностью при значительно меньших вычислительных затратах, чем при использовании прямых методов решения интегральных уравнений.

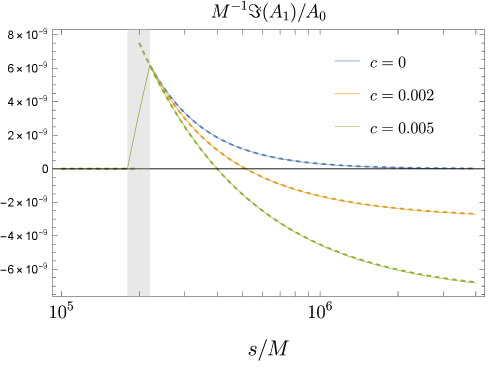
В основе метода BE-расширения лежит точное определение и количественная оценка фазового сдвига, возникающего в волне, что является ключевым фактором для его предсказательной способности. Анализ показывает отсутствие фазового сдвига первого порядка, пропорционального произведению гравитационной массы $G$ на массу $M$ и обратного значения частоты ω. Это означает, что при расчете поправок к геометрической оптике с использованием BE-расширения, данный член можно пренебречь, упрощая вычисления и повышая точность моделирования волновых процессов.

Расширение BE включает в себя частотно-зависимую фазовую модуляцию, уточняющую описание поведения волны после прохождения через тонкую линзу. Вычисленная фазовая задержка пропорциональна $Σ/ω$ , где Σ — суммарная кривизна линзы, а ω — угловая частота. При этом, величина фазового сдвига уменьшается пропорционально $(sL/s)^2$ , где $s$ — пространственная частота, а $L$ — длина линзы, что указывает на ослабление влияния фазовой модуляции с увеличением пространственной частоты и длины линзы.

Искривление пространства-времени и распространение волн: От теории к реальности

Распространение волн в гравитационном поле определяется кривизной пространства-времени, количественно описываемой тензором Риччи $R_{\mu\nu}$ . Этот тензор представляет собой сжатие тензора кривизны Римана и отражает влияние распределения массы и энергии на геометрию пространства-времени. Уравнения, описывающие распространение волн, такие как волновое уравнение, в общей теории относительности модифицируются кривизной пространства-времени, выраженной через тензор Риччи и скалярную кривизну $R$ . Отклонения от евклидовой геометрии, определяемые тензором Риччи, приводят к искривлению траекторий волн и изменению их частоты, что проявляется в эффектах гравитационного красного смещения и гравитационного линзирования. Анализ тензора Риччи позволяет предсказывать и объяснять наблюдаемые аномалии в распространении электромагнитных и гравитационных волн вблизи массивных объектов.

Приближение слабого поля существенно упрощает анализ искривления пространства-времени, позволяя моделировать эффекты гравитационного линзирования. В рамках этого приближения, метрика пространства-времени представляется как возмущение плоского пространства Минковского, где возмущения малы по сравнению с общей метрикой. Это позволяет использовать линейную теорию гравитации и решать уравнения Эйнштейна в упрощенной форме. В частности, отклонение световых лучей, вызванное гравитацией массивных объектов, рассчитывается на основе этих упрощенных уравнений, что позволяет предсказывать и объяснять наблюдаемые эффекты гравитационного линзирования, такие как множественные изображения источников света и искажение их формы. Расчеты основаны на определении тензора возмущений метрики $h_{\mu\nu}$ и решении уравнений для него.

Подсистема отклонения геодезических предоставляет методы решения для траектории референтной геодезической и связанных с ней величин пространства-времени, что критически важно для моделирования путей распространения волн. Решение уравнений геодезических отклонений позволяет определить, как близкие геодезические расходятся или сближаются под влиянием гравитации, описываемой тензором Риччи. В частности, вычисление так называемого “аффинного параметра” вдоль геодезической, а также анализ тензора отклонения $\delta K^\mu$ , обеспечивает количественную оценку этого отклонения. Это необходимо для точного моделирования распространения электромагнитных и гравитационных волн в искривленном пространстве-времени, поскольку траектория волны определяется геодезической, а отклонения от прямой линии указывают на гравитационное влияние.

Разложение Эйконаля представляет собой математический аппарат, позволяющий выразить волновое уравнение в терминах амплитуды и фазы. В рамках данного подхода, волна описывается как семейство поверхностей постоянной фазы, а ее распространение анализируется через функцию фазы $S(x)$ . Ключевым элементом является использование понятия ареального расстояния $r$ , представляющего собой координату, измеряющую расстояние вдоль двумерной поверхности, и нулевого волнового вектора $k$ , удовлетворяющего условию $k^2 = 0$ . Это позволяет упростить анализ распространения волн в искривленном пространстве-времени, особенно в контексте гравитационного излучения и астрофизических задач, где точное решение полного волнового уравнения затруднительно.

Гравитационное линзирование и моделирование звезд: От теории к наблюдаемым эффектам

Решение уравнений Толмана-Оппенгеймера-Волкова (TOV) предоставляет физически обоснованную модель распределения массы для гравитационного линзирования. Это решение, описывающее сферически симметричные звезды, позволяет учитывать влияние гравитации на искривление пространства-времени вокруг массивных объектов, что является ключевым фактором в расчете отклонения света. В отличие от упрощенных моделей, решение TOV учитывает изменение давления и плотности внутри звезды, что приводит к более точному определению гравитационной линзы. Такой подход особенно важен при изучении линзирования, вызванного галактиками и другими компактными объектами, где внутреннее строение линзирующего объекта существенно влияет на наблюдаемую картину. Использование решения TOV в сочетании с другими методами, такими как приближение слабого поля, позволяет с высокой точностью предсказывать и интерпретировать явления гравитационного линзирования, открывая возможности для изучения распределения темной материи и параметров космологической модели.

Сочетание решения Толова (TOV) — описывающего сферически симметричные звезды — с приближением слабого поля и расчетами гравитационного линзирования Риччи позволяет предсказывать отклонение света вблизи этих объектов. Решение TOV предоставляет реалистичную модель распределения массы, а приближение слабого поля упрощает расчеты, позволяя аналитически оценить гравитационное воздействие. Применение расчетов Риччи, основанных на искривлении пространства-времени, дает возможность количественно определить угол отклонения световых лучей, проходящих вблизи массивных тел. Такой подход не только подтверждает предсказания общей теории относительности, но и позволяет использовать гравитационное линзирование как инструмент для изучения свойств звезд и галактик, а также для исследования распределения темной материи во Вселенной. Точность предсказаний зависит от корректного учета параметров звездной модели и приближений, используемых в расчетах.

Для более точного анализа явлений гравитационного линзирования используются методы приближения тонкой линзы и учет эффекта гравитационного замедления времени. Приближение тонкой линзы, упрощая геометрию задачи, позволяет эффективно рассчитывать отклонение света, особенно в случаях, когда расстояние до линзирующего объекта значительно превышает его размер. В свою очередь, учет гравитационного замедления времени, возникающего из-за разницы в гравитационном потенциале между наблюдателем и линзирующим объектом, вносит важную поправку в расчет времени прохождения света, позволяя более точно определить расстояния и параметры линзирующего объекта. Комбинация этих техник позволяет получить детальное представление о распределении массы в линзирующем объекте и подтвердить предсказания общей теории относительности в сильных гравитационных полях.

Альтернативный подход к расчету фазовых сдвигов представлен методом разложения в частные волны, который дополняет стандартное разложение в бозонные экспоненты (BE). Исследования показали, что разложение в частные волны демонстрирует устойчивый фазовый сдвиг, пропорциональный отношению $\overline{\kappa}$ к $\overline{\omega}$ даже на значительном удалении от линзирующего объекта. Данный эффект указывает на то, что фазовые сдвиги, вызванные гравитационным линзированием, могут сохраняться на больших расстояниях, что имеет важное значение для интерпретации наблюдаемых искажений изображений далеких источников и для более точного моделирования распределения массы в гравитационных линзах. Этот подход позволяет более детально исследовать структуру гравитационного поля и выявлять тонкие эффекты, которые могут быть упущены при использовании стандартных методов.

Для небольшой галактики с массой $10^9$ масс Солнца, радиусом в 1 килопарсек, находящейся на расстоянии 100 мегапарсек и подверженной воздействию излучения с длиной волны $10^{11}$ метров, величина первой поправки в рамках BE-приближения составляет приблизительно -4 x 10^-6. Данное значение демонстрирует, что даже при относительно скромных параметрах галактики и длине волны излучения, поправки, вносимые BE-приближением, хоть и малы, но могут оказаться значимыми для высокоточных измерений эффектов гравитационного линзирования. Подобные расчеты позволяют оценить вклад различных факторов в искажение световых лучей и уточнить модели распределения массы в гравитационных линзах.

Для корректного применения геометрической оптики при изучении гравитационного линзирования, необходимо выполнение условия $ω̄ ≫ 1$ . Данное требование, описывающее частоту света по отношению к характерной частоте гравитационных волн, оказывается более мягким, чем традиционное условие $κ̄ω̄ ≫ 1$ , где $κ̄$ представляет собой среднюю сходимость линзы. Более того, это условие тесно связано с длиной волны света λ, которая должна быть значительно меньше, чем отношение квадрата ударного параметра $b²$ к характерному масштабу длины линзы $L$ . Соблюдение этих критериев гарантирует, что свет распространяется по траекториям, предсказываемым геометрической оптикой, что позволяет точно моделировать эффекты гравитационного линзирования и извлекать информацию о свойствах линзирующего объекта.

Численное и аналитическое решения промежуточных величин, включая <span class="katex-eq" data-katex-display="false">\Im(A_1)/A_0</span>, согласуются при <span class="katex-eq" data-katex-display="false">R/R_S = 10^4</span> и <span class="katex-eq" data-katex-display="false">r_i/R_S = 2.5 \times 10^5</span>, при этом вертикальные полосы указывают на область звезды, где плотность материала <span class="katex-eq" data-katex-display="false">\rho_{mat} \neq 0</span>. — Численное и аналитическое решения промежуточных величин, включая $\Im(A_1)/A_0$ , согласуются при $R/R_S = 10^4$ и $r_i/R_S = 2.5 \times 10^5$ , при этом вертикальные полосы указывают на область звезды, где плотность материала $\rho_{mat} \neq 0$ .

Статья демонстрирует, что предсказание поведения света в искривленном пространстве-времени требует учета не только базовой геометрии, но и тонких поправок, возникающих из-за динамики первого порядка BE-разложения. Это напоминает о сложности систем, где даже небольшие изменения могут привести к непредсказуемым последствиям. Как однажды заметил Ричард Фейнман: «Самая глубокая и важная вещь в науке — это предсказание, которое оказалось неверным». Ведь именно осознание границ наших моделей и постоянное стремление к уточнению приближений позволяют приблизиться к пониманию вселенной, где даже гравитационное линзирование оказывается более сложным, чем казалось на первый взгляд.

Что Дальше?

Представленный анализ отклонений от геометрической оптики в гравитационном линзировании, хотя и демонстрирует отсутствие фазового сдвига, пропорционального GM/ω на ведущем порядке, лишь обнажает сложность предсказания судьбы сигнала. Каждый шаг к большей точности, каждая попытка учесть динамику поправок первого порядка BE, — это не столько решение проблемы, сколько усложнение модели, приближение к неминуемому каскаду зависимостей. Разделение системы на компоненты — в данном случае, отказ от эйконального приближения — не избавляет от общей хрупкости.

В конечном счете, стремление к более точным расчетам лишь откладывает неизбежное: всё связанное когда-нибудь упадёт синхронно. Следующим шагом представляется не столько поиск новых членов в пертурбативном разложении, сколько исследование устойчивости полученных результатов к малейшим изменениям начальных условий. Ведь даже самые изящные математические конструкции — лишь временные барьеры против энтропии.

Будущие исследования, вероятно, будут вынуждены признать, что сама концепция «сигнала» подвержена искажениям, что гравитационное линзирование — это не просто оптический эффект, а проявление фундаментальной взаимосвязанности всего сущего. И тогда, возможно, станет ясно, что попытка «построить» точную модель — это иллюзия, а задача исследователя — лишь наблюдать за тем, как система растёт и увядает.

Оригинал статьи: https://arxiv.org/pdf/2601.10239.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-18 08:00