Автор: Денис Аветисян
Новое исследование показывает, что даже слабое взаимодействие между упорядоченными и хаотичными квантовыми системами оказывает заметное влияние на их спектральные характеристики.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал
Экспериментальное изучение связанных квантовых бильярдов с интегрируемой и хаотичной классической динамикой и проверка специальной модели Розенцвейга-Портера.
Несмотря на значительный прогресс в понимании квантического хаоса, влияние даже слабого взаимодействия между системами с интегрируемой и хаотической классической динамикой остаётся недостаточно изученным. В работе «Experimental study of coupled quantum billiards with integrable and chaotic classical dynamics and test of a special Rosenzweig-Porter model» представлено экспериментальное исследование спектральных свойств двух связанных квантовых бильярдов, демонстрирующее, что взаимодействие приводит к заметным изменениям в их спектрах. Показано, что эти изменения могут быть эффективно описаны модифицированной моделью Розенцвейга-Портера, что позволяет оценить силу связи между системами. Какие новые возможности для изучения сложных квантовых систем открывает применение моделей случайных матриц к связанным системам с различной динамикой?
От порядка к хаосу: исследование квантовых бильярдов
Понимание перехода от предсказуемой, интегрируемой классической динамики к хаотическому поведению представляет собой фундаментальную задачу в физике. Этот переход, отражающий потерю детерминированности и предсказуемости, имеет ключевое значение для широкого спектра систем — от движения планет и молекул до турбулентности в жидкостях и поведения финансовых рынков. Изучение этого перехода требует не только математического аппарата классической механики, но и привлечения принципов квантовой механики, поскольку на микроскопическом уровне детерминированность может быть нарушена. Исследователи стремятся выявить универсальные закономерности, определяющие этот переход, и разработать инструменты для прогнозирования и управления хаотическими системами, что имеет важное значение для многих областей науки и техники. По сути, задача заключается в определении того, при каких условиях небольшие изменения в начальных условиях могут привести к экспоненциально растущим отклонениям в траекториях системы, что и характеризует хаотическое поведение.
Квантовые бильярды представляют собой идеализированные системы, используемые для моделирования волновых процессов в ограниченных областях, что позволяет физикам детально исследовать переход от предсказуемой, упорядоченной классической динамики к хаотическому поведению. Эти системы, по сути, являются аналогами бильярдного стола, но вместо шаров рассматриваются квантовые частицы, поведение которых описывается волновой функцией. Благодаря строго контролируемым параметрам, таким как форма ограничивающей области и энергия частицы, квантовые бильярды позволяют изучать, как незначительные изменения в классической системе могут привести к радикальным изменениям в квантовом поведении, выявляя закономерности, лежащие в основе хаоса и порядка. Исследования в этой области не только углубляют понимание фундаментальных принципов квантовой механики, но и имеют потенциальное применение в разработке новых квантовых устройств и технологий.
Характер классической динамики оказывает определяющее влияние на квантовое поведение системы, что особенно заметно при исследовании квантовых бильярдов. В интегрируемых системах, где траектории частиц предсказуемы и не пересекаются, квантовые состояния проявляют регулярную структуру, характеризующуюся четко выраженными уровнями энергии и волновыми функциями. В отличие от этого, в хаотичных системах, где даже небольшое изменение начальных условий приводит к радикальным изменениям в траектории, квантовые состояния демонстрируют совершенно иную картину — уровни энергии распределены случайным образом, а волновые функции сложны и фрагментированы. Такая связь между классическим хаосом и квантовыми характеристиками позволяет использовать квантовые бильярды в качестве модельных систем для изучения фундаментальных аспектов квантовой механики и перехода от предсказуемого к хаотичному поведению в физических системах.
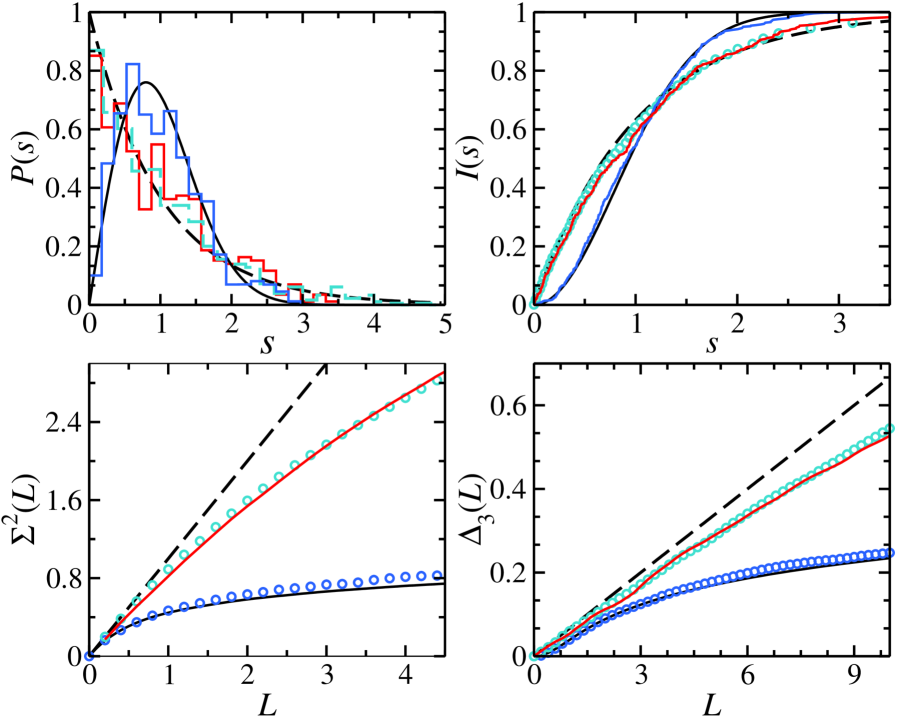
Полусфера как испытательный полигон: интегрируемость и управление
Полусферический квантовый бильярд представляет собой уникальную платформу для исследований благодаря тому, что его классический аналог демонстрирует совершенную интегрируемость. В классической механике, интегрируемая система характеризуется наличием достаточного количества независимых интегралов движения, что позволяет предсказать её эволюцию во времени с высокой точностью. В частности, для полусферы, эти интегралы движения связаны с сохранением энергии и углового момента, что приводит к регулярным траекториям частиц и отсутствию хаотического поведения. Именно эта предсказуемость классического аналога позволяет проводить детальное теоретическое описание квантовой системы и сравнивать результаты с экспериментальными данными, что важно для изучения перехода от интегрируемой к хаотической динамики.
Реализация полусферического квантового бильярда в лабораторных условиях осуществляется посредством прецизионного изготовления физического микроволнового резонатора. Геометрия резонатора, определяющая траектории квантовых частиц, контролируется на этапе производства, что позволяет создать систему с заданными параметрами. Используемые технологии позволяют добиться высокой точности формы и размеров резонатора, обеспечивая соответствие теоретическим моделям и возможность воспроизведения интегрируемой динамики, характерной для классического полусферического бильярда. Конструкция резонатора обеспечивает возможность дальнейшей модификации геометрии и введения параметров, управляющих степенью интеграбельности системы.
Возможность точной настройки параметров системы, в частности посредством “щелевого спаривания” (slit coupling), позволяет исследовать влияние отклонений от полной интегрируемости на квантовое поведение. В ходе экспериментов использовались три уровня спаривания, характеризующиеся соответствующими параметрами: 0.03 — слабое спаривание, 0.23 — умеренное спаривание, и 0.35 — сильное спаривание. Изменение этих параметров позволяет контролировать степень нарушения интегрируемости системы и наблюдать за соответствующими изменениями в квантовой динамике, что дает возможность изучать переход от регулярного к хаотическому поведению.

Расшифровка хаоса: статистические сигнатуры и RMT
Теория случайных матриц (РМТ) предоставляет эффективный инструмент для предсказания статистических свойств квантовых систем, демонстрирующих хаотическое поведение. В основе РМТ лежит предположение о том, что энергетические уровни хаотической системы могут быть смоделированы как собственные значения случайных матриц. Это позволяет вычислять статистические распределения, такие как распределение расстояний между соседними уровнями, дисперсию числа уровней в заданном интервале, и жесткость спектра. Согласие экспериментальных данных с предсказаниями РМТ служит сильным аргументом в пользу хаотического характера системы. β-параметр, используемый в некоторых ансамблях случайных матриц, описывает статистические свойства собственных значений и зависит от симметрий системы (например, унитарные, ортогональные или симплектические).
Для количественной оценки отклонений от предсказаний теории случайных матриц (RMT) и выявления хаотического поведения в квантовых системах используются ключевые метрики, такие как распределение расстояний между ближайшими соседними уровнями энергии (Nearest-Neighbor Spacing Distribution), дисперсия числа уровней в заданном интервале ( \sigma^2 ) и жесткость (Rigidity). Распределение расстояний между уровнями в хаотических системах характеризуется так называемым «репульсивным» законом, в то время как в интегрируемых системах наблюдается иной характер распределения. Дисперсия числа уровней и жесткость отражают статистические свойства спектра энергий и позволяют более детально характеризовать отклонения от предсказаний RMT. Анализ этих метрик позволяет определить, насколько система соответствует предсказаниям RMT, и, следовательно, выявить наличие или отсутствие хаотического поведения.
Согласно гипотезе Берри-Табора, для интегрируемых систем спектральные характеристики проявляют специфическое статистическое поведение, отличное от предсказаний теории случайных матриц (RMT), применимых к хаотическим системам. В частности, для интегрируемых систем ожидается, что распределение расстояний между соседними энергетическими уровнями будет следовать степенному закону, в то время как RMT предсказывает логарифмическое распределение для хаотических систем. Это различие проявляется в метриках, таких как статистическая функция \Delta_3 (Number Variance), которая для интегрируемых систем стремится к нулю, в то время как для хаотических систем она имеет конечное значение, предсказанное RMT. Таким образом, анализ спектральных свойств позволяет дифференцировать интегрируемые и хаотические системы на основе их статистического поведения.
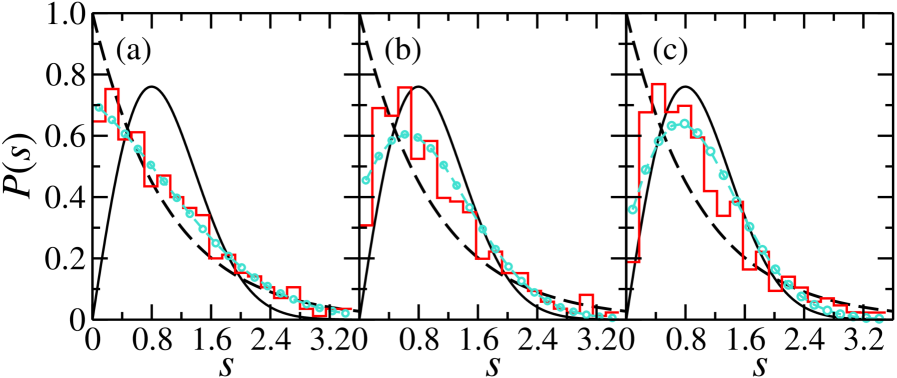
Моделирование и реализация квантового хаоса
Для точного моделирования и оптимизации микроволнового резонатора, используемого в исследованиях квантического хаоса, критически важна роль специализированного программного обеспечения, такого как COMSOL Multiphysics. Данное программное обеспечение позволяет детально проектировать геометрию резонатора, учитывая сложные электромагнитные взаимодействия и граничные условия. С его помощью исследователи могут численно решать уравнения Максвелла, предсказывая распределение электромагнитных волн внутри резонатора и оптимизируя его параметры для достижения требуемых характеристик. Точность моделирования, обеспечиваемая COMSOL Multiphysics, является ключевым фактором в сопоставлении теоретических предсказаний с экспериментальными данными, позволяя изучать тонкие проявления квантического хаоса и проверять справедливость теоретических моделей, таких как предсказания теории случайных матриц RMT и гипотезы Берри-Табора.
Гауссовский ортогональный ансамбль (GOE) представляет собой мощный математический инструмент для анализа квантовых систем, характеризующихся симметрией относительно обращения времени. В экспериментах, посвященных исследованию хаотичных квантовых бильярдов, GOE оказался особенно подходящей моделью, поскольку описывает статистические свойства энергетических уровней систем, где отсутствует внешнее магнитное поле и другие возмущения, нарушающие эту симметрию. Использование GOE позволяет предсказывать распределение расстояний между соседними энергетическими уровнями и другие спектральные характеристики, что, в свою очередь, дает возможность проверить теоретические предсказания и получить более глубокое понимание квантического хаоса. Соответствие экспериментальных данных, полученных в бильярдных системах, предсказаниям GOE подтверждает, что данная статистическая модель адекватно описывает поведение квантовых систем с симметрией относительно обращения времени и является важным этапом в изучении перехода от упорядоченного к хаотическому поведению в квантовой механике.
Исследования показали, что даже слабое взаимодействие между квантовыми бильярдами, демонстрирующими интегрируемое и хаотическое поведение, оказывает измеримое влияние на их спектральные характеристики. Сравнение результатов численного моделирования и экспериментальных данных с предсказаниями теории случайных матриц (RMT) и гипотезы Берри-Табора подтверждает возможность наблюдения этого влияния. Полученные результаты позволяют более глубоко понять переход от упорядоченного к хаотическому поведению в квантовых системах, а также валидировать теоретические модели, описывающие данное явление. Таким образом, даже незначительные возмущения способны существенно изменить энергетический спектр системы, что подчеркивает чувствительность квантовых систем к внешним воздействиям и важность точного учета этих факторов при моделировании и интерпретации экспериментальных данных.
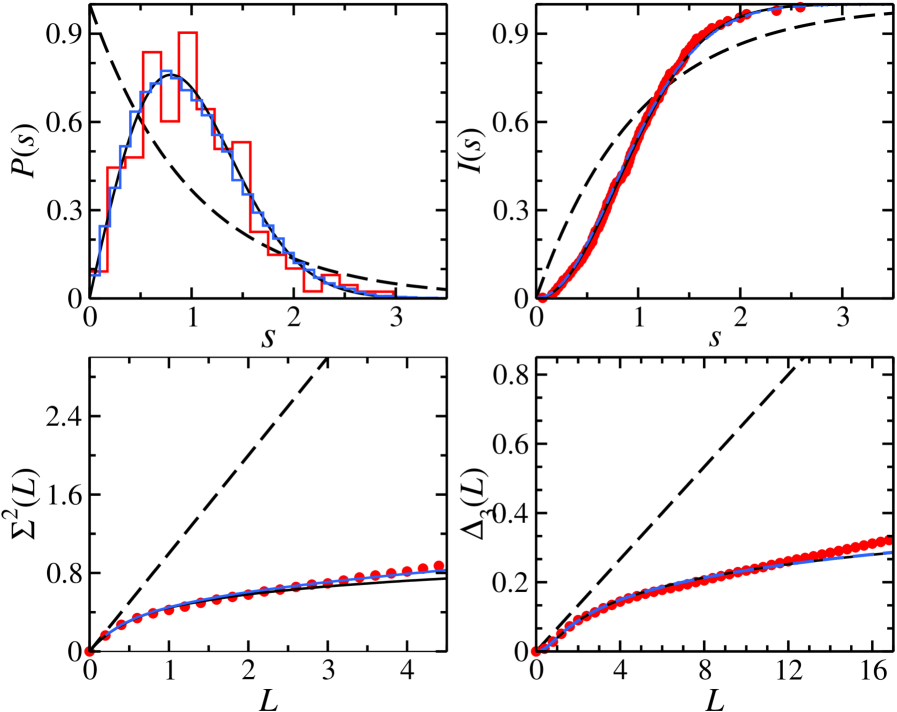
За пределами полусферы: будущие направления в квантовом хаосе
Модель Розенцвейга-Портера представляет собой важный инструмент для изучения систем, демонстрирующих смешанную динамику — сочетание регулярного и хаотического поведения. В отличие от более простых моделей, рассматривающих исключительно хаотичные или регулярные системы, данная модель позволяет исследовать переходные режимы и сложные взаимосвязи между этими двумя типами динамики. Она основана на случайных матрицах, обладающих определенной структурой, что позволяет описывать широкий спектр физических систем, от ядерных реакций до квантовых цепей. Благодаря этому, модель предоставляет теоретическую основу для понимания того, как хаос влияет на квантовые процессы и открывает возможности для управления этими процессами. Использование данной модели существенно расширяет границы исследований в области квантического хаоса, позволяя анализировать системы, которые ранее оставались за пределами досягаемости традиционных подходов.
Исследование влияния различных симметрий, в частности, описываемых Гауссовым Симплектическим Ансамблем (GSE), открывает новые горизонты в понимании квантового хаоса. GSE представляет собой математическую модель, позволяющую учитывать сложные взаимосвязи между квантовыми системами, обладающими определенной симметрией. Анализ систем, соответствующих GSE, демонстрирует, что характерные признаки квантового хаоса — такие как уровень отталкивания и статистические закономерности в спектре энергии — существенно зависят от типа симметрии. Изучение этих зависимостей позволяет более точно описывать поведение сложных квантовых систем, находящихся в условиях хаотической динамики, и, как следствие, получать более полную картину квантового хаоса, выходящую за рамки традиционных подходов.
Полученные знания о квантическом хаосе находят применение в самых различных областях науки и техники. В ядерной физике, понимание хаотических процессов позволяет более точно моделировать структуру и поведение атомных ядер, что важно для разработки новых источников энергии и методов диагностики. В области квантовой информатики, принципы квантического хаоса используются для создания более надежных и эффективных алгоритмов, а также для разработки новых методов квантового шифрования. Более того, исследования в данной области способствуют созданию новых материалов с уникальными свойствами, открывая перспективы для разработки инновационных технологий в сфере сенсорики и обработки информации. Таким образом, углубленное изучение квантического хаоса не только расширяет границы фундаментальных знаний, но и создает платформу для технологических прорывов в будущем.
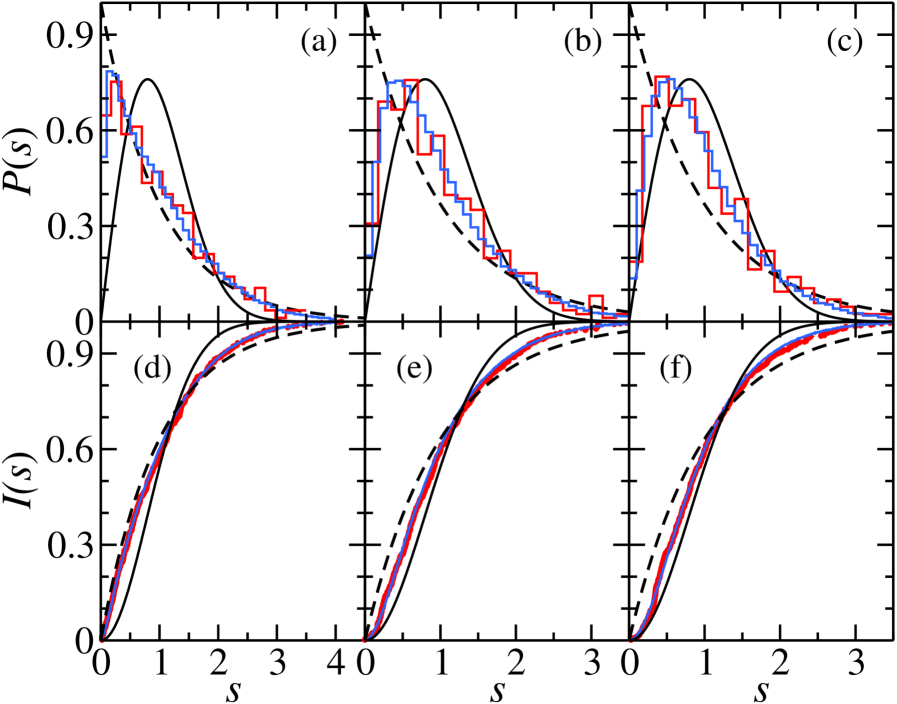
Исследование, посвященное спектральным свойствам связанных квантовых бильярдов, подчеркивает, насколько даже слабое взаимодействие между упорядоченными и хаотичными системами способно изменить характеристики спектра. Это демонстрирует, что автоматизация без учета возможных последствий может привести к непредскануемым результатам. Как отмечал Фрэнсис Бэкон: «Знание — сила», однако эта сила должна быть направлена на благо, а не просто на достижение технических целей. Понимание влияния взаимодействия систем, особенно в контексте хаоса и порядка, требует от исследователей не только математической точности, но и этической ответственности за моделируемые процессы и их потенциальное влияние.
Куда двигаться дальше?
Представленное исследование, демонстрирующее влияние даже слабого взаимодействия между интегрируемыми и хаотическими квантовыми системами на спектральные характеристики, поднимает вопрос о границах применимости существующих теоретических моделей. Несмотря на успех модифицированной модели Розенцвейга-Портера в описании наблюдаемых эффектов, остаётся неясным, насколько универсальна эта модель для более сложных конфигураций взаимодействующих систем. В конце концов, каждая попытка упростить реальность, даже с помощью элегантного математического аппарата, неизбежно несёт в себе определённые упрощения и, следовательно, ограничения.
Перспективы дальнейших исследований лежат, вероятно, в направлении изучения влияния топологии взаимодействующих систем на их спектральные свойства. Необходимо исследовать, как изменения в геометрии «квантовых бассейнов» и характере их связи влияют на наблюдаемые закономерности. Важно также учитывать, что любой алгоритм, используемый для анализа спектральных данных, кодирует определённые предположения о природе системы, и эти предположения должны быть тщательно проанализированы и, по возможности, проверены экспериментально.
В конечном счете, прогресс в данной области требует не только разработки более точных математических моделей, но и осознания этической ответственности исследователя. Каждый выбор алгоритма имеет социальный контекст, и только осознанная разработка минимизирует вред. Иначе, увлечение техническими деталями может затмить более важные вопросы о природе реальности и месте человека в ней.
Оригинал статьи: https://arxiv.org/pdf/2601.11212.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Все рецепты культистского круга в Escape from Tarkov
- Решение головоломки с паролем Absolum в Yeldrim.
- Лучшие транспортные средства в Far Cry 6
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Репозиторий: Как исправить таймаут клиента
- Кто такая Кселия Мендес-Джонс? 5 вещей, которые нужно знать об актере Fallout
- Лучшие колоды в рейтинге Clash Royale (июль 2025)
- Акции привилегированные TATNP. Татнефть: прогноз акций привилегированных.
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Прогнозы криптовалюты XVG: информация о ценах на XVG
2026-01-19 10:56