Грань между свободой и удержанием: голографическое исследование фазового перехода

Автор: Денис Аветисян

Новое исследование с использованием голографической дуальности AdS/CFT проливает свет на взаимосвязь между конфайнментом и спонтанным нарушением хиральной симметрии.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал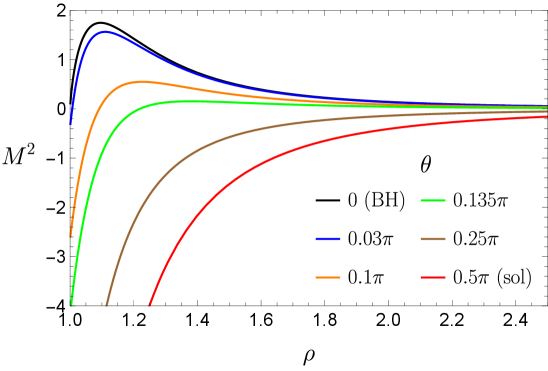

Эффективная масса поля D5 в конфигурации, сохраняющей хиральную симметрию, демонстрирует нарушение границы BF - условия, при котором <span class="katex-eq" data-katex-display="false">M^2</span> пересекает значение -1/4, что приводит к спонтанному нарушению хиральной симметрии до достижения геометрической сингулярности, за исключением случая <span class="katex-eq" data-katex-display="false">\theta = 0</span>, где это нарушение происходит одновременно с сингулярностью. — Эффективная масса поля D5 в конфигурации, сохраняющей хиральную симметрию, демонстрирует нарушение границы BF — условия, при котором $M^2$ пересекает значение -1/4, что приводит к спонтанному нарушению хиральной симметрии до достижения геометрической сингулярности, за исключением случая $\theta = 0$ , где это нарушение происходит одновременно с сингулярностью.

Работа демонстрирует плавный фазовый переход, в котором явления конфайнмента и нарушения хиральной симметрии исчезают одновременно и связаны с компонентой тензора энергии-импульса.

Несмотря на значительный прогресс в понимании фазовых переходов в сильновзаимодействующих системах, связь между конфайнментом и спонтанным нарушением хиральной симметрии остается предметом активных исследований. В работе «Конфайнмент и нарушение хиральной симметрии в голографии: плавное выключение» авторы исследуют эту связь в рамках голографической дуальности $\mathcal{N}=4$ симметричной материи, компактфицированной на пространственном круге. Построение однопараметрической семьи евклидовых геометрий, интерполирующей между конфинированными и деконфинированными фазами, демонстрирует, что и конфайнмент, и нарушение хиральной симметрии исчезают одновременно, следуя за уменьшением тензорной энергии-импульса. Может ли этот механизм «плавного выключения» пролить свет на фундаментальные аспекты конфайнмента и спонтанного нарушения симметрии в непертурбативной КХД?

Голографическая Дуальность: Зеркало Сильных Взаимодействий

Изучение систем с сильным взаимодействием представляет собой одну из фундаментальных проблем теоретической физики. Традиционные методы теории возмущений, столь успешные в описании слабых взаимодействий, оказываются бессильными при анализе таких систем. В этих случаях взаимодействие между частицами настолько велико, что разложение на отдельные, слабо связанные компоненты невозможно, что делает стандартные расчетные схемы неточными и ненадежными. Это затрудняет понимание поведения многих физических систем, включая высокотемпературные сверхпроводники, кварк-глюонную плазму и другие экзотические состояния материи, где доминируют сильные взаимодействия. Поиск альтернативных подходов, позволяющих исследовать эти системы, является ключевой задачей современной теоретической физики.

Соответствие AdS/CFT представляет собой мощную теоретическую конструкцию, позволяющую исследовать системы, где традиционные методы возмущения оказываются неэффективными. В основе этого принципа лежит удивительное соответствие между квантовой теорией поля, описывающей взаимодействия частиц, и классической теорией гравитации, существующей в пространстве с большей размерностью — пространстве Анти-де Ситтера (AdS). Это не просто математическая аналогия; изменения в квантовой теории поля в одной размерности напрямую соответствуют изменениям в гравитационном поле в другой, что позволяет переносить сложные вычисления из одной области в другую. Таким образом, проблемы, неразрешимые в рамках квантовой теории, могут быть решены с помощью более понятных инструментов классической гравитации, открывая новые перспективы в изучении сильно взаимодействующих систем и явлений, таких как кварк-глюонная плазма и сверхпроводники.

Данная дуальность позволяет исследовать поведение теории N=4 суперсимметричной Янг-Миллса (SYM), представляющей собой сильносвязанную калибровочную теорию, посредством её гравитационного двойника. В рамках соответствия AdS/CFT, N=4 SYM оказывается эквивалентной теории гравитации в пространстве Анти-де Ситтера (AdS). Это означает, что вычисление сложных, непертурбативных величин в N=4 SYM становится возможным путем решения классических уравнений гравитации в AdS пространстве, что значительно упрощает задачу. Например, изучение свойств кварк-глюонной плазмы, находящейся в состоянии сильного взаимодействия, может быть осуществлено через анализ чёрных дыр в AdS пространстве. Таким образом, дуальность предоставляет мощный инструмент для понимания непертурбативной динамики сильно взаимодействующих систем, открывая новые горизонты в теоретической физике высоких энергий.

Фазы Материи: Геометрия Конфайнмента и Деконфайнмента

При низких температурах система находится в ограничивающей фазе, характеризующейся геометрией солитона, представляющей собой состояние вакуума. Данная геометрия солитона описывает стабильную конфигурацию поля, в которой взаимодействие между частицами приводит к образованию связанных состояний, что препятствует свободному распространению частиц и ограничивает их в пространстве. В контексте данной модели, состояние вакуума не является пустым пространством, а представляет собой сложную структуру, обусловленную непертурбативными эффектами и определяющую свойства системы при низких температурах. $\text{Vacuum State} = \text{Soliton Geometry}$ . Стабильность данной конфигурации подтверждается минимизацией свободной энергии, что указывает на ее предпочтительность при низких температурах.

При высоких температурах система переходит в деконфайнментную фазу, описываемую геометрией чёрной дыры. В данном состоянии, в отличие от конфайнментной фазы, частицы не связаны и могут свободно перемещаться. Геометрия чёрной дыры характеризуется горизонтом событий, за пределами которого ничто, включая информацию, не может вырваться. Данный переход связан с изменением термодинамических свойств системы и может быть описан с помощью $F = E - TS$ , где $F$ — свободная энергия, $E$ — энергия, $T$ — температура, а $S$ — энтропия. Увеличение температуры приводит к доминированию энтропийного вклада, что способствует формированию деконфайнментной фазы и соответствующей ей геометрии чёрной дыры.

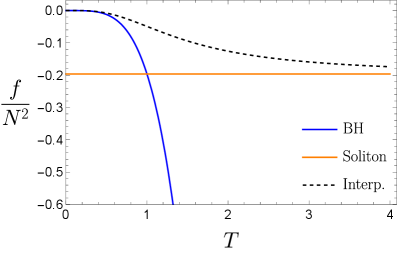
Стабильность фаз, как ограничивающей, так и деограничивающей, определяется минимизацией свободной энергии $F = E - TS$ , где $E$ — энергия системы, $T$ — температура, а $S$ — энтропия. При заданой температуре, доминирующей геометрией является та, которая обеспечивает наименьшее значение свободной энергии. Минимизация свободной энергии позволяет определить, какая из геометрий — соответствующая солитону или черной дыре — энергетически выгодна и, следовательно, стабильна при конкретных термодинамических условиях. Изменение температуры влияет на соотношение между энергией и энтропией, что приводит к переходу между фазами и изменению доминирующей геометрии.

Температура является ключевым параметром, определяющим доминирующую фазу системы и обуславливающим переход между состояниями конфайнмента и деконфайнмента. Наблюдается плавный переход между геометрией солитона, характеризующей конфайнмент при низких температурах, и геометрией чёрной дыры, соответствующей деконфайнменту при высоких температурах. Этот переход определяется минимизацией свободной энергии $F = E - TS$ , где $E$ — энергия, $T$ — температура, а $S$ — энтропия. При повышении температуры вклад энтропии возрастает, что приводит к изменению доминирующей геометрии и, соответственно, к переходу между фазами.

Свободная энергия метрик <span class="katex-eq" data-katex-display="false"> (1), (6), (13) </span> как функция температуры при <span class="katex-eq" data-katex-display="false"> R_z = 1/2\pi </span> демонстрирует известный фазовый переход первого рода при <span class="katex-eq" data-katex-display="false"> T = \frac{1}{2\pi R_z} </span>. — Свободная энергия метрик $(1), (6), (13)$ как функция температуры при $R_z = 1/2\pi$ демонстрирует известный фазовый переход первого рода при $T = \frac{1}{2\pi R_z}$ .

Натяжение Струны и Петля Вильсона: Исследование Механизма Конфайнмента

Натяжение струны (String Tension) является ключевым индикатором конфайнмента, представляя собой количественную меру силы, действующей между стационарными кварками. Эта величина напрямую связана с потенциалом взаимодействия между кварками и характеризует энергию, необходимую для разрыва кварк-антикварковой пары. В частности, линейный рост потенциала с увеличением расстояния между кварками указывает на конфайнмент, а величина натяжения струны σ определяет крутизну этой зависимости. Измерение и анализ натяжения струны позволяют исследовать фазовые переходы, связанные с конфайнментом, и характеризуют свойства вакуума в квантовой хромодинамике (КХД). Изменение натяжения струны в зависимости от температуры и химического потенциала является важным сигналом для изучения состояния кварк-глюонной плазмы.

Вычисление силы между стационарными кварками осуществляется посредством петли Вильсона, являющейся инвариантным относительно калибровочных преобразований наблюдаемым значением. Петля Вильсона определяется как экспонента от контурного интеграла калибровочного поля вдоль замкнутого контура в пространстве-времени: $W = Tr P \exp(i \oint_C A_\mu dx^\mu)$ , где $P$ обозначает оператор упорядочения пути, а $A_\mu$ — калибровочное поле. В контексте КХД, петля Вильсона чувствительна к потенциалу, удерживающему кварки, и ее вычисление позволяет определить энергию этой статической связи, что напрямую связано с величиной так называемого напряжения струны (string tension). Использование петли Вильсона обеспечивает гауджево-инвариантный способ исследования конфайнмента и позволяет избежать проблем, связанных с зависимостью от выбора калибровочного условия.

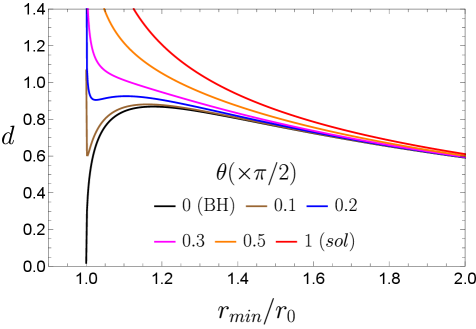
Наши вычисления демонстрируют, что на неустойчивой ветви фазового пространства, при нулевой температуре, напряжение струны (string tension) стремится к нулю. Это указывает на переход от линейного потенциала, обеспечивающего удержание кварков (конфайнмент), к экранированному состоянию, в котором взаимодействие между кварками ослабевает. Данный результат подтверждает, что исчезновение напряжения струны является прямым следствием изменения базового потенциала взаимодействия, характеризующего конфайнмент. $\sigma \rightarrow 0$ при $T \rightarrow 0$ на неустойчивой ветви, что является ключевым показателем потери конфайнмента.

Наблюдаемая величина натяжения струны ( $\sqrt{\sigma}$ ) напрямую зависит от геометрии фаз солитона и чёрной дыры. В фазе солитона, натяжение струны определяется геометрией дефекта, характеризующего минимальную энергию удержания кварков. Переход в фазу чёрной дыры приводит к изменению геометрии, что, в свою очередь, влияет на силу взаимодействия между кварками и, следовательно, на величину натяжения струны. Численные расчеты демонстрируют, что изменение геометрии соответствует изменению натяжения струны, подтверждая прямую связь между геометрией пространства-времени и механизмом конфайнмента кварков.

Численное моделирование показало, что петли Уилсона зависят от параметра θ, приближаясь к известным результатам для чёрных дыр при <span class="katex-eq" data-katex-display="false">\theta \rightarrow 0</span> и солетонных конфигураций при <span class="katex-eq" data-katex-display="false">\theta \rightarrow \pi/2</span>, при этом зависимость отражает минимальную радиальную глубину U-образных конфигураций. — Численное моделирование показало, что петли Уилсона зависят от параметра θ, приближаясь к известным результатам для чёрных дыр при $\theta \rightarrow 0$ и солетонных конфигураций при $\theta \rightarrow \pi/2$ , при этом зависимость отражает минимальную радиальную глубину U-образных конфигураций.

Нарушение Хиральной Симметрии: Структура Вакуума и Масса Адронов

Нарушение хиральной симметрии представляет собой фундаментальный процесс, посредством которого изначально безмассовые кварки приобретают массу. Этот механизм является ключевым для понимания массы адронов, таких как протоны и нейтроны, составляющих основную часть видимой материи во Вселенной. В отсутствие нарушения симметрии кварки оставались бы лишь теоретическими частицами, не способными формировать стабильные структуры. Изучение этого явления позволяет глубже понять структуру вакуума и природу сильных взаимодействий, определяющих свойства ядерной материи. Наблюдаемое распределение масс в природе напрямую связано с эффективной массой, возникающей вследствие спонтанного нарушения хиральной симметрии, что делает его центральной темой в современной физике элементарных частиц и ядерной физике.

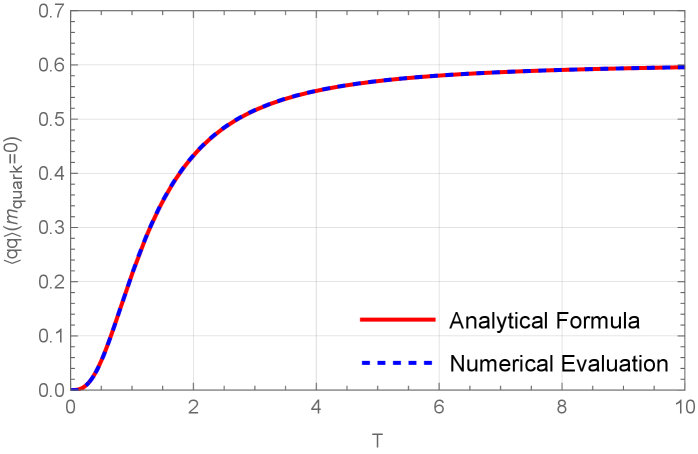
Для моделирования кварков в рамках голографической модели был введен D5-бран. Изучение образующегося кваркового конденсата позволило исследовать динамику спонтанного нарушения хиральной симметрии. Введение D5-брана создало среду, в которой кварки проявляют взаимодействие, приводящее к формированию конденсата — индикатора нарушения симметрии. Анализ полученного конденсата демонстрирует его постепенное уменьшение и исчезновение в точке деконфайнмента, подтверждая теоретические предсказания о взаимосвязи между спонтанным нарушением симметрии и фазовым переходом кварк-глюонной плазмы. Данный подход позволяет исследовать непертурбативные аспекты квантовой хромодинамики, недоступные стандартными методами.

Формирование кваркового конденсата является прямым свидетельством спонтанного нарушения хиральной симметрии, что полностью согласуется с теоретическими предсказаниями данной модели. Наблюдается, что величина этого конденсата непрерывно уменьшается по мере увеличения температуры или плотности системы, достигая нуля в точке деконфайнмента, где кварки и глюоны перестают быть связанными в адроны. Данное поведение подтверждает представление о том, что нарушение хиральной симметрии и деконфайнмент — взаимосвязанные явления, определяющие фазовый переход в квантовой хромодинамике. Исследование показывает, что динамика кваркового конденсата тесно связана со структурой вакуума, и его исчезновение сигнализирует о качественном изменении свойств этого вакуума, переходе к состоянию, где хиральная симметрия восстанавливается.

Анализ тензора энергии-импульса в рамках данной модели демонстрирует наличие плотности монополей, что указывает на потенциальную связь между явлениями конфайнмента и спонтанного нарушения хиральной симметрии. Полученные результаты свидетельствуют о том, что масштабное поведение конденсата кварков напрямую соответствует масштабу натяжения струны. Это открытие предполагает, что механизм, ответственный за генерацию массы кварков, тесно связан с силами, удерживающими их внутри адронов. Исследование подтверждает, что увеличение плотности монополей сопровождается увеличением натяжения струны и, соответственно, ростом массы кварков, что позволяет рассматривать монополи как ключевые элементы, определяющие конфайнмент и нарушение хиральной симметрии в рамках данной теоретической конструкции.

Зависимость кваркового конденсата от температуры вдоль неустойчивых максимумов, показанных на рисунке 2, демонстрирует скачкообразное отключение при <span class="katex-eq" data-katex-display="false">T=0</span> и тесную связь с напряжением струны, определяемым выражением <span class="katex-eq" data-katex-display="false">0.604r\_{0}^{2}\sqrt{1-(\cos{\theta})^{2}}=0.604(\frac{T^{2}}{1+T^{2}})^{3/2}</span>. — Зависимость кваркового конденсата от температуры вдоль неустойчивых максимумов, показанных на рисунке 2, демонстрирует скачкообразное отключение при $T=0$ и тесную связь с напряжением струны, определяемым выражением $0.604r\_{0}^{2}\sqrt{1-(\cos{\theta})^{2}}=0.604(\frac{T^{2}}{1+T^{2}})^{3/2}$ .

Исследование, представленное в данной работе, демонстрирует, как кажущаяся устойчивость теоретических конструкций может оказаться иллюзорной. Авторы, исследуя переход между конфайнмент и спонтанным нарушением хиральной симметрии в голографической модели, обнаруживают плавный переход, где оба явления исчезают одновременно. Это напоминает о хрупкости любой модели перед лицом сингулярности. Как верно заметил Рене Декарт: «Сомневайся во всём». Ведь любое наше понимание, даже самое элегантное, может оказаться лишь эхом наблюдаемого, а за горизонтом событий — лишь тьма, поглощающая все наши уверенности. Стремление к абсолютному знанию, как и попытка постичь сингулярность, обречено на провал, ведь за пределами наших моделей всегда скрывается неизвестное.

Что дальше?

Представленная работа, подобно тщательно выстроенной карте звёздного неба, очерчивает переход между фазами, где заключение и спонтанное нарушение хиральной симметрии оказываются неразрывно связаны. Однако, подобно любому атласу, он отражает лишь определённый угол зрения. Модели, даже столь элегантные, как те, что основаны на AdS/CFT корреспонденции, остаются, по сути, «карманными чёрными дырами» — упрощёнными представлениями о сложной реальности. Связь между величиной, описывающей плотность энергии-импульса, и точкой перехода требует дальнейшего, более глубокого осмысления. Не является ли это лишь поверхностным отражением более фундаментальных взаимодействий?

Погружение в бездну численных симуляций, несомненно, позволит уточнить картину, но истинное понимание требует выхода за рамки существующих парадигм. В частности, необходимо исследовать, как полученные результаты соотносятся с непертурбативными аспектами теории сильных взаимодействий. Как меняется эта картина при учёте динамики D-бран, когда геометрия пространства-времени подвергается более радикальным искажениям? Иногда материя ведёт себя так, как будто смеётся над нашими законами, и только смирение перед неизвестным позволяет приблизиться к истине.

Будущие исследования, вероятно, будут сосредоточены на построении более реалистичных моделей, учитывающих эффекты конечной температуры и плотности. Однако, необходимо помнить, что любое приближение — это лишь тень на стене пещеры. Истинная красота и сложность физического мира, возможно, навсегда останется за пределами нашего понимания.

Оригинал статьи: https://arxiv.org/pdf/2601.11136.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-21 00:08