Автор: Денис Аветисян
Новое исследование показывает, что сам процесс измерения влияет на статистику первого обнаружения квантовой частицы, приводя к неожиданному переходу от экспоненциального к степенному затуханию.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал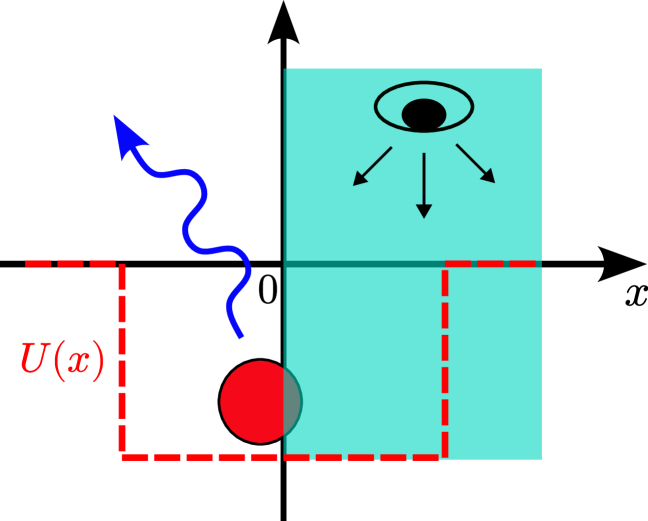
Исследование влияния квантовых измерений на время первого обнаружения частицы в потенциальной яме и зависимость от энергетического спектра.
В классической теории первого прохода время достижения системой определенного состояния считается независимым от процесса наблюдения. В данной работе, посвященной ‘Measurement-induced crossover in quantum first-detection times’, исследуется влияние повторяющихся квантовых измерений на статистику первого обнаружения частицы в заданном состоянии. Показано, что характер распада вероятности первого обнаружения меняется от экспоненциального в случае наличия ограничивающего потенциала к алгебраическому для свободной частицы, причём наблюдается переход между этими режимами в зависимости от спектра энергии. Может ли подобный переход служить индикатором чисто квантовой природы процесса обнаружения и принципиально ли он отличается от классической задачи о первом проходе?
За гранью классических представлений: Квантовое первое прохождение
Традиционные методы статистики первого прохождения, широко применяемые для описания времени, необходимого частице для достижения определенной границы, базируются на представлении о классических траекториях движения. Однако, в масштабах, где доминируют квантовые эффекты, такое упрощение становится неприменимым. В этих условиях частица не следует четко определенной траектории, а описывается волновой функцией, что приводит к вероятностному характеру ее движения и существенным отклонениям от классических предсказаний. Игнорирование квантовой природы частицы в этих случаях может привести к неверной оценке времени первого прохождения и, как следствие, к ошибочным выводам в различных областях, начиная от изучения химических реакций и заканчивая анализом электронного транспорта в наноматериалах. Понимание влияния квантовых эффектов на статистику первого прохождения становится ключевым для разработки точных моделей и предсказаний в микро- и нано-мире.
Понимание того, как квантовая частица впервые достигает границы потенциального барьера, является основополагающим для множества областей науки и техники. В химии, это напрямую связано со скоростью протекания химических реакций, поскольку частицы должны преодолеть энергетический барьер для превращения в продукты. В физике твердого тела, этот процесс играет ключевую роль в понимании электронного транспорта в наноматериалах и полупроводниковых приборах, определяя скорость и эффективность проводимости. Более того, принципы, лежащие в основе этого явления, применимы к моделированию биологических процессов, таких как диффузия молекул через клеточные мембраны, и даже к пониманию ранних этапов формирования Вселенной. Изучение момента первого достижения границы позволяет более точно описывать и прогнозировать поведение квантовых систем в различных условиях, открывая новые возможности для разработки инновационных технологий и материалов.
Исследование посвящено изучению влияния непрерывных квантовых измерений на время первого достижения границы частицей, выявляя существенные отклонения от классических предсказаний. В рамках работы показано, что постоянный процесс измерения, взаимодействуя с квантовой системой, изменяет динамику ее эволюции, приводя к нетривиальным изменениям в распределении времени первого прохождения. Полученные результаты демонстрируют переход от экспоненциального затухания вероятности первого достижения границы, характерного для классических систем, к алгебраическому, обусловленному обратным воздействием измерений. Этот переход указывает на фундаментальную роль квантовых эффектов в процессах, определяемых временем первого достижения, и имеет значение для понимания динамики в различных областях, включая химические реакции и транспорт электронов.
Данное исследование, поддержанное проектом PNRR MUR, направлено на создание надежной теоретической основы для изучения первого прохождения квантовой частицы через границу. В рамках этой работы продемонстрирован переход от экспоненциального к алгебраическому спаду вероятности первого прохождения, обусловленный эффектом обратной связи, возникающим при непрерывном квантовом измерении. Этот переход указывает на то, что традиционные методы, основанные на классических траекториях, становятся неадекватными при описании поведения квантовых систем под воздействием измерений, и требует разработки новых подходов для точного предсказания динамики процессов, таких как химические реакции и транспорт электронов. Результаты работы позволяют глубже понять влияние измерений на квантовую эволюцию и открывают перспективы для создания новых квантовых технологий.
Роль измерения: Формирование квантовой эволюции
Квантовое измерение не является пассивным наблюдением; оно активно воздействует на измеряемую систему посредством эффекта, известного как «обратное действие измерения» (measurement back action). Этот эффект обусловлен тем, что процесс измерения неизбежно вносит возмущение в состояние системы, изменяя её эволюцию. В отличие от классической физики, где измерение предполагается идеальным и не влияющим на объект, в квантовой механике любое измерение приводит к коллапсу волновой функции и переходу системы в одно из собственных состояний оператора измерения. Степень этого возмущения зависит от типа измерения и состояния системы, но всегда присутствует и влияет на последующую динамику системы. Это означает, что наблюдаемая эволюция системы является результатом как её естественной динамики, так и возмущения, вызванного самим процессом измерения.
Для исследования эволюции квантовой частицы используется стробоскопическое измерение, представляющее собой последовательность проективных измерений, выполняемых через определенные интервалы времени. Каждое проективное измерение приводит к коллапсу волновой функции частицы в одно из собственных состояний оператора измерения, после чего начинается новая эволюция, описываемая уравнением Шрёдингера. Повторение этой процедуры позволяет отслеживать изменения состояния частицы во времени, фактически «замораживая» ее эволюцию между измерениями и получая информацию о ее динамике посредством анализа результатов каждого проективного измерения. Частота повторения измерений является ключевым параметром, определяющим режим наблюдения — от режима Зено, где измерения выполняются очень часто, до режима, допускающего значительную эволюцию между измерениями.
Режим Зено, характеризующийся частыми измерениями квантовой системы, приводит к значительному замедлению или даже полной остановке её эволюции. Этот эффект обусловлен тем, что каждое последовательное измерение «сбрасывает» волновой пакет частицы в одно из собственных состояний оператора измерения. Чем чаще производятся измерения, тем меньше времени у частицы для перехода в другое состояние, что эффективно «замораживает» её движение. Математически, вероятность обнаружить частицу в исходном состоянии после n последовательных измерений экспоненциально приближается к единице при увеличении частоты измерений, что подтверждает эффект подавления эволюции в режиме Зено.
В режиме, отличном от эффекта Зено (Non-Zeno), менее частые измерения позволяют квантовой системе эволюционировать в значительной степени между последовательными актами наблюдения. Это приводит к изменению наблюдаемых скоростей распада, поскольку вероятность перехода в другое состояние между измерениями становится существенной. В отличие от режима Зено, где частые измерения «замораживают» систему в исходном состоянии, в режиме Non-Zeno система имеет достаточно времени для проявления своей естественной динамики, что проявляется в ускорении или изменении скорости распада по сравнению с ситуацией, когда измерений не производится. Величина изменения скорости распада зависит от интервала времени между измерениями и характеристик самой квантовой системы.
Аналитический каркас: Картирование квантовой динамики
В режиме Зено применяется метод преобразования к мнимому потенциалу, позволяющий представить сложную эволюцию квантовой системы в виде эквивалентной задачи под действием мнимого потенциала V_{eff} = -iV(x). Данный подход основан на математической эквивалентности между временной эволюцией под действием гамильтониана и стационарной задачей Шрёдингера с модифицированным потенциалом. Преобразование позволяет упростить расчеты, заменяя решение временной зависимости на поиск стационарных состояний, что особенно полезно при анализе динамики в ситуациях, когда система подвергается частым измерениям или взаимодействиям, препятствующим её эволюции.
Применение метода отображения на мнимый потенциал позволяет существенно упростить расчеты, связанные с анализом квантовой динамики в зено-режиме. Преобразование исходной задачи к эквивалентной задаче с мнимым потенциалом приводит к замене временной эволюции на решение стационарного уравнения Шрёдингера с мнимой массой. Это позволяет использовать стандартные методы квантовой механики для исследования динамики, избегая необходимости решать сложное временное уравнение. В частности, анализ спектральных свойств полученного гамильтониана с мнимым потенциалом предоставляет информацию о скорости затухания волновой функции и характере эволюции квантового состояния, что невозможно получить прямым решением исходной задачи.
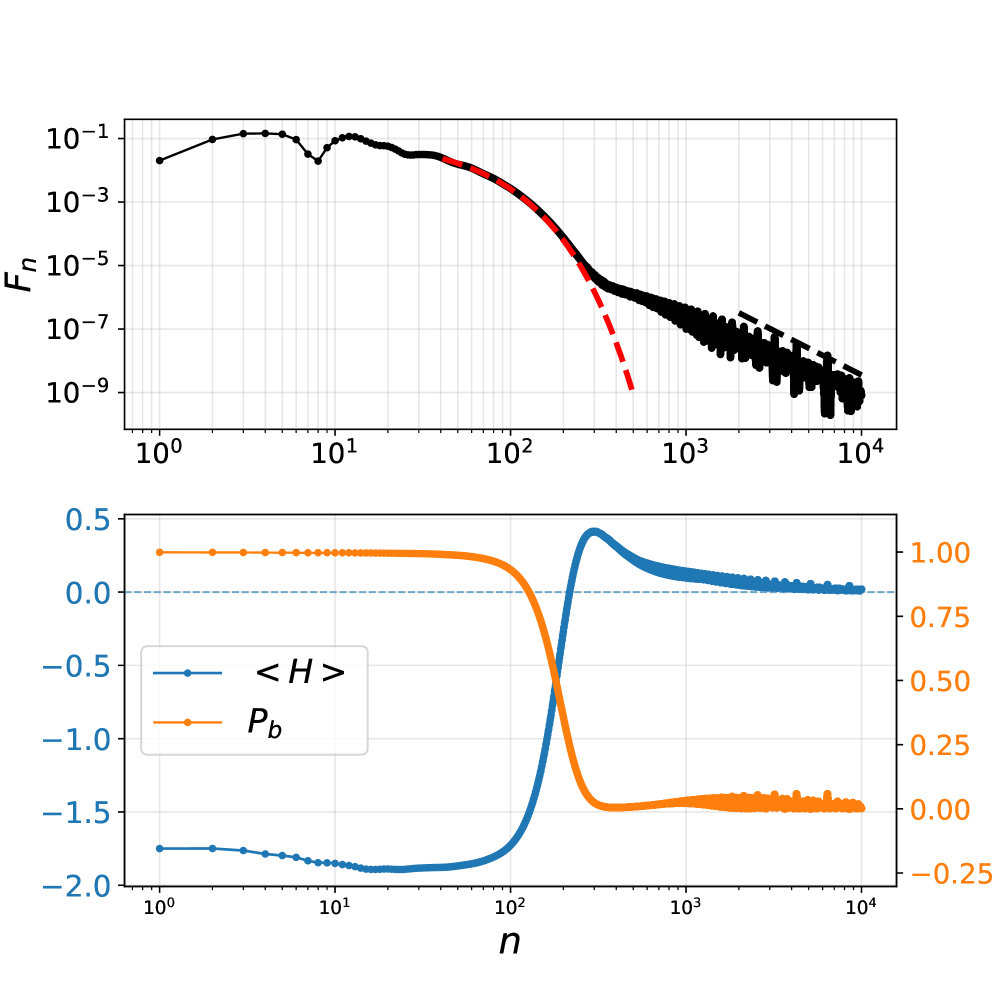
Для анализа динамики в рамках предложенного подхода применяются различные модельные системы. Исследуется динамика свободной частицы, для которой характерно распространение волновой функции без ограничений. Гармонический осциллятор демонстрирует дискретный энергетический спектр и существование связанных состояний. Особое внимание уделяется потенциальной яме, где наблюдается непрерывный спектр и формирование как связанных, так и рассеивающих состояний. Анализ динамики в потенциальной яме выявляет переход от экспоненциального затухания к алгебраическому, с показателем затухания, приблизительно равным 2.8.
Рассмотренные модели — квантовый гармонический осциллятор и потенциальная яма — демонстрируют различные спектральные характеристики. Гармонический осциллятор характеризуется дискретным спектром энергии, приводящим к образованию связанных состояний. В отличие от него, потенциальная яма обладает непрерывным спектром, формирующим рассеянные состояния. При анализе динамики в потенциальной яме наблюдается переход от экспоненциального затухания во времени к алгебраическому, характеризующемуся показателем приблизительно равным 2.8. Данный переход указывает на изменение характера распада волновой функции в исследуемом потенциале.
За пределами экспоненциального спада: Раскрытие новой динамики
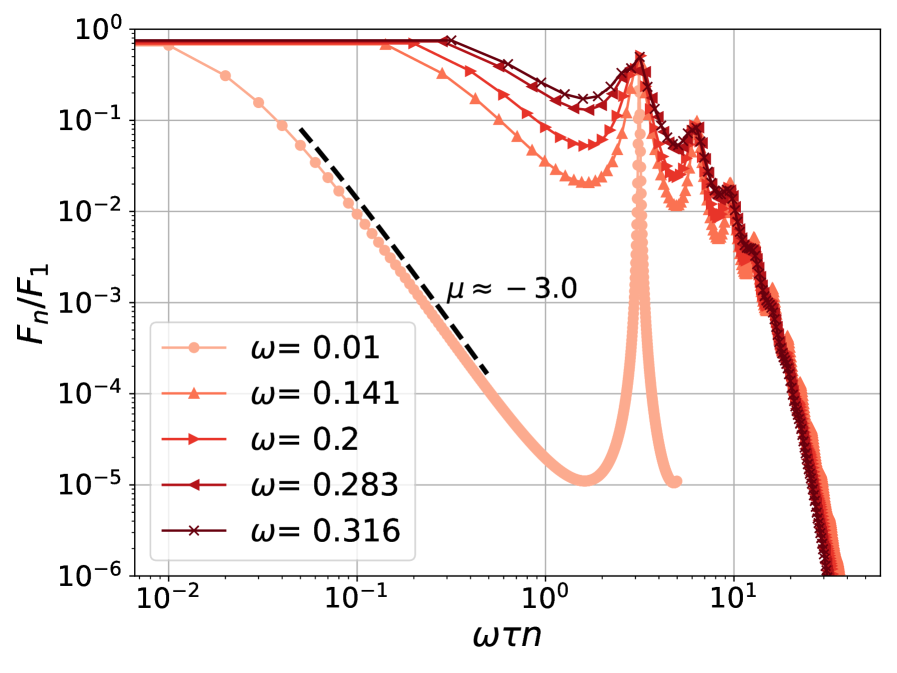
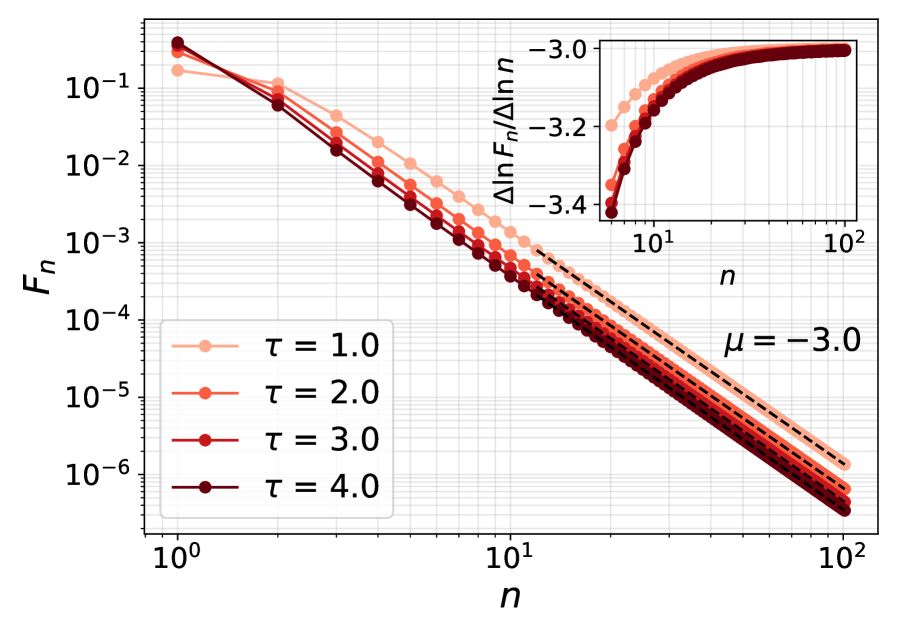
Расчёты демонстрируют, что непрерывное квантовое измерение приводит к отклонениям от привычного экспоненциального затухания, характерного для классических систем. В отличие от классической физики, где вероятность обнаружения частицы уменьшается пропорционально e^{-t/\tau}, в квантовых системах, подвергающихся постоянному измерению, наблюдается иное поведение. Вместо экспоненциального спада, вероятность может убывать по степенному закону — так называемое алгебраическое затухание, особенно выраженное для свободных частиц, где скорость убывания пропорциональна n^{-3}. Более того, скорость экспоненциального затухания, если оно и сохраняется, модифицируется и становится зависимой от частоты проводимых измерений, что указывает на существенное влияние процесса измерения на динамику квантовой системы. Данные отклонения от классической картины открывают новые возможности для управления квантовыми процессами и понимания поведения частиц в условиях постоянного наблюдения.
Исследования показали, что непрерывные квантовые измерения приводят к отклонениям от классического экспоненциального затухания. В частности, для свободной частицы наблюдается так называемое алгебраическое затухание, характеризующееся более медленным спадом, подчиняющимся степенному закону с показателем n^{-3}. При этом, скорость затухания не является фиксированной, а существенно зависит от частоты проводимых измерений. Увеличение частоты измерений приводит к модификации экспоненциальной скорости затухания, что указывает на возможность активного контроля над динамикой квантовой системы посредством частоты и интенсивности измерений. Эти наблюдения демонстрируют, что стандартные модели, основанные на экспоненциальном спаде, могут быть неадекватны для описания квантовых процессов, подвергающихся непрерывным измерениям.
Исследования показали, что эффективный потенциал, индуцированный непрерывным квантовым измерением, обратно пропорционален интервалу времени между измерениями — V_0 \approx 1/\tau. Это означает, что чем чаще производится измерение, тем сильнее становится потенциал, влияющий на эволюцию квантовой системы. Установленная зависимость позволяет напрямую связать характеристики процесса измерения с величиной возмущения, которое оно оказывает на исследуемый объект. Такая связь открывает возможности для целенаправленного управления квантовой динамикой, поскольку позволяет регулировать силу индуцированного потенциала посредством изменения частоты измерений. Полученный результат имеет принципиальное значение для разработки точных моделей квантовых процессов, учитывающих влияние измерений на их кинетику и поведение.
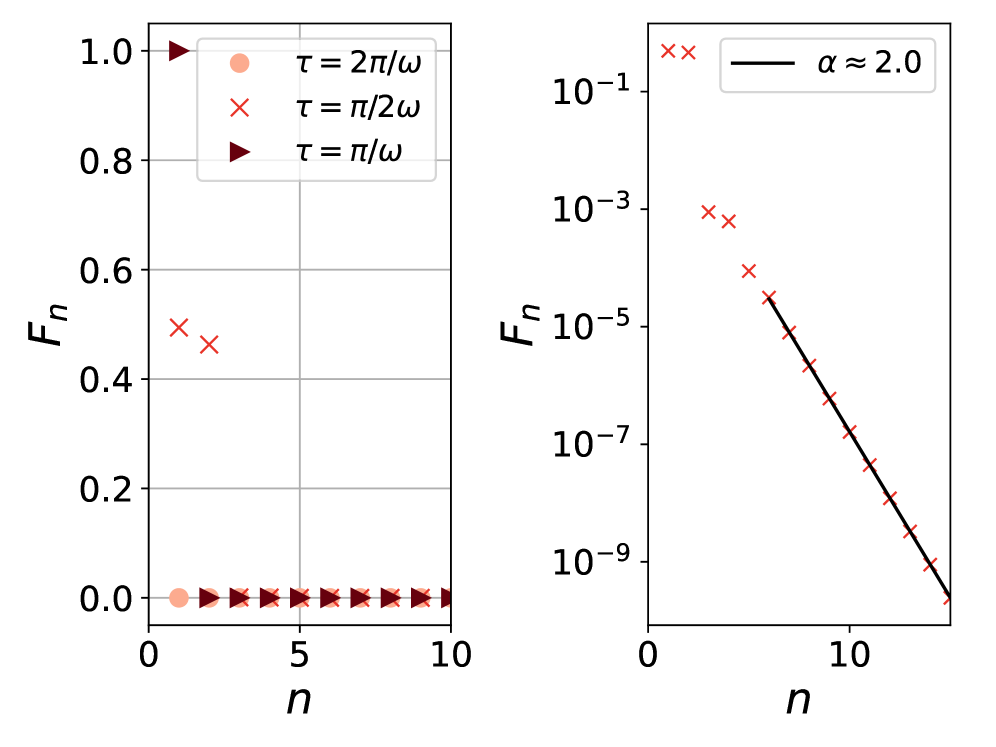
Исследование выявило существование резонансных интервалов для гармонического осциллятора, определяемых как \tau = \pi/ω и их кратные, где τ — интервал непрерывного измерения, а ω — частота осциллятора. В эти моменты времени вероятность детектирования частицы может быть как максимизирована, так и минимизирована, что демонстрирует возможность точного управления квантовой динамикой системы. Обнаружено, что при совпадении интервала измерения с резонансной частотой осциллятора, происходит существенное изменение вероятности обнаружения, позволяя, по сути, «настраивать» взаимодействие между системой и измерительным прибором. Такой контроль открывает перспективы для создания высокочувствительных квантовых сенсоров и манипулирования квантовыми состояниями с беспрецедентной точностью.
Полученные результаты имеют существенное значение для понимания скорости химических реакций, явления квантового туннелирования и динамики квантовых систем в зашумленных средах. Отклонение от экспоненциального затухания, вызванное непрерывными измерениями, напрямую влияет на вероятность протекания реакций и скорость туннелирования частиц через потенциальные барьеры. В частности, алгебраический распад, наблюдаемый в исследуемых системах, указывает на более медленное затухание вероятности нахождения частицы в определенной области, что может существенно замедлить реакции или увеличить вероятность туннелирования. Более того, учет влияния непрерывных измерений позволяет более реалистично моделировать динамику квантовых систем, подверженных шумам и взаимодействиям с окружающей средой, что особенно важно для разработки новых квантовых технологий и понимания поведения сложных квантовых систем в реальных условиях.
Данное исследование представляет собой важный шаг к включению эффектов измерения в реалистичные модели квантовых процессов. Традиционно, моделирование квантовых систем часто предполагает идеализированные условия, игнорируя влияние непрерывного наблюдения. Однако, представленные результаты демонстрируют, что постоянные измерения существенно изменяют динамику систем, приводя к отклонениям от привычной экспоненциальной убыли, и, вместо этого, проявляются более сложные закономерности, такие как степенное затухание и модифицированные скорости распада. Эти выводы открывают перспективы для разработки более точных и адекватных описаний квантовых явлений, учитывающих взаимодействие системы с измерительным прибором, что особенно важно при моделировании реакций, туннелирования и поведения квантовых систем в зашумленных средах. Созданный теоретический фундамент позволит в дальнейшем интегрировать эффекты измерения в более сложные модели, приближая их к реальным физическим условиям и расширяя возможности контроля над квантовой динамикой.
Исследование, представленное в данной работе, демонстрирует изящную взаимосвязь между актом измерения и динамикой квантовой частицы. Оно показывает, как само наблюдение влияет на статистику первого обнаружения, приводя к переходу от экспоненциального к алгебраическому спаду. Эта деликатная зависимость от энергетического спектра и ограничений системы напоминает о фундаментальной неразрывности наблюдателя и наблюдаемого. Как однажды заметил Карл Саган: «Мы — звёздная пыль, стремящаяся познать себя». Эта фраза отражает стремление к пониманию, лежащее в основе данной работы, где попытка измерить время первого обнаружения частицы приводит к раскрытию более глубоких закономерностей в квантовом мире. Элегантность этого открытия заключается не только в математической точности, но и в гармонии между теорией и экспериментом.
Куда же дальше?
Настоящая работа, исследуя зависимость времени первого обнаружения квантовой частицы от самого процесса измерения, лишь приоткрывает завесу над сложностью взаимодействия наблюдателя и наблюдаемого. Выявленный переход от экспоненциального к алгебраическому спаду, зависящий от энергетического спектра и условий удержания, скорее шепчет о глубинных принципах, нежели кричит о немедленных применениях. Очевидно, что дальнейшее углубление в тонкости стробоскопического измерения потребует не только более точных теоретических моделей, но и экспериментальной проверки предсказаний, что, как всегда, представляет собой изящную задачу.
Особенно интригующим представляется вопрос о границах применимости полученных результатов к системам с более сложными спектрами и многомерными потенциальными ямами. Уместно задуматься о роли декогеренции, которую в настоящей работе рассматривают как незначительный фактор, но которая в реальных экспериментах неизбежно вносит свой диссонанс. Не стоит забывать и о потенциальной связи с эффектом Зенона, где постоянное наблюдение парадоксальным образом замедляет эволюцию системы — здесь, кажется, все не так просто, как кажется на первый взгляд.
В конечном итоге, исследование первых моментов обнаружения — это не просто решение конкретной физической задачи, но и упражнение в понимании фундаментальных аспектов квантовой реальности. И как всякая элегантная теория, оно порождает больше вопросов, чем ответов, и, возможно, это и есть ее истинная ценность.
Оригинал статьи: https://arxiv.org/pdf/2601.12102.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Все рецепты культистского круга в Escape from Tarkov
- Решение головоломки с паролем Absolum в Yeldrim.
- Лучшие транспортные средства в Far Cry 6
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Как получить скины Alloyed Collective в Risk of Rain 2
- Репозиторий: Как исправить таймаут клиента
- 15 лучших законченных серий манхвы, которые стоит прочитать, в рейтинге
- The Planet Crafter: расположение ключей Стража
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- В стороне: QB и я В ролях: каждый актер, который появляется (фотографии)
2026-01-22 03:07