Квантовая запутанность в вакуумном распаде: от площади к объему

Автор: Денис Аветисян

Новое исследование показывает, как геометрическая запутанность изменяется при непертурбативном распаде вакуума в скалярном QED, известном как эффект Заутера-Швингера.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал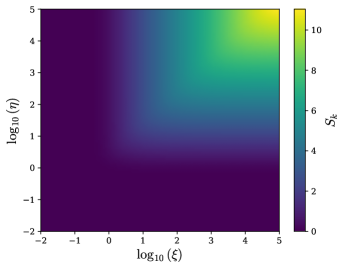

В эффекте Заутера-Швингера парная энтропия запутанности <span class="katex-eq" data-katex-display="false">S_{\mathbf{k}}</span> демонстрирует зависимость от импульса <span class="katex-eq" data-katex-display="false">\omega_{\mathbf{k}}^{+}=\mu</span>, что указывает на ключевую роль волнового вектора в формировании квантовой запутанности в вакууме. — В эффекте Заутера-Швингера парная энтропия запутанности $S_{\mathbf{k}}$ демонстрирует зависимость от импульса $\omega_{\mathbf{k}}^{+}=\mu$ , что указывает на ключевую роль волнового вектора в формировании квантовой запутанности в вакууме.

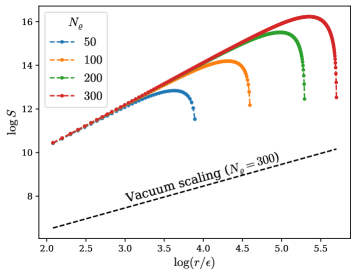
В работе исследуется переход от масштабирования закона площади к закону объема для энтропии запутанности при анализе эффекта Заутера-Швингера.

В квантовой теории поля, понимание корреляций между различными степенями свободы остается сложной задачей, особенно в непертурбативных режимах. Настоящая работа, посвященная исследованию ‘Entanglement scaling and dynamics in the Sauter-Schwinger effect’, представляет собой первое комплексное численное исследование динамики и геометрического масштабирования энтропии запутанности в сильном поле, возникающей в процессе эффекта Зоутера-Швингера. Показано, что при определенных параметрах импульса происходит переход от масштабирования, подчиняющегося закону площади, к масштабированию, подчиняющемуся закону объема, что свидетельствует о фундаментальном изменении структуры корреляций, индуцированном непертурбативным рождением пар. Каким образом полученные результаты могут пролить свет на природу запутанности в других непертурбативных процессах квантовой теории поля и внести вклад в развитие квантовой теории информации?

Запутанность: За гранью классических корреляций

Понимание квантовых корреляций, количественно оцениваемых с помощью энтропии запутанности, имеет решающее значение для исследования фундаментальной физики. В отличие от классических корреляций, квантовая запутанность демонстрирует нелокальные связи между частицами, которые невозможно объяснить в рамках классической физики. $S = -Tr(\rho \log \rho)$ — эта величина, характеризующая степень запутанности, позволяет исследовать свойства квантовых систем, выходящие за рамки традиционного понимания. Изучение энтропии запутанности предоставляет уникальную возможность для проверки предсказаний квантовой теории поля, а также для понимания структуры пространства-времени на микроскопическом уровне. Анализ поведения этой величины в различных квантовых системах позволяет выявлять новые физические явления и углублять наше понимание основ мироздания.

Традиционные методы оценки корреляции, разработанные для классических систем, оказываются недостаточными при изучении квантовых явлений. Они не способны адекватно описать сложные взаимосвязи между частицами, обусловленные принципами квантовой механики, такими как суперпозиция и запутанность. В то время как классические корреляции описывают статистическую зависимость между переменными, квантовые корреляции демонстрируют более глубокую и нелокальную связь, которая не может быть выражена через простые статистические зависимости. Это требует разработки новых аналитических инструментов и подходов, способных улавливать тонкости квантовых систем и описывать их уникальные свойства, такие как квантовая запутанность $\rho_{AB}$ и квантовая интерференция. Именно поэтому современные исследования все больше внимания уделяют разработке и применению квантовых мер корреляции, позволяющих более точно и полно описывать поведение квантовых систем.

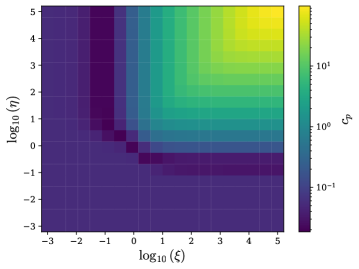
Энтропия запутанности, как мера квантовой корреляции, демонстрирует примечательную зависимость от размера исследуемой системы. В частности, её масштабирование описывается двумя основными закономерностями: законом площади и законом объема. Закон площади предполагает, что энтропия запутанности растет пропорционально площади границы системы, намекая на голографическую связь между гравитацией и квантовой механикой. В то время как закон объема указывает на рост энтропии пропорционально объему системы, что характерно для квантовых систем без четко определенной границы. Результаты проведенного исследования выявляют переход между этими двумя режимами масштабирования, что позволяет глубже понять структуру пространства-времени и особенности квантовой теории поля. Этот переход, наблюдаемый в конкретных условиях, предоставляет ценные сведения о взаимосвязи между геометрией пространства и квантовыми свойствами исследуемой системы, открывая новые горизонты в изучении фундаментальных основ физики. $S \sim A$ и $S \sim V$ — приблизительные выражения для закона площади и закона объема соответственно.

Анализ энтропии запутанности для различных размеров подсистем демонстрирует степенную зависимость, подтверждаемую результатами подгонки (при <span class="katex-eq" data-katex-display="false">\xi=10^2</span>, <span class="katex-eq" data-katex-display="false">\eta=10</span>, <span class="katex-eq" data-katex-display="false">\tilde{\mu}=1</span>, <span class="katex-eq" data-katex-display="false">N_z=100</span>, <span class="katex-eq" data-katex-display="false">N_\varrho=300</span> и <span class="katex-eq" data-katex-display="false">R/20 < r < R/4</span>), и показывает, что префактор этой зависимости остается стабильным. — Анализ энтропии запутанности для различных размеров подсистем демонстрирует степенную зависимость, подтверждаемую результатами подгонки (при $\xi=10^2$ , $\eta=10$ , $\tilde{\mu}=1$ , $N_z=100$ , $N_\varrho=300$ и $R/20 < r < R/4$ ), и показывает, что префактор этой зависимости остается стабильным.

Гауссовские состояния: Управляемый хаос

Многомодовые гауссовские состояния представляют собой мощный аналитически разрешимый подход к изучению многочастичных квантовых систем. В отличие от произвольных квантовых состояний, требующих экспоненциального количества параметров для описания, гауссовские состояния полностью характеризуются первыми и вторыми моментами операторов, что позволяет эффективно проводить вычисления. Это достигается за счет того, что эволюция гауссовского состояния под действием гамильтониана, содержащего только квадратичные члены, также остаётся гауссовским состоянием. Такая разрешимость делает их особенно полезными для анализа сложных систем, где точные решения недоступны, и позволяет сравнивать теоретические предсказания с результатами численного моделирования, например, в контексте квантовой информации и конденсированного состояния вещества. $\rho = \frac{1}{\pi^n} \in t \mathbb{R}^n e^{-x^T \Sigma^{-1} x} dx$

Характеризация многомодовых гауссовских состояний осуществляется посредством ковариационной матрицы и функции Вигнера. Ковариационная матрица σ полностью определяет корреляции между квадратурными переменными, описывающими состояние, а функция Вигнера $\rho(q,p)$ представляет собой квазивероятностное распределение по фазовому пространству. Вместе, эти инструменты позволяют полностью описать квантовые свойства состояния, включая его чистоту, энтропию и корреляции, без необходимости решения сложной многочастичной задачи. Таким образом, ковариационная матрица и функция Вигнера служат ключевыми параметрами для анализа и моделирования гауссовских состояний в квантовых системах.

Использование многомодовых гауссовых состояний позволяет эффективно вычислять энтропию запутанности, что обеспечивает связь между теоретическими предсказаниями и численными симуляциями. Наши расчеты демонстрируют переменную степень закона и предварительный коэффициент в выражении для энтропии, указывающие на отклонения от стандартного масштабирования по площади $S \sim L^{d-1}$ , где $L$ — размер системы, а $d$ — ее размерность. Наблюдаемые отклонения свидетельствуют о нетривиальной структуре запутанности в исследуемых системах и требуют более детального анализа для определения природы этих эффектов.

Анализ энтропии запутанности в эффекте Соутера-Швингера показывает, что она масштабируется по степенному закону <span class="katex-eq" data-katex-display="false">S \sim r^{p}</span> с показателем <span class="katex-eq" data-katex-display="false">p \approx 0.8</span> и префактором <span class="katex-eq" data-katex-display="false">c_{p}</span>, что подтверждено высокой точностью аппроксимации (R² ≈ 0.999) в диапазоне <span class="katex-eq" data-katex-display="false">R/20 < r < R/4</span>. — Анализ энтропии запутанности в эффекте Соутера-Швингера показывает, что она масштабируется по степенному закону $S \sim r^{p}$ с показателем $p \approx 0.8$ и префактором $c_{p}$ , что подтверждено высокой точностью аппроксимации (R² ≈ 0.999) в диапазоне $R/20 < r < R/4$ .

Эффект Заутера-Швингера: Рождение из ничто

Эффект Заутера-Швингера предсказывает создание пар частица-античастица из вакуума под воздействием сильного электрического поля. В квантовой электродинамике вакуум рассматривается не как пустота, а как состояние с минимальной энергией, постоянно подвергающееся квантовым флуктуациям. При достаточно сильном электрическом поле $E$ , энергия, передаваемая этим флуктуациям, может стать достаточной для рождения виртуальной пары частица-античастица, которая затем становится реальной. Интенсивность рождения пар пропорциональна $exp(- \pi E_c / E)$ , где $E_c$ — критическое поле Швингера, определяющее порог для значительного рождения пар. Этот процесс является непертурбативным и не может быть описан стандартной теорией возмущений.

Для моделирования эффекта Заутера-Швингера используется комплексное скалярное поле, подвергающееся воздействию временного импульса Заутера. Математически, это описывается уравнением Клейна-Гордона с внешним электромагнитным полем, представляющим импульс. Импульс Заутера характеризуется медленным изменением напряженности электрического поля во времени, что позволяет использовать приближение слабого поля для упрощения анализа. Использование комплексного поля позволяет учесть как положительные, так и отрицательные энергетические состояния, необходимые для описания рождения пар частица-античастица из вакуума. Конкретно, поле описывается функцией $\Psi(x,t)$ , где $x$ — пространственная координата, а $t$ — время, и взаимодействует с векторным потенциалом $A(t)$ , определяющим напряженность электрического поля.

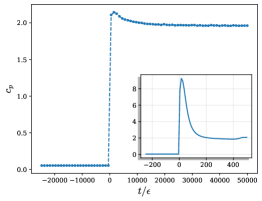
Адиабатическое приближение значительно упрощает расчеты при анализе эффекта Соутера-Швингера, позволяя исследовать скорости распада вакуума и процессы рождения частиц. В частности, при определенных значениях напряженности электрического поля наблюдается переход от масштабирования, подчиняющегося закону площади ( $Area-Law$ ), к масштабированию, подчиняющемуся закону объема ( $Volume-Law$ ). Этот переход четко проявляется в изменении коэффициента масштабирования, что позволяет количественно оценить взаимосвязь между корреляциями в подсистемах и физическими процессами, происходящими в квантовом поле. Полученные результаты подчеркивают важность данного подхода для понимания структуры квантовой запутанности и ее влияния на динамику системы.

В сильном поле наблюдается появление нелокальных корреляционных пиков, свидетельствующих о создании пар частиц в результате эффекта Заутера-Швингера, в то время как в слабом поле такая корреляция отсутствует (при <span class="katex-eq" data-katex-display="false">\tilde{\mu}=1</span> и <span class="katex-eq" data-katex-display="false">N_{\varrho}=300</span>). — В сильном поле наблюдается появление нелокальных корреляционных пиков, свидетельствующих о создании пар частиц в результате эффекта Заутера-Швингера, в то время как в слабом поле такая корреляция отсутствует (при $\tilde{\mu}=1$ и $N_{\varrho}=300$ ).

Математический аппарат: Описание квантовых полей

Уравнение Клейна — Гордона является фундаментальным уравнением в квантовой теории поля, описывающим динамику комплексного скалярного поля. Оно представляет собой релятивистское обобщение уравнения Шрёдингера и позволяет описывать поведение частиц, обладающих спином, равным нулю. Решение этого уравнения дает информацию о том, как поле эволюционирует во времени и пространстве, определяя возможные состояния и энергии частиц. $(\partial^\mu \partial_\mu + m^2) \phi(x) = 0$ — именно эта форма записи демонстрирует связь между энергией, импульсом и массой частицы, что критически важно для понимания релятивистской квантовой механики. Именно благодаря этому уравнению становится возможным построение квантовых теорий для различных элементарных частиц и сил.

При анализе квантовых полей, обладающих цилиндрической симметрией, переход к цилиндрической системе координат значительно упрощает математический аппарат. Вместо использования привычных декартовых координат (x, y, z), описывающих положение точки в пространстве, вводятся цилиндрические координаты (ρ, φ, z), где ρ — радиальное расстояние от оси симметрии, φ — азимутальный угол, а z — высота вдоль оси. Такой подход позволяет разделить переменные в волновом уравнении, например, в уравнении Клейна-Гордона $(\frac{\partial^2}{\partial t^2} - \nabla^2 + m^2) \phi(x) = 0$ , что существенно облегчает поиск решений и анализ поведения поля. Использование цилиндрических координат позволяет представить поле как сумму независимых функций от каждой координаты, что приводит к упрощению вычислений и более наглядному пониманию физических свойств рассматриваемого квантового поля.

Решения уравнений квантовых полей, известные как модельные функции, представляют собой фундаментальный инструмент для описания всех возможных состояний поля. Эти функции не просто математические конструкции, а физические представления различных способов, которыми поле может колебаться и проявлять энергию. Каждая модельная функция соответствует определенному квантовому состоянию, характеризующемуся конкретным импульсом и спином частицы. $\phi(x)$ — типичный пример модельной функции, описывающей эволюцию поля в пространстве и времени. Изучение этих функций позволяет понять, как формируются частицы, как они взаимодействуют друг с другом и как проявляются квантовые эффекты в различных физических процессах. Таким образом, модельные функции служат мостом между абстрактной математикой квантовой теории поля и наблюдаемыми явлениями в микромире.

Переход от стандартной решетчатой регуляризации в цилиндрических координатах к размерно-уменьшенному представлению позволяет получить эффективную решетчатую теорию в 1+1 измерениях.

Квантовые корреляции: Пространственное разделение

Пространственное разделение представляет собой основополагающий метод в квантовой механике, позволяющий разделить сложную квантовую систему на более простые, взаимосвязанные подсистемы. Этот подход позволяет изучать корреляции и запутанность между различными частями системы, что особенно важно при анализе многочастичных состояний и квантовых полей. Разделение пространства на отдельные регионы позволяет исследовать, как информация распределяется между ними и как эти подсистемы взаимодействуют друг с другом. По сути, это фундаментальный инструмент для понимания структуры и свойств квантовых систем, особенно в контексте таких явлений, как квантовая запутанность и переход от локальных к нелокальным корреляциям. Использование пространственного разделения позволяет упростить анализ сложных систем, выделив ключевые степени свободы и их взаимосвязи.

Пространственное разделение, в сочетании с принципами гауссовских состояний и рамками энтропии запутанности, позволяет количественно оценить корреляции между подсистемами квантовой системы. Используя гауссовские состояния, можно эффективно описывать широкий класс квантовых систем, а энтропия запутанности выступает мерой неклассической корреляции между подсистемами, определяя степень их взаимосвязанности. Этот подход позволяет не только выявить наличие корреляций, но и точно измерить их силу, предоставляя ценные инструменты для анализа сложных квантовых явлений и разработки новых квантовых технологий. Анализ масштабирования энтропии запутанности, в частности, дает возможность понять, как информация распределяется между подсистемами и как изменяется характер этих корреляций при различных условиях.

Разделение квантового поля на вещественную и мнимую части позволяет провести его детальный анализ с использованием квадратурных операторов. Исследование показало, что переход от масштабирования, подчиняющегося закону площади ( $Area-Law$ ), к масштабированию, подчиняющемуся закону объема ( $Volume-Law$ ), тесно связан с режимом интенсивного рождения пар частиц. Этот переход четко проявляется в изменении коэффициента масштабирования, что позволяет количественно оценить взаимосвязь между корреляциями в подсистемах и физическими процессами, происходящими в квантовом поле. Полученные результаты подчеркивают важность данного подхода для понимания структуры квантовой запутанности и ее влияния на динамику системы.

Анализ масштабирования энтропии запутанности для вакуумного состояния и конечного состояния <span class="katex-eq" data-katex-display="false">t/\tau=10^{20}</span> при <span class="katex-eq" data-katex-display="false">\xi=10^{2}</span>, <span class="katex-eq" data-katex-display="false">\eta=10</span>, <span class="katex-eq" data-katex-display="false">\tilde{\mu}=1</span> и <span class="katex-eq" data-katex-display="false">N_{z}=100</span> показывает, что энтропия масштабируется с изменением <span class="katex-eq" data-katex-display="false">N_{\varrho}</span>. — Анализ масштабирования энтропии запутанности для вакуумного состояния и конечного состояния $t/\tau=10^{20}$ при $\xi=10^{2}$ , $\eta=10$ , $\tilde{\mu}=1$ и $N_{z}=100$ показывает, что энтропия масштабируется с изменением $N_{\varrho}$ .

Статья рассматривает запутанность как геометрическое свойство, возникающее при вакуумном распаде в скалярном QED, что не может не вызвать ироничную усмешку. По сути, описывается переход от законов площади к законам объема в отношении энтропии запутанности. Кажется, даже в квантовой физике, где всё подчиняется строгим законам, рано или поздно наступает момент, когда теория уступает место практике. Как метко заметил Фридрих Ницше: «Без музыки жизнь была бы ошибкой». Здесь можно провести аналогию: без понимания, что даже самые элегантные математические модели в конечном итоге сталкиваются с реальностью, все эти расчеты энтропии и ковариационных матриц были бы просто красивой, но бесполезной ошибкой. Продакшен, в данном случае — сам процесс вакуумного распада — всегда найдет способ сломать эту элегантную теорию, подтверждая, что даже в квантовом мире «всё новое — это старое, только с другим именем и теми же багами».

Что дальше?

Изучение масштабирования запутанности в эффекте Заутера-Швингера, несомненно, добавляет ещё один уровень сложности в и без того запутанный мир непертурбативных процессов в квантовой теории поля. Однако, следует помнить: каждая элегантная формула, описывающая рост запутанности, рано или поздно встретит суровую реальность численных методов. Все эти «законы», переходящие от площадных к объемным, лишь демонстрируют, что ещё не нашли способ заставить систему сломаться по-новому.

Наиболее очевидная проблема — это, конечно, расширение рассмотрения за пределы скалярного электродинамики. Фермионные поля, взаимодействия более высокой спинности — все это лишь новые способы усложнить ковариационную матрицу. Если баг воспроизводится в разных моделях — это не признак стабильности, а свидетельство того, что мы просто не умеем искать ошибки.

В конечном итоге, стоит признать, что документация по вычислению энтропии запутанности — это форма коллективного самообмана. Каждая «самовосстанавливающаяся» система просто ещё не столкнулась с достаточно изощренным способом выхода из строя. А значит, работы в этом направлении предстоит ещё очень много. И, скорее всего, всё закончится тем, что кто-нибудь напишет очередной фреймворк, который будет требовать переписывания всего кода.

Оригинал статьи: https://arxiv.org/pdf/2601.14390.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-22 13:11