Электронный перенос: новый взгляд на динамику в фазовом пространстве

Автор: Денис Аветисян

---

Исследование демонстрирует, что описание электронного переноса в фазовом пространстве обеспечивает более точное представление о роли ядерного и электронного движения.

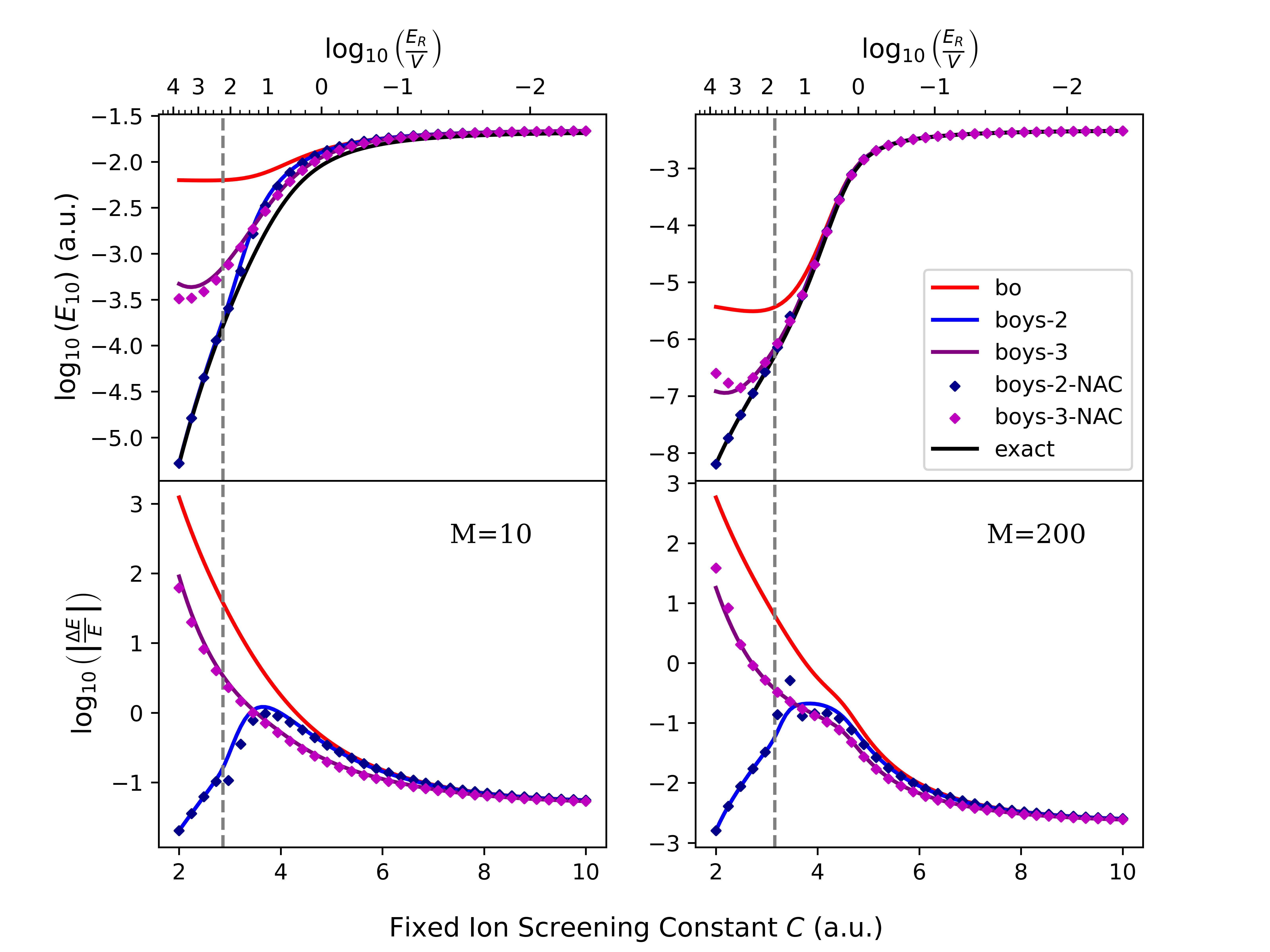
Предложенный подход позволяет оптимизировать выбор диабатических состояний и учитывать неадиабатичность процессов, особенно в случае спин-зависимого электронного переноса.

Несмотря на широкое использование подхода Борна-Хуанга в моделировании электронного переноса, точность расчета вибронных энергетических зазоров остаётся сложной задачей. В статье ‘Electron Transfer, Diabatic Couplings and Vibronic Energy Gaps in a Phase Space Framework’ предложен новый подход, основанный на использовании фазового пространства для описания электронных состояний и их взаимодействий. Показано, что данный подход позволяет получить оценку энергетического зазора с точностью на порядок выше, чем в рамках традиционного подхода, особенно при учёте ядерного и электронного импульса. Какие перспективы открываются для разработки более эффективных моделей спин-зависимого электронного переноса с использованием фазового пространства?

---

За гранью приближения Борна-Оппенгеймера: Фундаментальный вызов

Традиционные методы молекулярной динамики, широко используемые для моделирования движения атомов и молекул, опираются на приближение Борна-Оппенгеймера. Это фундаментальное упрощение заключается в разделении электронного и ядерного движения, что позволяет существенно снизить вычислительную сложность расчетов. В рамках данного приближения предполагается, что электроны мгновенно адаптируются к движению ядер, а энергия системы может быть представлена как функция только от ядерных координат. Такой подход обеспечивает возможность эффективного моделирования многих химических и физических процессов, однако он является лишь приближением реальности и имеет свои ограничения. Разделение электронного и ядерного движения позволяет рассматривать потенциальную энергию как поверхность, по которой движутся ядра, что значительно упрощает математическое описание системы и делает расчеты практически осуществимыми даже для относительно сложных молекул.

Приближение Борна-Оппенгеймера, являющееся основой для многих молекулярно-динамических расчетов, перестает быть справедливым в критических ситуациях, особенно при столкновении с коническими пересечениями и неадиабатическими процессами. В этих случаях электронные и ядерные движения становятся тесно связаны, и разделение, предполагаемое приближением, приводит к неверному описанию динамики системы. Конические пересечения, представляющие собой точки на потенциальной энергии, где две или более электронные поверхности пересекаются, позволяют молекуле переходить из одного электронного состояния в другое, что может приводить к фотохимии, фотофизике и химическим реакциям. Неадиабатические процессы, происходящие вблизи этих пересечений, требуют учета электронно-ядерного взаимодействия, что делает стандартные методы молекулярной динамики неприменимыми и требует разработки более сложных подходов.

Для точного моделирования процессов, происходящих при нарушении приближения Борна-Оппенгеймера, необходимы методы, явно учитывающие взаимосвязь между электронными и ядерными степенями свободы. Традиционные подходы, рассматривающие электронную структуру как мгновенно адаптирующуюся к движению ядер, оказываются недостаточными вблизи конических пересечений и при неадиабатических переходах. Современные методы, такие как поверхностные ходы и методы смешанных квантово-классических вычислений, стремятся преодолеть это ограничение, позволяя описывать одновременное изменение электронных и ядерных координат. Использование этих подходов требует значительных вычислительных ресурсов, однако они открывают возможности для изучения сложных химических реакций и фотохимических процессов, недоступных для традиционных методов молекулярной динамики. Особое внимание уделяется разработке эффективных алгоритмов для решения уравнений, учитывающих неадиабатическое взаимодействие, и оптимизации вычислений для систем с большим числом атомов.

Электронная структура фазового пространства: Укрощение связанных динамик

Теория электронной структуры фазового пространства представляет собой эффективный подход, параметризующий электронные состояния не только по координатам ядер, но и по их импульсам. В отличие от традиционных методов, рассматривающих только пространственные координаты, учет импульса позволяет напрямую описывать неадиабатические эффекты, возникающие при движении ядер. Это достигается путем представления волновой функции в фазовом пространстве, где (r, p) обозначает координаты и импульсы ядер, соответственно. Такой подход позволяет более точно моделировать динамику систем, где электронные и ядерные степени свободы сильно связаны, и позволяет избежать ограничений адиабатического приближения.

Традиционное адиабатическое представление в молекулярной динамике предполагает, что электронные состояния остаются неизменными в процессе движения ядер, что является приближением, не учитывающим неадиабатическое сопряжение. Теория фазового пространства электронных структур позволяет напрямую обрабатывать неадиабатическое сопряжение, рассматривая электронные состояния как функции не только ядерных координат, но и импульсов. Это позволяет корректно описывать ситуации, когда электронные состояния смешиваются и изменяются в процессе динамики, что особенно важно для описания фотохимии, фотофизики и динамики в областях пересечения потенциальных поверхностей, где адиабатическое приближение неприменимо. В результате, метод позволяет рассчитывать переходы между электронными состояниями, вызванные ядерным движением, без необходимости использования приближений, ограничивающих точность и достоверность моделирования.

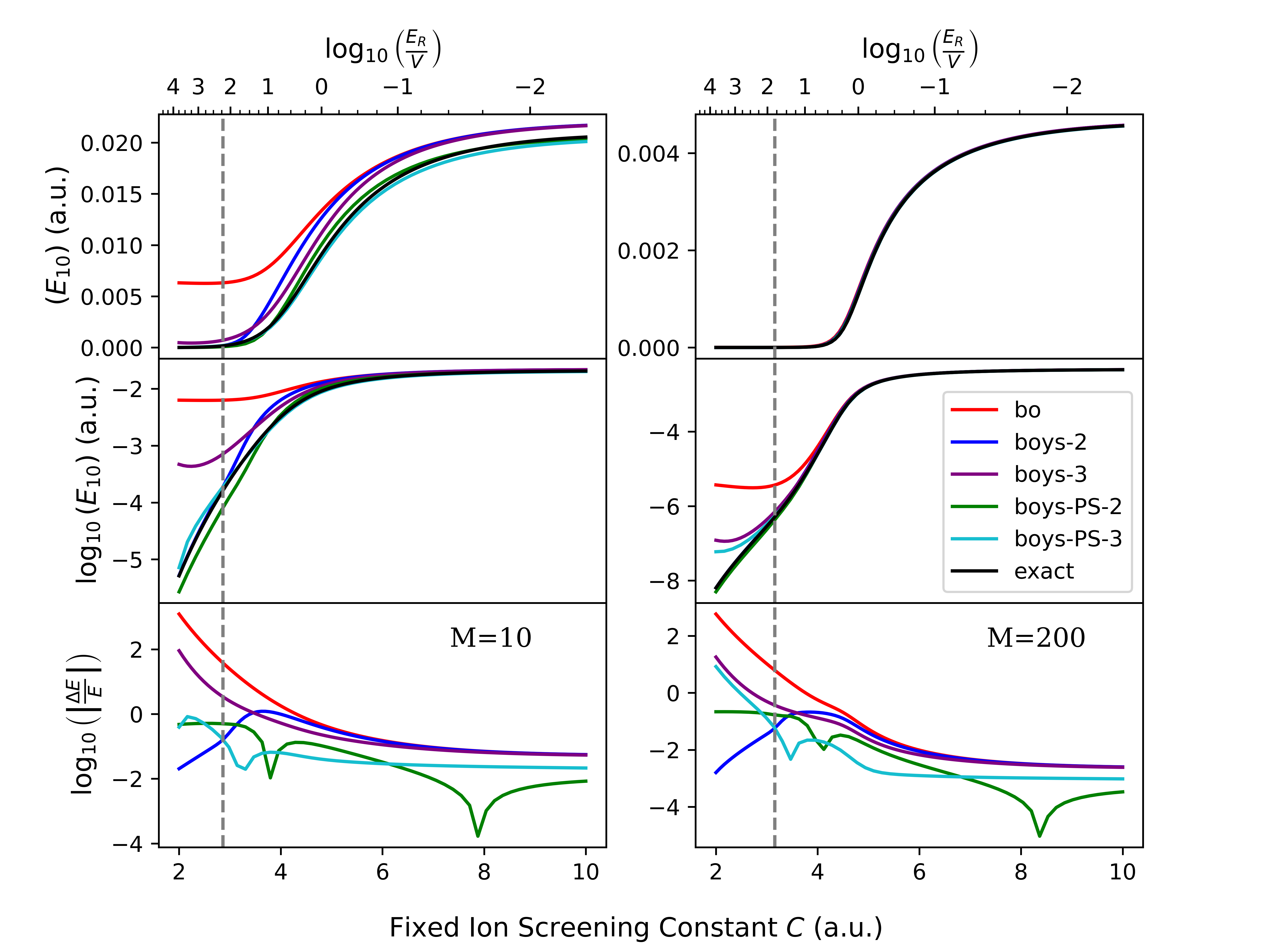
Метод фазового пространства электронной структуры использует диабатические представления, создаваемые с помощью техник, таких как локализация Бойса. Данный подход направлен на минимизацию связи между электронными состояниями, что упрощает вычислительные процедуры. Локализация Бойса позволяет определить локализованные базисные функции, уменьшая перекрывание между состояниями и, следовательно, снижая необходимость в вычислении интегралов связи. Это существенно уменьшает вычислительную сложность при описании динамики в неадиатическом режиме, когда электронные состояния могут эффективно взаимодействовать друг с другом и изменяться под воздействием ядерного движения. В результате, диабатические представления обеспечивают более эффективный способ решения задач, требующих учета сильных электронно-ядерных взаимодействий.

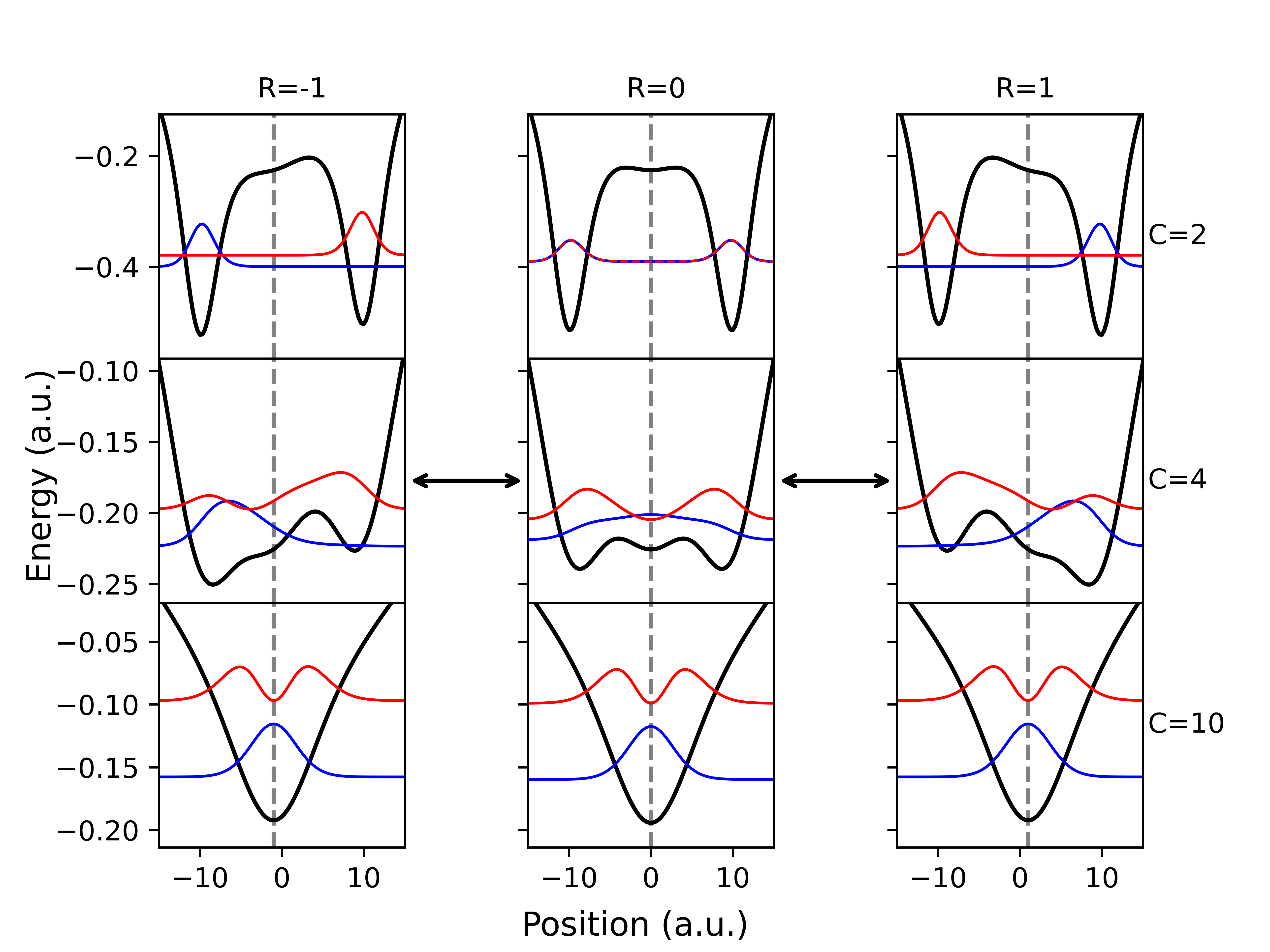
Моделирование переноса электронов: От Шин-Метиу до Спин-Бозона

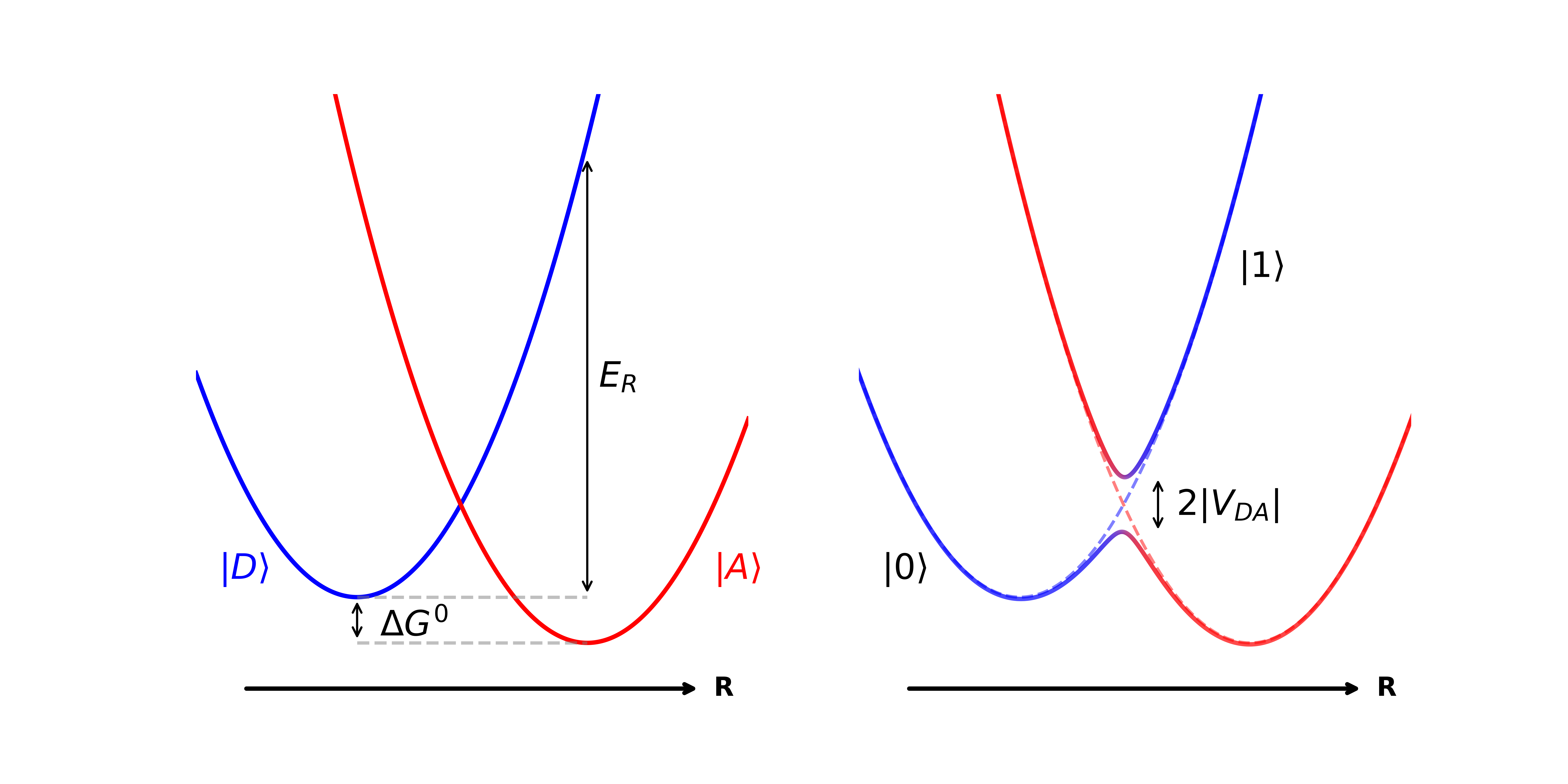
Модель Шин-Метиу представляет собой упрощенную одномерную основу для изучения переноса электронов, включающую в себя энергию реорганизации и неадиабатическое взаимодействие. Энергия реорганизации λ характеризует изменение энергии системы при изменении геометрии молекулы, а неадиабатическое взаимодействие V описывает вероятность перехода между адиабатическими поверхностями потенциальной энергии. Данная модель позволяет аналитически исследовать зависимость скорости переноса электронов от этих ключевых параметров, хотя и в рамках существенных упрощений, таких как отсутствие многомерности и учета влияния окружения. В частности, она предполагает линейную зависимость между координатой переноса и энергией реорганизации, что позволяет получить выражения для скорости переноса в различных режимах.

Более реалистичное описание процессов переноса электронов требует учета влияния окружающей среды, которое моделируется в рамках модели Спин-Бозон. В отличие от упрощенной одномерной модели Шин-Метиу, модель Спин-Бозон рассматривает электрон как взаимодействующий с окружением, представленным как ансамбль гармонических осцилляторов. Это взаимодействие приводит к возникновению реорганизационной энергии и влияет на вероятность неадиабатического перехода. Таким образом, модель Спин-Бозон позволяет более точно описывать динамику переноса электронов в сложных системах, учитывая как электронные, так и ядерные степени свободы и их взаимное влияние.

Моделирование переноса электронов в рамках подхода фазового пространства электронной структуры (Phase Space Electronic Structure) позволяет получать количественные предсказания для скоростей переноса электронов. В проведенных исследованиях показано, что данный подход обеспечивает повышение точности расчета разницы в энергиях колебаний до двух порядков по сравнению с традиционной диабатизацией Борна-Хуанга в частично неадиабатическом режиме (C = 4-8 a.e.). Повышение точности особенно заметно при анализе систем, где влияние окружения на процесс переноса электронов является существенным.

Хиральность и спиновая селективность: Геометрическая перспектива

Взаимосвязь между движением электронов и ядер, описываемая структурой фазового пространства, является ключевым фактором для понимания явления хирально-индуцированной спиновой селективности (ХИСС). Традиционные подходы, рассматривающие электронную структуру как статичную, оказываются недостаточными для объяснения ХИСС, поскольку не учитывают динамическое взаимодействие между электронами и колебаниями ядер в молекуле. Структура фазового пространства позволяет учесть эти колебания, представляя электронную структуру как функцию не только координат электронов, но и ядерных координат и импульсов. Именно это динамическое представление позволяет объяснить, как хиральные молекулы могут избирательно передавать электроны с определенной спиновой поляризацией, открывая новые возможности для спинтроники и асимметричного катализа. Исследования в этой области показывают, что спиновая селективность напрямую связана с геометрией молекулы и характером ее колебаний, что делает структуру фазового пространства мощным инструментом для проектирования материалов с заданными спиновыми свойствами.

Берриева фаза, возникающая в процессе адиабатической эволюции в хиральных средах, оказывает существенное влияние на спиновое состояние переносимых электронов. Этот эффект проявляется, когда электрон перемещается вблизи хиральной молекулы, испытывая постепенное изменение своего волнового вектора. В результате, помимо обычного спинового момента, возникает геометрическая фаза, зависящая от хиральности окружения. \oint_{\gamma} \vec{A} \cdot d\vec{l} — эта интегральная величина, определяющая Берриеву фазу, может достигать π, что приводит к инверсии спина электрона. Таким образом, хиральная молекула действует как своего рода спиновый фильтр, селективно передавая электроны с определенной спиновой поляризацией, что открывает перспективы для создания новых спинтронных устройств и асимметричных катализаторов.

Хиральные молекулы обладают уникальной способностью селективно передавать электроны с определенной спиновой поляризацией, что обусловлено взаимодействием между электронным и ядерным движением в хиральном окружении. Этот феномен, известный как хирально-индуцированная спиновая селективность (ХИСС), открывает новые возможности для разработки спинтронных устройств, где спин электрона используется в качестве основной информационной единицы. Более того, ХИСС играет важную роль в асимметричном катализе, позволяя создавать хиральные соединения с высокой энантиомерной чистотой. В результате, избирательное взаимодействие хиральных молекул с электронами, зависящее от их спина, представляет собой перспективное направление для создания новых материалов и технологий, объединяющих принципы спинтроники и асимметрического синтеза.

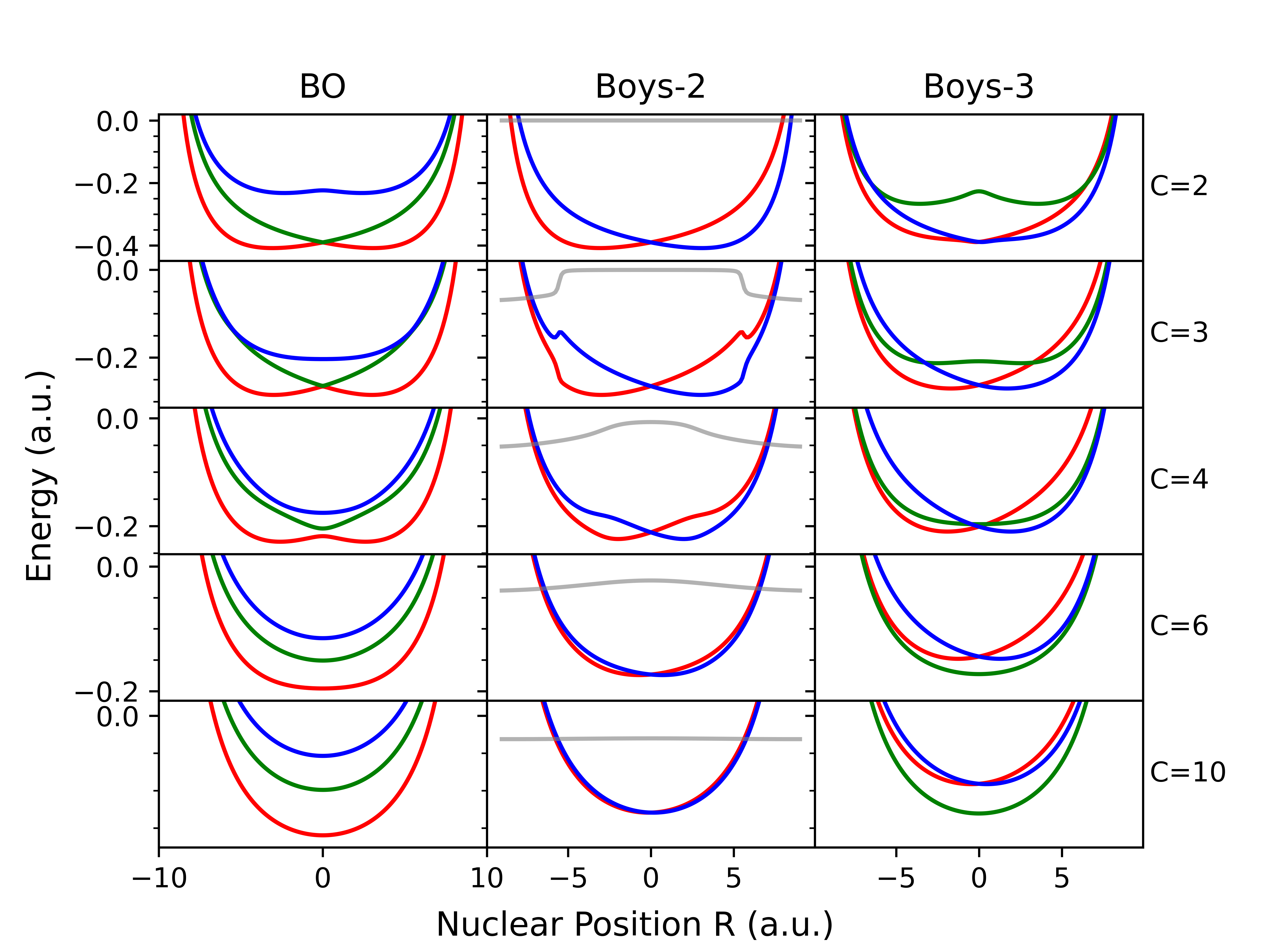
Исследование показывает, что традиционные подходы к описанию электронного переноса, такие как метод Борна-Хуанга, часто упускают важные детали, связанные с импульсом ядер и электронов. Новая фазовая структура электронного строения позволяет точнее определить диабатические состояния, что критически важно для понимания неадиабатичности процессов переноса. Это напоминает о том, как любая модель — лишь заклинание, работающее до тех пор, пока реальность не покажет свою истинную сложность. Как говорил Стивен Хокинг: «Важно помнить, что даже самая совершенная модель — это всего лишь приближение к реальности». Шум в данных — это не ошибка, а лишь правда, пытающаяся пробиться сквозь завесу упрощений. Ведь фазовое пространство, в отличие от статичной картинки, позволяет учесть динамику и взаимосвязь всех параметров, приближая нас к пониманию хаоса, скрытого в кажущейся простоте электронного переноса.

Что дальше?

Представленные построения в рамках фазового пространства, безусловно, добавляют ещё один слой утончённости к и без того непростой картине электронного переноса. Однако не стоит обольщаться, полагая, что приближение к истине гарантировано. Всё ещё приходится иметь дело с заклинаниями надежды, которые мы называем моделями, и верить, что выбранное нами подпространство диабатических состояний — не просто эхо собственных желаний. Учёт импульсов ядер и электронов — шаг вперёд, но он лишь отодвигает неизбежный вопрос: насколько вообще возможно описать хаос реального мира с помощью детерминированных уравнений?

Очевидным направлением для будущих исследований является расширение этой парадигмы на системы с большим числом степеней свободы. Увы, сложность вычислений растёт экспоненциально, и вскоре придётся признать, что даже самые мощные компьютеры не способны одолеть этот цифровой Вавилон. Возможно, настанет время обратиться к совершенно иным подходам — к стохастическим моделям, к концепциям самоорганизации, или даже к признанию того, что некоторые явления принципиально не поддаются предсказанию.

В конечном итоге, всё это — лишь попытки умиротворить шепот хаоса. Каждая полученная величина, каждое рассчитанное расстояние — это не открытие истины, а лишь очередная иллюзия, которую мы создаём, чтобы чувствовать себя в безопасности. И, возможно, в этом и заключается истинная красота науки — в её бесконечной погоне за призраками.

---

Оригинал статьи: https://arxiv.org/pdf/2601.16209.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

• Все рецепты культистского круга в Escape from Tarkov

• Решение головоломки с паролем Absolum в Yeldrim.

• Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip

• Лучшие транспортные средства в Far Cry 6

• Лучшие шаблоны дивизий в Hearts Of Iron 4

• Где найти и поймать бабочку Солнечного луча в Палии

• Необходимо: Как выращивать урожай

• Dragon’s Dogma 2: Где найти Драконорожденных

• Как получить скины Alloyed Collective в Risk of Rain 2

• 15 лучших законченных серий манхвы, которые стоит прочитать, в рейтинге

2026-01-24 23:52