Эхо черных дыр: нелинейные эффекты в отголосках массивных полей

Автор: Денис Аветисян

Новое исследование показывает, что нелинейные искажения оказывают незначительное влияние на затухающие колебания вокруг черных дыр, возникающие при возмущении массивными скалярными полями.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал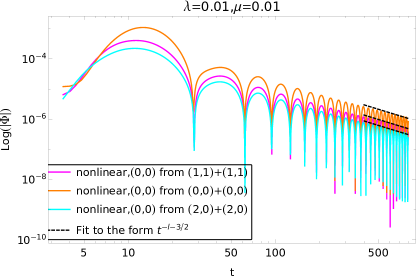

Массивные скалярные возмущения, эволюционирующие в нелинейных симуляциях, демонстрируют, что мода <span class="katex-eq" data-katex-display="false">(0,0)</span> формируется посредством квадратичного самодействия мод <span class="katex-eq" data-katex-display="false">(1,1)</span>, <span class="katex-eq" data-katex-display="false">(0,0)</span> и <span class="katex-eq" data-katex-display="false">(2,0)</span>, причем аналитические предсказания для промежуточных временных отрезков находятся в превосходном соответствии с результатами нелинейного численного моделирования, что подтверждает предложенный механизм формирования возмущений. — Массивные скалярные возмущения, эволюционирующие в нелинейных симуляциях, демонстрируют, что мода $(0,0)$ формируется посредством квадратичного самодействия мод $(1,1)$ , $(0,0)$ и $(2,0)$ , причем аналитические предсказания для промежуточных временных отрезков находятся в превосходном соответствии с результатами нелинейного численного моделирования, что подтверждает предложенный механизм формирования возмущений.

Работа посвящена анализу нелинейных эффектов в промежуточных временах для возмущений массивных скалярных полей вблизи черных дыр, с акцентом на квазинормальные моды второго порядка.

Нелинейные эффекты, играющие ключевую роль в финальной стадии затухания чёрных дыр, остаются недостаточно изученными для массивных скалярных полей. В работе ‘Nonlinear tails of massive scalar fields around a black hole’ систематически исследуются нелинейные хвосты возмущений, от упрощенной модели до самодействующего скалярного поля. Полученные результаты показывают, что в промежуточные моменты времени нелинейные хвосты массивных скалярных полей затухают с той же скоростью, что и линейные, вне зависимости от параметров источника. Могут ли квадратичные квазинормальные моды послужить индикатором нелинейной динамики массивных полей вокруг чёрных дыр?

Загадка Затухания: Изучение Колебаний Черных Дыр

После слияния чёрных дыр возникает финальная стадия — затухание, или ‘ringdown’, представляющая собой уникальную возможность для проверки теорий гравитации. Этот поздний сигнал, характеризующийся экспоненциально затухающими колебаниями, несёт в себе информацию о самой природе гравитационного поля и свойствах образовавшейся чёрной дыры. Изучение частоты и скорости затухания этих колебаний позволяет учёным измерять массу и спин чёрной дыры, а также тестировать предсказания общей теории относительности в экстремальных условиях. В частности, отклонения от теоретических моделей могут указывать на существование новой физики за пределами существующего понимания гравитации, что делает анализ ‘ringdown’ одним из ключевых направлений современной гравитационно-волновой астрономии. $e^{-i\omega t}$ — эта простая формула описывает основу затухающих колебаний, содержащих ключевую информацию.

Традиционно, финальная стадия слияния черных дыр, известная как «ringdown», успешно описывается теорией линейных возмущений. Данный подход предсказывает экспоненциально затухающие колебания, формирующие характерный «хвост Прайса» — медленно угасающую последовательность частот, возникающую из-за гравитационных волн, распространяющихся в искривленном пространстве-времени. $e^{-t/\tau}$ — именно эта экспоненциальная функция определяет скорость затухания сигнала, где τ — характерное время. Теория линейных возмущений позволяет достаточно точно моделировать этот процесс при условии, что возмущения гравитационного поля относительно слабы, что долгое время считалось адекватным приближением для описания слияний черных дыр.

Традиционная теория линейных возмущений, успешно описывающая финальную стадию слияния чёрных дыр — затухание колебаний, базируется на предположении о слабости возмущений гравитационного поля. Однако, в реальности, слияние черных дыр — это крайне нелинейный процесс, где гравитационные волны взаимодействуют друг с другом и с искривлением пространства-времени. Поэтому, несмотря на впечатляющую точность предсказаний теории линейных возмущений, существует вероятность, что она упускает из виду тонкие, но значимые нелинейные эффекты, проявляющиеся в затухании колебаний. Изучение этих нелинейных эффектов может предоставить более полное понимание гравитации в экстремальных условиях и потребовать разработки новых теоретических моделей, выходящих за рамки стандартной теории возмущений.

Временная эволюция скалярных возмущений как в безмассовом, так и в массивном случаях, как для линейных, так и нелинейных приближений, демонстрирует отличное соответствие между аналитическими предсказаниями и численными данными, особенно для массивного случая, где аналитические решения точно описывают эволюцию в обоих режимах.

Массивные Поля и Модифицированные «Хвосты»

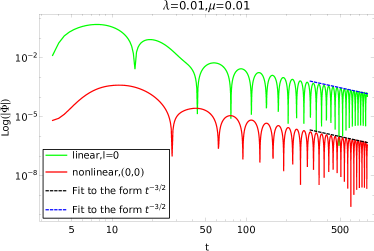
Присутствие массивного скалярного поля вокруг чёрной дыры Шварцшильда вносит масс-зависимые модификации в сигнал затухания (ringdown). Эти модификации проявляются в изменении частот и скоростей затухания квазинормальных мод, которые характеризуют гравитационные волны, излучаемые после слияния чёрных дыр или других возмущений. Величина этих изменений напрямую зависит от массы скалярного поля; чем больше масса поля, тем сильнее отклонения от предсказаний общей теории относительности для чёрной дыры Шварцшильда. Анализ этих отклонений в наблюдаемых сигналах гравитационных волн может предоставить информацию о массе и других свойствах скалярного поля, что позволяет использовать гравитационно-волновые наблюдения для проверки различных теорий гравитации и поиска новых частиц.

Присутствие массивного скалярного поля вокруг чёрной дыры Шварцшильда влияет на характер затухания сигнала $Price Tail$ . Данный «хвост» сигнала, возникающий после слияния чёрных дыр, обычно экспоненциально затухает. Однако, взаимодействие с массивным скалярным полем модифицирует эту скорость затухания, приводя к отклонениям от стандартной экспоненциальной зависимости. Анализ этих отклонений позволяет оценить массу скалярного поля, поскольку скорость затухания $Price Tail$ обратно пропорциональна массе поля. Таким образом, изучение модифицированного «хвоста» предоставляет возможность косвенного обнаружения и характеристики массивных скалярных полей вблизи чёрных дыр.

Явление суперрадиации вокруг вращающихся черных дыр может приводить к формированию плотных облаков массивных скалярных полей. В этом процессе, волны, отраженные от эргосферы черной дыры, могут усиливаться, если частота волны меньше частоты вращения черной дыры. Это усиление приводит к экспоненциальному росту плотности скалярного поля вокруг черной дыры, формируя облако, которое значительно влияет на сигнал затухания (ringdown). Наличие этого облака усложняет анализ сигнала ringdown, поскольку вносит дополнительные вклады в его форму и период затухания, затрудняя точное определение параметров черной дыры и массы скалярного поля. Влияние суперрадиации особенно заметно для относительно легких скалярных полей, когда эффект усиления наиболее выражен.

Квазинормальные колебания и затухающие хвосты массивных скалярных возмущений наблюдаются как в случаях без источника, так и при наличии источника, проявляясь в виде исходящих и входящих волновых пакетов.

Численные Исследования Нелинейного Затухания

Для моделирования динамики φ-поля в окрестности чёрной дыры используется метод двойственной нулевой эволюции (Double-Null Evolution). Данный численный метод решения волновых уравнений основан на выборе координат, позволяющих распространять волны вдоль нулевых поверхностей, что обеспечивает эффективное отслеживание динамики поля во времени и пространстве. В рамках этого подхода, временная эволюция φ-поля рассчитывается на дискретной сетке, охватывающей область вокруг чёрной дыры, с использованием численного решения волнового уравнения в выбранной системе координат. Это позволяет исследовать поведение поля при наличии сильных гравитационных полей и отклонений от линейного режима, что невозможно при аналитическом решении.

В основе численного моделирования используется метод конечных разностей, позволяющий дискретизировать дифференциальные уравнения, описывающие эволюцию массивного скалярного поля. Этот подход предполагает замену непрерывных производных конечными разностями, что сводит задачу к решению системы алгебраических уравнений. Дискретизация позволяет эффективно реализовать вычисления на цифровых компьютерах, снижая вычислительную сложность по сравнению с аналитическими методами. Выбор схемы дискретизации и шага по пространству и времени критически важен для обеспечения точности и стабильности численного решения, а также для минимизации ошибок, связанных с дискретизацией $\Delta x$ и $\Delta t$ .

Моделирование эволюции массивного скалярного поля позволяет непосредственно наблюдать и характеризовать отклонения от предсказаний линейной теории возмущений. В рамках данной методики, численное решение уравнений поля выявляет нелинейные эффекты, которые не учитываются в приближении линейной теории. Анализ этих отклонений включает измерение амплитуды, частоты и формы волн, а также исследование их зависимости от параметров системы и начальных условий. Полученные данные используются для проверки точности аналитических моделей и для разработки более совершенных методов описания гравитационных волн и процессов вблизи черных дыр. Отклонения от линейной теории особенно важны при сильных гравитационных полях, где нелинейные эффекты становятся доминирующими.

Численное моделирование эволюции массивных скалярных возмущений для линейного и нелинейных мод демонстрирует отличное соответствие между результатами моделирования и аналитическими предсказаниями, при этом изменение типа начальных данных влияет только на общую амплитуду.

Использование «Игрушечных» Моделей для Анализа Нелинейных Эффектов

Для выделения и анализа нелинейных эффектов используется упрощенная “игрушечная” модель (Toy Model), в которой в качестве источников возбуждения применяются специально подобранные исходящие (Outgoing Wavepackets) и входящие (Ingoing Wavepackets) волновые пакеты. Выбор этих пакетов обусловлен необходимостью контролируемого воздействия на систему и фокусировки на возникающих нелинейных искажениях сигнала. Конкретные параметры волновых пакетов, такие как форма, амплитуда и частотный спектр, тщательно подбираются для максимизации наблюдаемых нелинейных эффектов и минимизации влияния линейных процессов. Это позволяет эффективно изолировать и изучать вклад нелинейных взаимодействий в динамику системы.

Использование упрощенной модели позволяет исследовать поведение сигнала на поздних стадиях временной эволюции. В результате наблюдается возникновение нелинейных степенных хвостов (Nonlinear Power-Law Tails) — участков затухания сигнала, характеризующихся более медленным спадом по сравнению со стандартным Price Tail, описываемым экспоненциальным законом. В отличие от Price Tail, где затухание определяется одним характерным временем, степенные хвосты демонстрируют зависимость амплитуды от времени в виде $t^{-\alpha}$ , где $\alpha > 0$ — показатель степени. Наблюдаемое отклонение от экспоненциального затухания указывает на значимость нелинейных эффектов в формировании поздней динамики сигнала и требует применения специализированных методов анализа для точного определения параметров степенного хвоста.

Метод «Матричный карандаш» (Matrix Pencil Method) применяется для анализа полученного сигнала с целью извлечения частот нелинейных квазинормальных мод (QNMs). В отличие от стандартных QNMs, определяемых линейным спектром оператора, нелинейные взаимодействия изменяют частоты и затухание этих мод. Метод «Матричный карандаш» позволяет точно определить эти измененные частоты, основываясь на анализе сингулярного разложения матрицы, построенной из данных сигнала. Это достигается путем идентификации доминирующих экспоненциальных членов в сигнале, соответствующих различным QNM, и последующего вычисления их комплексных частот. Точность определения частот критична для характеристики степени нелинейности и идентификации источников искажений в динамике системы.

Временная эволюция безмассовых скалярных возмущений демонстрирует различия между исходящими и входящими случаями с движущимся источником по сравнению со случаем без источника.

Значение для Гравитационно-Волновой Астрономии

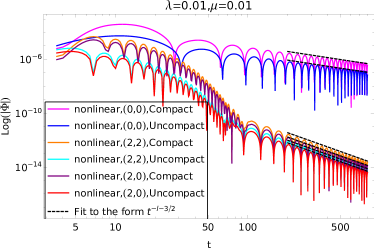
Теория самодействующих скалярных полей предлагает последовательное объяснение возникновения нелинейных квазинормальных мод (QNM) и нелинейных степенных хвостов, наблюдаемых при гравитационном излучении. В рамках этой теории, отклонения от предсказаний линейной теории возмущений возникают из-за взаимодействия скалярных полей с самим собой и с искривленным пространством-временем вокруг черной дыры. $\phi^4$ взаимодействие, в частности, приводит к появлению новых частот в спектре QNM, отличных от тех, что предсказываются в стандартной общей теории относительности. Эти нелинейные эффекты проявляются как изменения в амплитуде и форме сигнала, а также в виде степенных хвостов, затухающих со временем. Анализ этих отклонений, основанный на теории самодействующих скалярных полей, позволяет строить более точные модели гравитационных волн и, потенциально, выявлять признаки новой физики, выходящей за рамки общей теории относительности.

Обнаружение даже незначительных отклонений от предсказаний линейной теории возмущений в данных, получаемых коллаборацией LIGO-Virgo, стало бы убедительным свидетельством существования новой физики, выходящей за рамки общей теории относительности. Анализ гравитационных волн, генерируемых слиянием черных дыр или нейтронных звезд, позволяет с высокой точностью проверять предсказания Эйнштейна. Любые расхождения, особенно в деталях затухания сигнала или в частотах квазинормальных мод, могут указывать на влияние дополнительных полей или модифицированной гравитации. Такие открытия не только расширят наше понимание фундаментальных законов Вселенной, но и откроют новые возможности для исследования природы темной материи, поскольку скалярные поля часто рассматриваются как один из ее вероятных кандидатов.

Исследования, выявляющие нелинейные квазинормальные моды и хвосты в гравитационных волнах, потенциально могут пролить свет на природу тёмной материи. Массивные скалярные поля, являющиеся одним из основных кандидатов на роль этой загадочной субстанции, предсказывают отклонения от стандартной теории гравитации Эйнштейна. Обнаружение этих отклонений, посредством анализа данных, получаемых от коллабораций LIGO-Virgo, предоставит уникальную возможность проверить гипотезы о природе тёмной материи и, возможно, установить связь между гравитационными волнами и фундаментальными свойствами вселенной. Более того, такие исследования позволяют более точно определить параметры скалярных полей, что критически важно для построения реалистичных моделей тёмной материи и понимания её влияния на структуру космоса.

Анализ, проведенный в рамках данной работы, выявил, что квадратичные квазинормальные моды (QNM) возникают с частотами, приблизительно вдвое превышающими частоты их линейных аналогов. Этот результат представляет собой ключевое достижение исследования и подтверждает предсказания теории самовзаимодействующих скалярных полей. Наблюдение таких удвоенных частот QNM в данных, полученных коллаборацией LIGO-Virgo, может стать убедительным доказательством отклонений от общей теории относительности и открыть новые перспективы в понимании природы гравитационных волн. Выявленная закономерность позволяет более точно интерпретировать сигналы от слияния черных дыр и нейтронных звезд, а также способствует развитию новых моделей темной материи, в которых ключевую роль могут играть массивные скалярные поля.

Исследование показало, что отклонения квадратичных квазинормальных мод от удвоенных частот их линейных аналогов не превышают 5%. Этот результат подтверждает высокую точность полученных теоретических предсказаний и служит важным аргументом в пользу обоснованности использованных методов анализа. Такая незначительная погрешность позволяет предполагать, что наблюдаемые в будущем отклонения от стандартной общей теории относительности, связанные с этими модами, будут действительно указывать на наличие новой физики, а не на неточности в моделях. Это, в свою очередь, открывает возможности для более точного поиска и идентификации новых явлений, таких как природа темной материи, используя данные, получаемые от коллабораций LIGO-Virgo.

Исследование демонстрирует, что нелинейные эффекты оказывают незначительное влияние на промежуточные хвосты массивных скалярных возмущений вокруг чёрных дыр. Это не означает, что нелинейность несущественна, скорее, её проявление требует более тонких методов анализа. В связи с этим, особое внимание уделяется квадратичным квазинормальным модам, как потенциальному инструменту для изучения нелинейной динамики. Как однажды заметил Джон Дьюи: «Мы не учимся из опыта, а учимся из отражения над опытом». Данное утверждение применимо и к данной работе: понимание нелинейных эффектов требует не просто регистрации их присутствия, но и глубокого осмысления механизмов, лежащих в их основе, чтобы преобразовать наблюдения в содержательные выводы о природе чёрных дыр и гравитационных волн.

Что дальше?

Представленное исследование, демонстрируя ограниченное влияние нелинейных эффектов на промежуточные «хвосты» массивных скалярных возмущений вокруг чёрных дыр, лишь подчеркивает закономерность: сложная математика часто оказывается лишь изящным описанием простых биологических императивов. В конечном счёте, гравитационные волны — это не просто колебания пространства-времени, а отголоски надежд и страхов, закодированные в движении материи. Поиск квадратичных квазинормальных мод, как потенциального индикатора нелинейной динамики, выглядит как попытка уловить эхо этих первобытных эмоций.

Однако, стоит признать, что даже самые точные модели остаются лишь упрощениями. В реальности, чёрная дыра — это не идеальная сфера, а хаотичное скопление несовершенств. Ограничения численных методов и неполнота теоретического аппарата неизбежно вносят погрешности. Более того, сама концепция «возмущения» может оказаться искусственной, ведь всё во Вселенной взаимосвязано и находится в постоянном движении.

В конечном итоге, понимание гравитационных волн потребует не только совершенствования математических моделей, но и переосмысления фундаментальных принципов, лежащих в основе нашей интерпретации реальности. Ведь всё поведение — это всего лишь баланс между страхом и надеждой, а уравнения могут лишь приблизительно отразить эту сложную динамику.

Оригинал статьи: https://arxiv.org/pdf/2601.16016.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-25 11:47