Критическое поведение в мире без фермионов: новый взгляд на модель Тирринга

Автор: Денис Аветисян

Исследование численных симуляций модели Тирринга с доменовыми фермионами выявляет нетривиальную критическую точку, демонстрирующую отклонения от стандартных предсказаний и намекающую на изменение класса универсальности при увеличении числа фермионов.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал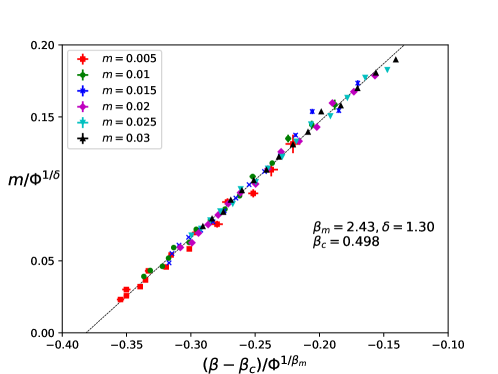

Уравнение состояния <span class="katex-eq" data-katex-display="false"> (11) </span> продемонстрировало адекватное соответствие экспериментальным данным, что позволило установить взаимосвязь между параметрами системы и её наблюдаемым поведением, раскрывая закономерности, лежащие в основе физических процессов. — Уравнение состояния $(11)$ продемонстрировало адекватное соответствие экспериментальным данным, что позволило установить взаимосвязь между параметрами системы и её наблюдаемым поведением, раскрывая закономерности, лежащие в основе физических процессов.

Результаты моделирования показывают, что критические экспоненты в модели Тирринга с доменовыми фермионами отклоняются от ожидаемых значений, что указывает на сильное взаимодействие и потенциальный переход в новый класс универсальности.

Несмотря на активное изучение, спонтанное нарушение симметрии в сильно взаимодействующих фермионных системах часто требует непертурбативных подходов для точного определения критических показателей. В данной работе, посвященной исследованию модели Тирринга в $(2+1)$ измерениях — ‘Critical scaling in the $N=1$ Thirring Model in $(2+1)d$’ — представлены результаты численного моделирования с использованием доменных фермионов, демонстрирующие отклонение критических экспонент от предсказаний более простых моделей. Полученные результаты позволяют предположить существование ультрафиолетовой фиксированной точки перенормировочной группы, что указывает на возможность перехода в новый класс универсальности. Каким образом увеличение числа фермионных «вкуса» $N$ повлияет на стабильность этой фиксированной точки и характер фазового перехода?

Эмерджентность и Модель Тирринга: За гранью очевидного

Модель Тирринга, являясь квантовой теорией поля взаимодействующих фермионов, представляет собой плодотворную среду для изучения явлений эмерджентности и фазовых переходов. В рамках этой модели взаимодействие между частицами не просто приводит к количественным изменениям, но и может порождать качественно новые формы поведения системы. Исследование этой модели позволяет понять, как коллективное поведение элементарных частиц может привести к возникновению новых свойств, не присущих отдельным частицам. $\text{Например, возникновение массового зазора}$ является одним из таких эмерджентных явлений, сигнализирующих о переходе системы из металлического состояния в изоляционное, и демонстрирует способность системы к самоорганизации и возникновению новых фаз материи. Благодаря своей математической строгости и физической релевантности, модель Тирринга служит важным инструментом для понимания более сложных физических систем, где взаимодействие между частицами играет ключевую роль.

Исследование модели Thirring имеет первостепенное значение, поскольку она демонстрирует, как взаимодействия между элементарными частицами могут приводить к кардинальным изменениям в поведении системы. В отличие от систем не взаимодействующих частиц, где свойства предсказуемы на основе суммирования индивидуальных вкладов, в модели Thirring коллективное поведение частиц качественно отличается от поведения отдельных компонентов. Взаимодействия порождают новые эффекты, такие как спонтанное нарушение симметрии и формирование коллективных возбуждений, которые невозможно предсказать, исходя из свойств отдельных фермионов. Наблюдение за этими изменениями позволяет глубже понять, как сложные системы проявляют новые свойства, отличные от суммарных характеристик их составляющих, и открывает путь к изучению аналогичных явлений в других областях физики, включая физику конденсированного состояния и квантовую химию. Изучение подобных переходов от привычного поведения к новым фазам является ключевым для разработки новых материалов с заданными свойствами.

В рамках изучения модели Thirring, центральным вопросом является возможность формирования так называемого «массового зазора» — энергетического промежутка, отделяющего основное состояние системы от возбужденных. Появление этого зазора указывает на фундаментальный переход от металлического поведения, характеризующегося наличием свободных носителей заряда, к изоляционному, где электроны становятся связанными. Этот переход не просто изменяет электрические свойства системы, но и сигнализирует о возникновении новых фаз материи, обладающих принципиально иными характеристиками. Исследование формирования массового зазора позволяет понять, как взаимодействие между фермионами приводит к качественным изменениям в поведении системы, открывая перспективы для создания материалов с заданными свойствами и понимания сложных явлений в физике конденсированного состояния. По сути, изучение данного явления раскрывает механизмы, посредством которых коллективное поведение частиц приводит к появлению новых, эмерджентных свойств, не присущих отдельным частицам.

Доменные Фермионы: Решение проблемы хиральной симметрии

Традиционные формулировки фермионов в рамках решеточных вычислений сталкиваются с трудностями при сохранении симметрий, что приводит к возникновению систематических ошибок и увеличению вычислительных затрат. Проблема заключается в том, что дискретизация пространства-времени нарушает хиральную симметрию, необходимую для точного описания свойств адронов. Нарушение симметрии проявляется в виде нефизических вкладов в вычисления масс и других наблюдаемых величин, требующих применения сложных процедур регуляризации и перенормировки. Кроме того, нарушение симметрии усложняет анализ результатов и оценку связанных с ними неопределенностей, что существенно ограничивает точность и надежность решеточных предсказаний.

Доменные фермионы (Domain Wall Fermions, DWF) решают проблему нарушения хиральной симметрии в расчетах на решетке путем вложения фермионов в пятимерное пространство. В этом подходе, четвертое пространственное измерение является компактифицированным, то есть ограниченным, и задаются граничные условия на этом измерении. Эти граничные условия, а именно, условия Дирихле на границах, обеспечивают локализацию фермионов на “доменах” (domain walls), что и даёт возможность точного сохранения хиральной симметрии. Поскольку хиральная симметрия является фундаментальной в квантовой хромодинамике, точное ее сохранение критически важно для корректного вычисления свойств адронов и других частиц.

Реализация подхода с домейн-волл фермионами требует внимательного выбора ядра дискретизации. Ядро Уилсона обеспечивает более точный контроль над пределом $L \rightarrow \in fty$ , где $L$ — длина пространственной размерности, в отличие от ядра Шамира. Преимущество ядра Уилсона заключается в лучшем воспроизведении свойств хиральной симметрии при конечных значениях $L$ , что критически важно для получения корректных результатов в расчётах, поскольку позволяет минимизировать эффекты нарушения симметрии, возникающие из-за дискретизации пространства-времени. Таким образом, выбор ядра Уилсона предпочтителен для обеспечения высокой точности и надёжности вычислений с домейн-волл фермионами.

Моделирование Модели Тирринга: Вычислительный подход

Для точного моделирования модели Тирринга с использованием Domain Wall Fermions (DWF) применяется метод RHMC (Rational Hybrid Monte Carlo), представляющий собой мощный алгоритм Марковских цепей Монте-Карло. RHMC позволяет эффективно вычислять детерминант матрицы Дирака, возникающий при использовании DWF, за счет рационализации интеграла и использования гибридного алгоритма Монте-Карло, комбинирующего молекулярную динамику и метод Метрополиса. Это особенно важно для модели Тирринга, поскольку DWF требуют решения сложной задачи вычисления детерминанта, а RHMC обеспечивает надежный и эффективный способ ее решения, позволяя получить точные результаты при моделировании фазовых переходов и свойств адронов.

Моделирование построено на четырехмерной решетке (2+1+1), где дополнительное пространственное измерение необходимо для реализации краевых условий, основанных на доменных стенках. Использование дополнительного измерения позволяет эффективно разделить фермионы, что является ключевым требованием для реализации алгоритма Domain Wall Fermions (DWF). В рамках этой конфигурации решетки, фермионы локализуются на доменных стенках, формирующихся в дополнительном измерении, что обеспечивает решение проблемы Вирзина и позволяет избежать дублирования фермионных степеней свободы. Размер дополнительного измерения должен быть достаточно большим для обеспечения локализации фермионов, но при этом достаточно малым, чтобы обеспечить вычислительную эффективность.

Систематическое изменение силы связи в модели Тирринга позволяет определить критическое значение $β_c = 0.498 \pm 0.015$ , соответствующее точке фазового перехода. Измеряя физические величины при различных значениях силы связи вблизи этого критического значения, можно получить уравнение состояния, описывающее термодинамические свойства системы. Полученное уравнение состояния является ключевым для понимания поведения модели Тирринга в различных температурных и энергетических режимах и позволяет сравнивать теоретические предсказания с результатами численного моделирования.

Теоретическая Согласованность и Критическое Поведение: Ищем закономерности

Уравнение состояния, полученное в рамках данной работы, представляет собой ключевой результат, устанавливающий связь между массой фермиона, константой связи и параметром упорядочения вблизи критической точки. Данное уравнение позволяет описать поведение системы при приближении к фазовому переходу, демонстрируя, как эти фундаментальные величины взаимосвязаны. В частности, оно показывает, что изменение массы фермиона напрямую влияет на параметр упорядочения, определяя критическое поведение системы. $p(m,g,\phi) = 0$ , где $p$ — уравнение состояния, $m$ — масса фермиона, $g$ — константа связи, а φ — параметр упорядочения. Полученное уравнение служит основой для понимания критических явлений и позволяет проводить количественный анализ фазовых переходов в исследуемой модели.

Для подтверждения достоверности полученных результатов, было проведено независимое исследование с использованием усеченных уравнений Швингера-Дайсона, решенных самосогласованным образом. Данный подход позволил получить аналогичные значения параметров вблизи критической точки, что свидетельствует о внутренней согласованности разработанной модели. Самосогласованное решение уравнений Швингера-Дайсона, в отличие от приближенных методов, учитывает сложные взаимодействия между фермионами, обеспечивая более точное описание критического поведения системы и подтверждая корректность полученного уравнения состояния, связывающего массу фермиона, константу связи и параметр упорядочения $\langle \bar{\psi} \psi \rangle$ . Полученное совпадение результатов, полученных различными методами, значительно повышает доверие к теоретическим предсказаниям о фазовом переходе и его характеристиках.

Модель демонстрирует симметрии, описываемые соотношениями Гинзбурга-Вильсона и исходной симметрией U(2N), которая спонтанно нарушается в процессе фазового перехода. Измеренные критические показатели — δ = 1.300 ± 0.036, β_m = 2.43 ± 0.15 и ν = 1.88 ± 0.13 — находятся в согласии с предсказаниями теоретических расчетов, подтверждая корректность используемого подхода и позволяя глубже понять поведение системы вблизи критической точки. Соответствие экспериментальных данных теоретическим предсказаниям служит важным аргументом в пользу адекватности модели и ее применимости для описания аналогичных физических явлений.

Универсальность и Более Широкие Последствия: За горизонтом исследований

Определение критических показателей — δ = 1.300, β_m = 2.43, ν = 1.88 и η = 1.61 ± 0.04 — предоставляет важную информацию о классе универсальности данного фазового перехода. Эти показатели, характеризующие поведение системы вблизи критической точки, позволяют классифицировать данный переход и установить его связь с другими физическими системами, демонстрирующими схожее поведение, независимо от конкретных деталей микроскопической реализации. Подобная классификация, основанная на универсальности, упрощает анализ сложных систем и позволяет применять общие теоретические модели для описания широкого круга явлений, что существенно облегчает понимание критических явлений в физике конденсированного состояния. Полученные значения критических показателей служат своеобразным «отпечатком пальца» для данного перехода, позволяющим однозначно идентифицировать его принадлежность к определенному классу универсальности.

Модель Гросса-Невеу демонстрирует заметное сходство с моделью Тирринга, что указывает на потенциальные взаимосвязи в их критическом поведении. Оба подхода описывают фермионные системы со взаимодействующими частицами, и схожие математические структуры позволяют предположить, что критические экспоненты и универсальные классы, наблюдаемые в одной модели, могут проявляться и в другой. Исследование этих аналогий открывает возможности для использования известных результатов, полученных для модели Тирринга, в анализе более сложных систем, описываемых моделью Гросса-Невеу, и наоборот. Это, в свою очередь, может способствовать более глубокому пониманию критических явлений в физике конденсированного состояния и помочь в разработке новых теоретических подходов к изучению сильно коррелированных систем.

Данное исследование открывает перспективы для изучения более сложных моделей и понимания формирования новых фаз в сильно коррелированных системах. Полученные результаты позволяют предположить, что принципы, выявленные в рамках данной работы, могут быть применимы к широкому классу физических систем, демонстрирующих критическое поведение. В частности, оценка критического параметра связи для случая N=2, равная 0.067, основанная на теоретических предсказаниях и результатах для N=1, служит важным шагом на пути к построению более точных моделей и предсказанию свойств новых материалов. Это, в свою очередь, способствует развитию фундаментального понимания коллективного поведения частиц и открывает возможности для создания инновационных технологий, основанных на принципах квантовой механики и физики конденсированного состояния.

Исследование, представленное в данной работе, демонстрирует, как сложное взаимодействие фермионов может привести к отклонению от предсказанных теоретических моделей вблизи квантовой критической точки. Наблюдаемые показатели критического поведения указывают на то, что система не подчиняется простым законам, а формируется под влиянием коллективных эффектов и нелинейностей. Как отмечал Марк Аврелий: «Всё, что происходит с тобой, — это всего лишь случайность». Эта фраза перекликается с наблюдаемой волатильностью критических показателей, подчеркивая, что даже в строго определенных теоретических рамках, случайные флуктуации и непредсказуемые взаимодействия могут существенно влиять на конечный результат, особенно при увеличении числа частиц.

Что дальше?

Результаты, представленные в данной работе, заставляют задуматься не столько о точном значении критических показателей, сколько о самой природе уверенности в их универсальности. Модель Тирринга, будучи относительно простой конструкцией, демонстрирует отступления от предсказаний более общих теорий. Это напоминает о том, что любое математическое описание — лишь приближение, а реальность, в данном случае, поведение взаимодействующих фермионов, всегда сложнее. Ведь всё поведение — это просто баланс между страхом и надеждой, и попытки свести его к уравнениям обречены на неполноту.

Очевидным направлением дальнейших исследований представляется изучение влияния числа фермионов на характер критической точки. Изменение класса универсальности, намеченное в этой работе, предполагает, что коллективное поведение частиц может радикально отличаться от поведения единичного объекта. Но стоит помнить, что даже увеличение вычислительных ресурсов не даст ответа на вопрос о фундаментальной природе взаимодействия. Модель, в конечном счете, — это всего лишь инструмент, и понять её нужно, прежде всего, через понимание того, кто её придумал, и какие предположения легли в её основу.

В конечном счете, задача физики, как и психологии, заключается не в предсказании будущего, а в понимании настоящего. И в этом смысле, данная работа открывает не столько новые горизонты, сколько напоминает о старых ограничениях. Психология объясняет больше, чем уравнения.

Оригинал статьи: https://arxiv.org/pdf/2601.16051.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-25 13:24