Автор: Денис Аветисян
Новое исследование демонстрирует, как неабелевы статистики, ключевые для топологических квантовых вычислений, проявляются в сложных многочастичных состояниях.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал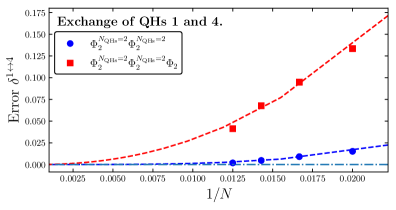
Представлен метод извлечения матриц переплетения для систем до 80 частиц, подтверждающий дуальность уровня и ранга и данные о переплетении аньонов Фибоначчи.
Квантовые системы с частицами, демонстрирующими неабелеву статистику обмена, представляют собой сложную задачу для теоретического описания и экспериментальной реализации. В работе ‘Non-Abelian fusion and braiding in many-body parton states’ разработан метод построения волновых функций для широкого класса неабелевых состояний дробного квантового эффекта Холла, основанный на партонном подходе. Полученные результаты позволяют вычислить матрицы переплетения для систем до 80 частиц, подтверждая дуальность уровня и ранга, а также демонстрируя свойства переплетения для анионов Фибоначчи. Сможет ли предложенный подход стать основой для диагностики и классификации неабелевых состояний в экспериментально наблюдаемых дробных квантовых эффектах Холла?
За гранью Ландау: Эхо Дробных Состояний
Дробный квантовый эффект Холла демонстрирует существование экзотических состояний материи, принципиально отличающихся от тех, что описываются в рамках традиционных представлений об отдельных частицах. В этих состояниях электроны коллективно взаимодействуют, формируя новые квазичастицы с дробным электрическим зарядом и необычными статистическими свойствами. Вместо поведения независимых частиц, система проявляет согласованное поведение, где коллективные эффекты доминируют над индивидуальными. Это означает, что привычные представления о проводимости и сопротивлении материалов становятся неприменимы, открывая путь к совершенно новым материалам с уникальными электронными свойствами и потенциальными применениями в передовых технологиях. Исследование этих состояний требует пересмотра фундаментальных концепций физики конденсированного состояния и разработки новых теоретических моделей, способных адекватно описать коллективное поведение электронов в сильных магнитных полях и при низких температурах.
В дробном квантовом эффекте Холла обнаружены состояния материи, демонстрирующие дробный электрический заряд и необычную статистику частиц, что кардинально отличается от представлений классической физики конденсированного состояния. Вместо привычных целых значений заряда, электроны в этих состояниях ведут себя так, будто несут лишь часть элементарного заряда, например, e/3 или e/5. Более того, обмен двумя частицами в этих состояниях может приводить не к простому изменению знака волновой функции, как в случае бозонов и фермионов, а к более сложным преобразованиям, определяемым анионной статистикой. Это означает, что частицы ведут себя как квазичастицы с дробными свойствами, а их коллективное поведение существенно отличается от предсказаний стандартной теории, требуя разработки новых теоретических моделей для объяснения наблюдаемых феноменов и понимания фундаментальных свойств этих экзотических состояний материи.
Традиционная теория Ландау, успешно описывающая целочисленный квантовый эффект Холла, оказывается недостаточной для объяснения дробного квантового эффекта Холла. В то время как теория Ландау рассматривает электроны как не взаимодействующие частицы, движущиеся в магнитном поле, дробный эффект Холла демонстрирует коллективное поведение электронов, формирующих новые квазичастицы с дробным зарядом и необычными статистическими свойствами. Поэтому, для адекватного описания этого явления необходимы принципиально новые теоретические подходы, такие как теория составных фермионов и иерархические модели, учитывающие сложные взаимодействия между электронами и формирование новых степеней свободы. Эти модели позволяют объяснить наблюдаемые дробные значения проводимости и предсказывают существование экзотических состояний материи, не имеющих аналогов в обычной физике конденсированного состояния.
Поиск устойчивых, неабелевых состояний в рамках эффекта дробного квантового Холла является ключевой целью для развития топологических квантовых вычислений. В отличие от традиционных кубитов, подверженных декогеренции из-за взаимодействия с окружающей средой, неабелевы квазичастицы, возникающие в некоторых дробных квантовых состояниях, обладают уникальной устойчивостью. Информация кодируется не в отдельных частицах, а в их топологическом переплетении, что делает вычисления невосприимчивыми к локальным возмущениям. Специфические состояния, такие как \nu = 5/2 , представляют особый интерес, поскольку теоретически поддерживают майорановские фермионы — квазичастицы, являющиеся собственными античастицами, что потенциально позволяет создавать отказоустойчивые квантовые компьютеры. Исследования направлены на точное обнаружение и манипулирование этими состояниями в гетероструктурах из полупроводниковых гетероструктур, что представляет собой сложную задачу, требующую прецизионного контроля над материалами и внешними условиями.
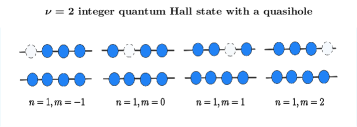
Разложение Электронов: Искусство Партонов
Теория партонов представляет собой принципиально новый подход к описанию взаимодействующих электронов в конденсированных средах. Вместо рассмотрения электронов как отдельных частиц, она постулирует, что система может быть эквивалентно описана как совокупность квазичастиц — партонов — несущих дробный электрический заряд. Это означает, что каждый электрон может «фрагментироваться» на несколько партонов, каждый из которых имеет заряд, равный, например, e/3 или e/5, где e — элементарный электрический заряд. Такой подход позволяет упростить расчеты сложных многочастичных систем, представляя взаимодействие как взаимодействие квазичастиц с более простыми свойствами, чем у исходных электронов. Идея заключается в том, что коллективное поведение этих дробно заряженных квазичастиц воспроизводит поведение исходных электронов.
Для упрощения решения многочастичной задачи в рамках теории партонов используется концепция псевдо-уровней Ландау. В отличие от истинных уровней Ландау, формирующихся под действием внешнего магнитного поля, псевдо-уровни Ландау возникают из-за сильных кулоновских взаимодействий между электронами в двумерной электронной системе. Эти взаимодействия приводят к перестройке энергетического спектра и образованию дискретных уровней, эффективно уменьшая степень свободы системы. Эффективное описание, основанное на псевдо-уровнях Ландау, позволяет аппроксимировать сложное многочастичное взаимодействие, упрощая вычисления и позволяя получить аналитические решения для некоторых свойств системы, например, для энергии основного состояния и корреляционных функций. \omega_c = \frac{eB}{m} — частота циклотронного резонанса, где e — заряд электрона, B — магнитное поле, m — масса электрона.
Теория Черна-Симонса предоставляет естественную основу для описания эффективной теории поля этих партонов. В контексте фракционированных возбуждений, таких как в квантовых эффектах Холла, теория Черна-Симонса позволяет построить лагранжиан, описывающий динамику партонов как безмассовых частиц, взаимодействующих через калиточное поле. \mathcal{L} = \frac{1}{4\pi} \epsilon^{\mu\nu\rho} A_\mu \partial_\nu A_\rho — типичный пример лагранжиана, где A_\mu — калиточное поле, а \epsilon^{\mu\nu\rho} — полностью антисимметричный тензор Леви-Чивиты. Данный подход позволяет аналитически исследовать свойства системы и предсказывать наблюдаемые физические величины, такие как проводимость и магнитная восприимчивость, в терминах коллективных возбуждений партонов.
Состояние целочисленного квантового эффекта Холла (ЦКЭХ) служит основой для построения волновых функций партонов. В ЦКЭХ, система взаимодействующих электронов в двумерном электронном газе подвергается сильному магнитному полю, приводящему к квантованию кинетической энергии и образованию ландауровских уровней. Волновая функция ЦКЭХ, описывающая заполненные ландауровские уровни, представляет собой произведение одночастичных волновых функций, локализованных в определенных областях пространства. Эта структура позволяет использовать ее в качестве отправной точки для построения волновых функций, описывающих системы партонов, где электроны «фрагментируются» на квазичастицы с дробным зарядом и статистикой.
Анионы и Заплетения: Танец Неабелевой Статистики
Аньоны — это квазичастицы, проявляющие статистику, отличную от бозонной и фермионной. В то время как бозоны и фермионы подчиняются целочисленной статистике, определяемой спином, аньоны характеризуются дробной статистикой, где фазовый сдвиг при обмене двумя частицами не равен ни 0, ни π. Это означает, что при перестановке двух аньонов волновой функции частицы претерпевает изменение, которое не соответствует стандартным квантовым механическим правилам для бозонов или фермионов. Существование аньонов является ключевым признаком экзотических состояний материи, таких как дробный квантовый эффект Холла, и требует для своего описания более сложных математических моделей, чем те, которые применимы к обычным частицам.
Неабелева статистика, проявляемая определенными типами анионов, предполагает, что обмен позициями двух частиц не просто приводит к фазовому сдвигу волновой функции, как в случае бозонов или фермионов, а осуществляет некоммутативную операцию, изменяющую квантовое состояние системы. В отличие от абелевой статистики, где порядок обмена частиц не имеет значения, для неабелевых анионов порядок обмена принципиален и определяет конечный квантовый вид состояния. Данное преобразование, известное как «заплетение» (braiding), описывается матрицами, отражающими некоммутативность операций обмена, и позволяет кодировать и манипулировать квантовой информацией принципиально новым способом, отличным от традиционных кубитов.
Матрица заплетения — это математический инструмент, описывающий изменение квантового состояния при обмене двумя анионами. В отличие от бозонов и фермионов, обмен анионами не приводит к простому умножению на +1 или -1; вместо этого, матрица плетения представляет собой унитарный оператор, который преобразует исходное состояние в новое. Элементы этой матрицы зависят от траектории обмена анионами и отражают некоммутативность операций обмена, что является ключевым свойством неабелевой статистики. Таким образом, матрица плетения полностью характеризует статистические свойства анионов и позволяет предсказывать эволюцию многочастичной системы.
Высокопроизводительные вычислительные ресурсы, такие как суперкомпьютер Nandadevi, позволили численно рассчитать матрицы заплетения для систем, содержащих до N=80 частиц. Эти вычисления, основанные на моделировании сложных квантовых систем, подтверждают теоретические предсказания о неабелевой статистике любогонов и позволяют верифицировать корректность используемых теоретических моделей. Полученные матрицы заплетения служат прямым доказательством существования нетривиальных фаз материи, характеризующихся топологической защитой квантовой информации, и открывают перспективы для создания устойчивых квантовых вычислительных устройств.
Состояния Мура-Резайи и Теория Конформного Поля: Математический Ландшафт
Состояние Мура-Резайи, являющееся ярким примером неабелевой фазы, представляет особый интерес в физике конденсированного состояния благодаря своей способности поддерживать неабелевы энионы — квазичастицы с необычными статистическими свойствами. Построение этого состояния базируется на концепции композитных фермионов, возникающих из электронов, взаимодействующих с магнитным полем, что приводит к формированию новых квазичастиц с дробным зарядом и необычными статистическими свойствами. Эти неабелевы энионы, благодаря их топологической защите, могут служить строительными блоками для устойчивых квантовых вычислений. Исследование состояния Мура-Резайи служит отправной точкой для изучения более общих неабелевых состояний и понимания фундаментальных аспектов топологического порядка в конденсированных системах.
Состояния Рида-Резайи представляют собой обобщение концепции состояния Мура-Рида, образуя целое семейство волновых функций, параметризованных числом k. В отличие от фиксированного состояния Мура-Рида, которое соответствует конкретному значению k=2, семейство Рида-Резайи позволяет исследовать различные топологические фазы материи, варьируя параметр k. Каждое значение k определяет специфическую структуру дробных квантовых эффектов и свойства экзотических квазичастиц — анионов. Исследование этих состояний с различными k позволяет глубже понять связь между топологическим порядком, свойствами анионов и потенциальными приложениями в квантовых вычислениях.
Теория конформного поля парафермионов предоставляет мощный математический аппарат для описания волновых функций состояний Read-Rezayi. Эти состояния, характеризующиеся сложной структурой, обусловленной наличием неабелевых энионов, описываются с помощью корреляционных функций. Данный подход упрощает анализ их свойств и поведения, позволяя проводить точные вычисления и предсказывать наблюдаемые физические явления. Он также позволяет изучать топологическую защиту квантовой информации, которая является ключевым фактором для создания устойчивых квантовых компьютеров.
Численные расчеты, направленные на изучение состояний Read-Rezayi, выявили незначительные расхождения между полученными матрицами заплетения и теоретическими предсказаниями. Эти расхождения уменьшаются с увеличением числа частиц в рассматриваемой системе, что говорит о том, что они связаны с конечным размером системы. Результаты подтверждают перспективность численных методов для верификации теоретических моделей экзотических состояний материи и углубленного понимания свойств неабелевых энионов.
Двойственность и Будущие Направления: К Надежным Топологическим Квантовым Вычислениям
Двойственность уровня и ранга представляет собой мощный инструмент, позволяющий установить связь между теориями Черна-Симонса с различными параметрами, открывая новые перспективы в понимании дробного квантового эффекта Холла (FQHE). Этот математический подход позволяет рассматривать различные состояния FQHE как эквивалентные, что упрощает анализ и предсказание их свойств. Использование двойственности позволяет переходить от сложных состояний к более простым, сохраняя при этом физически важные характеристики, такие как топологический порядок и типы анионов, что открывает возможности для разработки новых материалов и устройств.
Понимание взаимодействия между различными квантовыми состояниями дробного квантового эффекта Холла (FQHE) и связанными с ними анионами является ключевым для создания устойчивых квантовых вычислений. Различные состояния FQHE характеризуются уникальными типами анионов, которые могут служить кубитами для квантовых вычислений, обеспечивая защиту от ошибок. Исследование способов манипулирования этими анионами, их запутывания и реализации квантовых вентилей требует глубокого понимания их взаимодействия в различных состояниях FQHE. Успешная реализация надежных квантовых вычислений напрямую зависит от способности контролировать и использовать эти фундаментальные свойства анионов.
Численные расчеты показали, что ранг пространства фьюзий для состояний Фрацона Холла с заполнениями ν = 2/2, 2/3 и для спроецированных состояний соответствует предсказаниям конформной теории поля. Данное соответствие подтверждает теоретические модели, описывающие коллективное поведение квазичастиц в этих системах. Ранг пространства фьюзий определяет число различных способов, которыми могут сливаться анионы, и его соответствие теоретическим расчетам подтверждает, что эти состояния действительно поддерживают экзотические возбуждения, необходимые для топологических квантовых вычислений.
Перспективные исследования в области топологических квантовых вычислений направлены на поиск и создание материалов, способных поддерживать экзотические любыеоны. Разработка устройств, позволяющих контролировать и манипулировать этими любыонами, представляет собой ключевую задачу. Ученые активно изучают гетероструктуры двумерных электронных систем, такие как квантовые ямы и гетероструктуры на основе графена, в надежде обнаружить условия, благоприятствующие формированию и стабильности этих частиц. Параллельно ведется разработка наноэлектронных устройств, способных создавать, перемещать и взаимодействовать с любыонами, что откроет путь к реализации масштабируемых и надежных квантовых компьютеров нового поколения.
В исследовании неабелевых фьюзий и плетения в многочастичных партонных состояниях отчетливо прослеживается закономерность, напоминающая о сложности и непредсказуемости систем. Подобно тому, как природа сама по себе склонна к самоорганизации и возникновению неожиданных свойств, так и эта работа демонстрирует, что попытки жесткого контроля над поведением частиц обречены на провал. Ричард Фейнман однажды заметил: «Если вы думаете, что понимаете квантовую механику, значит, вы её не понимаете». В данном исследовании, сложность описания взаимодействия множества частиц, даже при стремлении к точному математическому моделированию, подчеркивает эту мысль. Изучение плетения анионов, как и любое построение сложной системы, — это не прямолинейный процесс, а скорее эволюция, в которой необходимо учитывать не только текущее состояние, но и потенциальные траектории развития.
Что дальше?
Представленные методы демонстрации неабелевой статистики в партонных состояниях, несомненно, расширяют инструментарий для изучения топологических фаз материи. Однако, следует признать, что извлечение матриц переплетения для столь большого числа частиц — это не победа над хаосом, а лишь его временное укрощение. Каждая архитектурная деталь, каждый выбор базиса неминуемо несёт в себе пророчество о будущем сбое, о той точке, где вычислительные ресурсы окажутся недостаточны для поддержания иллюзии стабильности. Гарантий здесь нет, лишь договор с вероятностью.
Более того, успешная проверка двойственности уровня-ранга и данных, соответствующих аньонам Фибоначчи, — это лишь первый шаг. Реальные системы, конечно, далеки от идеализированных моделей. Важно понимать, что флуктуации, взаимодействие с окружением и несовершенство материалов неизбежно внесут свои коррективы. Стабильность — это просто иллюзия, которая хорошо кэшируется, но рано или поздно её память стирается.
Поэтому, следующим этапом представляется не столько увеличение числа частиц в моделируемой системе, сколько разработка методов, устойчивых к шумам и несовершенствам. Поиск новых топологических фаз, способных выдержать более суровые условия реального мира, — вот куда должна быть направлена основная энергия. Системы — это не инструменты, а экосистемы. Их нельзя построить, только вырастить.
Оригинал статьи: https://arxiv.org/pdf/2601.16819.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Все рецепты культистского круга в Escape from Tarkov
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Решение головоломки с паролем Absolum в Yeldrim.
- Лучшие транспортные средства в Far Cry 6
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Необходимо: Как выращивать урожай
- Где найти и поймать бабочку Солнечного луча в Палии
- Dragon’s Dogma 2: Где найти Драконорожденных
- All Valley Pass Aurylene Locations In Endfield
- Как получить скины Alloyed Collective в Risk of Rain 2
2026-01-26 14:46