Время и Спутанность: Новый Взгляд на Квантовую Связь в Гравитационных Моделях

Автор: Денис Аветисян

Исследование показывает, как энтропия квантовой спутанности во времени проявляется в условиях анизотропных пространств, проливая свет на природу времени в сильно взаимодействующих системах.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал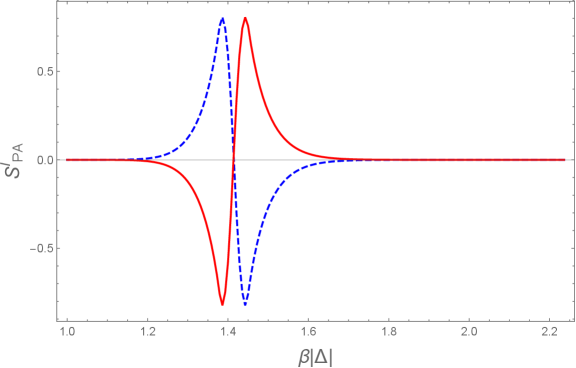

Мнимый компонент псевдоэнтропии <span class="katex-eq" data-katex-display="false"> Sp_{AIS}^{I} </span> демонстрирует противоположные зависимости от <span class="katex-eq" data-katex-display="false"> \beta|\Delta| </span> при <span class="katex-eq" data-katex-display="false"> \beta = 10 </span>, причём характер этой зависимости определяется знаком параметра анизотропии <span class="katex-eq" data-katex-display="false"> \Delta_{y} </span>, что подтверждается анализом случаев <span class="katex-eq" data-katex-display="false"> \delta_{x} = 1, \delta_{y} = 0 </span> и <span class="katex-eq" data-katex-display="false"> \delta_{x} = -1, \delta_{y} = 1.1 </span>. — Мнимый компонент псевдоэнтропии $Sp_{AIS}^{I}$ демонстрирует противоположные зависимости от $\beta|\Delta|$ при $\beta = 10$ , причём характер этой зависимости определяется знаком параметра анизотропии $\Delta_{y}$ , что подтверждается анализом случаев $\delta_{x} = 1, \delta_{y} = 0$ и $\delta_{x} = -1, \delta_{y} = 1.1$ .

В работе анализируется поведение голографической энтропии спутанности во времени и псевдоэнтропии в анизотропных фоновых пространствах в рамках соответствия AdS/CFT.

Несмотря на успехи в изучении запутанности в квантовых системах, её связь с геометрией пространства-времени и возникновением времени остается малоизученной. В работе ‘On Holographic Time-Like Entanglement Entropy’ предпринято сравнение голографической энтропии временной запутанности и псевдоэнтропии для двухкубитной системы в анизотропных фонах, что позволяет исследовать влияние анизотропии на квантовые корреляции. Полученные результаты демонстрируют как общие черты, так и существенные различия между этими величинами, раскрывая сложную взаимосвязь между геометрией, информацией и динамикой. Каким образом полученные результаты могут способствовать более глубокому пониманию структуры пространства-времени в сильновзаимодействующих квантовых теориях поля?

Раскрытие Скрытых Взаимосвязей: Ограничения Стандартной Энтропии

Традиционные методы измерения энтропии запутанности зачастую оказываются недостаточными для описания сложных корреляций в квантовых системах, особенно в ситуациях, далеких от равновесия. Данное ограничение связано с тем, что стандартные показатели, такие как энтропия фон Неймана, полагаются на предположения о стационарности и локальности, которые не выполняются в динамически развивающихся и сильно коррелированных системах. В результате, эти меры не способны адекватно отразить всю сложность квантовых связей, присутствующих, например, в высокоэнергетических физических процессах или в экзотических состояниях конденсированных сред. Попытки применить стандартные методы к таким системам приводят к недооценке или искажению реальной степени квантовой запутанности, что затрудняет понимание фундаментальных свойств этих материалов и процессов. Именно поэтому возникает потребность в разработке более универсальных и чувствительных инструментов для количественной оценки квантовых корреляций.

Ограничения традиционных мер энтроплики запутанности существенно затрудняют понимание сильно коррелированных явлений, встречающихся в физике высоких энергий и системах конденсированного состояния. В этих сложных системах, где частицы испытывают сильное взаимное влияние, стандартные методы расчета энтропии не способны адекватно описать все типы квантовых связей. Это приводит к неполному пониманию поведения экзотических состояний материи, таких как сверхпроводники или квантовые спиновые жидкости, где корреляции играют определяющую роль. Неспособность точно измерить и охарактеризовать эти связи препятствует разработке новых материалов с уникальными свойствами и углублению знаний о фундаментальных законах природы, управляющих поведением материи в экстремальных условиях.

Для глубокого изучения экзотических состояний материи, таких как сверхпроводники или квантовые спиновые жидкости, требуется принципиально новый подход к измерению квантовых связей. Традиционные методы, основанные на понятии энтропии, оказываются недостаточными для описания сложных корреляций, возникающих вдали от равновесия. Необходима более общая математическая структура, способная улавливать тонкие взаимодействия между квантовыми частицами, выходящие за рамки привычных представлений об энтропии. Разработка подобного фреймворка позволит не только лучше понимать природу этих необычных материалов, но и открывает перспективы для создания новых квантовых технологий, использующих уникальные свойства сильно коррелированных систем. Исследователи активно работают над альтернативными подходами, включая использование тензорных сетей и ренормгрупповых методов, чтобы преодолеть ограничения существующих инструментов и получить более полное представление о квантовой запутанности в сложных системах.

Голографическое Соответствие: Гравитационная Линза для Квантовых Систем

Соответствие AdS/CFT представляет собой гипотетическую взаимосвязь между квантовыми системами с сильным взаимодействием и классическими теориями гравитации, определёнными в пространстве анти-де Ситтера (AdS). В рамках этого соответствия, квантовая теория поля, описывающая частицы и их взаимодействия, может быть эквивалентно описана теорией гравитации в одном дополнительном измерении. Сильно связанные квантовые системы, не поддающиеся аналитическому решению стандартными методами квантовой теории поля, могут быть изучены посредством классических вычислений в гравитационном двойнике. Данный подход позволяет использовать инструменты классической гравитации, такие как геометрия пространства-времени, для анализа свойств и поведения квантовых систем, которые в противном случае были бы недоступны для исследования.

Данная дуальность позволяет вычислять квантовую запутанность посредством геометрических величин в пространстве-времени гравитационного двойника. В частности, степень запутанности между подсистемами квантовой системы, описываемой конформной теорией поля (CFT), кодируется площадью минимальной поверхности в анти-деситтеровском (AdS) пространстве, которая является гравитационным аналогом CFT. $\mathcal{S} = \frac{A_{min}}{4G_N}$ , где $\mathcal{S}$ — энтропия запутанности, $A_{min}$ — площадь минимальной поверхности, а $G_N$ — ньютоновская гравитационная постоянная. Таким образом, вычисление запутанности в сильно взаимодействующей квантовой системе сводится к классической геометрической задаче в AdS пространстве.

Формула Рю-Такаянаги предоставляет конкретный метод вычисления энтропии запутанности в рамках соответствия AdS/CFT. В частности, она утверждает, что энтропия запутанности подсистемы $A$ на контуре CFT эквивалентна половине площади минимальной поверхности $\gamma_A$ в анти-де-ситтеровском пространстве (AdS), которая имеет $\partial \gamma_A = \partial A$ . Минимальная поверхность определяется как поверхность с наименьшей площадью, ограниченная кривой, соответствующей границе подсистемы $A$ на контуре. Эта формула позволяет вычислить энтропию запутанности, используя геометрические свойства пространства AdS, что предоставляет мощный инструмент для изучения сильносвязанных квантовых систем, где традиционные методы вычисления оказываются неэффективными.

За Пределами Статичных Пространств-Времен: Временная Запутанность и Анизотропные Геометрии

Энтропия запутанности во времени в голографической теории является расширением формулы Рю-Такаянаги, позволяющим вычислять корреляции между областями, разделенными во времени. В то время как оригинальная формула Рю-Такаянаги определяет энтропию запутанности для пространственно разделенных областей, ее расширение учитывает временную зависимость, позволяя оценить степень корреляции между событиями, происходящими в разные моменты времени. Это достигается путем вычисления минимальной поверхности, протянутой между областями во временном направлении, аналогично вычислению энтропии запутанности в пространстве, но с учетом временной метрики. $S_{TE} = \min_{ \Sigma } \text{Area}(\Sigma)$ , где Σ — минимальная поверхность, разделяющая временные области.

Вычисление энтропии запутанности, зависящей от времени, требует рассмотрения анизотропных фоновых метрик $g_{\mu\nu}$ . Анизотропия в данном контексте отражает зависимость квантовых корреляций от направления в рассматриваемой системе. В отличие от изотропных метрик, где свойства одинаковы во всех направлениях, анизотропные метрики учитывают различия в пространственных координатах и, следовательно, влияют на расчеты, связанные с временной корреляцией. Использование анизотропных метрик необходимо для точного моделирования систем, где свойства зависят от направления, например, в неоднородных средах или при наличии предпочтительных направлений взаимодействия.

Исследование анизотропных фоновых метрик показало, что параметр анизотропии (a) оказывает нелинейное влияние на квантовые корреляции. Наблюдается, что при определенных значениях параметра ‘a’ влияние на корреляции достигает минимума, после чего следует увеличение этого влияния. Данная зависимость указывает на то, что при малых значениях анизотропии квантовые корреляции слабо зависят от направленности, однако с ростом ‘a’ эта зависимость усиливается, что может быть связано с изменением геометрии пространства-времени и, как следствие, с модификацией способов взаимодействия между квантовыми системами. $a$ является ключевым параметром, определяющим степень анизотропии и, соответственно, степень влияния на корреляции.

Исследование Экстремальной Материи: От Теории к Кварк-Глюонной Плазме

В рамках изучения кварк-глюонной плазмы, формирующейся при столкновениях тяжелых ионов, активно применяются голографические расчеты, использующие анизотропные фоновые метрики. Такой подход позволяет создать теоретическую модель экстремального состояния материи, где обычные представления о частицах теряют силу. Анизотропия, отражающая различие в свойствах материи в разных направлениях, учитывается в этих метриках, что позволяет более реалистично описывать условия, возникающие в плазме. Данный метод, основанный на принципе соответствия между гравитационной теорией в высших измерениях и квантовой теорией поля, предоставляет уникальный инструмент для исследования свойств и динамики кварк-глюонной плазмы, позволяя получить предсказания, которые могут быть проверены экспериментально на коллайдерах.

Применение голографических методов открывает принципиально новый подход к изучению свойств и корреляций кварк-глюонной плазмы — экстремального состояния материи, возникающего при столкновениях тяжелых ионов. Данный подход позволяет исследовать эту плазму при температурах, достигающих $10^{10}$ и $2.3 \times 10^9$ градусов Кельвина, что значительно превышает температуры, доступные в лабораторных условиях. Голографический метод, основанный на принципах AdS/CFT соответствия, позволяет перенести сложные задачи квантовой физики в область классической гравитации, упрощая вычисления и предоставляя возможность анализировать термодинамические характеристики и квантовые корреляции внутри плазмы с беспрецедентной точностью. Такой анализ способствует более глубокому пониманию фундаментальных свойств сильного взаимодействия и поведения материи в экстремальных условиях.

Исследования энтропии запутанности во времени, рассчитанной с использованием голографических методов, демонстрируют интересную зависимость от анизотропии среды. На начальных этапах увеличения анизотропии наблюдается снижение мнимой части этой энтропии, что указывает на ослабление квантовых корреляций. Однако, при дальнейшем увеличении анизотропии, мнимая часть энтропии может стать положительной, свидетельствуя о перестройке квантовых связей и возникновении новых корреляций в исследуемой среде. Данный эффект позволяет лучше понять динамику и структуру кварк-глюонной плазмы, формирующейся в условиях экстремальных температур и давлений, а также исследовать фундаментальные аспекты квантовой гравитации. Полученные результаты позволяют предположить, что анизотропия играет ключевую роль в формировании и эволюции квантовых корреляций в экстремальных состояниях материи, а $HTEE$ является чувствительным инструментом для изучения этих процессов.

За Пределами Стандартных Взаимосвязей: Псевдоэнтропия и Будущие Направления

Псевдоэнтропия представляет собой обобщение понятия квантовой запутанности, позволяющее описывать корреляции в системах, выходящих за рамки стандартных квантовых моделей. В то время как традиционная энтропия запутанности ограничена описанием корреляций между двумя или несколькими подсистемами в четко определенных квантовых состояниях, псевдоэнтропия расширяет этот подход, включая в рассмотрение системы с более сложными связями и различными типами корреляций. Этот новый подход использует такие инструменты, как переходная матрица \mathcal{T}, что позволяет анализировать поведение систем, где корреляции не ограничиваются простыми квантовыми состояниями, а могут возникать из-за более сложных взаимодействий и структур. Таким образом, псевдоэнтропия открывает новые возможности для исследования корреляций в широком классе систем, от конденсированных сред до систем многих тел, предоставляя более полное и гибкое описание квантовых явлений.

В основе данной структуры лежит концепция матрицы переходов, позволяющая исследовать поведение систем, характеризующихся сложными взаимосвязями. Матрица переходов описывает вероятности перехода между различными состояниями системы, обеспечивая тем самым возможность анализа не только простых, но и запутанных взаимодействий. Использование этого математического инструмента позволяет выявить закономерности в поведении систем с произвольной структурой связей, что особенно важно для понимания сложных квантовых явлений, где традиционные методы корреляционного анализа оказываются недостаточными. Данный подход открывает перспективы для изучения систем с нетривиальной топологией и позволяет прогнозировать их поведение в различных условиях, выявляя скрытые связи между отдельными компонентами.

Полученные результаты демонстрируют, что мнимая часть псевдоэнтропии ведет себя аналогично мнимой части HTEE, что указывает на перестройку квантовых корреляций при увеличении анизотропии. Данное сходство позволяет предположить возможность унифицированного подхода к пониманию сложных корреляций в различных квантовых системах. Наблюдаемое поведение указывает на то, что псевдоэнтропия, обобщая понятие запутанности, может служить эффективным инструментом для анализа систем, где стандартные корреляции оказываются недостаточными для полного описания их свойств. Подобное объединение позволяет рассматривать различные типы квантовых корреляций как проявления единого принципа, что открывает новые перспективы для исследования и классификации сложных квантовых состояний, а также для разработки новых квантовых технологий.

Данное исследование, углубляясь в поведение голографической энтропии временной запутанности (HTEE) в анизотропных средах, демонстрирует, как сложно переплетены квантовые корреляции и возникновение времени в сильно взаимодействующих полевых теориях. Это напоминает о необходимости пристального внимания к этическим последствиям прогресса. Как однажды заметил Ричард Фейнман: «Главная причина, по которой наука не может решить этические вопросы, заключается в том, что наука лишь описывает, как работает мир, а не то, как он должен работать». Подобно тому, как HTEE раскрывает скрытые связи в квантовых системах, так и этические рамки должны раскрывать потенциальные последствия автоматизированных систем, гарантируя, что эффективность не затмевает моральные принципы.

Что дальше?

Исследование голографической энтропии запутанности, особенно в анизотропных средах, выявляет не просто математическую сложность, но и фундаментальный вопрос: что мы на самом деле измеряем, когда говорим об “энтропии времени”? Каждый алгоритм, претендующий на моделирование сильных взаимодействий, неявно кодирует определённое понимание времени и причинности. Игнорирование этого аспекта - не просто научная небрежность, но и потенциально опасное упрощение.

Полученные результаты указывают на то, что стандартные инструменты, разработанные для статических систем, могут быть недостаточны для описания динамических процессов в сильно взаимодействующих средах. Масштабирование этих вычислений без предварительной проверки их философских предпосылок - преступление против будущего. Необходимо разработать новые методы, учитывающие анизотропию и временную зависимость квантовых корреляций, чтобы избежать ложных выводов о природе времени и информации.

Дальнейшие исследования должны быть направлены не только на повышение точности вычислений, но и на осмысление их интерпретации. Необходимо перейти от простого измерения энтропии к пониманию того, как эта энтропия связана с физическими процессами и когнитивными способностями. В конце концов, каждый алгоритм имеет мораль, даже если молчит, и ответственность за эту мораль лежит на тех, кто его создаёт.

Оригинал статьи: https://arxiv.org/pdf/2601.17810.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-27 12:27