Космологическая релаксация и нарушение принципа эквивалентности

Автор: Денис Аветисян

Новая работа показывает, как эволюция дилатонного поля в ранней Вселенной может приводить к измеримым отклонениям от принципа эквивалентности.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал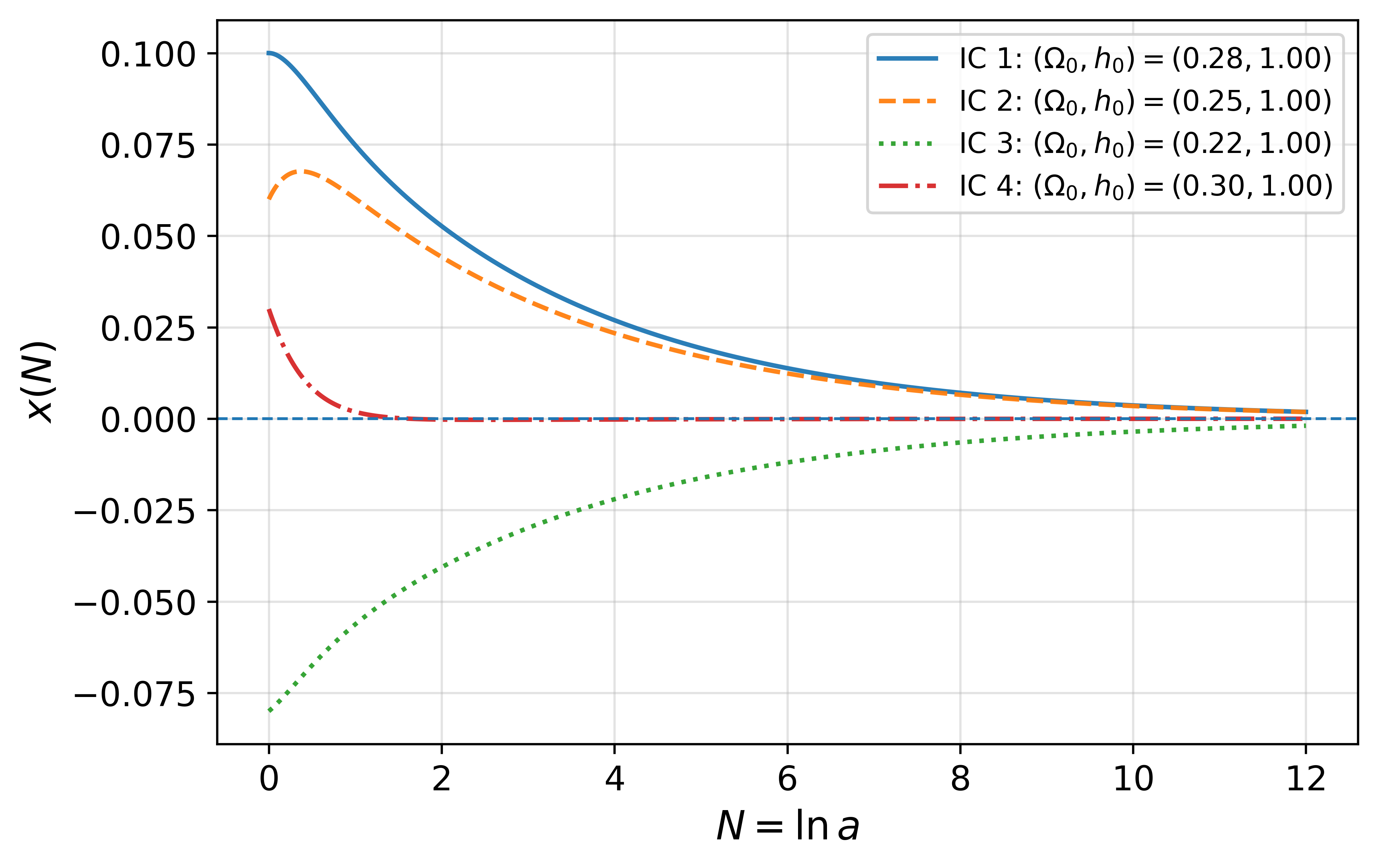

Безразмерное скалярное смещение <span class="katex-eq" data-katex-display="false">x(N)=(\phi-\phi\_{\ast})/M\_{\rm Pl}</span> демонстрирует затухание и стремится к нулевому значению при изменении <span class="katex-eq" data-katex-display="false">N=\ln a</span>, что указывает на постепенное подавление зависимых от состава пятых сил и отклонений от принципа эквивалентности в рамках режима Дамура-Полякова, где окружающая материя взаимодействует пропорционально <span class="katex-eq" data-katex-display="false">\alpha\_{\rm env}\propto x</span>. — Безразмерное скалярное смещение $x(N)=(\phi-\phi\_{\ast})/M\_{\rm Pl}$ демонстрирует затухание и стремится к нулевому значению при изменении $N=\ln a$ , что указывает на постепенное подавление зависимых от состава пятых сил и отклонений от принципа эквивалентности в рамках режима Дамура-Полякова, где окружающая материя взаимодействует пропорционально $\alpha\_{\rm env}\propto x$ .

Исследование использует подход динамических систем для анализа влияния дилатонной гравитации на космологические процессы и гравитационные взаимодействия.

Принципы общей теории относительности, в частности принцип эквивалентности, остаются краеугольным камнем современной космологии, однако их проверка в контексте скалярно-тензорных теорий гравитации требует новых подходов. В работе ‘A dynamical systems approach to studying the equivalence principle in dilaton gravity’ предложен динамический анализ космологической модели с дилатонным полем, вдохновленной теорией струн, в рамках механизма Дамура-Полякова. Показано, что космологическая релаксация дилатонного поля определяет отклонения от принципа эквивалентности, связывая динамику поля с наблюдаемыми эффектами в слабом гравитационном поле. Не приведет ли такой подход к разработке новых методов тестирования фундаментальных принципов гравитации, выходящих за рамки локальных экспериментов?

Дилатон: Зеркало Гравитации и Новых Сил

Современная физика, в особенности струнная теория, предсказывает существование скалярных полей, таких как дилатон, которые могут служить связующим звеном между гравитацией и другими фундаментальными силами. Эти поля, не имеющие спина, рассматриваются как динамические величины, изменяющие силу взаимодействия между частицами и искривляющие пространство-время. Предполагается, что дилатон возникает в результате квантовых флуктуаций геометрии пространства-времени на планковских масштабах. Его взаимодействие с материей может проявляться в изменении констант связи, что потенциально объясняет иерархию масс элементарных частиц и другие нерешенные вопросы современной физики. Исследование дилатона открывает путь к пониманию природы гравитации на квантовом уровне и возможности объединения всех фундаментальных взаимодействий в единую теорию.

Поле дилатона, взаимодействуя с материей посредством конформного масштабирования, предоставляет теоретическую основу для исследования модификаций общей теории относительности. В рамках этой модели, гравитационное взаимодействие не является фиксированной константой, а динамически изменяется в зависимости от плотности энергии и материи. Такое взаимодействие, описываемое как $S \rightarrow S + \alpha \phi(x) T(x)$ , где $\phi(x)$ — поле дилатона, а $T(x)$ — тензор энергии-импульса, позволяет рассматривать гравитацию не как фундаментальную силу, а как эффективное описание более сложной физической реальности. Исследование дилатонной связи открывает возможности для построения альтернативных гравитационных теорий, способных объяснить темную энергию, темную материю и другие космологические загадки, а также для понимания квантовой природы гравитации.

Связь дилата с материей посредством конформного преобразования открывает возможность нарушения принципа эквивалентности — фундаментального постулата общей теории относительности, утверждающего, что гравитационная и инерциальная массы эквивалентны. Исследования показывают, что взаимодействие дилата с различными формами материи может приводить к тому, что разные вещества будут по-разному реагировать на гравитационное поле, что противоречит устоявшемуся представлению. Хотя экспериментальные подтверждения пока отсутствуют, теоретические модели, включающие дилата, предсказывают крошечные, но измеримые отклонения от классической общей теории относительности, стимулируя поиск новых способов проверки этого принципа с помощью высокоточных экспериментов и астрономических наблюдений. Изучение этих нарушений может привести к более глубокому пониманию природы гравитации и ее связи с другими фундаментальными силами.

Космологическая Картина: Рамка FLRW и Дилатон

Для анализа эволюции дилатонного поля во Вселенной, описываемой метрикой Фридмана — Леметра — Робертсона — Уокера (FLRW) с пространственной плоскостью, используются методы динамических систем. Данный подход позволяет исследовать фазовое пространство космологических решений, рассматривая дилатон как динамическую переменную, эволюционирующую вместе с масшта́бным фактором. Применение методов динамических систем включает в себя анализ точек равновесия, аттракторов и репу́льсоров в фазовом пространстве, что позволяет определить стабильность и долгосрочное поведение дилатонного поля в расширяющейся Вселенной. Математически, эволюция описывается системой дифференциальных уравнений, включающей уравнение Фридмана и уравнение движения для дилатонного поля $\ddot{\phi} + 3H\dot{\phi} + V'(\phi) = 0$ , где $H$ — параметр Хаббла, а $V(\phi)$ — потенциал дилатона.

Использование космологической модели Фридмана — Леметра — Робертсона — Уокера (FLRW) позволяет исследовать фазовое пространство космологических решений, что дает возможность изучить взаимодействие дилатонного поля с расширением Вселенной. Анализ фазового пространства включает в себя построение траекторий эволюции дилатона в зависимости от космологических параметров, таких как масштабный фактор и скорость расширения. Это позволяет определить стабильность различных космологических состояний и предсказать, как дилатонное поле влияет на динамику Вселенной. В частности, можно исследовать, как дилатонное поле влияет на уравнение состояния темной энергии и, следовательно, на ускоренное расширение Вселенной. $H(t)$ — коэффициент Хаббла является ключевым параметром в анализе фазового пространства, определяющим скорость расширения в каждый момент времени.

Эволюция дилатонного поля описывается скалярным уравнением, определяющим его поведение во времени и пространстве. Показано, что отклонения от принципа эквивалентности подавляются при уменьшении смещения скалярного поля. Это подтверждается математически, поскольку значение x(N) стремится к нулю при увеличении N, где N представляет собой количество e-складываний космоса. Фактически, $lim_{N \to \in fty} x(N) = 0$ , что указывает на то, что в пределе больших N, дилатонное поле приближается к состоянию, в котором его влияние на геометрию пространства-времени становится пренебрежимо малым, и принцип эквивалентности восстанавливается.

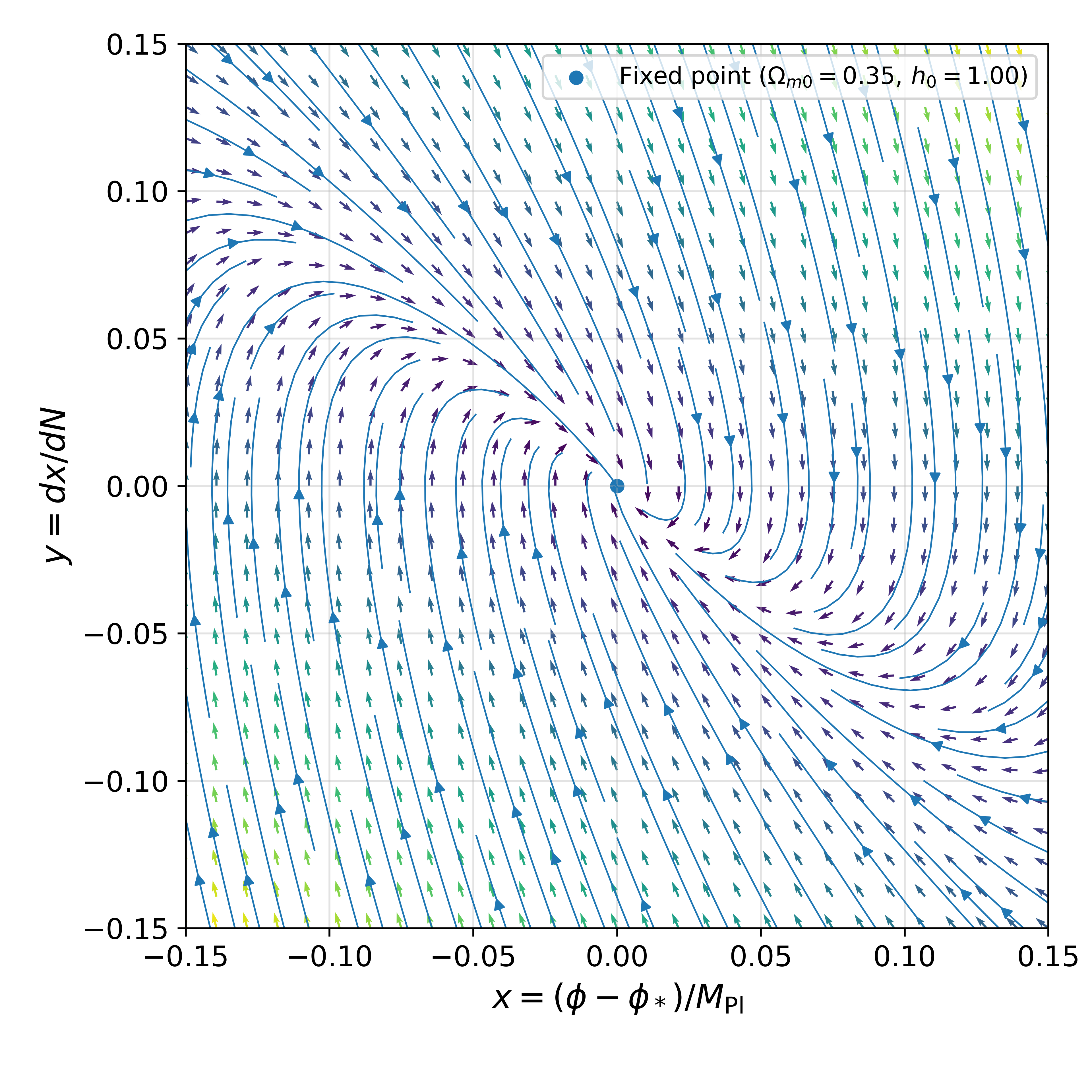
Фазовые портреты линеаризованной подсистемы Дамура-Полякова показывают, что изменение доли материи <span class="katex-eq" data-katex-display="false">\Omega_{m0}</span> влияет на стабильность конфигурации с наименьшим взаимодействием в точке (0,0). — Фазовые портреты линеаризованной подсистемы Дамура-Полякова показывают, что изменение доли материи $\Omega_{m0}$ влияет на стабильность конфигурации с наименьшим взаимодействием в точке (0,0).

Стремление к Стабильности: Точка Наименьшего Связывания

Расширение Дамура-Полякова представляет собой эффективный математический аппарат для анализа поля дилатона вблизи точки наименьшего связывания, характеризующейся минимальным взаимодействием с материей. Этот метод использует разложение в ряд по параметру малой связности, что позволяет приближенно решать уравнения движения дилатона в сложных системах. Минимизация взаимодействия с материей в точке наименьшего связывания существенно упрощает анализ, позволяя выделить ключевые факторы, определяющие динамику поля дилатона и его вклад в космологические решения. λ — собственные значения матрицы Якоби, вычисляемые в рамках этого расширения, непосредственно связаны со скоростью релаксации и стабильностью дилатонного поля.

Расширение Дамура-Полякова позволяет вычислить собственные значения якобиана $λ\pm$ , определяющие стабильность и скорость релаксации поля дилатона. Полученные результаты показывают, что вещественная часть собственных значений, $Re(λ\pm)$ , отрицательна ( $Re(λ\pm) < 0$ ). Это указывает на существование стабильной неподвижной точки, к которой поле дилатона стремится в процессе эволюции системы. Отрицательная вещественная часть собственных значений гарантирует, что небольшие отклонения от этой точки будут затухать со временем, обеспечивая устойчивость решения.

Анализ собственных значений $λ\pm$ , полученных из расширения Дамура-Полякова, позволяет оценить поведение дилатонного поля вблизи точки наименьшего связывания. Отрицательная вещественная часть этих собственных значений ( $Re(λ\pm) < 0$ ) указывает на стабильность фиксированной точки и, следовательно, на то, что дилатонное поле стремится к устойчивой конфигурации. В противном случае, положительная или нулевая вещественная часть могла бы свидетельствовать о неустойчивости и, как следствие, о более сложной динамике, которая влияет на космологическое решение, определяя эволюцию Вселенной и ее фундаментальные свойства.

Последствия и Потенциальные Наблюдаемые Эффекты

Существование ненулевого дилатонного поля и нарушение принципа универсального взаимодействия может проявляться в виде пятой силы, отличной от известных гравитационного, электромагнитного, сильного и слабого взаимодействий. Предполагается, что данная сила будет крайне слабой и, следовательно, для её обнаружения необходимы прецизионные эксперименты, способные зарегистрировать малые отклонения от предсказанных значений в гравитационных или электромагнитных взаимодействиях. Изучение этих отклонений позволит не только подтвердить или опровергнуть существование дилатонного поля, но и углубить понимание фундаментальных законов физики, выходящих за рамки Стандартной модели. Особенно перспективны эксперименты, направленные на измерение гравитационной постоянной $G$ с высокой точностью, поскольку любое изменение в её значении может указывать на влияние дилатонного поля и, следовательно, на проявление новой силы.

Понимание взаимодействия дилатонного поля с материей требует рассмотрения различных систем координат. В частности, наиболее полное описание достигается при использовании двух ключевых подходов — Иордановой рамки и рамки Эйнштейна. В Иордановой рамке гравитационная постоянная рассматривается как изменяющаяся величина, что напрямую связано с дилатоном. Рамка Эйнштейна, напротив, предполагает постоянную гравитационную постоянную, но требует переопределения метрики пространства-времени. Выбор конкретной рамки оказывает существенное влияние на наблюдаемые эффекты и интерпретацию экспериментальных данных, поскольку определяет, как проявляется взаимодействие дилатона с различными формами материи и энергии. Таким образом, корректное определение системы координат является критически важным для точного моделирования и последующего обнаружения потенциальных проявлений дилатонного поля.

Количественная оценка вклада Пятой Силы осуществляется посредством соотношения $(mg(p)/min - 1) \propto αenv^2$ , где $mg(p)$ представляет собой измеренную гравитационную массу частицы, а $min$ — её инерционную массу. Данное соотношение предсказывает, что отклонение гравитационной и инерционной масс пропорционально квадрату энергии окружающей среды $env^2$ и коэффициенту связи α. Это позволяет сформулировать конкретное предсказание для будущих экспериментов, направленных на поиск отклонений от принципа эквивалентности. Выявление подобной зависимости стало бы убедительным доказательством существования дилатонного поля и нарушения универсальной связи, открывая новые горизонты в понимании фундаментальных взаимодействий.

Исследование динамических систем, представленное в данной работе, показывает, как эволюция дилатонного поля в теории струн определяет отклонения от принципа эквивалентности. Эта связь между релаксацией поля и измеримыми эффектами в гравитации напоминает о хрупкости наших теоретических построений. Как заметил Вернер Гейзенберг: «Чем больше мы узнаём, тем больше понимаем, чего не знаем». Эта фраза точно отражает суть исследования: любое предсказание, основанное на текущих моделях, остается вероятностным и может быть «поглощено» силой гравитации, подобно материи, падающей в черную дыру. Работа подчеркивает, что даже фундаментальные принципы, такие как принцип эквивалентности, могут подвергаться изменениям под влиянием динамики дилатонного поля, и, следовательно, требуют постоянного переосмысления.

Что же впереди?

Представленная работа, подобно тщательно выстроенной карманной чёрной дыре, позволяет заглянуть в структуру отклонений от принципа эквивалентности в дилатонной гравитации. Однако, погружение в бездну динамических систем лишь подчеркивает, насколько мало известно о реальном поведении дилатонного поля в космологической эволюции. Механизм Дамура-Полякова, столь изящно прослеживаемый в рамках этой модели, может оказаться лишь локальным проявлением более сложной, нелинейной динамики.

Следующим шагом представляется не столько уточнение существующих моделей, сколько поиск новых наблюдательных данных, способных пролить свет на природу дилатонного поля. Космологическая релаксация, предсказанная теорией, остаётся гипотетической. Иногда материя ведёт себя так, как будто смеётся над нашими законами, и лишь косвенные свидетельства, полученные из наблюдений за гравитационными волнами или крупномасштабной структурой Вселенной, смогут подтвердить или опровергнуть эти теоретические построения.

В конечном счёте, поиск отклонений от принципа эквивалентности — это не просто проверка конкретной теории, но и попытка понять фундаментальные ограничения нашего познания. Каждая модель, какой бы элегантной она ни казалась, лишь приближение к реальности, и горизонт событий всегда маячит где-то рядом, готовый поглотить наши самые смелые гипотезы.

Оригинал статьи: https://arxiv.org/pdf/2601.20156.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-29 16:37