Волны материи в ловушке: новые горизонты динамики

Автор: Денис Аветисян

Физики впервые экспериментально реализовали сверхсильное управление материей в оптическом резонаторе, открывая путь к изучению экзотических явлений, подобных горизонту событий.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

В исследовании демонстрируется, что дискретное преобразование Флоке <span class="katex-eq" data-katex-display="false">f(x)</span> для резонатора, возбуждаемого на основной и второй гармониках, проявляет устойчивые (<span class="katex-eq" data-katex-display="false">f^{\prime}(x)<1</span>) и неустойчивые (<span class="katex-eq" data-katex-display="false">f^{\prime}(x)>1</span>) фиксированные точки на пересечении с <span class="katex-eq" data-katex-display="false">f(x)=x</span>, что находит аналогию в приближённо линейной дисперсии материи в оптической решётке и моделируется захваченными атомами между отталкивающими световыми листами, демонстрируя, как внешнее воздействие может индуцировать появление устойчивой траектории фиксированной точки в изначально диффузном атомном распределении. — В исследовании демонстрируется, что дискретное преобразование Флоке $f(x)$ для резонатора, возбуждаемого на основной и второй гармониках, проявляет устойчивые ( $f^{\prime}(x)<1$ ) и неустойчивые ( $f^{\prime}(x)>1$ ) фиксированные точки на пересечении с $f(x)=x$ , что находит аналогию в приближённо линейной дисперсии материи в оптической решётке и моделируется захваченными атомами между отталкивающими световыми листами, демонстрируя, как внешнее воздействие может индуцировать появление устойчивой траектории фиксированной точки в изначально диффузном атомном распределении.

Экспериментальная реализация резонатора Фабри-Перо для материйных волн в режиме сверхсильного воздействия, демонстрирующая стабильные траектории, предсказанные теорией на основе флокет-отображений и стробоскопической динамики.

Долгое время прямое экспериментальное подтверждение предсказаний теории о концентрации энергии и формировании аналогов горизонтов событий в динамических оптических резонаторах оставалось сложной задачей из-за необходимости релятивистских скоростей для зеркал. В данной работе, посвященной исследованию ‘A matter-wave Fabry-Pérot cavity in the ultrastrong driving regime’, демонстрируется экспериментальная реализация этого принципа, но уже в системе, где роль света и материи взаимозаменяется. Наблюдается формирование устойчивых траекторий, соответствующих предсказанным «ярким» и «темным» фиксированным точкам, а также возможность управления их стабильностью посредством изменения формы модуляции. Какие новые возможности для реализации и изучения аналоговых гравитационных явлений открывает использование материевых волн в динамических резонаторах?

Квантовые полости: Зеркало материи в мире волн

Традиционные оптические резонаторы, основанные на манипулировании фотонами, сталкиваются с фундаментальными ограничениями при работе с материей, представленной в виде волн. В то время как свет эффективно взаимодействует со светом, управление движением атомов и молекул требует принципиально иного подхода. Ограничения связаны с тем, что де-бройлевская длина волны материи, как правило, значительно короче длины волны света, что делает применение стандартных оптических методов неэффективным и сложным. Это порождает необходимость в создании резонаторов, способных эффективно удерживать и контролировать именно материю, открывая путь к новым исследованиям в области квантовой оптики и разработке инновационных технологий, использующих уникальные свойства материи на квантовом уровне.

Разработка волновых полостей для материи, использующих атомы в качестве “света”, открывает принципиально новую область для исследования квантовых явлений. В отличие от традиционных оптических резонаторов, манипулирующих фотонами, эти полости позволяют контролировать движение атомов с беспрецедентной точностью. Такой подход позволяет создавать условия, в которых атомы ведут себя как волны, интерферируя и образуя стоячие волны материи. Это, в свою очередь, создает уникальные возможности для изучения фундаментальных аспектов квантовой механики, таких как суперпозиция и запутанность, а также для разработки новых квантовых технологий, включая сверхчувствительные датчики и квантовые вычислительные устройства. Исследования в этой области позволяют исследовать границы между классической и квантовой физикой и открывают перспективы для создания принципиально новых материалов с необычными свойствами.

Атомные полости представляют собой принципиально новый подход к управлению движением атомов, открывая перспективы для создания инновационных квантовых технологий. В отличие от традиционных оптических резонаторов, использующих фотоны, эти полости используют сами атомы как «свет», обеспечивая беспрецедентный уровень контроля над их траекториями и взаимодействиями. Точное манипулирование атомным движением позволяет создавать квантовые системы с заданными свойствами, что необходимо для разработки высокоточных сенсоров, квантовых вычислительных устройств и совершенно новых методов квантовой связи. Благодаря возможности локализации и удержания атомов в строго определенных областях пространства, эти полости представляют собой платформу для исследования фундаментальных квантовых явлений и реализации сложных квантовых алгоритмов, способных превзойти возможности классических компьютеров. Перспективные исследования направлены на создание масштабируемых атомных полостей, что позволит значительно увеличить количество контролируемых атомов и, следовательно, сложность решаемых задач.

Атомы Бозе-Эйнштейна адиабатически загружаются в оптическую решетку за 200 мс при отключении перекрестной дипольной ловушки, после чего резонансная амплитудная модуляция решетки и градиент магнитного поля переводят атомы из S-зоны в D-зону, придавая им квазирелятивистскую дисперсию, а удержание волны материи осуществляется сине-детунированными световыми листами, создаваемыми акустооптическим дефлектором, с последующим снижением силы и синусоидальной модуляцией частот дефлектора для создания необходимой модуляции границы нижней стенки с фазой φ.

Динамические решетки и зависимое от времени уравнение Шрёдингера

Для создания динамических оптических решеток, формирующих границы оптического кавака, используются акустооптические дефлекторы. Эти устройства изменяют направление и интенсивность света, модулируя потенциал, в котором удерживаются атомы. Применяется принцип дифракции света на ультразвуковых волнах, генерируемых дефлектором, что позволяет создавать пространственно-временные изменения оптического потенциала. Регулируя частоту и амплитуду ультразвуковых волн, можно контролировать параметры решетки, такие как глубина потенциальной ямы и период решетки, обеспечивая тем самым динамическое управление атомами внутри кавака. Такой подход позволяет создавать искусственные потенциальные ландшафты для исследования квантовых явлений и управления атомными волнами.

Поведение системы, включающей ультрахолодные атомы в динамических оптических решетках, описывается фундаментальным уравнением $i\hbar\frac{\partial}{\partial t}\Psi(\mathbf{r},t) = \hat{H}(t)\Psi(\mathbf{r},t)$ , известным как зависящее от времени уравнение Шрёдингера. Данное уравнение определяет эволюцию во времени волновой функции $\Psi(\mathbf{r},t)$ , полностью характеризующей состояние атомов в пространстве и времени. Оператор $\hat{H}(t)$ представляет собой гамильтониан системы, включающий кинетическую энергию атомов и потенциальную энергию, создаваемую динамической оптической решеткой. Решение этого уравнения позволяет предсказывать и анализировать динамику атомов, включая их перемещение, взаимодействие и возможные квантовые эффекты, возникающие в условиях изменяющегося потенциала.

Модуляция акустооптических дефлекторов позволяет создавать динамические оптические решетки, функционирующие как “движущиеся зеркала” для атомов. Аналогично отражению фотонов в оптических резонаторах, эти решетки формируют изменяющиеся во времени границы потенциальной ямы для атомов, вызывая их отражение и управляя их движением. Экспериментально достигнутые скорости “зеркал” превышают 1% от эффективной скорости света для используемых атомов, что открывает возможности для исследования релятивистских эффектов в контексте атомной физики и квантовых симуляций. Эффективная скорость света в данном контексте определяется параметрами атомной системы и используемой оптической решетки.

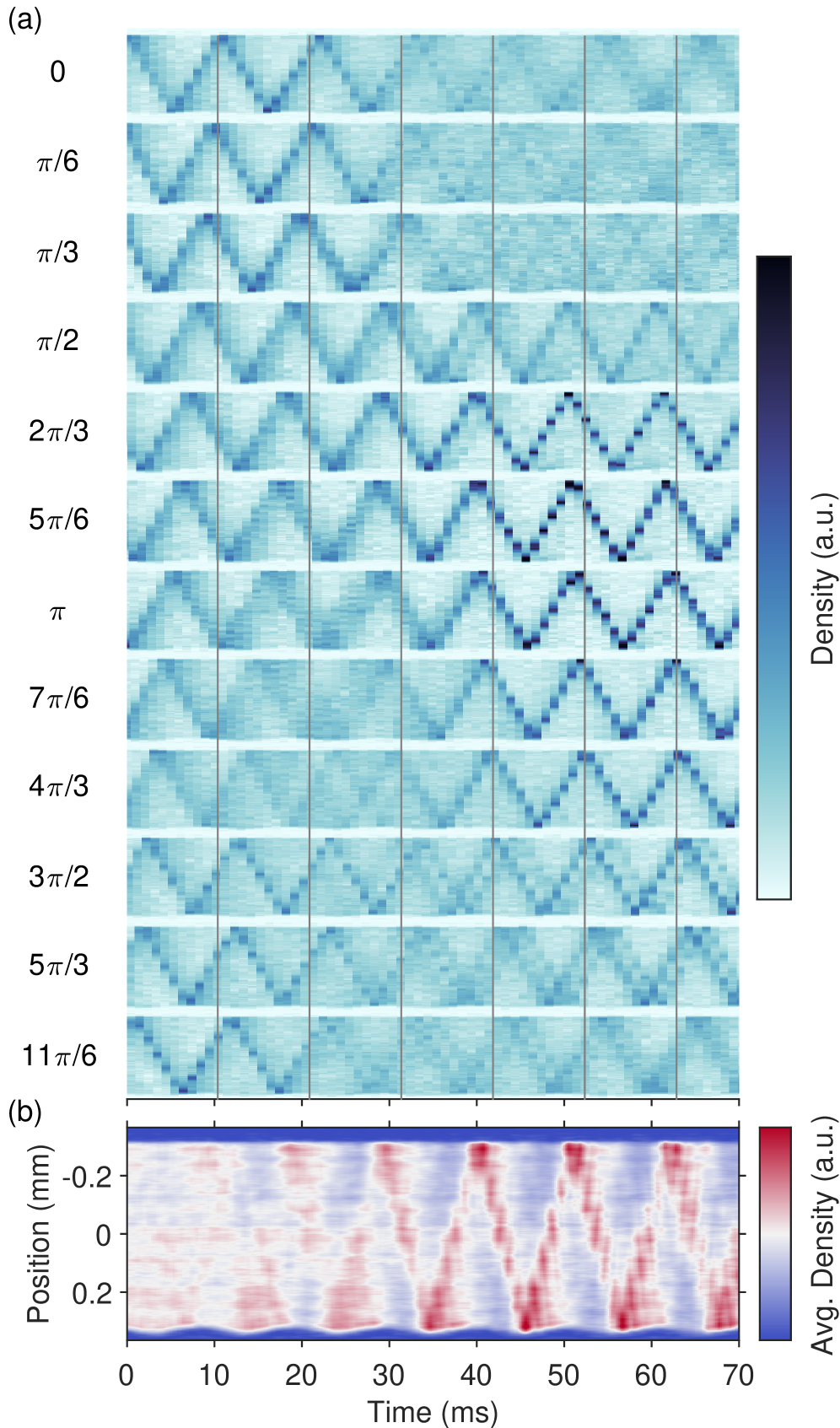
Применение модуляции границы позволило добиться сходимости траекторий атомов, стартующих из различных начальных условий, к стабильной фиксированной точке (красная треугольная волна) и отталкивания от нестабильной (синяя треугольная волна), что демонстрирует эффективное управление динамикой частиц в полости.

Карта Флоке и возникающая динамика

Карта Флоке представляет собой стробоскопический взгляд на эволюцию атомов в периодически изменяющемся потенциале. Она позволяет анализировать динамику системы в дискретные моменты времени, соответствующие периоду изменения потенциала. В результате такого анализа выявляются неподвижные точки, соответствующие стационарным решениям уравнения Шрёдингера в данном потенциале. Стабильность этих неподвижных точек определяет поведение атомных волновых пакетов: стабильные точки соответствуют локализованным состояниям, а нестабильные — экспоненциально растущим или расходящимся решениям. Анализ собственных значений матрицы Якоби в каждой неподвижной точке позволяет определить характер этой стабильности и предсказать дальнейшую эволюцию системы. $\dot{x} = F(x)$ , где $x$ — состояние системы, а $F$ — периодическое возмущение.

Стационарные точки отображения Флоке представляют собой локализованные атомные волновые пакеты, что аналогично резонансным модам в оптических резонаторах. В оптических резонаторах, определенные частоты света усиливаются за счет многократных отражений между зеркалами, формируя устойчивые пространственные распределения электромагнитного поля. Аналогичным образом, в динамической оптике с движущимися зеркалами, стационарные точки соответствуют состояниям, в которых атомные волновые функции сохраняют свою форму и положение после каждого «стробоскопического» наблюдения, определяемого движением зеркал. Эти локализованные волновые пакеты характеризуются определенной энергией и пространственным распределением, которые определяются параметрами системы, включая скорость движения зеркал и дисперсионные свойства атомов. $\omega = v/L$ , где ω — частота, $v$ — скорость движения зеркал, а $L$ — эффективная длина резонатора.

Взаимодействие движущихся зеркал и дисперсионных соотношений для атомов может приводить к появлению неустойчивых неподвижных точек на карте Флоке. Данная неустойчивость обусловлена тем, что изменение параметров системы (скорость зеркал, атомная масса, и т.д.) вызывает экспоненциальный рост решений вблизи этих точек. Математически это выражается в виде собственных значений матрицы Якоби, соответствующих данной точке, имеющих положительную вещественную часть. Этот механизм обеспечивает усиление атомных волновых пакетов, что может быть использовано в различных приложениях, таких как создание когерентных атомных пучков или разработка квантовых усилителей. $\lambda > 0$ является условием экспоненциального роста.

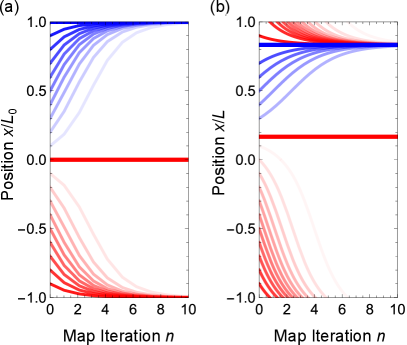
Анализ карт Флоке показывает, что в резонансном случае (<span class="katex-eq" data-katex-display="false">A=L_0/10</span>, <span class="katex-eq" data-katex-display="false">\phi=0</span>) неустойчивая фиксированная точка находится в <span class="katex-eq" data-katex-display="false">x_{unstable}=0</span>, а остальные точки стремятся к стабильной точке <span class="katex-eq" data-katex-display="false">x_{stable}=\pm L_0</span>, тогда как в нерезонансном случае (<span class="katex-eq" data-katex-display="false">A=L/10</span>, <span class="katex-eq" data-katex-display="false">\Delta=L/20</span>) неустойчивая точка смещается в <span class="katex-eq" data-katex-display="false">x_{unstable}=L/6</span>, а устойчивая - в <span class="katex-eq" data-katex-display="false">x_{stable}=5L/6</span>. — Анализ карт Флоке показывает, что в резонансном случае ( $A=L_0/10$ , $\phi=0$ ) неустойчивая фиксированная точка находится в $x_{unstable}=0$ , а остальные точки стремятся к стабильной точке $x_{stable}=\pm L_0$ , тогда как в нерезонансном случае ( $A=L/10$ , $\Delta=L/20$ ) неустойчивая точка смещается в $x_{unstable}=L/6$ , а устойчивая — в $x_{stable}=5L/6$ .

Релятивистская дисперсия и D-полоса

Перевод атомов во второе возбужденное состояние Блоховской полосы (D-полосу) приводит к возникновению релятивистского соотношения дисперсии. В этом уникальном режиме, энергия и импульс атомов связаны линейно, что существенно отличается от классического поведения и обусловлено особенностями зонной структуры кристалла. Такое поведение, аналогичное релятивистской зависимости между энергией и импульсом в физике элементарных частиц, проявляется из-за сильного взаимодействия между атомами и периодическим потенциалом кристаллической решетки. В результате, даже при умеренных скоростях, атомы демонстрируют эффекты, обычно наблюдаемые только при скоростях, близких к скорости света, что открывает новые возможности для управления и манипулирования материей на атомном уровне.

Уникальный режим дисперсии, характеризующийся линейной зависимостью между энергией и импульсом, существенно усиливает неустойчивость системы. В отличие от традиционных дисперсионных соотношений, где энергия обычно изменяется нелинейно с импульсом, данная линейная связь приводит к более быстрому росту возмущений. Это происходит из-за того, что даже небольшое изменение импульса вызывает пропорциональное изменение энергии, что, в свою очередь, усиливает отклонения от равновесного состояния. $E = vk$ , где $E$ — энергия, $v$ — скорость, а $k$ — волновой вектор, является упрощенным представлением данной зависимости. Подобная дисперсия создает условия для экспоненциального роста возмущений, что приводит к более быстрой и интенсивной неустойчивости по сравнению с системами, обладающими нелинейной дисперсией.

Характеристика начального разброса квазиимпульса для блоховских волн во второй возбужденной полосе (D-полосе) была проведена с точностью до 0.1 $\hbar k_L$ . Достижение подобной точности стало возможным благодаря использованию численного моделирования с пространственным разрешением в 5.7 нм. Это позволило детально смоделировать волновой пакет, имеющий размер 106 мкм (FWHM), что критически важно для анализа поведения частиц в условиях релятивистской дисперсии и последующего усиления неустойчивостей. Высокое разрешение моделирования обеспечивает достоверное описание волновой функции и позволяет выявить тонкие эффекты, влияющие на динамику системы.

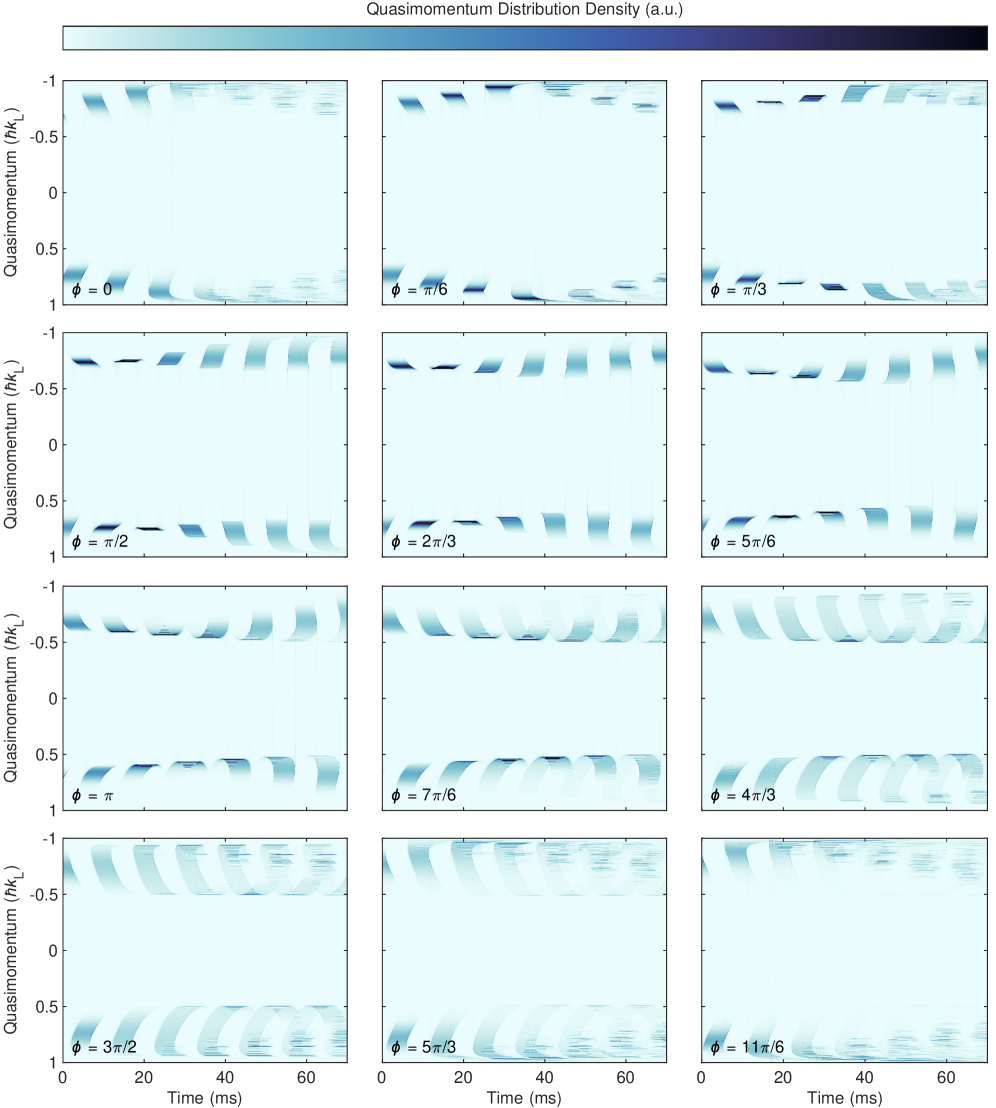
Моделирование эволюции квазиимпульса в полосе DD показывает, что определенные фазы модуляции приводят к перемещению атомов к краю зоны Бриллюэна и, как следствие, к туннелированию Ландау-Зенера в более высокие энергетические уровни.

Будущие направления: Квантовый контроль и за его пределами

Точный контроль над картой Флоке и атомной дисперсией открывает принципиально новые возможности для создания квантовых состояний с заданными характеристиками. Исследователи демонстрируют, что, манипулируя параметрами периодического воздействия на атомы в этих “квантовых полостях”, можно формировать волновые функции, оптимизированные для конкретных задач. $\psi(t) = U(t) \psi(0)$ — эта формула отражает суть управления квантовым состоянием посредством унитарного оператора $U(t)$ , определяемого картой Флоке. Варьируя временные параметры и интенсивность лазерных импульсов, можно не только управлять энергией и импульсом атомов, но и создавать сложные запутанные состояния, необходимые для квантовых вычислений и сенсорики. Такой подход позволяет преодолеть ограничения, связанные со спонтанным распадом квантовых состояний, и значительно увеличить время когерентности, что является ключевым фактором для реализации надежных квантовых технологий.

Исследование хиральных решений в рамках флокэтовского отображения открывает перспективные пути к созданию принципиально новых топологических явлений и, как следствие, высокостабильных квантовых устройств. Хиральность, проявляющаяся в асимметрии поведения квантовых частиц, позволяет формировать состояния, устойчивые к различным возмущениям и дефектам среды. В рамках флокэтовского формализма, описывающего периодически управляемые квантовые системы, возможность целенаправленного формирования хиральных состояний позволяет создавать устройства, в которых информация кодируется и обрабатывается посредством топологически защищенных мод. Это особенно важно для реализации надежных квантовых вычислений и создания квантовых сенсоров, невосприимчивых к шумам и внешним воздействиям. Подобные системы потенциально способны к выполнению сложных квантовых алгоритмов с высокой точностью и эффективностью, представляя собой значительный шаг вперед в области квантовых технологий.

Созданные микроскопические волновые полости с атомами представляют собой исключительно гибкую платформу для целого ряда научных исследований. Данные структуры позволяют проводить квантовое моделирование сложных систем, имитируя поведение квантовых частиц в контролируемой среде, что открывает возможности для разработки новых материалов с заданными свойствами. Более того, эти полости служат уникальным инструментом для фундаментальных исследований в области физики, позволяя изучать явления, связанные с квантовой механикой и взаимодействием света с материей на новом уровне точности. Их адаптивность позволяет настраивать параметры системы для изучения различных физических процессов, делая их ценным активом для материаловедения, квантовой химии и поиска новых физических принципов. $\Psi(x,t)$ — волновой пакет, описывающий поведение частиц в этих полостях, может быть точно контролирован и измерен, что обеспечивает беспрецедентные возможности для научных открытий.

Стробоскопическая относительность проявляется в представлении резонансного отображения Флоке <span class="katex-eq" data-katex-display="false">Eq. (S23)</span> в хиральной кольцевой геометрии, где неустойчивые и устойчивые фиксированные точки соответствуют аналогичным горизонтам событий черных и белых дыр, определяющим однонаправленное распространение света. — Стробоскопическая относительность проявляется в представлении резонансного отображения Флоке $Eq. (S23)$ в хиральной кольцевой геометрии, где неустойчивые и устойчивые фиксированные точки соответствуют аналогичным горизонтам событий черных и белых дыр, определяющим однонаправленное распространение света.

Исследование демонстрирует, как даже самые элегантные теоретические конструкции, такие как карты Флоке и стробоскопическая динамика, сталкиваются с суровой реальностью экспериментов в области ультрасильных воздействий. Подобно чёрной дыре, поглощающей свет, ультрасильно возбужденный волновой кавитатор скрывает предсказуемые траектории, заменяя их стабильными, но не менее загадочными, аналогичными горизонту событий. Юрген Хабермас однажды заметил: «Коммуникативное действие нуждается в рациональной аргументации». Однако, здесь рациональная аргументация сталкивается с необходимостью интерпретировать данные, которые отказываются следовать привычным законам. Физика, как искусство догадок под давлением космоса, вновь напоминает о своей непредсказуемости.

Что дальше?

Представленные результаты, демонстрирующие экспериментальную реализацию фабри-перовской резонаторной системы для материйских волн в режиме ультрасильного возбуждения, открывают новые возможности для исследования аналогов горизонтов событий. Однако, следует признать, что сопоставление наблюдаемых траекторий со строго определенными решениями метрик Шварцшильда и Керра требует осторожности. Любая попытка экстраполировать результаты на квантовую гравитацию сталкивается с необходимостью аккуратной интерпретации операторов наблюдаемых и учета эффектов, выходящих за рамки классического описания.

В дальнейшем, особое внимание следует уделить исследованию динамического эффекта Казимира в предложенной системе. Строгий анализ флокэтовской карты, описывающей эволюцию материйской волны, позволит выявить условия, при которых наблюдаемый эффект максимально близок к теоретическим предсказаниям. При этом, важно помнить, что любая теоретическая модель — лишь приближение к реальности, и её границы определяются горизонтом событий нашего понимания.

Очевидным направлением для дальнейших исследований является расширение параметров системы и исследование более сложных режимов возбуждения. Однако, истинный прогресс потребует не только технических усовершенствований, но и философского осмысления природы наблюдаемых явлений. Ведь чёрная дыра — это не просто объект, это зеркало нашей гордости и заблуждений.

Оригинал статьи: https://arxiv.org/pdf/2601.21122.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-30 16:19