Колебания в критическом одномерном мире: новый взгляд на амплитудные моды

Автор: Денис Аветисян

Исследование раскрывает свойства и механизм возбуждения амплитудных мод в одномерной критической системе, демонстрируя их связь с фундаментальными принципами теории конденсированного состояния.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал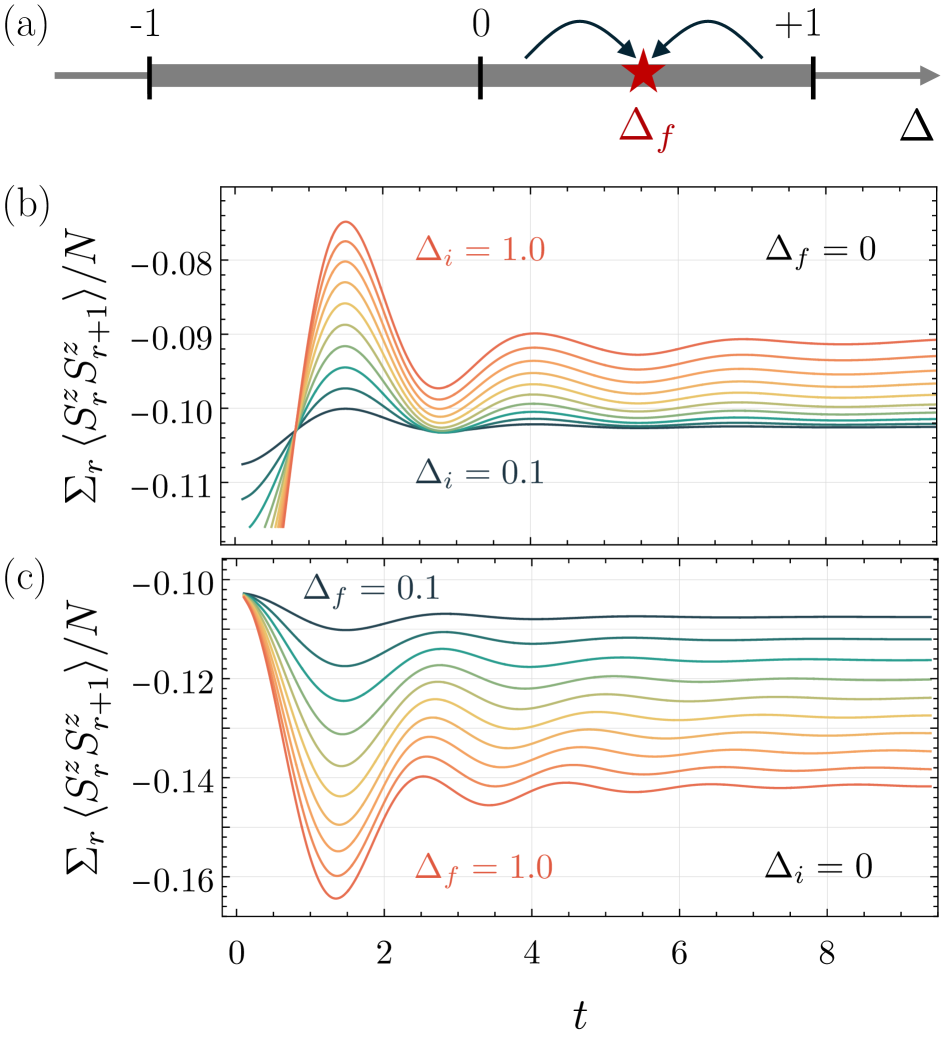

В исследовании динамики квантовой системы, резко переведенной из начального состояния, описываемого гамильтонианом <span class="katex-eq" data-katex-display="false">H(\Delta_i)</span>, в конечное состояние с гамильтонианом <span class="katex-eq" data-katex-display="false">H(\Delta_f)</span>, установлено, что частота колебаний возбуждаемого оператора <span class="katex-eq" data-katex-display="false">\mathcal{O}^{zz}</span> определяется величиной <span class="katex-eq" data-katex-display="false">\Delta_f</span>, а амплитуда - абсолютной разницей между начальным и конечным параметрами <span class="katex-eq" data-katex-display="false">\lvert\Delta_f - \Delta_i\rvert</span>, что демонстрирует закономерную связь между параметрами перехода и динамикой системы. — В исследовании динамики квантовой системы, резко переведенной из начального состояния, описываемого гамильтонианом $H(\Delta_i)$ , в конечное состояние с гамильтонианом $H(\Delta_f)$ , установлено, что частота колебаний возбуждаемого оператора $\mathcal{O}^{zz}$ определяется величиной $\Delta_f$ , а амплитуда — абсолютной разницей между начальным и конечным параметрами $\lvert\Delta_f - \Delta_i\rvert$ , что демонстрирует закономерную связь между параметрами перехода и динамикой системы.

В работе идентифицирована и охарактеризована слабозатухающая амплитудная мода в безщелевой фазе одномерной модели XXZ, возникающая при квантовых сбросах и объясняемая в рамках подхода Бете.

В рамках изучения коллективных возбуждений в квантовых системах часто возникают сложности с выделением и характеристикой мод, не связанных со спонтанным нарушением симметрии. В настоящей работе, посвященной ‘Quench spectroscopy of amplitude modes in a one-dimensional critical phase’, исследуется возникновение амплитудной (подобной хиггсовской) моды в безщелевой фазе одномерной спиновой цепочки XXZ. Показано, что данная мода проявляется как затухающие колебания U(1)-симметричных наблюдаемых после внезапного квенча, а её микроскопическое происхождение связано с определенными семействами стринговых возбуждений в рамках решения Бете. Какие новые возможности для исследования коллективных возбуждений открываются с использованием методов квенч-спектроскопии и программируемых квантовых симуляторов?

За пределами равновесия: Открытие динамики XXZ спиновой цепи

Понимание динамики систем, находящихся вдали от равновесия, имеет первостепенное значение для описания широкого спектра физических явлений. В то время как традиционная термодинамика фокусируется на стабильных состояниях, многие реальные процессы происходят в условиях постоянных возмущений и отклонений от равновесия. Исследование таких систем требует новых теоретических подходов и экспериментальных методов, способных учесть нелинейные эффекты и временную эволюцию. От понимания этих процессов зависит прогресс в материаловедении, физике конденсированного состояния и даже в биологии, где не-равновесные процессы являются основой жизни. Изучение того, как системы реагируют на внезапные изменения, как энергия перераспределяется и как формируются новые структуры, открывает возможности для создания новых технологий и углубления нашего понимания окружающего мира.

Цепь XXZ спинов представляет собой исключительно гибкую модель, позволяющую исследовать широкий спектр квантовых явлений, поскольку она эффективно отражает фундаментальные взаимодействия, возникающие в конденсированных средах. Данная модель описывает систему взаимодействующих спинов, где взаимодействие зависит от направления, что позволяет воспроизводить как ферромагнитное, так и антиферромагнитное упорядочение. $S^x$ , $S^y$ и $S^z$ компоненты спина взаимодействуют между собой, определяя энергетику системы и её динамическое поведение. Благодаря своей относительной простоте и в то же время достаточной сложности, цепь XXZ служит идеальной площадкой для проверки теоретических предсказаний и разработки новых методов анализа квантовых систем, находящихся вдали от равновесия. Её универсальность позволяет адаптировать модель для изучения различных физических задач, включая магнетизм, сверхпроводимость и квантовые вычисления.

Богатая фазовая диаграмма XXZ спиновой цепи, включающая в себя жидкость Латтингера, представляет собой уникальную площадку для проверки и развития теоретических методов в области конденсированного состояния. Эта одномерная модель демонстрирует широкий спектр состояний — от ферромагнитного упорядочения до спиновых жидкостей — в зависимости от параметров взаимодействия. Жидкость Латтингера, характеризующаяся коллективным поведением спинов и отсутствием дальнодействия, служит особенно сложным и интересным объектом для теоретического анализа, требующим применения передовых методов, таких как теория поля Бозонизации и метод Монте-Карло. Исследование фазовых переходов и критических явлений в XXZ цепи позволяет не только углубить понимание фундаментальных свойств квантовых систем, но и разработать новые подходы к решению сложных задач в физике конденсированного состояния и за ее пределами.

Исследование отклика XXZ спиновой цепи на внезапные возмущения, известные как квантовые скачки, позволяет получить ценные сведения о перераспределении энергии в квантовых системах. В подобных экспериментах система, находящаяся в определенном состоянии, мгновенно переводится в новое состояние посредством изменения параметров. Этот процесс запускает сложную динамику, в которой энергия перетекает между различными модами системы, приводя к возникновению новых корреляций и не-равновесных состояний. Анализ этих процессов, включающий в себя изучение временной эволюции корреляционных функций и спектральных свойств, позволяет установить, как энергия распределяется между различными степенями свободы и как система стремится к новому, возможно не-равновесному, состоянию. Данный подход не только углубляет понимание фундаментальных аспектов квантовой динамики, но и открывает перспективы для разработки новых методов управления квантовыми системами и создания когерентных квантовых устройств.

Метод Бете: Точное решение для XXZ спиновой цепи

Метод Бете предоставляет точное аналитическое решение для модели XXZ спиновой цепи, позволяя полностью определить спектр её возбуждений. В отличие от приближенных методов, таких как теория возмущений, метод Бете позволяет получить точные значения энергий всех возможных состояний системы. Это достигается путем построения волновой функции, зависящей от параметров, называемых «быстротами» (rapidities), которые определяют квантовые числа, характеризующие импульс и энергию возбуждений. Точность решения метода Бете подтверждена сравнением с численными методами для различных значений параметров модели XXZ, что делает его важным инструментом для изучения свойств одномерных квантовых систем. $H|Ψ⟩ = E|Ψ⟩$ — уравнение, описывающее точное определение энергии $E$ для каждого возбужденного состояния $|Ψ⟩$ .

В методе Бете “быстрые переменные” (rapidities) являются ключевыми параметрами, полностью определяющими энергию и импульс возбуждений в системе. Каждое возбуждение характеризуется своим набором быстрых переменных, которые являются решениями системы нелинейных интегральных уравнений, известных как уравнения Бете. Эти переменные не являются физическими импульсами в обычном смысле, а скорее математическими конструкциями, позволяющими вычислить спектр энергий и импульсов возможных состояний системы. Значение каждой переменной связано с энергией соответствующего возбуждения, а их комбинации определяют полный энергетический спектр и динамические свойства XXZ спиновой цепи. $\epsilon = \frac{1}{2} \sum_{i=1}^{N} \frac{k_i^2}{k_i + i}$ — пример формулы, где ε — энергия, а $k_i$ — быстрые переменные.

Быстрые параметры (rapidities) в методе Бетhe могут объединяться в “строки” (strings), представляющие собой коллективные возбуждения системы. Каждая строка состоит из последовательности быстрых параметров, и количество параметров в строке определяет число частиц, участвующих в коллективном возбуждении. Эти строки обладают специфическими свойствами, отличными от свойств отдельных возбуждений, и их конфигурация существенно влияет на энергетический спектр и динамику XXZ спиновой цепи. Наличие строк объясняет появление сложных корреляций между спинами и позволяет точно рассчитать энергию и импульс коллективных мод возбуждения, что невозможно при рассмотрении только независимых частиц.

Конфигурация быстрых частиц (rapidities) играет ключевую роль в понимании динамики XXZ-цепи, решаемой методом Бете. В частности, конфигурация «две частицы — две дырки» (two-particle-two-hole configuration) описывает возбуждения, возникающие при добавлении или удалении спина. Дырки представляют собой отсутствие частицы в определенном состоянии, а комбинация двух частиц и двух дырок позволяет описать сложные корреляции и коллективные возбуждения системы. Анализ таких конфигураций позволяет вычислить энергию и импульс возбужденных состояний, а также предсказать поведение системы в различных внешних условиях. Понимание взаимосвязи между конфигурациями быстрых частиц и физическими свойствами системы является центральным аспектом применения метода Бете.

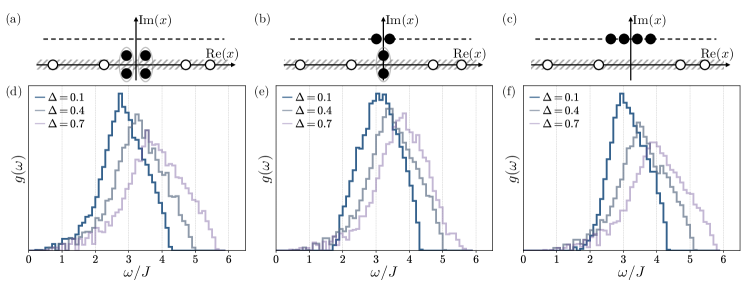
Исследования трех типов возбуждений (I-III), характеризующихся наличием дырок на вещественной оси (открытые кружки) и парных состояний или комплексных быстрот длины 1 (заполненные кружки), показывают, что при малых значениях Δ спектр плотности состояний <span class="katex-eq" data-katex-display="false">g(\omega)</span> для семейства возбуждений типа I плавно переходит в спектр свободных фермионов, с совпадающим пиком и непрерывным расширением до <span class="katex-eq" data-katex-display="false">\omega=0</span>. — Исследования трех типов возбуждений (I-III), характеризующихся наличием дырок на вещественной оси (открытые кружки) и парных состояний или комплексных быстрот длины 1 (заполненные кружки), показывают, что при малых значениях Δ спектр плотности состояний $g(\omega)$ для семейства возбуждений типа I плавно переходит в спектр свободных фермионов, с совпадающим пиком и непрерывным расширением до $\omega=0$ .

Раскрытие коллективных возбуждений и симметрии

Ключевым возбуждением в цепочке XXZ является ‘мода амплитуды’ — коллективная осцилляция спинового порядка. Данная мода представляет собой когерентное движение спинов, отклоняющееся от равновесного состояния, и характеризуется определенной частотой и волновым вектором. В отличие от индивидуальных возбуждений, таких как спиновые волны, мода амплитуды включает в себя скоординированное движение большого числа спинов, что делает её макроскопическим проявлением коллективного поведения системы. Наблюдение данной моды свидетельствует о сильной корреляции между спинами и наличии дальнодействующего порядка в системе.

Коллективное возбуждение, известное как амплитудный мод, тесно связано с U(1) симметрией модели XXZ. Данная симметрия описывает инвариантность системы относительно вращений спинов в двумерном пространстве. Любое изменение спинов, которое соответствует вращению всех спинов на один и тот же угол, не меняет физические свойства системы, что и является проявлением U(1) симметрии. В результате, амплитудный мод представляет собой колебание спинового порядка, которое возможно благодаря сохранению спинового момента и связано с возбуждениями, преобразующимися как скаляры под U(1) группой.

Появление амплитудного мода может быть объяснено анализом плотности состояний $D(E)$ . Особенности в $D(E)$ , такие как сингулярность Ван Хове, указывают на критические энергетические уровни, при которых возникают коллективные возбуждения. Сингулярность Ван Хове соответствует резкому увеличению числа состояний с определенной энергией, что приводит к возникновению амплитудного мода, проявляющегося как колебание спинового порядка. Анализ $D(E)$ позволяет идентифицировать энергию этого мода и его вклад в общее возбужденное состояние системы.

В ходе анализа XXZ-цепи был идентифицирован слабозатухающий амплитудный мод, характеризующийся частотой колебаний приблизительно равной 2.5 $J$ . Данный результат был подтвержден численными расчетами для системы размером N = 100. Наличие слабого затухания указывает на то, что данный мод представляет собой коллективное возбуждение, способное распространяться на значительные расстояния без существенной потери энергии. Полученное значение частоты является ключевым параметром, определяющим динамические свойства спиновой системы.

Интересно, что коллективные возбуждения, аналогичные модам амплитуды в XXZ-цепи, обнаруживаются и в, казалось бы, не связанных моделях, таких как модель Изинга. Несмотря на различную физическую природу и симметрию — в модели Изинга преобладает $ℤ₂$ симметрия, в отличие от U(1) симметрии XXZ-цепи — возникают коллективные колебания спинового порядка. Это указывает на общие принципы, управляющие возникновением подобных возбуждений в системах с различной симметрией и взаимодействиями, и позволяет предположить универсальность данного явления в более широком классе магнитных материалов.

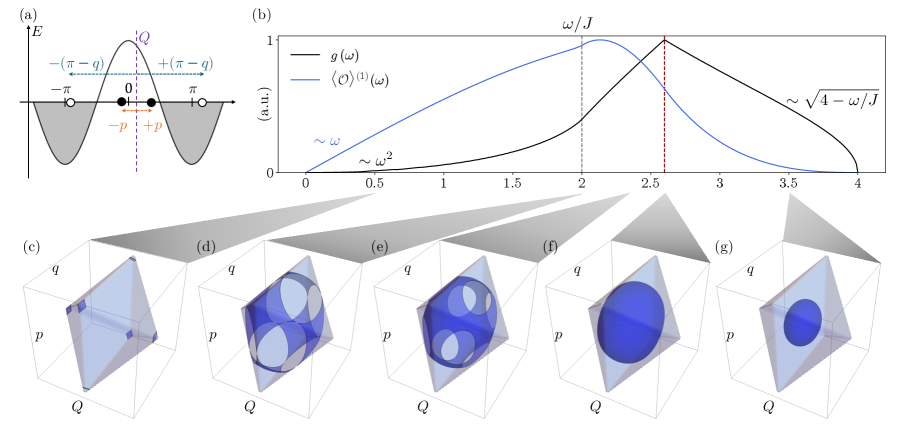
Параметризация четырех кристаллических импульсов позволяет исследовать зависимость плотности состояний <span class="katex-eq" data-katex-display="false">g(\omega)</span> и ее Фурье-компоненты от <span class="katex-eq" data-katex-display="false">\omega/J</span>, демонстрируя, что при определенных значениях параметра <span class="katex-eq" data-katex-display="false">\omega/J</span> (особенно около 2 и <span class="katex-eq" data-katex-display="false">3\sqrt{3}/2</span>), морфология поверхности в пространстве параметров (Q, p, q) изменяется, отражая появление особенностей в плотности состояний и, как следствие, дефектов на поверхности. — Параметризация четырех кристаллических импульсов позволяет исследовать зависимость плотности состояний $g(\omega)$ и ее Фурье-компоненты от $\omega/J$ , демонстрируя, что при определенных значениях параметра $\omega/J$ (особенно около 2 и $3\sqrt{3}/2$ ), морфология поверхности в пространстве параметров (Q, p, q) изменяется, отражая появление особенностей в плотности состояний и, как следствие, дефектов на поверхности.

Влияние на динамику неравновесных систем

Метод Бете, в сочетании с анализом коллективных возбуждений, позволяет предсказывать временную эволюцию системы после квантового скачка. Данный подход базируется на точном решении модели, что позволяет отслеживать изменения во времени различных физических величин, таких как плотность энергии и корреляционные функции. Исследование коллективных возбуждений, в частности, амплитудного мода, играет ключевую роль в понимании механизмов релаксации и установления нового равновесного состояния. Полученные предсказания позволяют не только описывать поведение системы вблизи момента скачка, но и прогнозировать ее дальнейшее развитие, определяя, насколько быстро и каким образом энергия перераспределяется между различными модами.

Анализ перераспределения энергии между различными модами системы после квантового взрыва позволяет понять, каким образом энергия высвобождается из начального возбуждения и распределяется по другим степеням свободы. Исследование показывает, что система, изначально находящаяся в неравновесном состоянии, стремится к новому состоянию, которое может быть близко к тепловому равновесию, хотя характер этого процесса может отличаться от классической тепловой релаксации. В ходе эволюции наблюдается перетекание энергии между различными модами, определяемыми коллективными возбуждениями, что приводит к формированию нового энергетического спектра и, в конечном итоге, к установлению нового стационарного состояния. Понимание этого механизма перераспределения энергии имеет ключевое значение для описания динамики неравновесных систем и может быть применено к изучению широкого круга физических явлений.

Предложенный подход, основанный на анализе коллективных возбуждений и методе Бете, служит надежным эталоном для проверки приближений, используемых при изучении более сложных систем. Точность полученных результатов позволяет оценить допустимость различных упрощений, часто применяемых в моделях, описывающих реальные физические системы, где аналитическое решение становится недостижимым. Возможность сопоставления численных расчетов с теоретическими предсказаниями, полученными с помощью строгого метода, предоставляет ценную информацию о пределах применимости приближенных схем и помогает оптимизировать стратегии моделирования. Таким образом, данная работа не только проливает свет на динамику неравновесных систем, но и способствует развитию более эффективных и надежных методов для изучения широкого спектра физических явлений.

Исследования показывают, что амплитудный мод, предсказанный теоретической моделью, может быть экспериментально зафиксирован в материалах, подобных Cs₂CoCl₄. Этот материал характеризуется отклонением анизотропии, равным приблизительно Δ ≈ 0.12, что создает благоприятные условия для проявления данного колебательного режима. Наблюдение амплитудного мода в Cs₂CoCl₄ стало бы важным подтверждением теоретических предсказаний и позволило бы глубже понять механизмы релаксации и перераспределения энергии в квантовых системах.

Соединение теоретических построений с измеримыми величинами открывает новые возможности для углубленного понимания неравновесной динамики в различных физических системах. Анализ коллективных возбуждений, в частности, позволяет предсказывать временную эволюцию системы после квантового скачка, выявляя механизмы перераспределения энергии между различными модами. Связь между теоретическими предсказаниями и экспериментально доступными параметрами, такими как амплитудный мод в материалах вроде Cs₂CoCl₄, где анизотропия составляет Δ ≈ 0.12, позволяет не только проверить адекватность теоретической модели, но и применить полученные результаты к изучению более сложных систем, где точные решения недоступны. Это создает основу для валидации приближенных методов и расширяет границы нашего понимания процессов, происходящих в неравновесных условиях, что имеет значение для широкого спектра физических явлений.

Исследование, представленное в данной работе, демонстрирует, что системы, находящиеся в критической фазе, подобны садам, где даже незначительные возмущения могут породить сложные, резонирующие колебания. Авторы, исследуя амплитудные моды в одномерной модели XXZ, выявили, что эти колебания, возникающие под воздействием квантовых сдвигов, являются проявлением внутренней сложности системы. Как говорил Нильс Бор: «Противоположности не отменяют друг друга, а дополняют». Именно это дополнение, взаимодействие различных аспектов системы, создает её устойчивость и способность к адаптации. В данном случае, амплитудные моды, являясь ответом на внешние воздействия, демонстрируют, что устойчивость системы не в её изоляции, а в способности к внутреннему приспособлению и прощению ошибок.

Что Дальше?

Наблюдение слабо затухающего колебания амплитуды в критической фазе — это не триумф моделирования, а скорее признание ее неполноты. Вместо того, чтобы строить идеальные системы, необходимо признать, что каждое архитектурное решение — это пророчество о будущей точке отказа. Возбуждение этого режима посредством квантовых скачков лишь подчеркивает, что истинная устойчивость начинается там, где заканчивается уверенность в предсказуемости.

Перспективы не кроются в усовершенствовании численных методов, а в понимании того, как эти коллективные возбуждения взаимодействуют с более сложными, неупорядоченными системами. Рассматривая модель XXZ как лишь один фрагмент более широкой экосистемы, возникает вопрос: как эти амплитудные моды ведут себя в присутствии диссипации, взаимодействий дальнего радиуса действия или, что более вероятно, в реальности, где идеальных параметров не существует?

Мониторинг этих колебаний — это не столько измерение, сколько способ бояться осознанно. Вместо того, чтобы стремиться к полному контролю, следует сосредоточиться на создании систем, способных к самовосстановлению и адаптации. В конечном итоге, истинная ценность этой работы заключается не в выявлении очередного режима, а в признании неизбежной сложности и непредсказуемости мира, в котором мы живем.

Оригинал статьи: https://arxiv.org/pdf/2601.20926.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-31 05:47