Спутанность в искривленном пространстве: цифровое моделирование и новые горизонты

Автор: Денис Аветисян

В статье представлены численные расчеты и аналитические исследования спутанности квантовых полей в различных искривленных пространствах, проливающие свет на связь между граничными и объемными теориями.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Энтропия запутанности демонстрирует зависимость от квадрата радиуса AdS <span class="katex-eq" data-katex-display="false">R^{2}</span>, подтверждая закон площади, при котором энтропия пропорциональна <span class="katex-eq" data-katex-display="false">R^{2}</span>, а наклон этой зависимости, в свою очередь, функционально связан с величиной радиуса AdS <span class="katex-eq" data-katex-display="false">L</span>. — Энтропия запутанности демонстрирует зависимость от квадрата радиуса AdS $R^{2}$ , подтверждая закон площади, при котором энтропия пропорциональна $R^{2}$ , а наклон этой зависимости, в свою очередь, функционально связан с величиной радиуса AdS $L$ .

Численное вычисление мер спутанности, таких как энтропия спутанности и логарифмическая негативность, в пространствах AdS4 и AdS3 с использованием метода репликации и расширения теплового ядра.

Несмотря на значительный прогресс в понимании квантовой запутанности, ее количественная оценка в искривленных пространствах остается сложной задачей. В работе ‘Numerical Computations of Entanglement Measures in Curved Space’ представлены численные и аналитические вычисления энтропии запутанности и логарифмической негативности для квантовых полей в различных геометриях, включая $AdS_4$ и $AdS_3$ . Используя такие методы, как репликация, разложение по тепловому ядру и сферические гармоники, авторы исследуют связь между граничными и объемными теориями, получая результаты, сопоставимые с коэффициентами теплового ядра. Какие новые аспекты соответствия $AdS/CFT$ могут быть раскрыты при дальнейшем изучении влияния кривизны пространства на квантовую запутанность?

Спутанность и парадокс пространства-времени: новые горизонты понимания

Спутанность, являясь одним из фундаментальных принципов квантовой механики, ставит под сомнение классическое понимание пространства-времени и информации. В то время как классическая физика предполагает локальность — то есть, что объект может быть подвержен влиянию только непосредственного окружения — квантовое сцепление демонстрирует мгновенную корреляцию между частицами, вне зависимости от расстояния между ними. Этот феномен, предсказанный теоретически и подтвержденный экспериментально, подразумевает, что информация может передаваться быстрее скорости света, что противоречит основным принципам теории относительности Эйнштейна. Более того, сцепление указывает на нелокальную природу реальности, ставя вопрос о том, как информация закодирована и передается на квантовом уровне, и требует переосмысления привычных представлений о причинности и взаимодействии в физическом мире. $\Psi = \sum_{i} c_i |i \rangle$

Вычисление энтропии запутанности, ключевой меры квантовой корреляции, представляет значительные трудности для традиционных методов квантовой теории поля. Эта сложность обусловлена тем, что стандартные подходы, разработанные для описания локальных взаимодействий, оказываются недостаточно эффективными при работе с нелокальными корреляциями, характерными для запутанных состояний. В частности, попытки вычислить энтропию запутанности для систем, состоящих из множества частиц — например, в конденсированных средах или в космологии — приводят к расходящимся интегралам и требуют введения процедур регуляризации, которые не всегда однозначны и могут вносить искусственные зависимости. Более того, точное определение границы между запутанной и незапутанной областями в многочастичных системах представляет собой концептуальную проблему, усугубляющую вычислительные трудности. В результате, для изучения энтропии запутанности в сложных квантовых системах необходимы новые инструменты и подходы, выходящие за рамки стандартной квантовой теории поля.

Сложность вычисления энтропии запутанности, ключевой характеристики квантовой корреляции, обусловлена фундаментальными особенностями самого явления. Запутанность по своей природе нелокальна, то есть корреляции между частицами не ограничены пространством и не могут быть объяснены классическим представлением о причинности. Более того, описание систем, состоящих из большого числа взаимодействующих частиц — так называемых многочастичных систем — представляет собой колоссальную вычислительную задачу. Традиционные методы квантовой теории поля испытывают затруднения при моделировании таких систем, поскольку необходимо учитывать бесконечное число взаимодействий между частицами. Именно сочетание нелокальности запутанности и сложности многочастичных систем делает точное вычисление энтропии запутанности чрезвычайно трудным, требуя разработки принципиально новых теоретических и вычислительных инструментов для исследования квантовых корреляций.

Энтропия запутанности скалярного поля в сфере в плоском пространстве-времени линейно возрастает с квадратом радиуса <span class="katex-eq" data-katex-display="false">R^2</span>. — Энтропия запутанности скалярного поля в сфере в плоском пространстве-времени линейно возрастает с квадратом радиуса $R^2$ .

Голография и геометрический расчёт запутанности: новый взгляд на пространство

Корреспонденция AdS/CFT представляет собой гипотезу о дуальности между теорией гравитации, определенной в пространстве Анти-де Ситтера (AdS), и конформной теорией поля (CFT), существующей на границе этого пространства. Пространство AdS характеризуется постоянной отрицательной кривизной, что приводит к гиперболической геометрии. CFT, напротив, описывает квантовую теорию поля, инвариантную относительно конформных преобразований. Эта дуальность предполагает, что любые физические величины, вычисляемые в одной теории, могут быть сопоставлены с соответствующими величинами в другой. В частности, вычисление свойств CFT в сильных взаимодействиях может быть сведено к решению задач в слабой гравитации в пространстве AdS, что делает данный подход мощным инструментом для изучения сложных квантовых систем. Формально, соответствие устанавливает эквивалентность между $n$ -мерным пространством AdS и $(n-1)$ -мерной CFT.

В рамках соответствия AdS/CFT, вычисление энтропии запутанности в конформной теории поля (CFT) осуществляется посредством определения площади минимальной поверхности (поверхности Риччи-Такхаши или RT-поверхности) в пространстве Анти-де Ситтера (AdS). Эта RT-поверхность определяется как поверхность, ограниченная областью, для которой вычисляется энтропия запутанности в CFT. Площадь этой минимальной поверхности напрямую пропорциональна энтропии запутанности, что позволяет преобразовывать задачу вычисления энтропии в геометрическую задачу нахождения экстремальной поверхности в AdS пространстве. $S_{EE} = \frac{A_{min}}{4G_N}$ , где $S_{EE}$ — энтропия запутанности, $A_{min}$ — площадь минимальной поверхности, а $G_N$ — ньютоновская гравитационная постоянная.

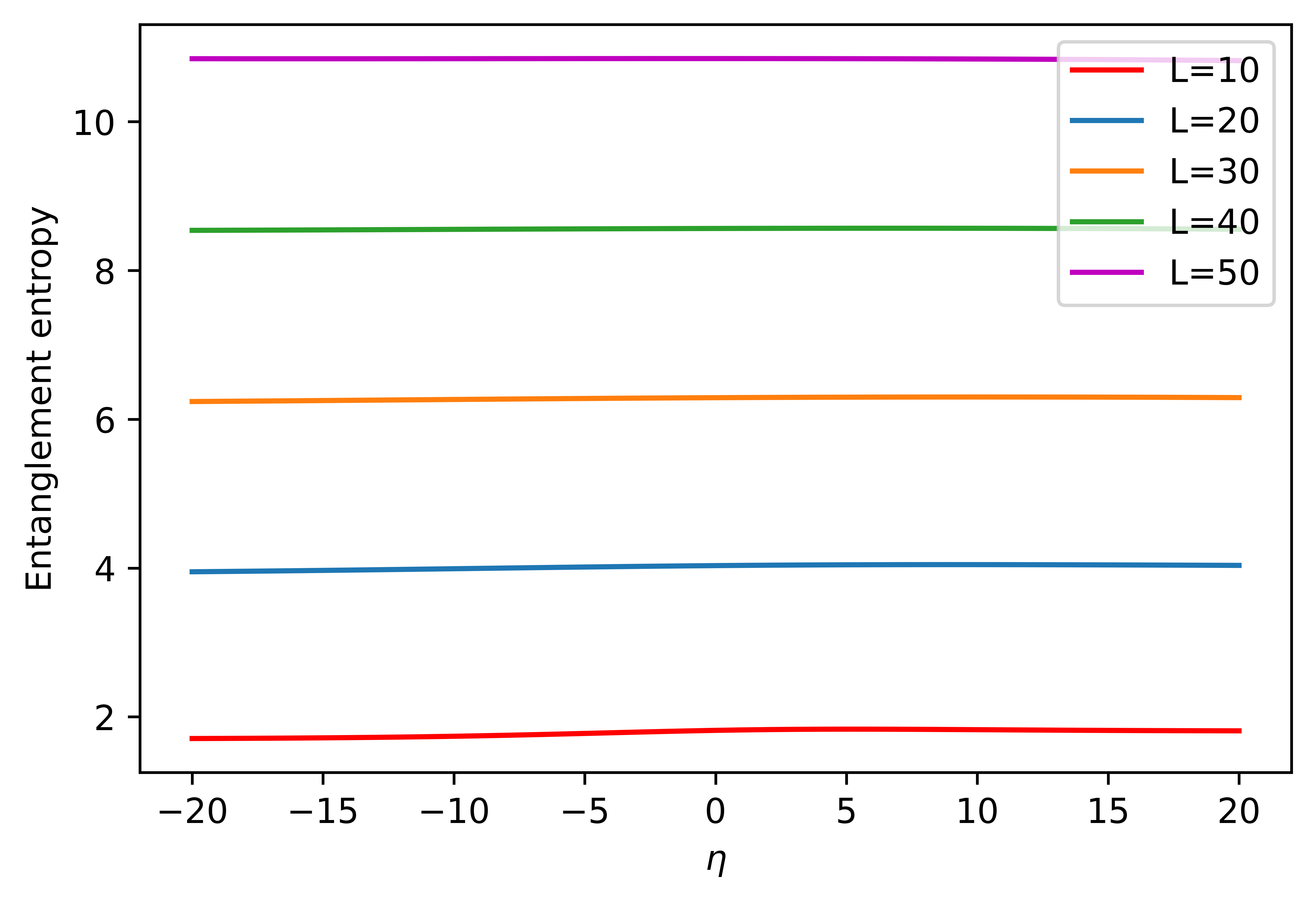
Использование координат, таких как глобальные координаты AdS (Anti-de Sitter), позволяет проводить точные вычисления минимальных поверхностей, необходимых для расчета энтропии запутанности в соответствующей конформной полевой теории (CFT). Проведенные вычисления подтверждают ожидаемую зависимость закона площади для энтропии запутанности как для скалярных, так и для векторных полей в пространстве AdS4. Аналогичные расчеты внутри поверхностей Риендере-Такахаши (RT) в пространстве AdS3 также подтверждают данную зависимость, что обеспечивает важную проверку соответствия AdS/CFT и позволяет исследовать свойства запутанности в рамках гравитационной теории. Математически, энтропия запутанности $S$ пропорциональна площади RT поверхности $A$ , то есть $S = A/[4G_N]$ , где $G_N$ — ньютоновская гравитационная постоянная.

Энтропия зацепленности калибровочного поля внутри поверхности Ричи-Тёрстона в глобальном <span class="katex-eq" data-katex-display="false">AdS_3</span> пространстве зависит от параметра LL. — Энтропия зацепленности калибровочного поля внутри поверхности Ричи-Тёрстона в глобальном $AdS_3$ пространстве зависит от параметра LL.

Аналитические и численные подходы к расчёту энтропии запутанности: преодолевая ограничения

Метод реплик представляет собой аналитический подход к вычислению энтропии запутанности, основанный на связи между энтропией запутанности и энтропией Рени. В рамках этого метода, рассматривается $n$ -кратное копирование рассматриваемой квантовой системы, после чего вычисляется $n$ -я энтропия Рени $S_n$ . Энтропия запутанности $S$ затем извлекается как предел $S = \lim_{n \to 1} \frac{1}{1-n} S_n$ . Этот метод позволяет преобразовать задачу вычисления энтропии запутанности в более удобную задачу вычисления энтропии Рени, которая часто может быть найдена аналитически, особенно в конформных полевых теориях.

Метод теплового ядра представляет собой альтернативный аналитический подход к вычислению энтропии запутанности, позволяющий выразить её в виде разложения в ряд. В рамках этого метода, энтропия запутанности выражается через трассировку теплового ядра $K(x, x')$ по области, ограничивающей подсистему A. Разложение осуществляется по степеням ε, где ε является малым параметром, связанным с ультрафиолетовым обрезанием. Каждый член этого разложения соответствует вкладу определённого порядка в ультрафиолетовом расширении энтропии, позволяя получать приближённые значения энтропии с заданной точностью. Данный метод особенно полезен в случаях, когда прямые вычисления через репликацию затруднены или невозможны.

Численные методы, использующие системы координат, такие как координаты собственного расстояния (Proper Distance Coordinates), являются необходимыми для расчета энтропии запутанности в сложных геометриях, где аналитические решения недоступны. Эти методы позволяют дискретизировать пространство и аппроксимировать интегралы, необходимые для вычисления энтропии, обеспечивая возможность получения результатов даже в ситуациях, когда точное решение невозможно получить. Применение координат собственного расстояния особенно эффективно, поскольку они упрощают вычисление геодезических расстояний, критичных для определения областей, участвующих в вычислении энтропии. Выбор подходящей дискретизации и экстраполяции результатов к пределу бесконечно малого шага сетки является ключевым аспектом обеспечения точности численных расчетов.

Валидность аналитических и численных методов расчета энтропии запутанности подтверждается их способностью последовательно выявлять универсальный член в выражении для энтропии. Для скалярных полей в глобальном AdS4 пространстве этот член имеет коэффициент, равный -1/90. Важно отметить, что в пределе $L \rightarrow \in fty$ , где $L$ — радиус пространства AdS, полученное значение коэффициента совпадает с соответствующим значением для плоского пространства, что служит дополнительным подтверждением корректности используемых подходов и их применимости к различным геометрическим конфигурациям.

Энтропия запутанности демонстрирует тенденцию к стабилизации при уменьшении интервала η между дискретными индексами <span class="katex-eq" data-katex-display="false"> j </span> при <span class="katex-eq" data-katex-display="false"> L=10 </span>, хотя начальное резкое снижение сохраняется. — Энтропия запутанности демонстрирует тенденцию к стабилизации при уменьшении интервала η между дискретными индексами $j$ при $L=10$ , хотя начальное резкое снижение сохраняется.

Исследуя пространство-время и за его пределами: расширяя горизонты понимания

Применение разработанных методов к пространству де Ситтера (dS), описываемому метрикой dS4 Static Patch, позволяет исследовать структуру квантовой запутанности на космологических горизонтах. Данный подход предполагает изучение корреляций между квантовыми состояниями, находящимися за пределами наблюдаемого космологического горизонта, что дает возможность лучше понять природу этих границ и их влияние на наблюдаемую Вселенную. Исследование структуры запутанности в dS пространстве имеет ключевое значение для понимания ранней Вселенной, эпохи инфляции и природы темной энергии, поскольку позволяет установить связь между квантовыми флуктуациями и геометрией пространства-времени. Полученные результаты могут пролить свет на фундаментальные вопросы космологии и квантовой гравитации, раскрывая глубокую взаимосвязь между квантовой механикой и общей теорией относительности.

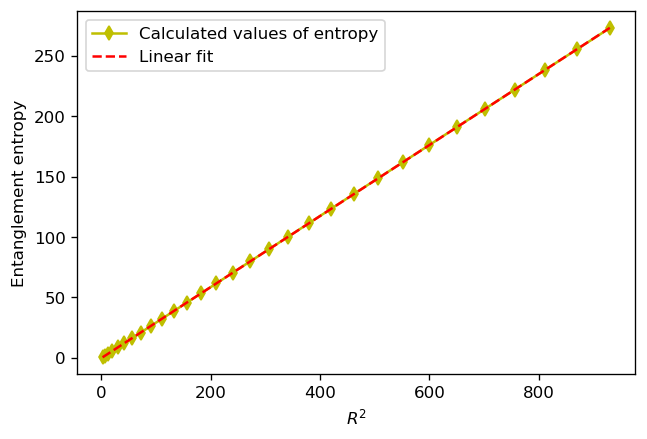
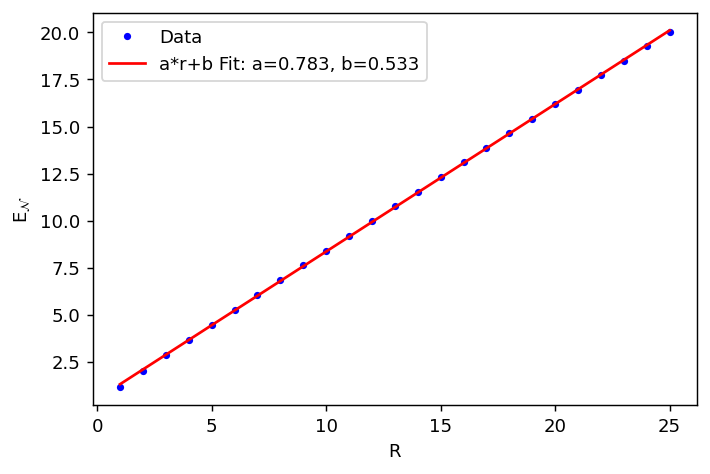
Для более детального изучения запутанности, помимо стандартных измерений энтропии, применяются концепции, такие как Логарифмическая Негативность. Данный показатель позволяет улавливать более тонкие аспекты квантовой запутанности, недоступные при использовании лишь энтропии. Исследования показали, что для скалярных полей в плоском пространстве Логарифмическая Негативность демонстрирует линейную зависимость от радиуса $R$ . Это означает, что с увеличением рассматриваемой области, степень запутанности между её частями растёт пропорционально её размеру, что указывает на фундаментальную связь между геометрией пространства и квантовыми корреляциями. Такое поведение позволяет глубже понять структуру вакуума и природу квантовых полей, выходя за рамки классического представления о пространстве-времени.

Для всестороннего анализа запутанности, являющейся ключевым свойством квантовых систем, необходимы специализированные математические инструменты. Одним из таких инструментов является разложение Шмидта, позволяющее представить сложное квантовое состояние в виде суммы произведений векторов, описывающих отдельные подсистемы. Этот метод позволяет выявить корреляции между частицами, даже когда они пространственно разделены, и количественно оценить степень их запутанности. Разложение Шмидта преобразует исходное состояние в более простую форму, удобную для вычислений и анализа, позволяя извлекать информацию о структуре и свойствах запутанности, а также устанавливать связь между квантовыми корреляциями и геометрией пространства-времени. Применение этого метода позволяет углубить понимание фундаментальных аспектов квантовой механики и ее связи с теорией гравитации.

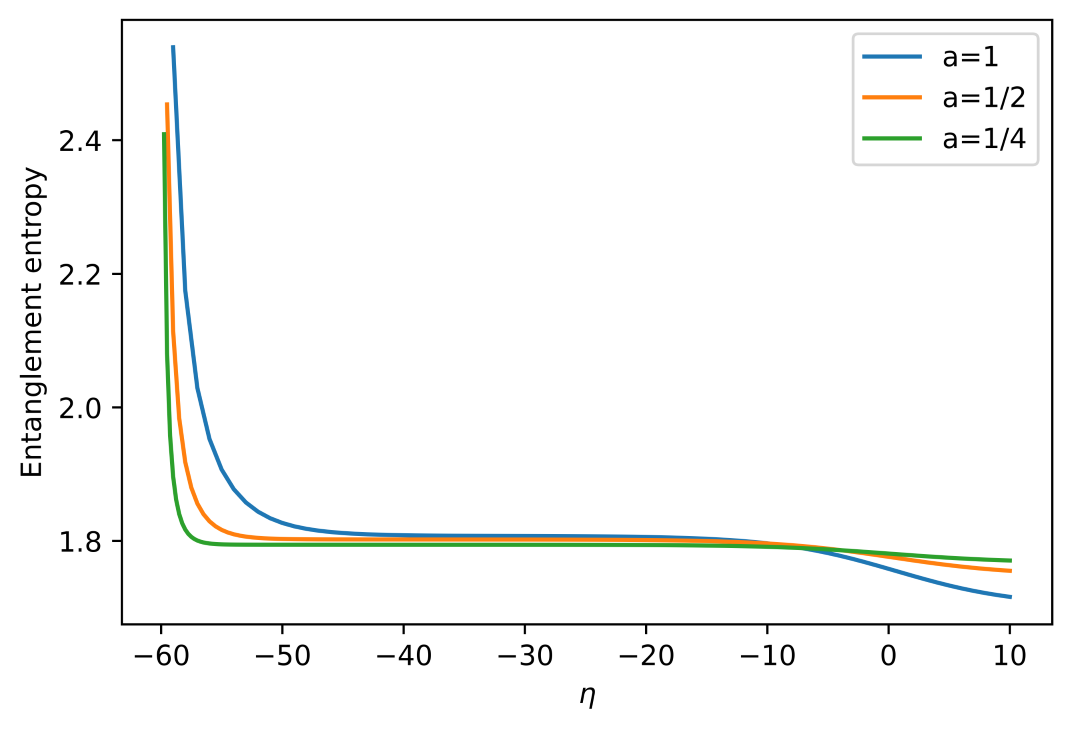
Проведенные вычисления выявили связь между конформной аномалией и структурой квантовой запутанности, демонстрируя глубокую взаимосвязь между запутанностью, геометрией пространства-времени и квантовой теорией поля. В частности, анализ отрицательной логарифмической энтропии $LogNeg$ для скалярных полей внутри поверхностей Римана-Тёрстона (RT) в трехмерном пространстве Анти-де Ситтера (AdS₃) показал, что она остается приблизительно постоянной, не зависящей от координаты η. Этот результат указывает на то, что степень запутанности, измеряемая с помощью $LogNeg$ , не претерпевает изменений при варьировании временной координаты, что имеет важные последствия для понимания природы пространства-времени и его связи с квантовыми явлениями, а также для построения голографических моделей космологических горизонтов.

В 2+1-мерном пространстве отрицательная логарифмическая энтроплика для скалярных полей на круглой энтропликающей поверхности линейно зависит от радиуса <span class="katex-eq" data-katex-display="false">RR</span>. — В 2+1-мерном пространстве отрицательная логарифмическая энтроплика для скалярных полей на круглой энтропликающей поверхности линейно зависит от радиуса $RR$ .

Данное исследование, посвященное численному вычислению мер запутанности в искривленных пространствах, подчеркивает сложность перехода от теоретических построений к практическим результатам. Автор демонстрирует, как методы вроде репликации и расширения теплового ядра позволяют исследовать взаимосвязь между граничными и объемными теориями, что является ключевым для понимания AdS/CFT соответствия. Как отмечал Юрген Хабермас: «Коммуникативное действие — это действие, ориентированное на достижение взаимопонимания». В контексте данной работы, стремление к точному численному моделированию можно рассматривать как форму коммуникации с фундаментальными законами физики, где точность вычислений является необходимым условием для достижения взаимопонимания и прогресса в области квантовой гравитации. Эффективность без морали — иллюзия, и в науке, точность без осмысления фундаментальных принципов — лишь ускорение без направления.

Куда же дальше?

Представленные вычисления, хоть и демонстрируют возможности численного анализа мер запутанности в искривлённых пространствах, лишь подчёркивают глубину нерешённых вопросов. Особенно остро стоит проблема связи между ультрафиолетовыми расходимостями и конформными аномалиями — попытки “приручить” бесконечности, похоже, лишь множат их новые формы. Чрезмерное увлечение технической точностью не должно заслонять фундаментальный вопрос: что эти расходимости говорят о природе самой реальности, о границах применимости наших теоретических инструментов?

Перспективы дальнейших исследований, вероятно, лежат в области поиска более элегантных, концептуально ясных методов регуляризации. Простое увеличение вычислительной мощности не решит проблему, если мы не поймём, что именно скрывается за кажущейся математической сложностью. Важно помнить, что каждый алгоритм несет в себе определенное мировоззрение, и автоматизация без этической рефлексии — это ускорение без направления.

Наконец, необходимо более тщательно исследовать связь между AdS/CFT корреспонденцией и физикой конденсированных сред. Возможно, ключи к пониманию квантовой гравитации лежат не в космологических масштабах, а в микроскопическом мире сильно коррелированных систем. Ведь, в конечном счёте, ценности закладываются в код, даже когда мы их не видим.

Оригинал статьи: https://arxiv.org/pdf/2601.21566.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-31 09:10