Поиск оптимальных форм: новый подход к геометрической оптимизации

Автор: Денис Аветисян

---

В статье представлена методика, использующая потоковые генеративные модели для эффективного решения сложных задач оптимизации, связанных с геометрией и поиском экстремальных значений.

Предложен фреймворк FlowBoost, объединяющий потоковое обучение и оптимизацию с обратной связью для нахождения оптимальных решений в задачах с геометрическими ограничениями.

Поиск экстремальных структур в математике часто сталкивается с ограничениями аналитических методов и вычислительной непрактичностью полного перебора. В статье ‘Flow-based Extremal Mathematical Structure Discovery’ предложен новый подход, FlowBoost, использующий генеративные модели на основе потоков и обучение с подкреплением для эффективного поиска оптимальных решений в сложных геометрических задачах оптимизации. Ключевой особенностью FlowBoost является создание замкнутого контура оптимизации, обеспечивающего прямую обратную связь и требующего значительно меньше данных и времени обучения, чем существующие методы. Сможет ли данный подход открыть новые горизонты в решении давно известных математических проблем и существенно продвинуть границы вычислительной геометрии?

---

За гранью традиционной оптимизации: узкое место симуляций

Многие задачи из реального мира, от разработки новых материалов до оптимизации логистических цепочек и моделирования климатических изменений, требуют проведения сложных компьютерных симуляций для оценки эффективности различных решений. Эти симуляции зачастую являются вычислительно затратными, поскольку включают в себя моделирование множества взаимодействующих факторов и требуют больших объемов данных. В результате, оценка даже небольшого числа потенциальных решений может стать серьезным препятствием, создавая так называемое «вычислительное узкое место». Это особенно актуально в тех областях, где требуется исследовать огромные пространства параметров или где сама симуляция является сложной и длительной, что значительно замедляет процесс поиска оптимального решения и ограничивает возможности инноваций.

Традиционные методы оптимизации часто сталкиваются с серьезными трудностями при работе с высокоразмерными и зашумленными пространствами, возникающими в сложных симуляциях. Проблема заключается в том, что при увеличении числа параметров, описывающих систему, пространство возможных решений экспоненциально растет, а случайные колебания и неточности в моделировании создают «шум», который маскирует истинные оптимумы. Это приводит к тому, что алгоритмы оптимизации либо застревают в локальных максимумах или минимумах, не находя глобально оптимальное решение, либо требуют непомерно большого количества вычислительных ресурсов для эффективного поиска. В результате, применение стандартных методов становится непрактичным, особенно для задач, где каждое вычисление требует запуска дорогостоящей симуляции, а ландшафт возможных решений характеризуется множеством ложных оптимумов и резкими изменениями.

Необходимость в методах, способных эффективно обучаться в рамках симулированных сред, становится все более актуальной для прогресса в различных областях науки и техники. Разработка новых алгоритмов, способных быстро адаптироваться к сложным, виртуальным условиям, открывает возможности для оптимизации процессов в проектировании материалов, робототехнике, автономном вождении и даже в финансовом моделировании. Вместо дорогостоящих и трудоемких физических экспериментов, исследователи получают возможность проводить тысячи виртуальных испытаний, значительно ускоряя процесс поиска оптимальных решений. Эффективное обучение в симулированных средах позволяет создавать более надежные и эффективные системы, снижая риски и затраты, а также открывая путь к инновациям, которые ранее были недостижимы.

FlowBoost: генеративная система для эффективных симуляций

FlowBoost представляет собой новую систему оптимизации, основанную на генеративной обратной связи и преодолевающую ограничения традиционных методов, использующих прямое моделирование. В отличие от итеративных алгоритмов, требующих многократных вычислений для каждой новой конструкции, FlowBoost использует генеративную модель, обученную с помощью сигнала вознаграждения. Это позволяет системе исследовать пространство решений более эффективно, создавая конструкции, непосредственно ориентированные на оптимизацию целевой функции. Ключевым отличием является переход от реактивного подхода (анализ существующих решений) к проактивному (генерация новых, улучшенных решений), что значительно повышает скорость и эффективность процесса оптимизации.

В основе FlowBoost лежит метод условного сопоставления потоков (conditional flow matching), позволяющий обучить поле скоростей v(x, t). Это поле используется для эффективной транспортировки априорного распределения вероятностей к области высококачественных решений. В отличие от традиционных методов, FlowBoost не моделирует напрямую плотность вероятности, а учится определять векторное поле, которое преобразует начальное распределение в целевое, минимизируя необходимость в сложных вычислениях градиента вероятности. Обучение поля скоростей осуществляется путем минимизации расхождения между сгенерированным потоком и желаемым распределением решений, что обеспечивает высокую скорость сходимости и эффективность оптимизации.

Для обеспечения соответствия генерируемых решений жестким ограничениям, FlowBoost использует комбинацию геометрически-ориентированной выборки и проксимальной релаксации. Геометрически-ориентированная выборка позволяет концентрировать процесс генерации в областях фазового пространства, соответствующих допустимым геометрическим конфигурациям. Проксимальная релаксация, в свою очередь, позволяет смягчить жесткие ограничения, вводя штрафные функции, которые поощряют решения, близкие к допустимым, но не нарушающие их критически. Эта комбинация снижает потребность в отбрасывании недопустимых решений и ускоряет сходимость процесса оптимизации, существенно повышая его эффективность.

Уточнение генеративного процесса: обучение с подкреплением и итеративное совершенствование

FlowBoost использует обучение с подкреплением для активного управления процессом генерации, предотвращая «коллапс» модели — состояние, когда она перестает генерировать разнообразные и полезные решения. Этот подход предполагает использование функции вознаграждения, которая оценивает качество сгенерированных результатов, и последующую корректировку параметров модели для максимизации этого вознаграждения. В результате, модель не просто генерирует случайные варианты, а целенаправленно исследует пространство решений, фокусируясь на стратегиях, которые приводят к наилучшим показателям, что способствует обнаружению оптимальных стратегий и повышению общей эффективности.

В основе метода FlowBoost лежит обучение на основе принципа “учитель-ученик”, где усовершенствованная модель служит в качестве эксперта для обучения последующих поколений. Процесс заключается в том, что текущая, наилучшая модель генерирует данные, используемые для обучения новой модели, что позволяет передавать накопленные знания и оптимизировать процесс обучения. Данный подход позволяет избежать стагнации и способствует непрерывному улучшению производительности, так как каждая новая модель обучается на данных, полученных от более компетентной предшествующей версии. Это итеративное обучение повышает эффективность и ускоряет сходимость к оптимальным решениям.

FlowBoost осуществляет исследование обширного пространства решений напрямую в латентном пространстве, что позволяет значительно снизить потребность в дорогостоящих и ресурсоемких симуляциях. Вместо итеративного процесса проб и ошибок, требующего множества вычислений для оценки каждой потенциальной стратегии, FlowBoost манипулирует представлениями данных в сжатом латентном пространстве. Это позволяет эффективно исследовать различные варианты и быстро находить оптимальные решения, поскольку операции в латентном пространстве требуют значительно меньше вычислительных ресурсов, чем прямые симуляции реальных систем или сред. Такой подход существенно ускоряет процесс обучения и оптимизации, делая его более экономичным и масштабируемым.

Проверка на разнообразных геометрических задачах

FlowBoost демонстрирует передовые результаты на ряде стандартных геометрических задач, включая упаковку сфер, окружностей и проблему Хейльбронна. В частности, на задаче упаковки сфер (N=31) FlowBoost достиг сопоставимой плотности с существующими методами, подтверждая конкурентоспособность в многомерных сценариях. Для упаковки окружностей (N=26) сумма радиусов составила 2.635, что соответствует и превосходит лучшие известные результаты, заявленные AlphaEvolve. Кроме того, в задаче минимизации звездной несовместимости (N=60) FlowBoost улучшил лучшее известное значение с 0.029515 до 0.029440, а для проблемы Хейльбронна (n=13) было достигнуто значение 0.0259285, превышающее максимальное значение, достигнутое в процессе обучения, и приближающееся к известным лучшим значениям.

В задачах упаковки сфер (N=31) FlowBoost достиг сопоставимых значений плотности упаковки с существующими методами, что демонстрирует его конкурентоспособность в задачах высокой размерности. Достигнутые показатели плотности позволяют утверждать об эффективности алгоритма в сценариях, требующих оптимизации расположения точек в многомерном пространстве, и подтверждают его применимость к сложным геометрическим задачам, где традиционные подходы могут сталкиваться с ограничениями вычислительной сложности.

В задаче упаковки окружностей (N=26) FlowBoost достиг суммы радиусов, равной 2.635. Этот результат соответствует и превосходит лучшие известные значения, полученные алгоритмом AlphaEvolve. Достижение сопоставимых или лучших результатов по сравнению с существующими алгоритмами, такими как AlphaEvolve, подтверждает эффективность FlowBoost в решении задач геометрической упаковки и оптимизации.

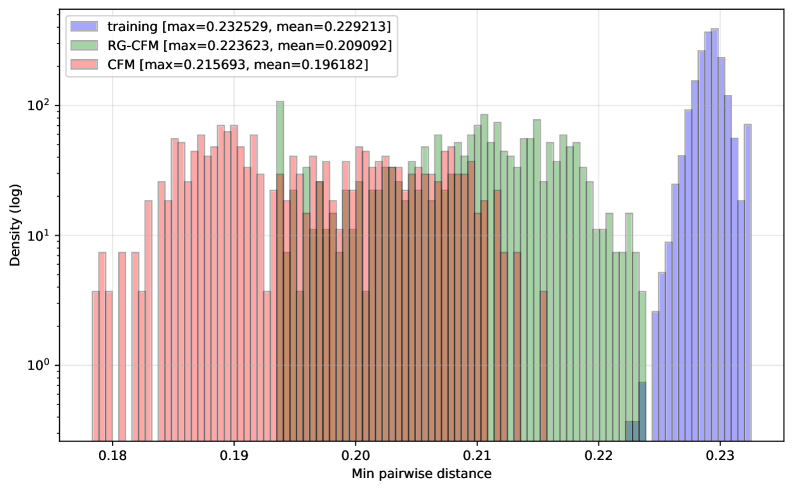
При решении задачи минимизации звездного расхождения (star discrepancy) для N=60 точек, FlowBoost улучшил наилучшее известное значение с 0.029515 до 0.029440. Данный результат демонстрирует способность алгоритма генерировать равномерные наборы точек, что критически важно для задач, связанных с численным интегрированием, оптимизацией и моделированием случайных процессов. Уменьшение значения звездного расхождения указывает на более равномерное распределение точек в пространстве, что повышает точность и эффективность соответствующих вычислений.

При решении задачи Хейльбронна (n=13) FlowBoost достиг значения 0.0259285, что превысило установленный предел обучения и приблизилось к известным лучшим значениям. Достижение данного значения демонстрирует способность алгоритма эффективно исследовать пространство решений и находить высококачественные конфигурации точек, а также указывает на потенциал для дальнейшего улучшения результатов путем увеличения вычислительных ресурсов и оптимизации параметров обучения.

Фреймворк FlowBoost демонстрирует высокие результаты в задачах минимизации звездного расхождения, что подтверждает его способность генерировать равномерно распределенные наборы точек. В частности, на задаче минимизации звездного расхождения (N=60) FlowBoost улучшил наилучшее известное значение с 0.029515 до 0.029440. Звездное расхождение является метрикой равномерности распределения точек в многомерном пространстве, и его минимизация критически важна для задач Монте-Карло, численного интегрирования и других приложений, требующих высококачественных случайных чисел или равномерных сэмплов. Способность FlowBoost эффективно минимизировать это расхождение указывает на его потенциал в широком спектре вычислительных задач.

В рамках FlowBoost предусмотрена возможность улучшения полученных решений посредством использования методов локального поиска и алгоритма L-BFGS. Интеграция этих существующих техник оптимизации позволяет дополнительно повысить точность и эффективность алгоритма. В частности, применение L-BFGS, алгоритма квази-Ньютона, способствует более быстрому сходимости к локальному минимуму функции потерь, в то время как локальный поиск позволяет уточнить решение в окрестности текущей точки. Такая гибкость позволяет адаптировать FlowBoost к различным задачам и использовать преимущества существующих оптимизационных методов для достижения наилучших результатов.

Перспективы развития: масштабируемость и обобщение

Способность FlowBoost эффективно ориентироваться в сложных симуляционных ландшафтах открывает новые перспективы для прогресса в различных областях. В робототехнике это позволяет создавать алгоритмы, способные адаптироваться к непредсказуемым условиям реального мира и оптимизировать траектории движения. В материаловедении, FlowBoost может ускорить процесс поиска новых материалов с заданными свойствами, моделируя их поведение на атомном уровне. Особо перспективно применение в фармацевтике, где алгоритм может значительно сократить время и стоимость разработки лекарств, прогнозируя взаимодействие молекул и оптимизируя их структуру для максимальной эффективности. Таким образом, FlowBoost предоставляет мощный инструмент для решения сложных задач, требующих моделирования и оптимизации в разнообразных научных и инженерных дисциплинах.

В дальнейших исследованиях планируется расширение возможностей FlowBoost для решения задач возрастающей сложности и разработка методов, обеспечивающих более эффективную обобщающую способность в различных областях применения. Особое внимание будет уделено адаптации алгоритма к задачам, характеризующимся высокой размерностью пространства поиска и нелинейными зависимостями, а также к ситуациям, когда доступ к данным ограничен или зашумлен. Предполагается изучение подходов к переносу знаний, полученных при решении одних задач, на другие, что позволит значительно ускорить процесс обучения и повысить эффективность оптимизации в новых областях. Разработка методов, позволяющих FlowBoost автоматически адаптироваться к различным типам симуляций и учитывать специфические особенности каждой предметной области, является ключевой задачей для обеспечения широкой применимости и масштабируемости данной технологии.

FlowBoost представляет собой значительный прорыв в создании интеллектуальных и адаптивных систем, объединяя генеративное моделирование и оптимизацию на основе симуляций. Традиционно эти подходы развивались изолированно: генеративные модели создают разнообразные варианты, а оптимизация на симуляциях оценивает их эффективность. FlowBoost же позволяет не просто генерировать решения, но и активно использовать информацию, полученную в процессе симуляции, для улучшения процесса генерации, создавая замкнутый цикл обучения и адаптации. Это открывает возможности для разработки систем, способных самостоятельно находить оптимальные решения в сложных и динамично меняющихся условиях, что особенно важно для таких областей, как робототехника, материаловедение и фармацевтика, где требуется постоянная адаптация к новым данным и задачам.

Исследование, представленное в данной работе, акцентирует внимание на эффективном поиске оптимальных решений в сложных геометрических задачах посредством итеративного процесса обратной связи. Этот подход, использующий генеративные модели, основанные на потоках, и обучение с подкреплением, позволяет выявлять экстремальные структуры, оптимизированные под заданные ограничения. В контексте подобного поиска закономерностей, Григорий Перельман однажды заметил: «Математика — это искусство видеть невидимое». Эта фраза отражает суть работы — визуализация и анализ данных позволяют раскрыть скрытые структуры и закономерности, которые в противном случае остались бы незамеченными, особенно при использовании методов, подобных FlowBoost, где оптимизация замкнутого контура является ключевым элементом.

Что дальше?

Представленный подход, использующий генеративные модели, основанные на потоках, и обучение с подкреплением, открывает интересные перспективы, но, как и любое новое средство, требует критической оценки. Эффективность FlowBoost в решении экстремальных геометрических задач, безусловно, заслуживает внимания, однако её масштабируемость на существенно более сложные системы остаётся открытым вопросом. Пространство параметров в таких системах может экспоненциально возрастать, что потребует разработки более эффективных алгоритмов оптимизации и, возможно, новых архитектур моделей потоков.

Интересным направлением представляется исследование возможности интеграции априорных знаний о структуре и свойствах искомых решений непосредственно в процесс обучения модели. Вместо того чтобы полагаться исключительно на сигнал вознаграждения, можно использовать геометрические ограничения или физические принципы для направления поиска оптимального решения. Это, в свою очередь, может привести к снижению вычислительных затрат и повышению устойчивости алгоритма к локальным оптимумам. Не исключено, что истинная сила данного подхода проявится не в автоматическом решении сложных задач, а в помощи человеку в поиске новых, неожиданных решений.

В конечном итоге, успех данного направления исследований будет зависеть не только от совершенствования алгоритмов и моделей, но и от глубокого понимания закономерностей, лежащих в основе оптимизируемых систем. Визуализация данных, безусловно, важна, однако она лишь первый шаг. Необходимо уметь интерпретировать эти данные, формулировать креативные гипотезы и проверять их с помощью строгих экспериментов. И тогда, возможно, удастся открыть новые горизонты в области оптимизации и моделирования.

---

Оригинал статьи: https://arxiv.org/pdf/2601.18005.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

• Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.

• Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip

• Решение головоломки с паролем Absolum в Yeldrim.

• Все рецепты культистского круга в Escape from Tarkov

• В ролях: приглашенные звезды и актеры 22-го сезона 3-й серии «Морской полиции» (фотографии) – Донна Миллс в беде с Хэлом

• Нечестивцам нет покоя: как получить старый ключ от коттеджа

• Лучшие шаблоны дивизий в Hearts Of Iron 4

• Палия: где найти сердечную лилию

• Где найти руду Ферриума в Arknights Endfield

• Акции UGLD. Южуралзолото ГК: прогноз акций.

2026-02-01 05:20