Танцующие сигналы: Интерференция в поисках новой физики

Автор: Денис Аветисян

Новые исследования показывают, что игнорирование интерференции между сигналами новой физики и стандартными процессами может искажать результаты экспериментов на коллайдерах.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Влияние интерференционных вкладов на распределение инвариантной массы демонстрирует, что при фиксированном сценарии новой физики наблюдаются различные вклады, особенно в пределе больших масс, а учет этих эффектов существенно изменяет общую форму распределения, подчеркивая важность их рассмотрения при анализе данных.

В статье рассматриваются интерференционные эффекты в процессах с участием скалярных резонансов и ди-бозонных/ди-хиггсовских финальных состояний, подчеркивая важность учета конечной ширины резонансов для корректного моделирования наблюдаемых распределений.

Несмотря на значительные успехи Стандартной модели, поиск новой физики требует точного моделирования процессов, включающих как фоновые, так и сигнальные события. В работе, посвященной ‘Interference effects in new physics searches’, рассматривается важная роль интерференционных эффектов между резонансными сигналами новой физики и стандартными процессами, которые часто игнорируются в теоретических расчетах и экспериментальных поисках. Пропущенные интерференционные эффекты могут приводить к искажению кинематических распределений и, как следствие, к неверной интерпретации результатов экспериментов на коллайдерах, особенно в контексте моделей с расширенными скалярными секторами. Насколько точное учет интерференции является критичным для надежного поиска за пределами Стандартной модели и какие новые подходы могут быть разработаны для более точного моделирования этих эффектов?

За гранью Стандартной модели: Поиск новой физики

Несмотря на впечатляющие успехи, Стандартная модель физики элементарных частиц оставляет без объяснения ряд фундаментальных явлений, указывая на существование более сложной реальности. Наблюдаемые темная материя и темная энергия, а также необъяснимая масса нейтрино, не находят места в рамках существующей теории. Кроме того, Стандартная модель не способна объяснить асимметрию между материей и антиматерией во Вселенной, а также природу гравитации, которая не интегрирована в эту структуру. Эти несоответствия, наряду с некоторыми аномалиями в экспериментах с распадом мюонов, побуждают ученых к поиску «Новой физики», подразумевающей существование частиц и взаимодействий, выходящих за рамки известного нам мира, и требующей пересмотра основополагающих принципов современной физики.

Высокоточные измерения, проводимые в современных физических экспериментах, всё чаще указывают на несоответствия между теоретическими предсказаниями Стандартной модели и наблюдаемыми явлениями. Эти расхождения, хотя и кажутся незначительными, требуют пересмотра фундаментальных принципов, лежащих в основе нашего понимания Вселенной. Косвенные поиски, основанные на анализе редких распадов частиц и аномальных магнитных моментов, также свидетельствуют о существовании новых частиц и взаимодействий, не предусмотренных в рамках существующей теории. Например, отклонения в свойствах мюонов, наблюдаемые в Фермилабе, могут быть предвестниками взаимодействия с неизвестными частицами, что требует дальнейшего изучения и разработки новых экспериментальных стратегий для подтверждения или опровержения этих гипотез. Эти поиски, хоть и сложны, представляют собой критически важный шаг к расширению границ нашего знания о фундаментальных законах природы.

Исследование сценариев «Новой Физики» представляется необходимым шагом для завершения целостной картины Вселенной. Современное понимание, основанное на Стандартной Модели, не способно объяснить ряд наблюдаемых явлений, таких как темная материя, темная энергия и асимметрия барионной материи. Поиск отклонений от предсказаний Стандартной Модели в экспериментах, проводимых на Большом адронном коллайдере и в других научных установках, может указать на существование новых частиц и взаимодействий, выходящих за рамки известной физики. Именно эти исследования способны пролить свет на фундаментальные вопросы о происхождении Вселенной, ее эволюции и составе, открывая новые горизонты в познании природы реальности и дополняя существующие теоретические рамки.

Поиск физики за пределами Стандартной модели неразрывно связан с углубленным изучением скалярных бозонов — фундаментальных частиц, предсказываемых многими теориями-расширениями. Эти частицы, в отличие от бозонов, переносящих силу, характеризуются нулевым спином и ответственны за механизм генерации массы других частиц, что является ключевым аспектом современной физики элементарных частиц. Исследования скалярных бозонов, включая гипотетический бозон Хиггса и его потенциальные аналоги, позволяют проверить предсказания новых моделей и понять, как устроена Вселенная на самом фундаментальном уровне. Их свойства, такие как масса, спин и взаимодействия, могут предоставить ценные подсказки о природе темной материи, темной энергии и других загадках, которые Стандартная модель не в силах объяснить. φ — типичное обозначение скалярного поля, описывающего поведение этих частиц, и детальное изучение этого поля открывает новые горизонты в понимании структуры материи и сил, управляющих ею.

Распределения инвариантной массы ди-бозонов демонстрируют вклад целевого процесса <span class="katex-eq" data-katex-display="false">pp \rightarrow H \rightarrow VV</span>, интерференцию со скалярным бозоном SM и фоновый вклад, показывая, что учет всех интерференционных членов (синяя линия) существенно влияет на наблюдаемый сигнал по сравнению с чистым сигналом (черная линия) или сигналом с интерференцией только от резонанса 125 ГэВ (красная линия). — Распределения инвариантной массы ди-бозонов демонстрируют вклад целевого процесса $pp \rightarrow H \rightarrow VV$ , интерференцию со скалярным бозоном SM и фоновый вклад, показывая, что учет всех интерференционных членов (синяя линия) существенно влияет на наблюдаемый сигнал по сравнению с чистым сигналом (черная линия) или сигналом с интерференцией только от резонанса 125 ГэВ (красная линия).

Резонансное производство: Раскрытие скрытых частиц

Производство резонансов является ключевым методом обнаружения новых частиц, основанным на создании нестабильных промежуточных состояний, которые быстро распадаются на обнаруживаемые конечные продукты. Этот процесс предполагает столкновение частиц с определенной энергией, приводящее к образованию резонанса — кратковременно существующей частицы, характеризующейся определенной массой и спином. Наблюдение пиков в распределениях продуктов распада по инвариантной массе позволяет идентифицировать резонансы и, следовательно, предсказывать существование новых частиц. Интенсивность этих пиков пропорциональна сечению образования и вероятности распада резонанса, что позволяет проводить количественный анализ и определять характеристики новых частиц.

Точное моделирование процессов резонансного производства новых частиц базируется на принципах квантовой теории поля (КТП) и формализма S-матрицы. КТП описывает частицы как возбуждения квантовых полей, а взаимодействия между ними — как обмен виртуальными частицами. Формализм S-матрицы позволяет рассчитывать вероятности различных процессов рассеяния и распада, связывая начальное и конечное состояния системы. В рамках этого подхода, S-матрица представляет собой оператор, действующий на асимптотические состояния частиц и определяющий амплитуду вероятности перехода из одного состояния в другое. Расчеты, выполняемые в рамках КТП и S-матрицы, используют $Feynman diagrams$ для визуализации и вычисления амплитуд взаимодействий, учитывая все возможные каналы распада и интерференции.

Для упрощения расчетов при изучении резонансного производства, часто применяется факторизованный подход. Суть метода заключается в разделении сложного процесса на два последовательных этапа: образование промежуточного резонансного состояния (производство) и его последующий распад на наблюдаемые частицы (распад). Математически, это выражается в виде произведения амплитуд для каждого этапа: $\mathcal{A} = \mathcal{A}_{prod} \cdot \mathcal{A}_{decay}$ . Такой подход позволяет значительно снизить вычислительную сложность, поскольку амплитуда полного процесса представляется как произведение более простых амплитуд, что особенно важно при анализе процессов с участием большого числа частиц.

В рамках факторизованного подхода к анализу процессов резонансного производства, ключевым является условие “он-шелльности” (on-shellness) промежуточных частиц. Данное условие подразумевает, что в каждом этапе процесса, описываемом диаграммами Фейнмана, энергия и импульс промежуточной частицы должны удовлетворять дисперсионному соотношению: $p^2 = E^2/c^2 - p^2c^2 = m^2c^4$ , где $p$ — импульс частицы, $E$ — её энергия, а $m$ — масса. Соблюдение этого условия эквивалентно тому, что промежуточная частица является реальной, а не виртуальной, и позволяет упростить расчеты амплитуды рассеяния, рассматривая каждый этап как независимое взаимодействие. Нарушение условия “он-шелльности” привело бы к появлению в расчетах нефизических вкладов и некорректным результатам.

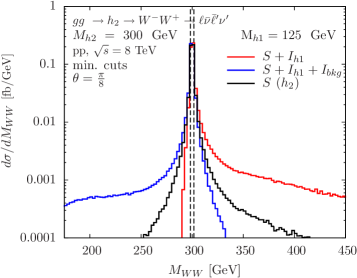
Анализ инвариантных масс при резонансно усиленном производстве двух Хиггсов демонстрирует, что учет размытия, вызванного конечным разрешением детектора, позволяет выделить чистые резонансы (зеленый), стандартный фон, а также вклад резонансов с корректной перешкалировкой связей (красный и розовый цвета) и полный вклад, включающий все интерференционные члены (синий), при нормализации к полному сечению рождения на уровне следующего за ведущим порядка (NLO), как показано в работе [27].

Интерференция и точность: Декодирование тонких сигналов

Интерференционные эффекты оказывают существенное влияние на процессы резонансного производства, приводя к модификации наблюдаемых распределений продуктов распада. В частности, при одновременном производстве нескольких резонансов или при наличии перекрывающихся каналов распада, амплитуды вероятностей для различных процессов интерферируют друг с другом. Это приводит к отклонениям от простых распределений, описываемых, например, функцией Брайт-Вигнера. Интенсивность резонансного сигнала может быть как усилена, так и ослаблена в зависимости от фазовых соотношений между интерферирующими амплитудами. Точное описание этих эффектов требует учета всех возможных каналов распада и соответствующих амплитуд, что является сложной задачей в теоретических расчетах.

Для точного описания наблюдаемых эффектов интерференции и резонансов в физике высоких энергий необходимы высокоточные теоретические расчеты. Эти расчеты часто выполняются в рамках теории возмущений, где используются поправки следующего порядка (Next-to-Leading Order, NLO). Поправки NLO учитывают дополнительные вклады в процессы рассеяния и распада частиц, которые не включаются в расчеты ведущего порядка. Включение NLO поправок позволяет существенно повысить точность предсказаний и сравнить их с экспериментальными данными, что критически важно для поиска отклонений от Стандартной модели и проверки теоретических моделей. Расчет NLO поправок является сложной задачей, требующей применения передовых вычислительных методов и значительных вычислительных ресурсов.

Схема комплексной массы является эффективным инструментом для учета распада частиц при проведении теоретических расчетов в физике высоких энергий. Вместо использования физической массы, которая требует решения сложного интеграла по фазовому пространству распада, схема комплексной массы заменяет физическую массу $m$ на комплексное значение $m + i\Gamma/2$ , где Γ — ширина распада. Это позволяет аналитически продолжить амплитуду рассеяния в комплексную плоскость, упрощая вычисление сечений и распределений, особенно вблизи порогов и резонансов. Применение схемы комплексной массы существенно облегчает учет интерференции между различными каналами распада и позволяет более точно моделировать наблюдаемые формы резонансов, например, отклонения от классического брейтивского распределения.

Оптическая теорема служит важной проверкой согласованности амплитуд рассеяния и интерференционных картин. Отклонения от стандартной $Breit-Wigner$ функции — наблюдаемые значительные искажения в распределениях по инвариантной массе — могут указывать на новую физику, выходящую за рамки Стандартной модели. Величина этих искажений может быть существенной и существенно влиять на стратегии поиска новых частиц и явлений, требуя модификации существующих алгоритмов анализа данных и поиска сигналов.

Анализ инвариантной массы дитопов в различных вариантах двух-хиггсовских моделей показывает, что различия в массах дополнительных скалярных частиц приводят к искажениям в спектрах, особенно заметным вдали от резонансных областей, при условии идеального разрешения детекторов <span class="katex-eq" data-katex-display="false">0\%</span>. — Анализ инвариантной массы дитопов в различных вариантах двух-хиггсовских моделей показывает, что различия в массах дополнительных скалярных частиц приводят к искажениям в спектрах, особенно заметным вдали от резонансных областей, при условии идеального разрешения детекторов $0\%$ .

Исследование сектора Хиггса: Модели и предсказания

Теоретические модели, такие как Двухдублетная модель Хиггса и Расширение с синглетом, предсказывают существование дополнительных скалярных бозонов, выходящих за рамки стандартной модели физики элементарных частиц. В то время как стандартная модель постулирует только один скалярный бозон — бозон Хиггса, эти расширения вводят новые частицы, которые могут проявляться в различных процессах и взаимодействиях. Эти дополнительные бозоны могут иметь различные свойства, включая массу, спин и заряды, что открывает широкие возможности для поиска новой физики в экспериментах на Большом адронном коллайдере и других ускорителях. Их обнаружение или установление ограничений на их свойства позволит проверить предсказания этих моделей и углубить понимание механизма спонтанного нарушения электрослабой симметрии.

Поиск новых скалярных бозонов, предсказываемых моделями, выходящими за рамки Стандартной модели, активно ведется в различных каналах распада. Особенно перспективными являются поиски событий с образованием двух бозонов Хиггса (Di-Higgs Production), где наблюдается корреляция между спинами частиц. Кроме того, исследуются распады, приводящие к образованию пар других векторных бозонов (Di-Boson Final States), таких как $Z$ или $W$ -бозоны, а также к паре топ-кварков (Di-Top Final States). Каждый из этих каналов обладает уникальной сигнатурой и чувствительностью к различным параметрам новых моделей, что позволяет комплексно исследовать пространство параметров и сузить область поиска за пределами Стандартной модели.

При изучении распадов нестабильных частиц, таких как дополнительные скалярные бозоны, предсказываемые различными моделями за пределами Стандартной модели, упрощение вычислений играет ключевую роль. В рамках приближения малой ширины распада (Narrow Width Approximation) считается, что ширина распада новой частицы значительно меньше её массы. Это позволяет рассматривать распад как последовательный процесс, в котором частица сначала распадается на промежуточные продукты, а затем эти продукты распадаются на наблюдаемые частицы. Такой подход значительно упрощает математический аппарат, позволяя более эффективно анализировать экспериментальные данные и извлекать информацию о параметрах новых частиц.

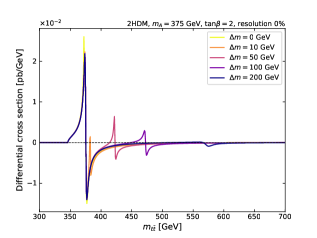
Высокоточные измерения электрослабых взаимодействий играют ключевую роль в ограничении параметров моделей, выходящих за рамки Стандартной модели. В частности, в сложных конфигурациях модели двух дублетов Хиггса (2HDM) наблюдается интересный феномен: резонансные вклады в распределение по инвариантной массе могут полностью компенсироваться интерференцией. Это означает, что точное моделирование этих эффектов имеет первостепенное значение, поскольку игнорирование интерференции может привести к ошибочной интерпретации экспериментальных результатов и ложным выводам о существовании новых частиц или отклонениях от предсказаний Стандартной модели. Тщательный анализ и учет этих тонких эффектов необходимы для надежного поиска новой физики за пределами известных взаимодействий.

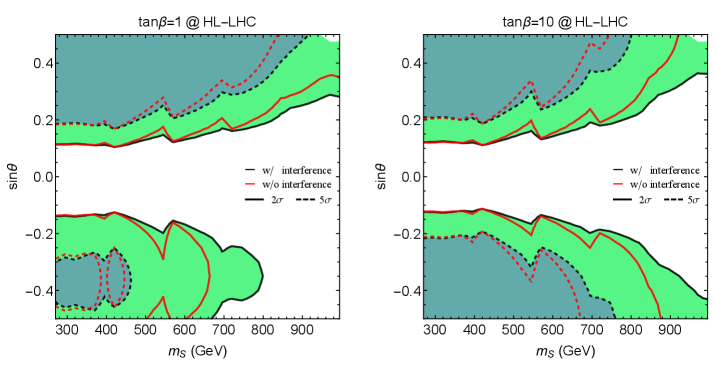
Прогнозы для каналов исключения и открытия на HL-LHC для расширения с синглетом в ди-хиггсном распаде, где синглет приобретает вакуумное ожидаемое значение, показывают значительные различия между случаями с учетом и без учета интерференций в зависимости от величины <span class="katex-eq" data-katex-display="false"> aneta</span>. — Прогнозы для каналов исключения и открытия на HL-LHC для расширения с синглетом в ди-хиггсном распаде, где синглет приобретает вакуумное ожидаемое значение, показывают значительные различия между случаями с учетом и без учета интерференций в зависимости от величины $aneta$ .

Исследование, представленное в статье, подчеркивает, что при поиске новой физики, особенно в столкновениях частиц, необходимо учитывать эффекты интерференции между сигналами от новых частиц и фоновыми процессами Стандартной модели. Игнорирование этих эффектов может привести к искажению наблюдаемых распределений и, как следствие, к ошибочным выводам. Это напоминает о важности критического подхода к анализу данных и признании ограниченности любой модели. Как писал Генри Дэвид Торо: «Не ищите убежища в общепринятых мнениях». Данная работа демонстрирует, что даже самые передовые методы анализа требуют постоянной проверки и сомнений, особенно когда речь идет о поиске явлений за пределами известных нам законов.

Что дальше?

Представленные результаты, как и любая попытка аппроксимировать реальность удобным способом, не претендуют на абсолютную истину. Напротив, они подчеркивают хрупкость выводов в поисках новой физики. Игнорирование интерференционных эффектов, пусть и оправданное упрощением расчетов, может привести к систематическим ошибкам, замаскированным под статистические флуктуации. Следует признать, что при анализе событий с ди-бозонами и ди-гиггсами, учет конечной ширины резонансов — это не просто техническая деталь, а фундаментальное требование для корректной интерпретации данных.

Дальнейшие исследования должны быть сосредоточены на разработке более точных методов моделирования интерференции, включая учет высших порядков в теории возмущений и эффектов, связанных с разбросом параметров новой физики. Необходимо помнить, что «сигнал» и «фон» — это не отдельные сущности, а переплетенные вероятности, и их разделение — это всегда некая степень приближения. И, конечно, стоит задуматься о разработке методов, позволяющих оценивать систематические ошибки, связанные с упрощением модели интерференции, чтобы, как минимум, понимать границы применимости полученных результатов.

В конечном счете, задача физики высоких энергий — не столько обнаружить новую физику, сколько научиться отличать правдоподобные объяснения от математических артефактов. Данные не лгут, но их интерпретация всегда несет на себе отпечаток человеческой предвзятости и ограниченности моделей.

Оригинал статьи: https://arxiv.org/pdf/2602.00256.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-03 11:28