Автор: Денис Аветисян
Новое исследование раскрывает, как аномалии в сильно неупорядоченных квантовых системах ограничивают поведение корреляционных функций, предсказывая характерные закономерности критического поведения.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
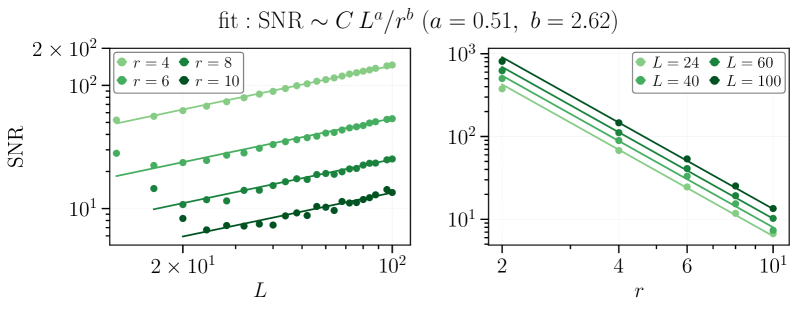
Бесплатный телеграм-канал![В исследовании случайной антиферромагнитной Гейзенберговской цепи демонстрируется степенной закон конечноразмерного масштабирования корреляционных функций для операторов, инвариантных относительно точных и усредненных симметрий (<span class="katex-eq" data-katex-display="false">\mathrm{CSSC}[Eq.8]</span> и <span class="katex-eq" data-katex-display="false">\mathrm{DfmD}[Eq.6]</span> соответственно), полученных с использованием метода сильной зависимости от беспорядка при <span class="katex-eq" data-katex-display="false">10^5</span> реализациях, при этом отображаются только данные с <span class="katex-eq" data-katex-display="false">r \geq 3</span> и <span class="katex-eq" data-katex-display="false">\mathrm{SNR} \geq 10</span>.](https://arxiv.org/html/2602.02648v1/x4.png)
Анализ аномалий в корреляционных функциях позволяет установить связь между случайными неоднородностями и критичностью в квантовых системах.
Квантовая критичность в сильно неупорядоченных системах представляет собой сложную задачу современной теории конденсированного состояния. В работе ‘Quantum criticality at strong randomness: a lesson from anomaly’ показано, что топология и аномалия, связанные со средней симметрией, позволяют предсказывать нетривиальные универсальные свойства. Ключевым результатом является вывод специфических законов распада корреляционных функций для локальных операторов, несущих заряд относительно точных или средних симметрий. Возможно ли использование этих аномалий для выявления ранее упущенных критических корреляций в хорошо изученных системах и разработки новых экспериментальных методов для их измерения?
Хрупкость Порядка: Введение в Сильное Беспорядочное Состояние
В большинстве теоретических моделей конденсированных сред предполагается идеальный порядок расположения атомов и молекул. Однако, реальные материалы, в отличие от этих упрощенных представлений, неизбежно содержат различные дефекты, примеси и случайные отклонения от совершенной структуры. Эти нарушения порядка, проявляющиеся в виде локальных искажений решетки, флуктуаций состава или случайных полей, оказывают существенное влияние на физические свойства вещества. Игнорирование этих факторов в теоретических расчетах может приводить к неверным предсказаниям и затруднять понимание наблюдаемых явлений. Таким образом, учет беспорядка является критически важным для адекватного описания поведения реальных материалов и разработки новых, функциональных материалов с заданными характеристиками.
В конденсированных средах, где случайные колебания преобладают над упорядоченностью — так называемое сильное беспорядочное состояние — традиционные теоретические подходы оказываются неэффективными. В отличие от систем с незначительными отклонениями от идеального порядка, в условиях сильного беспорядка флуктуации становятся доминирующими, что приводит к возникновению совершенно новых, экзотических фаз материи. Эти фазы характеризуются неожиданными свойствами, не наблюдаемыми в упорядоченных системах, и могут проявляться в виде нетривиальных магнитных состояний, необычной проводимости или даже совершенно новых типов сверхпроводимости. Исследование этих явлений требует разработки принципиально новых теоретических инструментов и экспериментальных методов, способных адекватно описать поведение материи в условиях, когда случайность определяет её свойства.
Понимание влияния сильного беспорядка имеет решающее значение для создания новых материалов с заданными свойствами, однако традиционные методы исследования зачастую оказываются неэффективными в таких условиях. Когда случайные колебания становятся доминирующими, стандартные теоретические подходы дают сбой, требуя разработки инновационных инструментов и методик анализа. Это включает в себя не только усовершенствование вычислительных моделей, способных учитывать хаотичность системы, но и создание экспериментальных установок, позволяющих исследовать материалы в условиях экстремального беспорядка. Именно преодоление этих сложностей открывает путь к конструированию материалов с уникальными характеристиками, например, сверхпроводимости при высоких температурах или необычными магнитными свойствами, которые невозможно получить в идеально упорядоченных системах.
За Пределами Простых Усреднений: Аномалии и Корреляции
В сильно неупорядоченных системах традиционные методы усреднения, такие как простое вычисление среднего значения по всем конфигурациям, часто приводят к возникновению “аномалий усреднения”. Это связано с тем, что усреднение скрывает важные физические явления, обусловленные флуктуациями, вызванными неупорядоченностью. Вместо того, чтобы получать репрезентативное значение, усреднение может давать результат, не отражающий истинное поведение системы. Эти аномалии возникают из-за того, что система испытывает различные локальные условия из-за случайного распределения параметров, и усреднение просто маскирует эти различия, приводя к неверной интерпретации результатов. Таким образом, для адекватного описания таких систем требуются более сложные методы, учитывающие влияние неупорядоченности.
Для адекватного описания систем с выраженной неупорядоченностью, недостаточно использовать усреднение по ансамблю состояний. Необходимо вычислять корреляционные функции, усредненные по ансамблю конфигураций случайного беспорядка. К таким функциям относятся, например, корреляция первого момента и коррелятор Эдвардса-Андерсона. Вычисление этих корреляций позволяет получить информацию о влиянии беспорядка на свойства системы, отражая не только средние значения, но и флуктуации, что дает более полное и точное представление о ее поведении, чем простое усреднение.
Корреляционные функции, такие как коррелятор Эдвардса-Андерсона (EA), позволяют более точно описать влияние беспорядка на свойства системы по сравнению с простым усреднением. В то время как усреднение может сгладить важные физические явления, корреляторы учитывают флуктуации, вызванные беспорядком, предоставляя детальную картину поведения системы. Коррелятор EA характеризуется убыванием по закону степеней с показателем -2, то есть r^{-2}, что указывает на характер корреляций между переменными в различных точках системы. Такой анализ позволяет выявить, как беспорядок влияет на локальные свойства и общую структуру системы, что невозможно сделать при использовании только средних значений.
![Анализ корреляционных функций в двумерной случайной решетке Майораны показал степенное масштабирование с размером системы, подтвержденное точной диагонализацией для коррелятора Эдвардса-Андерсона [Eq. 3] и коррелятора димеров первого момента [Eq. 6] при условии отношения сигнал/шум не менее 2 (для коррелятора Эдвардса-Андерсона) и 3 (для коррелятора димеров) при <span class="katex-eq" data-katex-display="false">r \geq 3</span>.](https://arxiv.org/html/2602.02648v1/x6.png)
Укрощение Беспорядка: Сильная Группа Перенормировки
Группа перенормировки при сильном беспорядке (SDRG) представляет собой эффективный возмущающий метод анализа систем с выраженным беспорядком. В отличие от стандартной теории возмущений, SDRG способна обрабатывать сильные корреляции, возникающие из-за случайного распределения параметров системы. Метод основан на последовательном исключении степеней свободы, не оказывающих существенного влияния на низкоэнергетическое поведение, что позволяет систематически отслеживать ренормировку параметров и выявлять доминирующие механизмы, определяющие свойства системы в пределе низких энергий. Эффективность SDRG подтверждена применением к различным моделям, включая модели Андерсона, спиновые стекла и системы с локализованными состояниями.
Метод сильной неупорядоченности ренормализационной группы (SDRG) последовательно исключает степени свободы системы, что позволяет эффективно проводить “грубое зерно” (coarse-graining). Этот процесс заключается в итеративном удалении высокоэнергетических степеней свободы, не оказывающих существенного влияния на низкоэнергетическое поведение системы. В результате, SDRG позволяет определить эффективную гамильтониану, описывающую систему на низких энергиях, и исследовать ее свойства, такие как критические явления и фазовые переходы, вызванные неупорядоченностью. Итеративное исключение степеней свободы позволяет систематически уменьшать размерность задачи, сохраняя при этом наиболее важные параметры, определяющие низкоэнергетическое поведение.
Метод сильной неупорядоченности ренормализационной группы (SDRG), часто реализуемый с использованием “трюка с репликами”, позволяет систематически исследовать влияние неупорядоченности на физические свойства системы. Данный подход заключается в последовательном устранении степеней свободы, что позволяет эффективно анализировать поведение системы при низких энергиях и выявлять возникающие фазы. “Трюк с репликами” — это математический метод, позволяющий усреднять по реализации случайных параметров, преобразуя задачу усреднения по ансамблю в задачу вычисления корреляционных функций для n реплик системы, где n стремится к нулю. Использование SDRG позволяет определить критические параметры, такие как критические температуры и экспоненты, характеризующие фазовые переходы в системах с сильным беспорядком.
Проявляющийся Порядок: Аномалии Симметрии и Топологические Фазы
В условиях сильного беспорядка в квантовых системах нередко возникают аномалии симметрии — ситуации, когда симметрии, присутствующие в классическом описании, оказываются нарушенными на квантовом уровне. Это происходит из-за флуктуаций, вызванных беспорядком, которые могут «подрывать» классические ограничения и приводить к новым, неожиданным состояниям материи. Например, даже незначительные отклонения от идеальной симметрии могут привести к спонтанному нарушению симметрии и появлению новых фаз с уникальными свойствами. Исследование этих аномалий симметрии открывает путь к пониманию новых типов квантовых состояний и позволяет предсказывать их поведение в экстремальных условиях, что имеет важное значение для развития квантовых технологий и материаловедения.
Аномалии симметрии, возникающие под влиянием сильного беспорядка, не являются произвольными, а подчиняются строгим ограничениям, известным как ограничение ЛСМ (LSM constraint). Это ограничение, по сути, диктует допустимые способы нарушения симметрии на квантовом уровне. Соблюдение этого ограничения может приводить к формированию новых, эмерджентных фаз материи, одной из наиболее ярких является случайная синглетная фаза (random singlet phase). В этой фазе спиновые моменты, вместо того чтобы упорядоченно выстраиваться, формируют случайные синглетные пары, что приводит к отсутствию дальнодействующего порядка и уникальным свойствам, отличающимся от традиционных магнитных состояний. Изучение этих фаз не только расширяет понимание фундаментальной физики конденсированного состояния, но и открывает перспективы для создания новых материалов с заданными свойствами.
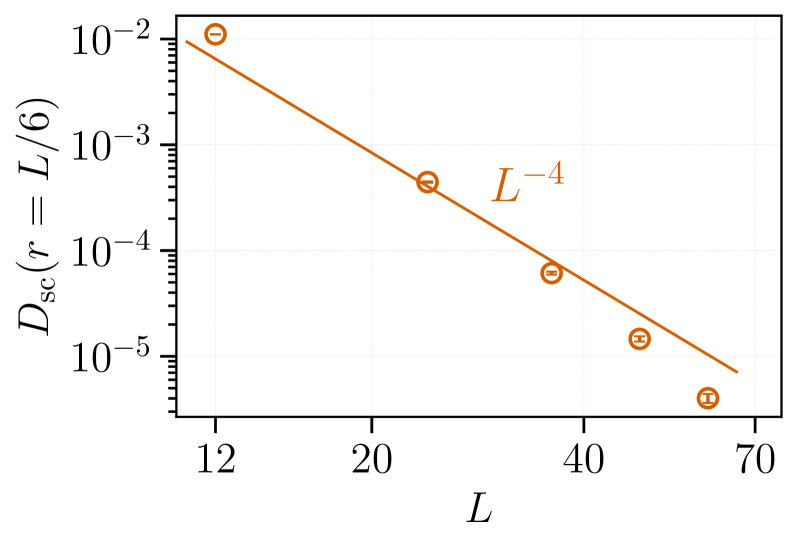
Беспорядок в квантовых системах способен приводить к возникновению фаз с топологическим порядком, отличающихся устойчивой вырожденностью основного состояния. Это явление представляет значительный интерес для квантовых вычислений, поскольку позволяет создавать устойчивые кубиты, защищенные от декогеренции. В таких фазах ключевую роль играют операторы, например, димерный оператор, корреляционная функция которого между димерами, связанных по образцу, затухает как r^{-4}, а функция первого момента корреляции димеров — как r^{-3}. Данные закономерности в поведении корреляционных функций являются характерным признаком топологического порядка и указывают на существование нелокальных степеней свободы, обеспечивающих устойчивость квантовой информации.
![Анализ корреляционных функций в случайных моделях Майорaны и антиферромагнитной Гейзенберга демонстрирует степенной закон зависимости от размера системы, подтверждаемый методами точной диагонализации и DMRG при различных параметрах случайности и пороговых значениях отношения сигнал/шум [SNR].](https://arxiv.org/html/2602.02648v1/x3.png)
Новый Подход: Беспорядок как Принцип Проектирования
Взаимодействие между беспорядком и квантовой механикой открывает захватывающие перспективы в разработке новых материалов. Традиционно, беспорядок рассматривался как нежелательное явление, снижающее эффективность материалов. Однако, современные исследования показывают, что контролируемый беспорядок может быть использован для настройки и оптимизации квантовых свойств, таких как проводимость и сверхпроводимость. В частности, введение определенных типов дефектов или случайных отклонений в кристаллическую структуру позволяет управлять движением электронов и создавать материалы с уникальными характеристиками, невозможными в идеально упорядоченных системах. Этот подход позволяет проектировать материалы с улучшенными оптическими, электронными и магнитными свойствами, открывая путь к созданию инновационных устройств и технологий, например, более эффективных солнечных батарей или квантовых компьютеров. Исследования в этой области демонстрируют, что осознанное использование беспорядка — это не просто преодоление ограничений, а активный инструмент для создания материалов будущего.
Модель «свободного фермиона», подвергающаяся воздействию беспорядка, представляет собой уникальную платформу для проверки и развития новых теоретических подходов в физике. Введение дефектов и случайных потенциалов в эту упрощенную систему позволяет исследовать, как беспорядок влияет на ключевые квантово-механические свойства, такие как локализация и транспорт электронов. Анализ поведения фермионов в условиях беспорядка помогает уточнить существующие теории, например, теорию Андерсона, и разработать более точные модели для описания реальных материалов. Исследования в данной области не только углубляют понимание фундаментальных физических явлений, но и создают основу для предсказания и конструирования материалов с заданными свойствами, например, сверхпроводников или топологических изоляторов. Изучение влияния беспорядка на \psi(x) -волновую функцию фермиона — позволяет выявить новые физические механизмы и расширить границы применимости существующих теоретических инструментов.
В настоящее время активно исследуется возможность использования неупорядоченности не как помехи, а как принципиально нового подхода к созданию материалов с уникальными свойствами. Вместо стремления к идеальной кристаллической решетке, ученые обращают внимание на системы, в которых присутствует контролируемый хаос на атомном уровне. Этот подход позволяет создавать материалы, демонстрирующие неожиданные электронные, оптические и механические характеристики, недостижимые в традиционных упорядоченных структурах. Например, введение дефектов или случайных примесей может привести к возникновению новых квантовых состояний и улучшению проводимости, что открывает перспективы для разработки сверхпроводников нового поколения, высокоэффективных солнечных батарей и материалов с программируемыми свойствами. Подобный подход требует переосмысления фундаментальных принципов материаловедения и разработки новых теоретических моделей, способных предсказывать и контролировать поведение неупорядоченных систем.
Исследование, представленное в статье, демонстрирует, как аномалии в беспорядочных квантовых системах накладывают ограничения на корреляционные функции, предсказывая специфические степенные зависимости для операторов с зарядом симметрии. Этот подход напоминает философские взгляды Джона Локка, который утверждал: «Знание начинается с ощущений». Подобно тому, как Локк видел в чувственном опыте основу познания, данное исследование опирается на детальный анализ корреляционных функций — своеобразных «чувственных данных» квантовой системы — для понимания критического поведения. Установление связи между аномалиями и степенными законами в корреляциях позволяет выявить фундаментальные принципы, определяющие структуру и поведение этих систем, подобно тому, как структура определяет поведение, что соответствует основным принципам, изложенным в статье.
Что впереди?
Представленная работа, демонстрируя влияние аномалий на корреляционные функции в сильно разупорядоченных квантовых системах, скорее открывает ящик Пандоры, нежели закрывает вопрос о квантовой критичности. Представленный подход, подобно грамотному проектированию городской инфраструктуры, позволяет предсказывать поведение системы, избегая необходимости её полной перестройки при малейших изменениях. Однако, понимание границ применимости этих предсказаний остаётся нерешенной задачей. В частности, остается открытым вопрос о том, как предложенный механизм взаимодействует с другими формами разупорядоченности, не охваченными данной моделью.
Настоящая работа подчеркивает важность понимания структуры, определяющей поведение системы. Дальнейшие исследования должны быть направлены на разработку более общих методов, позволяющих выявлять и характеризовать аномалии в различных квантовых системах. Потребуется более глубокое изучение влияния топологии и размерности на критическое поведение. Элегантность решения часто кроется в простоте, но игнорирование нюансов может привести к неожиданным последствиям.
В конечном счете, задача состоит не в том, чтобы найти единственное правильное описание квантовой критичности, а в том, чтобы создать гибкую и адаптивную систему знаний, способную объяснить разнообразие наблюдаемых явлений. Именно такой подход позволит избежать упрощенных моделей, не отражающих всей сложности реального мира.
Оригинал статьи: https://arxiv.org/pdf/2602.02648.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Все рецепты культистского круга в Escape from Tarkov
- Нечестивцам нет покоя: как получить старый ключ от коттеджа
- Решение головоломки с паролем Absolum в Yeldrim.
- Arknights: Endfield — Интерактивная карта (Долина IV)
- Акции UGLD. Южуралзолото ГК: прогноз акций.
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- В ролях: приглашенные звезды и актеры 22-го сезона 3-й серии «Морской полиции» (фотографии) – Донна Миллс в беде с Хэлом
- Где найти руду Ферриума в Arknights Endfield
2026-02-04 15:51