Геометрия магнетизма: новый взгляд на квантовые материалы

Автор: Денис Аветисян

Исследование выявило нелинейный орбитальный магнетизм в квантовых материалах, обусловленный геометрическими свойствами импульсного пространства.

В рамках общей теории относительности Эйнштейна, нелинейная намагниченность, возникающая в ответ на электрическое поле, описывается квантовым символом Кристоффеля в импульсном пространстве, что указывает на то, что электрическое поле не только индуцирует искривление квантового пространства, но и способствует возникновению «петлевого тока» орбитального движения электронов, приводящего к намагниченности, квадратичной относительно напряженности поля.

Открыт нелинейный орбитальный магнетизм, описываемый квантовым символом Кристоффеля, независимым от спин-орбитального взаимодействия.

Несмотря на устоявшиеся представления о роли спин-орбитального взаимодействия в возникновении магнитных свойств материалов, в настоящей работе, посвященной ‘Quantum Christoffel Nonlinear Magnetization’, обнаружена новая форма нелинейной орбитальной намагниченности. Эта намагниченность описывается квантовым символом Кристоффеля, возникающим из геометрических свойств импульсного пространства и не требующим наличия спин-орбитального взаимодействия или нарушения инверсионной симметрии. В частности, показано, что такие материалы, как BiF$_3$, ZnI$_2$ и Ru$_4$Se$_5$, являются перспективными кандидатами для проявления данного эффекта, а сам символ Кристоффеля может быть исследован с помощью оптоэлектронных и транспортных методов. Не открывает ли это новое понимание фундаментальной связи между геометрией и физикой в квантовых материалах?

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Геометрическая Основа Пространства-Времени и Квантовых Состояний

В основе понимания гравитации, как её описывает общая теория относительности Эйнштейна, лежит представление о геометрических свойствах пространства-времени. Вместо силы, действующей на расстоянии, гравитация рассматривается как искривление геометрии, вызванное наличием массы и энергии. Ключевым инструментом для описания этого искривления является символ Кристоффеля $\Gamma^{\mu}_{\nu \lambda}$ , определяющий, как изменяются координаты при перемещении в искривлённом пространстве. Этот символ, являясь частью тензора Римана, позволяет математически точно описывать геометрию пространства-времени и, следовательно, предсказывать поведение объектов под воздействием гравитации. Именно геометрическое описание, а не представление о гравитации как о силе, позволило Эйнштейну совершить революцию в нашем понимании Вселенной, предсказав такие явления, как гравитационное линзирование и существование чёрных дыр.

В рамках расширения геометрического подхода к квантовой механике, понятие квантовой метрики определяет “расстояние” между различными квантовыми состояниями. Эта метрика, отличная от привычного евклидова расстояния, позволяет измерить степень различия между состояниями, учитывая их вероятностную природу и суперпозицию. $g_{ij}$ — тензор квантовой метрики, определяющий эту “геометрию” квантового пространства состояний. Изучение квантовой метрики позволяет предположить, что пространство квантовых состояний обладает собственной геометрией, не обязательно совпадающей с геометрией пространства-времени, но потенциально связанной с ней. Подобное отождествление открывает перспективные пути для объединения общей теории относительности и квантовой механики, предполагая, что гравитация и квантовые явления могут быть проявлениями единой, более фундаментальной геометрической структуры.

Орбитальная Магнетизация и Кривизна Берри: Возникающие Квантовые Свойства

Орбитальная намагниченность, описывающая движение электронов по орбиталям, тесно связана с кривизной Берри — геометрическим свойством, влияющим на квантовое поведение. Кривизна Берри возникает из-за фазовых изменений волновой функции электрона в импульсном пространстве и проявляется как эффективное магнитное поле, действующее на электрон, даже в отсутствие внешнего магнитного поля. Математически, орбитальная намагниченность $\mathbf{M}$ связана с кривизной Берри $\mathbf{\Omega}$ через выражение $\mathbf{M} \propto \nabla \times \mathbf{\Omega}$ . Таким образом, кривизна Берри определяет вклад орбитального момента в общую намагниченность материала, что существенно влияет на его электронные и транспортные свойства.

Для расчета и анализа квантовомеханических свойств, таких как орбитальная намагниченность и кривизна Берри, используются различные методы. Динамика волновых пакетов позволяет непосредственно моделировать эволюцию квантовых состояний во времени и вычислять соответствующие наблюдаемые. Уравнение Больцмана, применяемое в полуклассическом приближении, описывает транспорт электронов и позволяет оценить влияние кривизны Берри на кинетические свойства материалов, включая аномальный эффект Холла. Численное решение этих уравнений, с использованием современных вычислительных методов, дает возможность предсказывать и интерпретировать экспериментальные результаты, связанные с этими квантовыми явлениями. $\mathbf{E} = -\nabla V - \frac{d\mathbf{A}}{dt}$

Квантовый аномальный эффект Холла (Quantum Anomalous Hall Effect, QAHE) представляет собой фазу материи, характеризующуюся квантованной проводимостью $e^2/h$ без применения внешнего магнитного поля. Данное явление обусловлено ненулевой кривизной Берри в электронной структуре материала, приводящей к появлению эффективного магнитного поля в импульсном пространстве. Это позволяет электронам двигаться по краю образца без рассеяния, даже в отсутствие внешнего поля, что приводит к диссипативной проводимости, квантованной в единицах $e^2/h$ . Реализация QAHE требует определенных свойств электронной структуры, таких как наличие ненулевого топологического инварианта, и наблюдалась в различных материалах, включая легированные двумерные электронные газы и материалы типа Heusler.

Первопринципные расчеты показали, что двумерный BiF3 обладает выраженной нелинейной восприимчивостью к магнитному моменту <span class="katex-eq" data-katex-display="false"> \alpha_{zxx} </span>, зависящей от энергии Ферми и обусловленной в основном квантовым символом Кристоффеля, что проявляется в эффекте Керра и вращении плоскости поляризации света. — Первопринципные расчеты показали, что двумерный BiF3 обладает выраженной нелинейной восприимчивостью к магнитному моменту $\alpha_{zxx}$ , зависящей от энергии Ферми и обусловленной в основном квантовым символом Кристоффеля, что проявляется в эффекте Керра и вращении плоскости поляризации света.

Нелинейный Отклик и Квантовый Символ Кристоффеля

Нелинейная орбитальная намагниченность представляет собой отклонение от линейного отклика материала на приложенное электрическое поле. В традиционных материалах, намагниченность пропорциональна напряженности электрического поля $\mathbf{E}$ . Однако, в некоторых системах наблюдается, что намагниченность изменяется нелинейно, то есть, зависимость между намагниченностью $\mathbf{M}$ и электрическим полем описывается нелинейной функцией $\mathbf{M} = f(\mathbf{E})$ , где $f$ не является линейной функцией. Данное явление обусловлено сложными взаимодействиями между электронами в материале и проявляется при достаточно сильных электрических полях, когда линейная аппроксимация становится недействительной.

Квантовый символ Кристоффеля выступает ключевым дескриптором нелинейного поведения, связывая орбитальную намагниченность и электрические поля в геометрическом формализме. В рамках проведенных исследований установлено, что вклад данного символа значительно превосходит вклад не-Кристоффелевских членов в описываемую нелинейную связь. Это позволяет рассматривать его как доминирующий фактор, определяющий нелинейный отклик системы на внешние электрические воздействия и обеспечивающий основу для геометрического описания данного явления. $\Gamma_{ijk}$ представляет собой тензор, характеризующий связь между координатами и их производными, и в данном контексте отражает влияние электрического поля на орбитальный магнитный момент.

Соблюдение симметрии частица-дырка и наличие дираковских фермионов создают основу для управления квантовыми транспортными явлениями. В системах, удовлетворяющих этим требованиям, нелинейный отклик на электрические поля, описываемый квантовым символом Кристоффеля, позволяет контролировать орбитальную намагниченность и, как следствие, изменять характеристики квантового транспорта. Это достигается за счет возможности манипулирования геометрией электронных состояний и управления потоком носителей заряда, что открывает перспективы для разработки новых типов квантовых устройств и материалов с заданными транспортными свойствами. $\text{Например, управление спиновым током или создание топологически защищенных состояний.}$

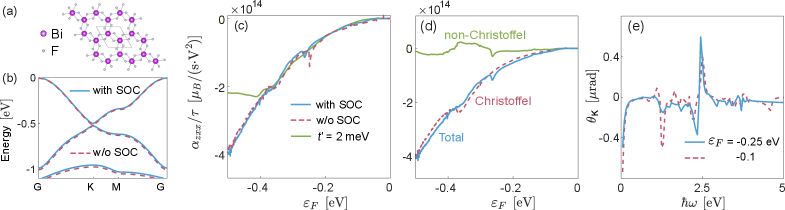
Анализ нелинейного коэффициента намагниченности <span class="katex-eq" data-katex-display="false">\alpha_{zxx}</span> для эффективной модели [Eq. (B1)] показывает его зависимость от энергии Ферми и параметра нарушения симметрии частиц и дырок, при этом нарушение симметрий вращения и отражения влияет на величину этого коэффициента, что подтверждается сравнением зонной структуры при наличии и отсутствии симметрии частиц и дырок. — Анализ нелинейного коэффициента намагниченности $\alpha_{zxx}$ для эффективной модели [Eq. (B1)] показывает его зависимость от энергии Ферми и параметра нарушения симметрии частиц и дырок, при этом нарушение симметрий вращения и отражения влияет на величину этого коэффициента, что подтверждается сравнением зонной структуры при наличии и отсутствии симметрии частиц и дырок.

Материальная Реализация и Экспериментальная Верификация

Бифторид висмута (BiF₃) представляет собой перспективную материальную систему для исследования нелинейного орбитального магнетизма благодаря своей специфической электронной структуре. В BiF₃ наблюдается сильное спин-орбитальное взаимодействие и узкие полосы, что приводит к значительному влиянию орбитального момента на магнитные свойства. Электронная конфигурация Bi³⁺, характеризующаяся заполненной d-оболочкой, способствует формированию локализованных орбитальных моментов, которые могут быть когерентно возбуждены внешним магнитным полем. Сочетание этих факторов делает BiF₃ подходящим материалом для изучения механизмов нелинейного ответа, связанных с орбитальным магнетизмом, и проверки теоретических моделей, предсказывающих подобные явления.

Теория функционала плотности (DFT) и функции Ванье являются ключевыми вычислительными инструментами для характеристики BiF₃ и прогнозирования его отклика на внешние воздействия. DFT позволяет рассчитать электронную структуру материала, включая распределение заряда и энергии, что необходимо для понимания его физических свойств. Функции Ванье, в свою очередь, служат для построения локализованных орбиталей, описывающих поведение электронов в кристаллической решетке BiF₃. Комбинация этих методов позволяет моделировать нелинейные оптические свойства материала, предсказывая, например, величину и поляризацию эффекта Керра, а также анализировать вклад различных электронных состояний в наблюдаемый отклик. Точность предсказаний, полученных с использованием DFT и функций Ванье, критически важна для интерпретации экспериментальных данных и подтверждения теоретических моделей.

Наблюдение эффекта Керра является ключевым экспериментальным подтверждением предсказанной нелинейной магнитной восприимчивости BiF₃ и валидацией теоретической модели, основанной на расчетах с использованием теории функционала плотности и функций Ванье. Теоретические оценки показывают, что угол поворота плоскости поляризации в эффекте Керра составит порядка микрорадиан (μrad), что находится в пределах досягаемости современных экспериментальных установок и позволяет провести количественное сравнение с результатами расчетов. Обнаружение этого эффекта станет прямым доказательством нелинейных магнитных свойств материала.

Влияние на Квантовые Технологии и Перспективы Дальнейших Исследований

Геометрический контроль квантовых состояний посредством нелинейной намагниченности открывает перспективные возможности для развития спинтроники и квантовых вычислений. В основе этого подхода лежит возможность манипулирования спином электронов не за счет традиционных магнитных полей, а путем изменения геометрии намагниченности материала. Это позволяет создавать более компактные и энергоэффективные устройства для обработки и хранения квантовой информации. В частности, контролируемое изменение направления намагниченности позволяет точно управлять спиновыми кубитами, что критически важно для реализации квантовых алгоритмов. Потенциальные применения охватывают разработку новых типов квантовых датчиков, запоминающих устройств и логических элементов, превосходящих по характеристикам существующие аналоги. Исследования в этой области направлены на создание материалов с высокой нелинейностью намагниченности и способностью поддерживать когерентность квантовых состояний в течение длительного времени.

Исследование материалов, демонстрирующих сверхпроводимость в плоской зоне и поведение дробного квантового эффекта Холла, представляет собой перспективное направление для усиления возможностей геометрического управления квантовыми состояниями. В этих материалах, благодаря уникальным электронным свойствам, возникает повышенная чувствительность к внешним воздействиям, что позволяет более эффективно манипулировать спиновыми состояниями и, как следствие, повышать точность и надежность квантовых вычислений и спинтронных устройств. Ожидается, что использование подобных материалов позволит добиться более выраженного нелинейного эффекта намагниченности, открывая новые горизонты для создания компактных и энергоэффективных квантовых технологий. $E(k) = \frac{\hbar^2 k^2}{2m}$ Подобные материалы предоставляют платформу для реализации более сложных квантовых схем и алгоритмов, что крайне важно для развития квантовой информатики.

Предложенный подход к управлению квантовыми состояниями посредством нелинейной намагниченности знаменует собой существенный сдвиг в парадигме понимания и манипулирования квантовыми явлениями. Оценка величины нелинейной намагниченности, достигающая $10^{-4} \mu_B$ , указывает на потенциально значительный эффект, способный открыть новые пути для технологических инноваций. Это позволяет предположить возможность создания принципиально новых устройств для спинтроники и квантовой обработки информации, основанных на более эффективном и точном контроле над квантовыми битами. Перспективы использования данного подхода простираются за рамки существующих технологий, предлагая возможности для разработки материалов и устройств с улучшенными характеристиками и функциональностью.

Данная работа демонстрирует изящество и глубину понимания взаимосвязи между геометрией и физическими свойствами материалов. Исследование нелинейной орбитальной намагниченности, описываемой квантовым символом Кристоффеля, раскрывает новые грани топологических материалов. Подобно тому, как хорошо спроектированная архитектура незаметна в своей функциональности, данное открытие проявляется в фундаментальных свойствах импульсного пространства, независимых от спин-орбитального взаимодействия. Как заметил Галилей Галилей: «Вселенная — это книга, написанная на языке математики». И в данном исследовании, математический язык раскрывает скрытые закономерности, элегантно описывающие поведение квантовых систем.

Куда же это ведёт?

Обнаруженная связь между геометрией импульсного пространства и нелинейной орбитальной намагниченностью, выраженная через квантовый символ Кристоффеля, открывает, скорее, вопросы, чем даёт ответы. Элегантность этого подхода — в независимости от спин-орбитального взаимодействия — предполагает, что фундаментальные принципы геометрической фазы могут быть гораздо более всеобъемлющими, чем считалось ранее. Однако, остаётся неясным, как эта геометрическая намагниченность проявляется в реальных материалах, особенно в присутствии беспорядка и несовершенств. Простое существование недостаточно; необходимо понимать, как её контролировать и использовать.

Очевидным следующим шагом представляется поиск материалов, в которых этот эффект наиболее выражен и легко обнаружим. Но, пожалуй, более сложной задачей является разработка теории, способной предсказать и объяснить влияние этой геометрической намагниченности на другие физические свойства — теплопроводность, оптические свойства, и даже сверхпроводимость. Иначе говоря, необходимо выйти за рамки простого описания и перейти к предсказанию.

Возможно, самое интересное — это перспектива использования этой геометрической намагниченности для создания новых типов устройств, основанных на управлении топологическими свойствами материалов. Но прежде, необходимо признать, что большинство современных концепций управления спином — это, по сути, грубые приближения. Истинное управление — это не манипуляция, а гармония с фундаментальными принципами.

Оригинал статьи: https://arxiv.org/pdf/2602.03597.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-05 00:12