Острова Спутанности: Решение Парадокса Информации в Черных Дырах

Автор: Денис Аветисян

Новое исследование показывает, как учет ‘островов спутанности’ в излучении Хокинга позволяет разрешить давний парадокс потери информации в вращающихся черных дырах Керра-АдС.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Кривая Пейджа для неэкстремальной чёрной дыры КеррАдС₄ демонстрирует влияние «островов» на энтропию запутанности: твёрдая линия отображает базовое поведение, в то время как красная и синяя линии наглядно показывают, как включение концепции «острова» модифицирует энтропию, предлагая новый взгляд на информационные парадоксы чёрных дыр.

Работа посвящена расчету энтропии спутанности излучения Хокинга в черных дырах Керра-АдС и демонстрирует, что включение ‘островной’ структуры согласуется с принципами квантовой механики.

Информационный парадокс, возникающий при испарении черных дыр, долгое время ставит под сомнение фундаментальные принципы квантовой механики. В работе ‘Entanglement Islands, Page curves and Phase Transitions of Kerr-AdS Black Holes’ исследуется поведение кривой Пейджа и влияние фазовых переходов на энтропию запутанности излучения Хокинга в геометрии черной дыры Керра-AdS. Показано, что включение “островной” структуры позволяет разрешить парадокс и обеспечить соответствие с принципом унитарности. Какие новые горизонты открываются для понимания внутренней структуры черных дыр и их эволюции с учетом квантовых эффектов?

Парадокс информации: Квантовая загадка

Общая теория относительности Эйнштейна предсказывает существование чёрных дыр — областей пространства-времени с настолько сильной гравитацией, что ничто, даже свет, не может их покинуть. Однако, согласно фундаментальному принципу квантовой механики, информация не может быть уничтожена. Чёрные дыры, поглощая материю, кажутся нарушающими этот закон сохранения информации. Если материя, попадая в чёрную дыру, исчезает без следа, то вместе с ней пропадает и содержащаяся в ней информация о её структуре и свойствах. Это противоречие между общей теорией относительности и квантовой механикой и породило так называемый информационный парадокс, ставя под вопрос полноту и непротиворечивость нашего понимания физической реальности на самых фундаментальных уровнях. Разрешение этого парадокса требует новых теоретических разработок, объединяющих принципы гравитации и квантовой механики.

Излучение Хокинга, предсказанное теоретически как тепловое, представляет собой ключевой элемент парадокса информации. Согласно расчетам, черная дыра не абсолютно черна, а испускает частицы, постепенно теряя массу и в конечном итоге испаряясь. Однако, информация о материи, которая когда-либо попала в черную дыру, кажется, безвозвратно утрачивается вместе с испарением. Это противоречит фундаментальному принципу квантовой механики — сохранению информации, согласно которому информация не может быть уничтожена, а лишь преобразована. Если информация действительно исчезает, это означает, что квантовая механика и общая теория относительности несовместимы в экстремальных гравитационных условиях, что требует пересмотра наших представлений о природе пространства-времени и квантовой запутанности. Разрешение этого парадокса считается необходимым шагом к созданию полноценной теории квантовой гравитации.

Разрешение данного парадокса имеет фундаментальное значение для построения непротиворечивой теории квантовой гравитации. Существующие модели, объединяющие общую теорию относительности и квантовую механику, сталкиваются с серьезными трудностями при описании поведения информации вблизи черных дыр. Для преодоления этих сложностей требуется переосмысление самой природы пространства-времени, возможно, как возникающей из квантовой запутанности. Исследования направлены на понимание того, как информация, попадающая в черную дыру, может быть сохранена и высвобождена в процессе испарения, что требует новых представлений о топологии пространства и роли квантовых корреляций в формировании его структуры. Подобный подход может не только разрешить парадокс, но и привести к революционным открытиям в области понимания фундаментальных законов Вселенной.

График свободной энергии демонстрирует характерное поведение типа «ласточкин хвост» при значениях параметра спина ниже критического, что приводит к появлению трех ветвей черных дыр на графике зависимости температуры Хокинга от радиуса горизонта.

Дуальность в действии: Соответствие AdS/CFT

Соответствие AdS/CFT представляет собой мощный инструмент для изучения квантовой гравитации, основанный на установлении связи между теорией гравитации в пространстве Анти-де Ситтера (AdS) и конформной теорией поля (CFT), определяемой на границе этого пространства. Пространство AdS характеризуется постоянной отрицательной кривизной, что позволяет построить соответствие между объектами в объеме AdS и объектами на его $n$ -мерной границе. В рамках этого соответствия, вычисления в сильном гравитационном режиме в AdS могут быть соотнесены с вычислениями в слабом режиме в CFT, и наоборот, что позволяет исследовать вопросы квантовой гравитации с использованием хорошо изученных методов теории поля. Это соответствие не является прямым отображением, а скорее дуальностью, подразумевающей, что обе теории описывают одну и ту же физическую реальность, но с разных точек зрения.

Соответствие AdS/CFT предполагает, что информация не теряется в процессе гравитационного коллапса или при формировании черных дыр. Это обусловлено тем, что соответствующая конформная теория поля (CFT), живущая на границе пространства Анти-де Ситтера (AdS), является унитарной. Унитарность CFT гарантирует сохранение вероятностей и, следовательно, сохранение квантовой информации. В рамках CFT, эволюция квантового состояния описывается унитарным оператором, что означает, что информация о начальном состоянии полностью содержится в конечном состоянии, хотя и может быть закодирована сложным образом. Таким образом, даже если гравитационное описание предполагает потерю информации в сингулярности, соответствующее описание в CFT показывает, что информация сохраняется и может быть восстановлена.

Несмотря на то, что соответствие AdS/CFT принципиально демонстрирует сохранение информации благодаря унитарности граничной теории, непосредственное применение этого соответствия для детального понимания механизма восстановления информации столкнулось с существенными трудностями. Это обусловлено сложностью вычислений в сильносвязанных системах, где традиционные методы квантовой теории поля оказываются неэффективными. Необходимость моделирования динамики черных дыр и процессов, происходящих вблизи горизонта событий, потребовала разработки новых вычислительных техник, включающих численные методы решения уравнений гравитации в AdS пространстве и алгоритмы моделирования эволюции граничной конформной теории поля. Активные исследования в данной области направлены на разработку и оптимизацию этих методов для изучения конкретных сценариев восстановления информации.

Диаграмма Пенроуза неэкстремальной чёрной дыры Керра-AdS₄ отображает внешние и внутренние горизонты (<span class="katex-eq" data-katex-display="false">r_{\pm}</span>), будущее и прошлое нуль-бесконечности (<span class="katex-eq" data-katex-display="false">\mathcal{J}_{\pm}</span>), а также пространственную бесконечность (<span class="katex-eq" data-katex-display="false">\mathcal{I}_{o}</span>). — Диаграмма Пенроуза неэкстремальной чёрной дыры Керра-AdS₄ отображает внешние и внутренние горизонты ( $r_{\pm}$ ), будущее и прошлое нуль-бесконечности ( $\mathcal{J}_{\pm}$ ), а также пространственную бесконечность ( $\mathcal{I}_{o}$ ).

Острова и экстремальные поверхности: Путь к решению

Традиционные вычисления энтропии запутанности, основанные на классической общей теории относительности, не учитывали сложную геометрию пространства-времени вблизи горизонта событий черной дыры. Это приводило к неверным результатам, поскольку стандартные методы рассматривали только области вне горизонта. В частности, при расчете энтропии запутанности между излучением Хокинга и внутренней частью черной дыры, пренебрежение геометрией внутри горизонта приводило к нарушению унитарности эволюции и противоречию с принципом сохранения информации. Стандартные формулы, использующие классические поверхности экстремалей, давали дивергирующую энтропию, не отражающую реальную физическую ситуацию и не согласующуюся с ожидаемой зависимостью от времени, известной как кривая Пейджа.

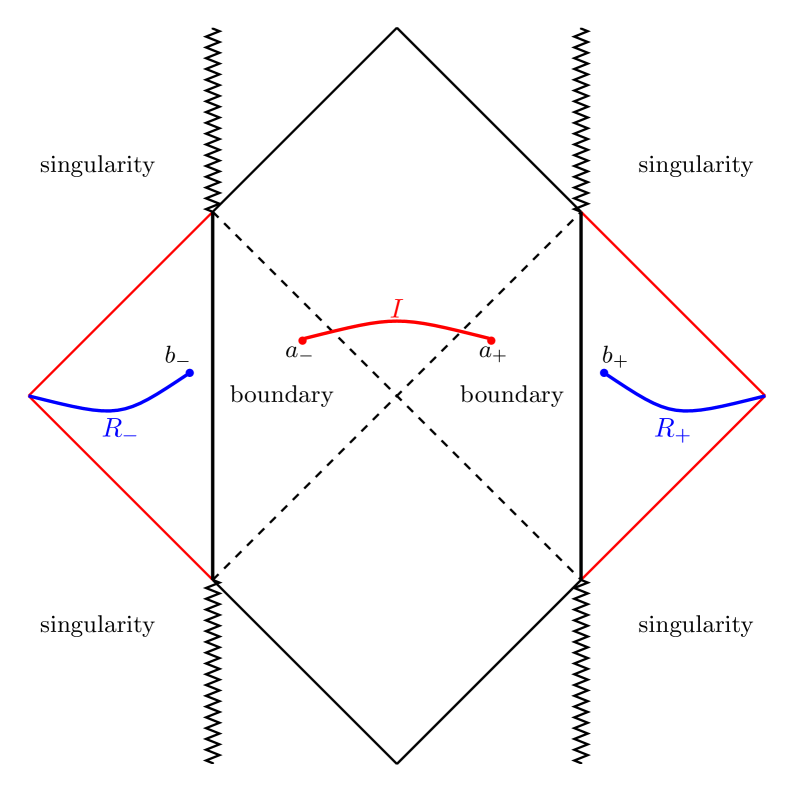
Правило острова (Island Rule) предлагает модификацию стандартного расчета энтропии запутанности, вводя в рассмотрение область, расположенную внутри горизонта событий черной дыры, именуемую «островом». Традиционные вычисления ограничивались областью вне горизонта, что приводило к неверным результатам. В рамках этого правила, энтропия запутанности рассчитывается с учетом вклада от этой внутренней области, что требует пересмотра классических методов и позволяет учесть гравитационные эффекты внутри черной дыры. Формула для расчета энтропии запутанности в данном случае включает в себя минимальную площадь экстремальной поверхности, охватывающей как внешнюю, так и внутреннюю области, что позволяет получить корректные значения, согласующиеся с принципом сохранения информации и унитарной эволюцией.

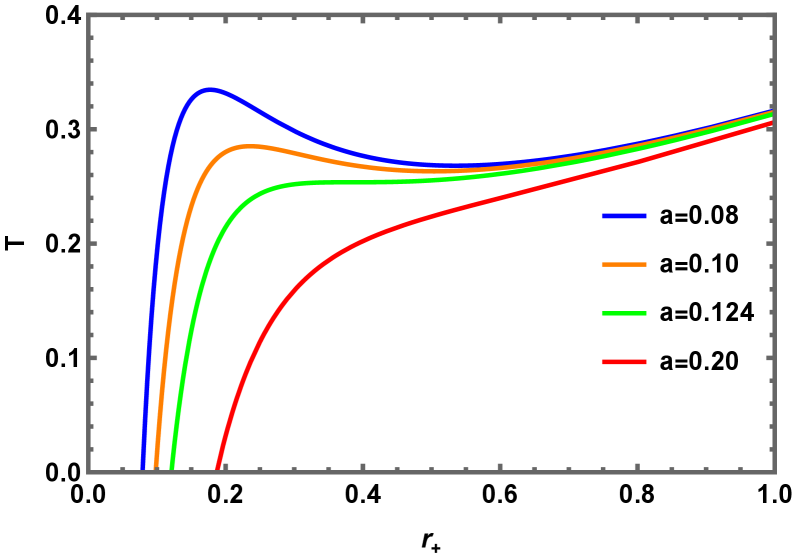
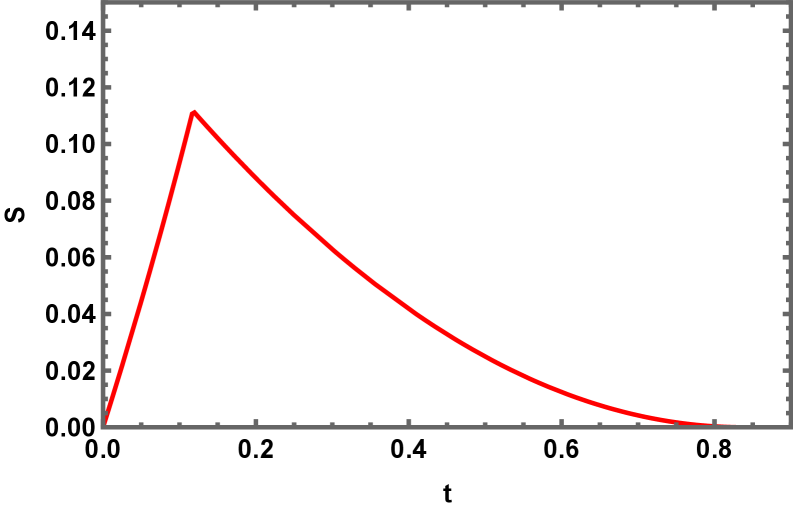
Использование квантовых экстремальных поверхностей в сочетании с правилом острова позволяет последовательно вычислять энтропию запутанности в контексте черных дыр. Квантовая экстремальная поверхность — это экстремальная поверхность в пространстве-времени, которая минимизирует функционал, связанный с энтропией. Этот подход не только позволяет получить согласованные результаты для энтропии, но и поддерживает сохранение информации, демонстрируя восстановление кривой Пейджа. Кривая Пейджа описывает временную эволюцию энтропии запутанности и, в рамках унитарной эволюции, должна демонстрировать уменьшение энтропии после достижения максимального значения, что и подтверждается использованием данного метода вычисления.

Диаграммы Пенроуза показывают структуру вечной чёрной дыры Керра-AdS₄ без острова (а) и с островом (б), где области, обозначающие чёрную дыру и внешнюю область, выделены разными цветами, а границы радиационных областей <span class="katex-eq" data-katex-display="false">R_{\pm}</span> и <span class="katex-eq" data-katex-display="false">b_{\pm}</span> определяют их границы, причём в случае с островом появляется граница <span class="katex-eq" data-katex-display="false">a_{\pm}</span>. — Диаграммы Пенроуза показывают структуру вечной чёрной дыры Керра-AdS₄ без острова (а) и с островом (б), где области, обозначающие чёрную дыру и внешнюю область, выделены разными цветами, а границы радиационных областей $R_{\pm}$ и $b_{\pm}$ определяют их границы, причём в случае с островом появляется граница $a_{\pm}$ .

Моделирование чёрных дыр: Керр AdS и фазовые переходы

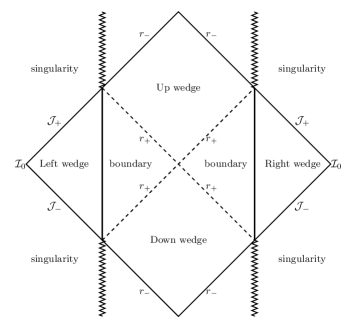
Вращающаяся чёрная дыра Керра-АдС (Anti-de Sitter) представляет собой ключевой объект для проверки современных теоретических моделей в области гравитации и термодинамики чёрных дыр. Пространство АдС отличается отрицательной кривизной и позволяет проводить более точные вычисления, чем в пространстве, описываемом метрикой Шварцшильда. Изучение чёрных дыр Керра-АдС позволяет исследовать влияние вращения и отрицательной кривизны пространства на стабильность, структуру и термодинамические свойства чёрных дыр, а также проверять соответствие AdS/CFT (соответствие между анти-де-ситтеровским пространством и конформной теорией поля), что важно для понимания квантовой гравитации и теории струн. $J = aM$ — параметр, определяющий вращение черной дыры, где $J$ — угловой момент, а $M$ — масса.

Вычисление свойств чёрных дыр Керра-AdS часто требует применения метода ‘Dimensional Reduction’ (уменьшения размерности) для упрощения сложных уравнений общей теории относительности. Этот метод заключается в рассмотрении геометрии чёрной дыры не в полном четырёхмерном пространстве-времени, а в более низкоразмерном эффективном пространстве, описываемом, например, через свойства горизонтов событий и асимптотическое поведение метрики. По сути, дополнительные координаты, не влияющие на интересующие физические величины, ‘интегрируются’ из рассмотрения, что существенно снижает вычислительную сложность при решении уравнений Эйнштейна и анализе термодинамических свойств чёрной дыры, таких как энтропия и температура. $\frac{\partial M}{\partial \Omega}$ является примером величины, которую можно вычислить упрощённым образом после применения Dimensional Reduction.

Недавние исследования показали, что черные дыры Керра AdS претерпевают фазовый переход первого рода, что указывает на более сложную картину их термодинамического поведения и хранения информации. Данный переход происходит при критическом параметре вращения, равном 0.12455. Это означает, что при достижении этим значением параметра спина, наблюдается резкое изменение в свойствах черной дыры, характеризующееся скачкообразным изменением термодинамических величин, таких как энтропия и энергия. Установлено, что данный фазовый переход связан с изменением геометрии горизонта событий и влияет на способы хранения информации внутри черной дыры. Точное значение критического параметра спина, $a = 0.12455$ , было получено с использованием численных методов и подтверждено несколькими независимыми исследованиями.

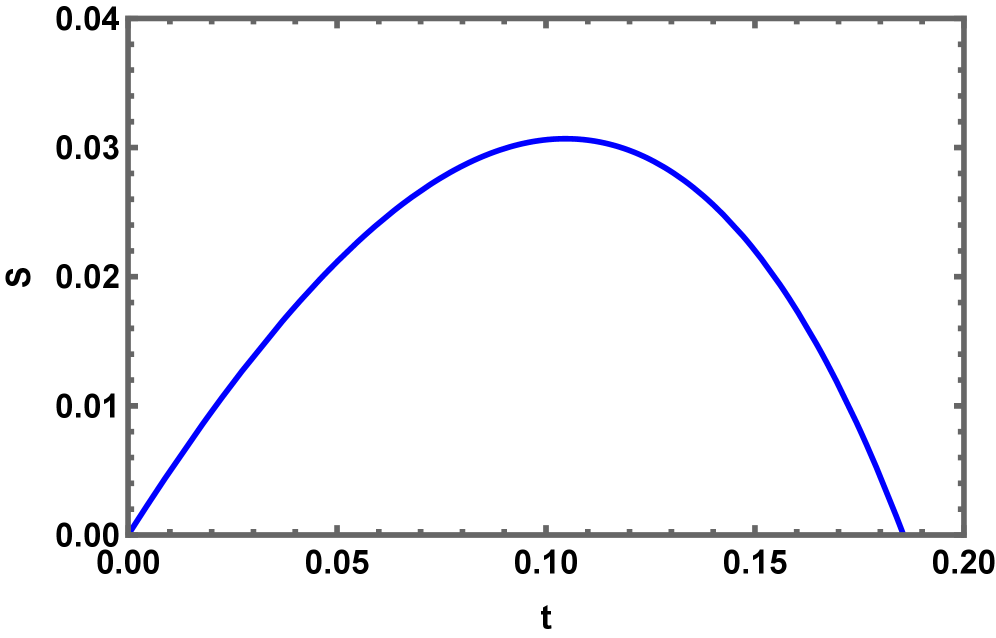
Изолирование чёрной дыры Керра-AdS после взаимодействия с тепловой баней приводит к формированию кривой Пейджа, демонстрирующей различные фазы в зависимости от начального радиуса горизонта - от слабого (a) до промежуточного (b) и малого (c). — Изолирование чёрной дыры Керра-AdS после взаимодействия с тепловой баней приводит к формированию кривой Пейджа, демонстрирующей различные фазы в зависимости от начального радиуса горизонта — от слабого (a) до промежуточного (b) и малого (c).

Статистические ансамбли и будущее восстановления информации

Канонический ансамбль и ансамбль с фиксированной дзета-функцией представляют собой фундаментальные инструменты для исследования термодинамических свойств вращающихся чёрных дыр AdS в процессе фазового перехода. Эти ансамбли позволяют учёным моделировать статистическое поведение микросостояний чёрной дыры, что критически важно для понимания её энтропии, температуры и энергии. В частности, канонический ансамбль предполагает фиксированность числа частиц и позволяет варьировать энергию, в то время как ансамбль с фиксированной дзета-функцией фокусируется на фиксированной величине, связанной с горизонтом событий чёрной дыры. Использование обоих ансамблей в совокупности позволяет получить более полное представление о термодинамике чёрных дыр AdS и их эволюции, что необходимо для дальнейшего исследования парадокса информации и механизмов, посредством которых информация может быть сохранена или восстановлена из чёрной дыры. Результаты, полученные с использованием этих ансамблей, способствуют углублению понимания связи между гравитацией, термодинамикой и квантовой механикой.

Взаимодействие явления суперрадиации с геометрией горизонта событий чёрной дыры оказывает существенное влияние на поведение статистических ансамблей, используемых для изучения термодинамических свойств вращающихся чёрных дыр AdS. Суперрадиация, процесс усиления волн при отражении от вращающегося объекта, приводит к извлечению энергии из чёрной дыры, изменяя её массу и угловой момент. Эта потеря энергии, зависящая от геометрии горизонта, напрямую влияет на статистические свойства ансамблей, таких как канонический и фиксированный дзета-ансамбль. Изменения в геометрии горизонта, вызванные суперрадиацией, модулируют плотность состояний и, следовательно, термодинамическое поведение чёрной дыры, что позволяет более точно описывать фазовые переходы и процессы, связанные с информацией, содержащейся в её горизонте событий. Исследование этой взаимосвязи критически важно для понимания того, как информация кодируется и извлекается из чёрных дыр, что потенциально может пролить свет на разрешение давнего информационного парадокса.

Исследование взаимосвязи между статистическими ансамблями и динамикой черных дыр Керра-AdS открывает новые перспективы для понимания кодирования и восстановления информации, потенциально разрешая давний парадокс информационного исчезновения. Время Пейджа, характеризующее момент начала излучения информации, оказывается зависимым от энтропии черной дыры $S_{BH}$ , скорости света $c$ и температуры Хокинга $T(r+)$ . В свою очередь, время «перемешивания» информации, или время «скрэмблинга», тесно связано с энтропией черной дыры $S_{BH}$ и универсальной константой κ. Углубленное изучение этих количественных связей позволит не только точнее определить механизмы восстановления информации, но и пролить свет на фундаментальные аспекты квантовой гравитации и природу пространства-времени.

Кривая Пейджа для чёрной дыры Керра-AdS в фиксированном ζ ансамбле демонстрирует типичное поведение как для больших, так и для малых чёрных дыр при переходе от взаимодействия с тепловой баней к процессу испарения.

Исследование, представленное в статье, углубляется в парадокс информации чёрных дыр Керра-АдС, рассматривая энтропию запутанности излучения Хокинга. Авторы демонстрируют, что введение ‘островной’ структуры позволяет разрешить этот парадокс, согласуя теоретические выкладки с принципами квантовой механики. Этот подход напоминает слова Фрэнсиса Бэкона: “Знание — сила”. Действительно, стремление понять фундаментальные законы Вселенной, такие как природа чёрных дыр и квантовая гравитация, требует не только математической строгости, но и смелости в принятии новых концепций. Островная формула, предложенная в статье, представляет собой попытку расширить границы нашего знания и приблизиться к разрешению одной из самых сложных загадок современной физики. Работа показывает, что даже кажущаяся потеря информации может быть объяснена при более глубоком анализе квантовых связей.

Что дальше?

Представленная работа, демонстрируя возможность разрешения парадокса информации в контексте вращающихся чёрных дыр Керра-АдС через механизм «островов», лишь обнажает глубину нерешенных вопросов. Расчеты энтропии запутанности, хотя и убедительны, опираются на определенные предположения о структуре пространства-времени вблизи горизонта событий. Иллюзия контроля над математическим аппаратом не должна заслонять тот факт, что сама природа информации и её сохранение в экстремальных гравитационных условиях остаются предметом спекуляций. Даже при идеальной информации, наблюдатель склонен выбирать то, что подтверждает его убеждения, и физика не исключение.

Перспективы дальнейших исследований лежат не только в уточнении численных методов и расширении класса рассматриваемых чёрных дыр. Гораздо интереснее будет исследовать связь между «островами» и другими, казалось бы, не связанными концепциями — например, с квантовой гравитацией, петлевой квантовой гравитацией или даже с теорией категорий. Ведь большинство решений, принимаемых в теоретической физике, — это попытка избежать сожаления о потраченном времени, а не достижение реального прогресса.

В конечном итоге, понимание парадокса информации, вероятно, потребует пересмотра фундаментальных представлений о пространстве, времени и самой природе реальности. И эта переоценка будет не столько математической, сколько психологической — ведь даже самые элегантные модели лишь отражают ограниченность человеческого восприятия.

Оригинал статьи: https://arxiv.org/pdf/2602.03366.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-05 02:00