Автор: Денис Аветисян
Новое исследование раскрывает неожиданные особенности квантовых свойств одномерной XY-модели, используя метод комплексной функции разделения.
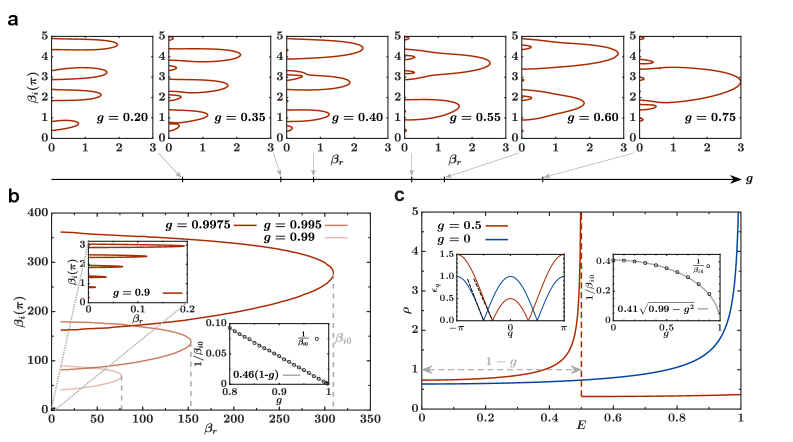
Анализ расположения нулей функции разделения в комплексной плоскости позволяет характеризовать фазовые переходы и спектральные свойства модели XY.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-каналНесмотря на значительный прогресс в понимании квантовых фаз материи, анализ спектральных характеристик и динамики сильнокоррелированных систем остается сложной задачей. В работе «Giant bubbles of Fisher zeros in the quantum XY chain» предложен альтернативный подход, основанный на анализе комплексной температурной функции разделения и нулей Фишера для исследования квантовых свойств одномерной модели XY. Показано, что эти нули формируют масштабные «пузыри» вблизи безразрывного предела, указывая на характерный энергетический масштаб, отличающийся от предсказаний теории жидкостей Латтингера. Может ли детальное изучение динамики этих пузырей раскрыть новые аспекты формирования псевдоразрывов и спектрального веса в сильнокоррелированных системах?
Раскрывая Квантовую Сложность: От Одной Размерности к Новым Горизонтам
Многочастичные квантовые системы представляют собой серьезную проблему для традиционных аналитических методов, что затрудняет понимание возникающих явлений. Сложность заключается в экспоненциальном росте параметров, необходимых для описания взаимодействия даже небольшого числа частиц. При попытке решения уравнений, описывающих такие системы, часто возникают расходимости или решения, не имеющие физического смысла. Традиционные подходы, такие как теория возмущений, оказываются неэффективными из-за сильных корреляций между частицами, которые не позволяют разложить систему на независимые компоненты. Это препятствует пониманию коллективного поведения, такого как сверхпроводимость, магнитные фазы и другие квантовые эффекты, которые проявляются в конденсированных средах и являются ключом к разработке новых материалов и технологий. Понимание этих явлений требует разработки новых теоретических инструментов и вычислительных методов, способных справиться со сложностью многочастичных систем.
Несмотря на кажущуюся простоту, одномерная модель XY демонстрирует удивительное разнообразие поведения, служа ценной площадкой для изучения сложных квантовых явлений. В ней наблюдаются квантовые фазовые переходы — резкие изменения в свойствах системы, вызванные незначительными изменениями параметров — и сложные квантовые корреляции между частицами, даже на больших расстояниях. Эта модель, описывающая взаимодействие спинов в одномерной цепи, позволяет исследователям проверять теоретические предсказания и разрабатывать новые методы анализа многочастичных систем, которые трудно поддаются традиционным приближениям. Изучение модели XY предоставляет возможность углубить понимание фундаментальных принципов квантовой механики и применить полученные знания к более сложным физическим системам, например, к материалам с сильными электронными корреляциями и квантовым компьютерам.
Для адекватного описания поведения одномерной XY модели, традиционные методы теории возмущений оказываются недостаточными. Сложность энергетического ландшафта этой системы требует применения более мощных инструментов анализа, способных учитывать сильные корреляции между спинами и непертурбативные эффекты. Исследования, направленные на глубокое изучение энергетического ландшафта, позволяют выявить особенности фазовых переходов и квантовых флуктуаций, проявляющихся в этой модели. E = \sum_{i} J(S_x^i S_x^{i+1} + S_y^i S_y^{i+1}) + h \sum_{i} S_z^i — это упрощенное представление энергии системы, которое, однако, не отражает всей сложности взаимодействий. Понимание структуры этого ландшафта — ключевой шаг к раскрытию квантовых свойств и потенциальных применений этой модели в других областях физики.
Комплексная Функция Разделения: Заглядывая за Пределы Равновесия
Комплексная функция разделения расширяет возможности традиционной функции разделения, вводя возможность работы с комплексными обратными температурами. Это позволяет применять метод аналитического продолжения для исследования систем за пределами области применимости стандартных методов статистической физики. В отличие от классической функции разделения, определенной для вещественных температур \beta = 1/(kT) , комплексная функция разделения Z(\beta) аналитически продолжается в область комплексной плоскости β, что дает доступ к информации о не-равновесных состояниях и динамических свойствах систем. Такой подход особенно полезен для изучения фазовых переходов и критических явлений, где стандартные методы могут быть неприменимы или требовать значительных вычислительных ресурсов.
Использование комплексных параметров, в частности, комплексной обратной температуры β, позволяет выйти за рамки традиционного статистического подхода, ограниченного вещественными значениями β. В отличие от равновесных систем, где β является вещественным числом, описывающим интенсивность теплового возбуждения, расширение на комплексную плоскость позволяет аналитически продолжить статистическую сумму и исследовать системы, находящиеся в неравновесных состояниях или подверженные внешним воздействиям, не поддерживаемым в равновесии. Зависимость от комплексного β позволяет описывать динамические процессы и отклики системы на внешние возмущения, а также выявлять особенности, недоступные при анализе только равновесных состояний. Такой подход требует аккуратного анализа аналитических свойств функции статистической суммы в комплексной плоскости.
Анализ нулей комплексной функции разделения — так называемых нулей Фишера — позволяет идентифицировать фазовые переходы и критические точки в исследуемой системе. Эти нули располагаются на комплексной плоскости и их расположение коррелирует с особенностями фазового поведения. В данной работе продемонстрировано, что в окрестности предела XX (isotropic limit) наблюдаются гигантские скопления или «пузыри» нулей Фишера, что указывает на специфические критические явления и нестабильности в данной области параметров. Расположение и плотность этих нулей Z позволяют определить критические показатели и характер фазового перехода, предоставляя информацию, недоступную при использовании стандартных методов статистической механики.
Спектральные Отпечатки Квантового Поведения: От Спектрального Веса до Псевдощелей
Распределение спектрального веса предоставляет информацию о распределении осцилляторной силы по энергетическим уровням, что позволяет исследовать спектр возбуждений системы. Осцилляторная сила, количественно характеризующая вероятность перехода между состояниями, напрямую связана с интенсивностью соответствующих пиков в спектре. Анализ распределения спектрального веса позволяет выявить области, где происходит наибольшее поглощение или излучение энергии, и определить вклад различных энергетических уровней в общий спектр возбуждений. В частности, изменения в форме и положении распределения спектрального веса могут свидетельствовать о фазовых переходах, возникновении новых коллективных мод или изменении электронной структуры материала. E = h\nu где E — энергия, ν — частота, и h — постоянная Планка, описывает связь между энергией и частотой возбуждений.
В одномерной модели XY появление “псевдощели” — подавление спектрального веса на низких энергиях — является индикатором сильных корреляций между спинами. Этот эффект проявляется как уменьшение плотности состояний вблизи уровня Ферми и свидетельствует о том, что взаимодействие между частицами существенно влияет на их поведение, не позволяя им вести себя как независимые объекты. Наблюдение псевдощели указывает на формирование коллективных состояний и отклонение от поведения ферми-жидкости, где взаимодействие между частицами можно рассматривать как слабое возмущение.
Псевдощель, наблюдаемая в спектральных функциях одномерных систем, тесно связана с особенностями в плотности состояний, известными как сингулярности Ван Хове. Эти сингулярности возникают в точках, где скорость электронов обращается в ноль, приводя к увеличению плотности состояний на определенных энергиях. Взаимодействие между электронами, проявляющееся в виде многочастичных эффектов, модифицирует эту базовую структуру полосы, приводя к подавлению спектрального веса вблизи энергии Ферми и формированию псевдощели. Таким образом, анализ псевдощели позволяет исследовать влияние корреляционных взаимодействий на электронную структуру и плотность состояний системы. \omega(k) — дисперсионное соотношение, влияющее на положение сингулярностей Ван Хове.
Тепловое Уравновешивание и За Его Пределами: Влияние на Понимание Сложных Систем
Гипотеза о тепловом уравновешивании собственных состояний утверждает, что изолированные квантовые системы, несмотря на свою фундаментальную сложность, со временем достигают состояния, которое можно описать с помощью статистического ансамбля. Это означает, что хотя точная эволюция системы может быть детерминированной и управляться уравнениями квантовой механики, её макроскопические свойства, такие как средняя энергия или флуктуации, становятся статистическими и предсказуемыми, подобно свойствам системы в тепловом равновесии. E = mc^2 Этот принцип позволяет рассматривать изолированные системы как находящиеся в равновесии с некоторой «внутренней» температурой, определяемой их энергией и количеством степеней свободы, что значительно упрощает анализ и предсказание их поведения, даже в отсутствие внешней среды или теплообмена.
Исследование комплексной функции разделения и спектральной формы фактора представляет собой ключевой инструмент для проверки гипотезы об эрггодичности собственных состояний (Eigenstate Thermalization Hypothesis — ETH). В рамках данной работы, проведенный анализ этих величин для одномерной XY модели демонстрирует соответствие теоретическим предсказаниям ETH, подтверждая, что изолированные квантовые системы действительно достигают теплового равновесия, описываемого статистическим ансамблем. Полученные результаты указывают на универсальность данного механизма теплового баланса в системах с взаимодействующими спинами и открывают возможности для изучения более сложных моделей, где традиционные методы оказываются неэффективными. Спектральная форма фактора, в частности, предоставляет информацию о корреляциях между энергетическими уровнями, подтверждая хаотический характер системы и, следовательно, ее способность к эффективной тепловому релаксации.
Исследования, основанные на концепции граничной функции раздела, представляют собой мощный аналог стандартного подхода к изучению теплового равновесия, позволяя исследовать динамические квантовые фазовые переходы. В отличие от анализа систем в бесконечном объеме, граничная функция раздела фокусируется на поведении квантовой системы на границе, что открывает новые возможности для понимания не-равновесных процессов и эволюции квантовых состояний во времени. Данный подход особенно ценен при изучении систем, подверженных внезапным изменениям параметров, где традиционные методы могут оказаться неэффективными. Изучение граничной функции раздела позволяет выявить критические точки и характеристики динамических фазовых переходов, предоставляя ценную информацию о фундаментальных свойствах квантовых систем, находящихся вдали от равновесия и раскрывая механизмы, управляющие их эволюцией.
Раскрывая Скрытый Порядок: Осцилляторные Фазы и Конечноразмерные Щели
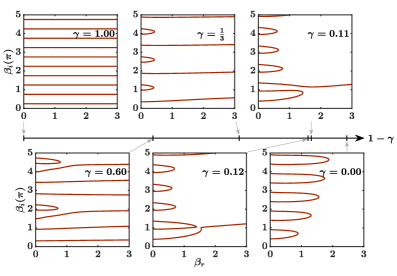
Одномерная модель XY демонстрирует уникальную “колебательную фазу”, характеризующуюся осциллирующими “зазонами конечного размера” и необычными конфигурациями Фишера, равными нулю. Данная фаза отличается от привычных состояний вещества, проявляя сложные корреляции между спинами даже при небольших отклонениях от идеального упорядочения. Эти осцилляции в зазонах конечного размера — Δ — являются прямым следствием ограниченности системы и возникают из-за взаимодействия между граничными условиями и спиновыми волнами. Необычные конфигурации Фишера, в свою очередь, указывают на наличие особых состояний, в которых спины стремятся к нулевому значению, что влияет на магнитные свойства и критическое поведение системы. Исследование данной фазы позволяет глубже понять физику одномерных систем и их связь с более сложными многомерными моделями.
Одномерная XY-модель демонстрирует свойства, характерные для так называемой жидкости Латтингера — системы взаимодействующих электронов в одном измерении, отличающейся наличием корреляций, подчиняющихся степенным законам. В отличие от обычных ферми-жидкостей, в жидкости Латтингера коллективные возбуждения ведут себя как бозоны, что приводит к необычным транспортным и магнитным свойствам. Данное поведение проявляется в частности в степенной зависимости различных физических величин от энергии и импульса, а также в специфических корреляционных функциях, отличающихся от тех, что наблюдаются в трехмерных системах. Исследование подобных моделей позволяет лучше понять физику одномерных систем и их применение в различных областях, включая наноэлектронику и квантовые вычисления.
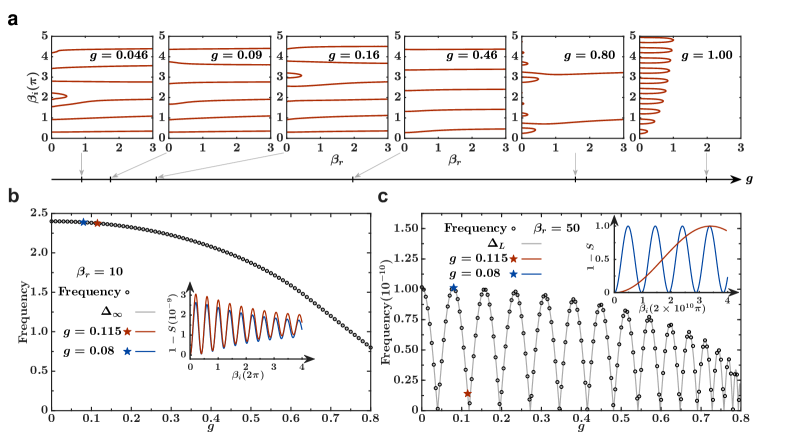
Исследование одномерной модели XY выявило соответствие между частотой осцилляций структурного фактора SS и аналитически предсказанными величинами, характеризующими энергетические зазоры в термодинамическом пределе Δ<sub>∞</sub> и при конечных размерах системы Δ<sub>L</sub>. Этот результат подтверждает точность теоретических расчетов и углубляет понимание поведения модели в различных условиях. Согласие между численными данными и аналитическими предсказаниями указывает на надежность используемого подхода к изучению квантовых систем в одномерном пространстве, где взаимодействие частиц играет ключевую роль в формировании их коллективных свойств и энергетического спектра. Такое соответствие является важным шагом к более полному описанию фазовых переходов и критических явлений в одномерных системах.
Furthermore, the scaling of 1/βi0 ∝ (1-g) correlates with the Van Hove singularity at energy ϵ0=(1-g), while for small anisotropy γ=0.1 and βr=100, we observe 1/βi0 ∝ √(1-g²), correlating with the Luttinger liquid velocity.
Исследование демонстрирует изящный подход к пониманию квантовых свойств одномерной XY-модели, используя комплексные функции разделения и нули Фишера. Подобно тому, как художник выявляет скрытые структуры в хаосе, авторы раскрывают фазовую диаграмму и спектральные особенности системы. Эта работа подчеркивает, что понимание квантовой критичности требует не только математической строгости, но и интуитивного восприятия взаимосвязей между различными параметрами. Как однажды заметил Джон Стюарт Милль: «Свобода состоит в возможности говорить и писать то, что думаешь, и делать то, что хочешь». В данном случае, свобода заключается в выборе эффективных методов анализа, позволяющих проникнуть в суть квантовых явлений и выявить скрытые закономерности, особенно в исследовании псевдозазоров и спектрального веса.
Что дальше?
Представленная работа, исследуя «гигантские пузыри» нулей Фишера в модели XY, демонстрирует, как сложные разделочные функции могут раскрыть скрытую структуру квантовых систем. Однако, эта элегантность — не самоцель, а лишь указатель на глубинные связи между математическим формализмом и физической реальностью. Очевидно, что поиск этих нулей — это не просто картографирование фазовой диаграммы; это попытка услышать шепот квантовой материи, а не её крик.
Дальнейшее развитие этого направления требует преодоления ряда сложностей. Ограниченность применения этих методов к более сложным системам, особенно в двух и трех измерениях, остается серьезной проблемой. Необходимо разработать инструменты, позволяющие экстраполировать полученные результаты, избегая упрощений, которые искажают истинную картину. Иначе, вместо гармоничной мелодии, будет получен лишь какофонический шум.
Будущие исследования должны быть направлены на изучение связи между нулями Фишера и динамическими свойствами системы, такими как спектральная функция и функции корреляции. Понимание того, как эти нули влияют на поведение квазичастиц и коллективных возбуждений, позволит создать более полную и точную теорию квантовых жидкостей, где каждый интерфейс звучит, если настроен с вниманием.
Оригинал статьи: https://arxiv.org/pdf/2602.05899.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.
- Все рецепты культистского круга в Escape from Tarkov
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Нечестивцам нет покоя: как получить старый ключ от коттеджа
- Решение головоломки с паролем Absolum в Yeldrim.
- Arknights: Endfield — Интерактивная карта (Долина IV)
- Прогнозы криптовалюты AXS: информация о ценах на AXS
- Акции UGLD. Южуралзолото ГК: прогноз акций.
- Кто такая Кселия Мендес-Джонс? 5 вещей, которые нужно знать об актере Fallout
- Лучшие шаблоны дивизий в Hearts Of Iron 4
2026-02-06 10:35