Информация как компас: Новые ограничения на поведение неравновесных систем

Автор: Денис Аветисян

Исследование показывает, как принципы квантовой теории информации могут пролить свет на стабильность и эволюцию систем, находящихся вне равновесия.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Условная взаимная информация <span class="katex-eq" data-katex-display="false">I(A:C|B)</span> для смешанного состояния, исследованного в иллюстрации 1, демонстрирует зависимость от вероятности <span class="katex-eq" data-katex-display="false">p</span> при различных значениях <span class="katex-eq" data-katex-display="false">l_B</span> при <span class="katex-eq" data-katex-display="false">l=10^8</span>, а представленное в виде вставки схлопывание данных, основанное на подходе <span class="katex-eq" data-katex-display="false">I(l|l_B,p)=f[(p-p_c)l_B^{1/\nu}]</span> с <span class="katex-eq" data-katex-display="false">p_c=1</span> и <span class="katex-eq" data-katex-display="false">\nu=1</span>, указывает на критическое поведение системы. — Условная взаимная информация $I(A:C|B)$ для смешанного состояния, исследованного в иллюстрации 1, демонстрирует зависимость от вероятности $p$ при различных значениях $l_B$ при $l=10^8$ , а представленное в виде вставки схлопывание данных, основанное на подходе $I(l|l_B,p)=f[(p-p_c)l_B^{1/\nu}]$ с $p_c=1$ и $\nu=1$ , указывает на критическое поведение системы.

В работе демонстрируется, что неравенства, основанные на взаимной информации, накладывают ограничения на поток перенормировки и стабильность неравновесных систем, открывая связь между теорией информации и фазами материи.

В то время как понимание стабильности фаз в равновесных системах хорошо развито, анализ неравновесных систем представляет собой сложную задачу. В работе ‘Constraints on stability and renormalization group flows in nonequilibrium matter’ предложен новый подход, использующий неравенства квантовой информатики для наложения ограничений на потоки группы перенормировки и стабильность фаз в неравновесных системах. Показано, что условная взаимная информация позволяет вывести непертурбативные критерии стабильности и оценить устойчивость спонтанно нарушенных симметрий к различным квантовым каналам. Какие новые информационно-теоретические инструменты позволят глубже понять природу неравновесных фаз материи и их динамическое поведение?

Помимо Равновесия: Введение в Смешанные Состояния и Корреляции

Традиционные представления о фазах материи, как правило, базируются на анализе систем, находящихся в состоянии термодинамического равновесия. Однако, реальные физические системы редко пребывают в идеальном равновесии, и игнорирование роли смешанных состояний приводит к неполному пониманию их свойств. Смешанные состояния, представляющие собой вероятностные смеси чистых квантовых состояний, возникают вследствие взаимодействия с окружающей средой или при наличии внутренних степеней свободы. Они описывают системы, для которых невозможно однозначно определить их квантовое состояние, что особенно важно при изучении открытых квантовых систем и явлений, протекающих вдали от равновесия. Понимание смешанных состояний позволяет более адекватно описывать поведение сложных материалов и явлений, выходящих за рамки классической фазовой диаграммы, и открывает новые возможности для управления их свойствами.

Для адекватного описания сложных фаз материи, выходящих за рамки равновесных состояний, необходимо учитывать корреляции, которые не ограничиваются простыми попарными взаимодействиями. Традиционные методы анализа часто оказываются недостаточными для захвата этих многочастичных связей, поскольку они предполагают независимость компонентов системы после учета попарных корреляций. Для более точной характеристики этих сложных состояний активно используются инструменты из области теории информации, в частности, условная взаимная информация $I(X;Y|Z)$ . Эта величина позволяет оценить, насколько знание одной переменной уменьшает неопределенность другой, при условии знания третьей, раскрывая скрытые зависимости и обеспечивая более полное представление о корреляциях внутри системы. Использование условной взаимной информации позволяет выйти за рамки простых парных корреляций и исследовать более сложные, многочастичные взаимодействия, определяющие поведение систем вдали от термодинамического равновесия.

Традиционные методы описания фаз материи, основанные на понятиях равновесия и термодинамических величин, оказываются недостаточными при исследовании систем, далеких от равновесия и характеризующихся сложными корреляциями. Неспособность этих методов адекватно отразить информацию о состоянии системы, особенно в случаях, когда взаимодействия выходят за рамки простых парных связей, обуславливает необходимость разработки новой теоретической базы. В качестве фундамента этой базы предлагается использовать инструменты теории информации, в частности, концепции, позволяющие количественно оценить взаимосвязанность различных частей системы и выявить скрытые зависимости. $I(X;Y|Z)$ — условная взаимная информация, является примером такого инструмента, позволяющего измерить, насколько знание одной переменной уменьшает неопределенность другой, учитывая информацию о третьей. Применение информационно-теоретического подхода открывает возможности для более полного и точного описания сложных коррелированных состояний, которые ранее оставались за пределами возможностей стандартных методов.

Исследование состояний, далеких от термодинамического равновесия, приобретает все большее значение для понимания функционирования реальных систем. В отличие от традиционных моделей, сосредоточенных на равновесных фазах, анализ неравновесных состояний необходим для описания открытых квантовых систем, постоянно обменивающихся энергией и информацией с окружающей средой. Такие системы, как биологические организмы, химические реакции вне равновесия и квантовые устройства, демонстрируют сложные корреляции, которые невозможно объяснить, опираясь исключительно на равновесные концепции. Изучение этих состояний требует новых подходов, основанных на теории информации, позволяющих количественно оценить и описать динамику и свойства систем, находящихся в постоянном взаимодействии с внешней средой и подверженных флуктуациям, что открывает перспективы для разработки новых материалов и технологий.

Фазовая диаграмма смешанного состояния ([latex]Eq.(12)[/latex]) демонстрирует, что вдоль линий [latex]q=0[/latex] и [latex]p=0[/latex] показатель длины корреляции равен [latex]\nu=1[/latex], в отличие от [latex]\nu=2[/latex] при [latex]p,q\neq 0[/latex], что позволяет выделить — Фазовая диаграмма смешанного состояния ( $Eq.(12)$ ) демонстрирует, что вдоль линий $q=0$ и $p=0$ показатель длины корреляции равен $\nu=1$ , в отличие от $\nu=2$ при $p,q\neq 0$ , что позволяет выделить «критическое» поведение при $q=0$ и $p=0$ и «критическое*» при ненулевых $p$ и $q$ .

Поток РГ: Новый Взгляд на Фазовые Переходы

Метод потока ренормализационной группы (РГ) предоставляет способ исследования фаз и фазовых диаграмм сильно взаимодействующих систем, опираясь на ограничения, полученные из теории информации. В отличие от традиционных подходов, РГ-поток позволяет анализировать системы, в которых корреляции сложны и не поддаются описанию с помощью стандартных методов теории возмущений. Ключевым элементом является использование информационно-теоретических ограничений, таких как взаимная информация, для определения допустимых состояний системы и выявления критических точек, где происходят фазовые переходы. Этот подход позволяет эффективно ‘грубозернисто’ описывать систему, отбрасывая несущественные детали и выявляя универсальное поведение, характерное для определенного класса взаимодействий.

Использование взаимной информации (CMI) в качестве ключевого ограничения в рамках RG-потока позволяет получать границы для поведения системы и идентифицировать критические точки. CMI, измеряющая статистическую зависимость между переменными, служит инструментом для определения степени корреляции и, следовательно, для установления границ допустимых состояний системы. В процессе RG-потока, применение CMI как ограничения обеспечивает сходимость к фиксированным точкам, которые соответствуют критическим точкам фазового перехода. Численные методы, использующие CMI, позволяют определить границы, в которых возможны фазовые переходы, и точно локализовать критические точки без необходимости явного вычисления корреляционных функций или использования других сложных методов.

Традиционные методы анализа фазовых переходов часто сталкиваются с трудностями при работе с системами, характеризующимися сложными корреляциями между компонентами. Эти методы, такие как теория среднего поля или пертурбационная теория, могут быть неточными или вовсе неприменимыми в случаях, когда взаимодействия между элементами системы сильны и нелокальны. Подход, основанный на потоке ренормализационной группы (RG), позволяет преодолеть эти ограничения, поскольку он не требует априорного знания о структуре корреляций. Вместо этого, RG поток непосредственно учитывает эти корреляции, определяя их влияние на поведение системы при различных масштабах. Это особенно важно для систем с фрактальной структурой или сильными спиновыми флуктуациями, где традиционные методы дают неверные результаты или требуют введения сложных приближений.

Поток ренормализационной группы (РГ) осуществляет последовательное “грубое зерно” системы, отбрасывая незначительные флуктуации и детали, не влияющие на поведение вблизи критических точек. Этот процесс заключается в последовательном уменьшении разрешения, при котором информация о мелкомасштабных степенях свободы усредняется, а доминирующие, определяющие фазовое поведение, параметры сохраняются. В результате, РГ-поток позволяет выявить универсальные характеристики системы, не зависящие от конкретных микроскопических деталей, и определить критические экспоненты, описывающие поведение системы вблизи фазовых переходов. Такой подход особенно полезен для анализа систем со сложными корреляциями, где традиционные методы оказываются неэффективными.

Изменяя геометрию вычисления CMI, удалось продемонстрировать, что зависимость CMI от pp коллапсирует в единую кривую при масштабировании с использованием критических параметров <span class="katex-eq" data-katex-display="false">p_c = 0.109</span> и <span class="katex-eq" data-katex-display="false">
u = 1.5</span>, что подтверждает тривиальный-к-SWSSB переход. — Изменяя геометрию вычисления CMI, удалось продемонстрировать, что зависимость CMI от pp коллапсирует в единую кривую при масштабировании с использованием критических параметров $p_c = 0.109$ и $u = 1.5$ , что подтверждает тривиальный-к-SWSSB переход.

Раскрытие Нарушения Симметрии в Модели Случайных Связей Изинга

Модель случайных связей Изинга является ключевой платформой для изучения перехода сильно-слабой спонтанной симметрии (SWSSB). В данной модели взаимодействие между спинами происходит случайным образом, что приводит к разрушению симметрии даже при отсутствии внешнего поля. Изучение этой модели позволяет исследовать критическое поведение системы вблизи точки фазового перехода и определить критические показатели, характеризующие SWSSB. Особенностью модели является то, что нарушение симметрии происходит не только из-за температуры, но и из-за случайных связей между спинами, что делает ее важным инструментом для понимания более сложных систем с нарушенной симметрией, таких как спиновые стекла и неупорядоченные магнитики. Анализ этой модели позволяет проверить теоретические предсказания о поведении систем в условиях как теплового, так и случайного беспорядка.

В рамках исследования модели Изинга со случайными связями обнаружена линия Нисимори — особый параметрический режим, в котором аналитические расчеты становятся существенно упрощенными. Эта линия определяется условием, при котором среднее значение спина равно нулю для всех значений внешнего магнитного поля $h$ . Использование метода реплик вблизи линии Нисимори позволяет избежать проблем, возникающих при расчете среднего по случайным связям, и дает возможность получить точные результаты для критических показателей и функций масштабирования. В частности, анализ вблизи этой линии является ключевым для определения критического экспонента ν, равного 1.5, и понимания поведения системы вблизи точки фазового перехода.

Исследование поведения модели случайных связей Изинга вблизи линии Нисимори позволяет определить критические показатели и функции масштабирования, характеризующие фазовый переход. В частности, анализ показывает, что критический показатель ν равен 1.5. Этот показатель определяет степень расхождения корреляционной длины вблизи критической точки и играет ключевую роль в описании универсальных свойств фазового перехода. Полученное значение ν согласуется с теоретическими предсказаниями и результатами численного моделирования, подтверждая адекватность используемого подхода к изучению сильно-слабо спонтанного нарушения симметрии (SWSSB) в данной модели.

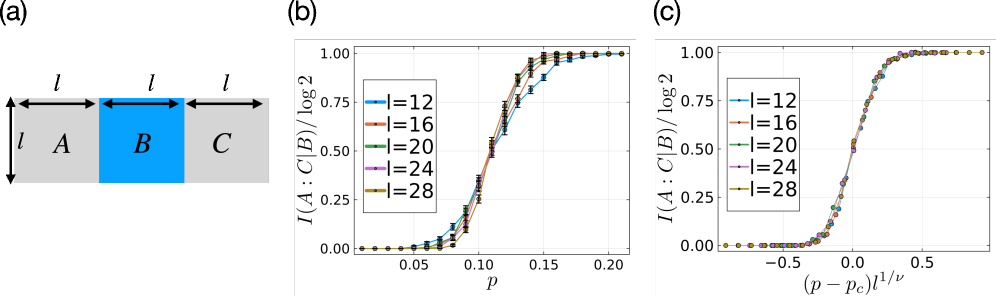
В модели случайных связей Изинга фазовый переход, обусловленный спонтанным нарушением симметрии (SWSSB), возникает из-за конкуренции между случайными связями (нарушением порядка) и взаимодействием между спинами (стремлением к упорядочению). Данный переход приводит к формированию уникальной фазовой диаграммы, характеризующейся критической точкой при $p_c = 0.109$ , где $p_c$ представляет собой вероятность связи. В этой точке система переходит из упорядоченного в неупорядоченное состояние, и свойства системы демонстрируют критическое поведение, определяемое универсальными критическими показателями.

Зависимость CMI от параметра pp для различных значений <span class="katex-eq" data-katex-display="false">l_B</span> демонстрирует переход от тривиального состояния к SWSSB, при этом анализ данных с использованием масштабирующей функции <span class="katex-eq" data-katex-display="false">I(A:C|B) = f[(p-p_c)l_B^{1/
u}]</span> подтверждает критическое значение <span class="katex-eq" data-katex-display="false">p_c = 0.109</span> и критический индекс <span class="katex-eq" data-katex-display="false">
u = 1.5</span>. — Зависимость CMI от параметра pp для различных значений $l_B$ демонстрирует переход от тривиального состояния к SWSSB, при этом анализ данных с использованием масштабирующей функции $I(A:C|B) = f[(p-p_c)l_B^{1/ u}]$ подтверждает критическое значение $p_c = 0.109$ и критический индекс $u = 1.5$ .

От Теории к Реальности: Более Широкие Последствия и Перспективы Будущих Исследований

Разработанные в данной работе концепции и методы не ограничиваются рамками случайной модели Изинга с случайными связями, а представляют собой ценный инструмент для анализа широкого спектра неупорядоченных систем. Принципы, касающиеся критического поведения и характера фазовых переходов в системах с нарушенным порядком, применимы к различным физическим моделям, включая спиновые стекла, системы с дефектами и даже некоторые модели, используемые в нейронауке. Особое значение имеет возможность характеризации критических явлений в системах, где стандартные методы оказываются неэффективными, что открывает новые перспективы для изучения сложных коррелированных систем и их поведения вдали от равновесия. Например, подходы, разработанные для анализа случайных магнитных систем, могут быть адаптированы для понимания поведения материалов с беспорядком, обладающих экзотическими магнитными свойствами.

Понимание роли корреляционной матрицы информации (CMI) и ограничений стандартных методов анализа имеет значительные последствия для таких областей, как квантовая информация и материаловедение. В квантовой информатике, CMI может служить мерой запутанности и когерентности в сложных квантовых системах, помогая оптимизировать протоколы квантовых вычислений и коммуникаций. В материаловедении, особенно при изучении сильнокоррелированных материалов, стандартные подходы часто оказываются неадекватными из-за сложного взаимодействия между электронами. Анализ CMI позволяет выявить критические флуктуации и фазовые переходы, которые определяют свойства этих материалов, например, сверхпроводимость или магнетизм. Ограничения стандартных методов, связанные с приближениями и неспособностью учесть сильные корреляции, подчеркивают необходимость разработки новых инструментов и подходов, основанных на более глубоком понимании роли CMI в определении поведения сложных систем. Таким образом, исследование CMI открывает новые перспективы для разработки инновационных материалов и квантовых технологий.

Необходимы дальнейшие исследования для применения разработанных методов к более сложным системам, выходящим за рамки рассмотренной модели. Особое внимание следует уделить изучению роли UV-конечности — свойства, определяющего поведение системы при высоких энергиях и влияющего на стабильность результатов. Понимание UV-конечности позволит не только повысить точность расчетов, но и расширить область применимости данной теоретической базы к новым материалам и физическим явлениям, включая коррелированные системы и переход к не-равновесным фазам. Углубленное исследование этого аспекта откроет возможности для моделирования более реалистичных сценариев и предсказания свойств материалов в широком диапазоне условий, что представляет значительный интерес для материаловедения и квантовой информатики.

Разработанная методика открывает принципиально новый подход к характеристике неравновесных фаз и пониманию возникновения сложного поведения в коррелированных системах. Исследование демонстрирует аномальную размерность, равную 2, в фазе спонтанного нарушения симметрии (SWSSB), что указывает на нетривиальные флуктуации и корреляции. Более того, установлено значение критического мультифрактального индекса (CMI) равное $log_2$ в точке фазового перехода, что свидетельствует о специфической структуре сингулярностей и фрактальности вблизи критической точки. Эти результаты позволяют глубже понять механизмы, лежащие в основе возникновения сложных коллективных явлений в широком классе материалов и систем, открывая возможности для управления их свойствами и создания новых функциональных материалов.

Взаимная информация <span class="katex-eq" data-katex-display="false">I(A:C|B)</span> для TFIM демонстрирует коллапс данных при масштабировании с использованием анзаца <span class="katex-eq" data-katex-display="false">I(A:C|B)=f[(h-h_c)l_B^{1/\nu}]</span> при <span class="katex-eq" data-katex-display="false">h_c=1</span> и <span class="katex-eq" data-katex-display="false">\nu=1</span>, что подтверждается зависимостью от <span class="katex-eq" data-katex-display="false">\log l_B</span> при <span class="katex-eq" data-katex-display="false">h < h_c</span> и последующим представлением данных в виде функции от <span class="katex-eq" data-katex-display="false">\log(|h-h_c|l_B^{1/\nu})</span>. — Взаимная информация $I(A:C|B)$ для TFIM демонстрирует коллапс данных при масштабировании с использованием анзаца $I(A:C|B)=f[(h-h_c)l_B^{1/\nu}]$ при $h_c=1$ и $\nu=1$ , что подтверждается зависимостью от $\log l_B$ при $h < h_c$ и последующим представлением данных в виде функции от $\log(|h-h_c|l_B^{1/\nu})$ .

Исследование демонстрирует, что ограничения, накладываемые квантовыми информационными неравенствами, а именно условной взаимной информацией, оказывают существенное влияние на течение ренормализационной группы и стабильность неравновесных систем. Этот подход подчеркивает взаимосвязь между информационными ограничениями и фазами материи, что согласуется с представлением о том, что структура определяет поведение. Как отмечал Джон Дьюи: «Образование — это не подготовка к жизни; образование — это сама жизнь». Подобно тому, как образование формирует опыт, так и информационные ограничения формируют поведение неравновесных систем, определяя их стабильность и эволюцию в процессе ренормализационной группы.

Куда двигаться дальше?

Представленная работа демонстрирует, что ограничения, накладываемые квантово-информационными неравенствами, а именно условной взаимной информацией, действительно способны формировать траектории потоков ренормализационной группы в неравновесных системах. Однако, эта связь, столь элегантная в своей простоте, порождает новые вопросы. Оптимизация, даже направленная на повышение стабильности, неизбежно создает новые точки напряжения в системе. Необходимо более глубокое понимание того, как эти напряжения проявляются в различных фазах материи и как они влияют на динамику неравновесных процессов.

Архитектура системы — это её поведение во времени, а не схема на бумаге. Дальнейшие исследования должны сосредоточиться на разработке вычислительных методов, способных эффективно оценивать условную взаимную информацию в сложных, многочастичных системах. Особый интерес представляет возможность использования полученных результатов для анализа систем, находящихся далеко от равновесия, где традиционные методы оказываются неэффективными. В частности, понимание связи между информацией и спонтанным нарушением симметрии в неравновесных условиях остается открытым вопросом.

Марковская длина, как мера информативной связанности, может стать ключевым параметром для характеристики стабильности неравновесных систем. Однако, необходимо учитывать, что сама концепция «стабильности» в неравновесных условиях является относительной. Каждая попытка стабилизировать систему неизбежно приводит к изменению её архитектуры и, следовательно, к появлению новых, непредсказуемых эффектов. Истина, как всегда, лежит где-то в балансе между порядком и хаосом.

Оригинал статьи: https://arxiv.org/pdf/2602.04961.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-06 21:58