Хаос в Квантовом Мире: Магнитные Поля Как Ключ к Управлению

Автор: Денис Аветисян

---

Новое исследование показывает, как внешние магнитные поля влияют на хаотическое поведение квантовых систем, открывая возможности для тонкой настройки динамики рассеяния.

Работа посвящена исследованию влияния поперечных магнитных полей на квантический хаос в бильярдах, демонстрируя связь между движением в направляющих координатах и подавлением хаотичности.

Несмотря на значительный прогресс в понимании квантического хаоса, влияние внешних магнитных полей на динамику скремблирования информации в квантовых системах остается недостаточно изученным. В работе ‘More on OTOCs and Chaos in Quantum Mechanics — Magnetic Fields’ исследуется поведение тепловых вневременных корреляторов (OTOC) в одночастичных квантовых системах, моделируемых магнитными бильярдами. Показано, что поперечное магнитное поле позволяет контролировать динамику скремблирования и выявляет переход от квантического хаоса к магнитной жесткости, при этом динамика, описываемая с помощью координат ведущего центра, демонстрирует качественно иное поведение. Какие новые возможности для управления квантической информацией открывает сочетание геометрии и магнитных полей?

---

Шёпот Хаоса: Поиск Инструментов для Квантовой Неопределённости

Понимание перехода от квантового поведения к классическому требует разработки инструментов для характеристики квантического хаоса. Это связано с тем, что в сложных квантовых системах информация перетасовкивается и рассеивается, что делает невозможным предсказание будущего состояния системы на основе её начальных условий, подобно тому, как это происходит в классическом хаотичном мире. Для описания этой «перетасовки» необходимы методы, способные измерять не просто корреляции между различными параметрами системы в один момент времени, а так называемые вневременные корреляции — то есть, насколько сильно связаны параметры системы в разные моменты времени. Именно эти вневременные корреляции позволяют количественно оценить степень хаотичности квантовой системы и проследить, как она эволюционирует от чисто квантового поведения к классическому, что открывает возможности для изучения фундаментальных аспектов физики и разработки новых технологий, основанных на квантовых принципах.

Традиционные методы анализа квантовых систем зачастую оказываются неэффективными при попытке количественно оценить перемешивание информации в сложных условиях. В то время как простые системы демонстрируют предсказуемое поведение, увеличение числа взаимодействующих частиц приводит к экспоненциальному росту сложности, делая стандартные подходы, основанные на вычислении траекторий или спектральных характеристик, практически неприменимыми. Проблема заключается в том, что информация, изначально локализованная в определенной части системы, быстро распространяется и запутывается, теряя свою первоначальную структуру. Это явление, известное как квантовое перемешивание, происходит гораздо быстрее, чем в классических системах, и его точное измерение требует новых, более чувствительных методов, способных уловить тонкие корреляции между различными частями системы, даже когда прямая связь между ними отсутствует.

Для исследования процесса «квантового хаоса» и, в частности, рассеяния информации в сложных квантовых системах, необходимы методы, чувствительные к так называемым «вне-временным корреляциям». Эти корреляции, в отличие от традиционных, измеряют, как сильно изменения в одном месте системы влияют на другие места не во времени, а в противоположном порядке. C(t_1, t_2) = \langle A(t_1)B(t_2) \rangle — типичное выражение для корреляционной функции, где t_1 и t_2 представляют моменты времени. Анализ этих корреляций позволяет установить, насколько быстро информация «перемешивается» внутри системы, что является ключевым индикатором степени хаотичности. Изучение вне-временных корреляций предоставляет уникальный инструмент для понимания перехода от квантового к классическому поведению, позволяя количественно оценить, как быстро теряется предсказуемость в сложных квантовых системах.

Формализм Хашимото: Строим Мост к Вычислениям

Формализм, разработанный Хашимото и соавторами, представляет собой ключевую основу для вычисления OTOC (Out-of-Time-Ordered Correlation functions) в одночастичных системах. Этот подход базируется на использовании функции Грина и позволяет аналитически и численно вычислять OTOC для различных потенциалов. В частности, он предоставляет возможность изучения динамики хаоса и тепловых свойств систем, описываемых гамильтонианом, содержащим одночастичные взаимодействия. Ключевым элементом является вычисление G(t, t') — функции Грина, определяющей эволюцию во времени волновой функции и позволяющей определить степень чувствительности системы к малым возмущениям, что напрямую связано с расчетом OTOC.

Применение формализма Хашимото и соавторов к системам, подверженным внешним воздействиям, таким как магнитные поля, сталкивается со значительными трудностями. Основная проблема заключается в нарушении инвариантности относительно трансляций, что является ключевым допущением в исходной формулировке. Введение внешних сил приводит к появлению дополнительных членов в гамильтониане и, как следствие, к усложнению вычисления корреляторов порядка времени (OTOCs). Необходима модификация подхода, учитывающая влияние внешнего поля на динамику системы и обеспечивающая корректное вычисление OTOCs в присутствии этих сил. Простое добавление членов, связанных с внешним полем, не всегда приводит к корректным результатам, и требуется более глубокий анализ динамики системы.

Для расширения вычислений ОТК (Out-of-Time-ordered Correlation functions) в системах, подверженных внешним воздействиям, необходимо учитывать динамику формирования уровней Ландау. Уровни Ландау — это квантованные энергетические уровни электронов в магнитном поле, возникающие вследствие дискретизации траекторий движения электронов, обусловленной лоренцевой силой. Их появление приводит к модификации спектральных свойств системы и, следовательно, влияет на величину ОТК. Корректный учет этих уровней требует анализа движения электронов в постоянном магнитном поле B и вычисления соответствующих волновых функций, что, в свою очередь, усложняет математический аппарат, используемый для вычисления ОТК. Пренебрежение уровнями Ландау может привести к неверным результатам, особенно в сильных магнитных полях или при низких температурах, где квантовые эффекты становятся доминирующими.

Центр Вращения: Находим Удобный Угол Обзора

Использование координат центра вращения, описывающих центр циклотронного движения, представляет собой естественный подход к анализу систем в магнитных полях. Вместо отслеживания траектории отдельной частицы, координаты центра вращения фокусируются на эволюции положения этого центра, что упрощает описание движения в неоднородных магнитных полях. Эти координаты позволяют отделить быстрое циклотронное вращение от медленного дрейфа, вызванного градиентами магнитного поля или внешними силами. Такой подход особенно полезен при анализе плазмы и других систем, где частицы испытывают сильные магнитные поля, поскольку он позволяет эффективно описывать коллективное поведение частиц и их транспортные свойства. \mathbf{R} = \mathbf{r} - \frac{\mathbf{v}_{\perp}}{B} \times \mathbf{B} , где \mathbf{R} — координата центра вращения, \mathbf{r} — положение частицы, \mathbf{v}_{\perp} — перпендикулярная компонента скорости, а \mathbf{B} — магнитное поле.

Построение ОТК (Оператора Временной Эволюции) с использованием координат направляющего центра — так называемый ОТК направляющего центра — существенно упрощает вычисления в системах с магнитными полями. Применение этих координат позволяет отслеживать движение центра циклотронного вращения, что снижает вычислительную сложность при анализе динамики частиц. В частности, такой подход позволяет более эффективно рассчитывать влияние неоднородных потенциалов на движение частиц, выделяя ключевые физические эффекты, связанные с эффективной семиклассической динамикой направляющих центров. ОТК направляющего центра предоставляет естественный инструмент для анализа временной эволюции операторов и позволяет более четко интерпретировать полученные результаты.

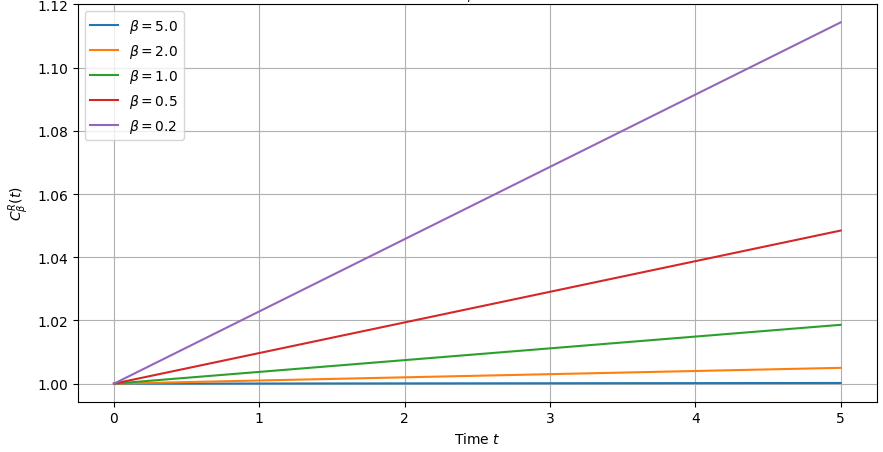
Использование координат ведущего центра позволяет анализировать динамику частиц в магнитных полях. Исследования показывают, что тепловой рост OTOC (Out-of-Time-Ordered Correlation) линейный по времени, что указывает на эффективную семиклассическую динамику ведущих центров в неоднородном потенциале. Этот результат демонстрирует, что динамика частиц, описываемая координатами ведущего центра, приближается к классической, особенно в условиях неоднородного магнитного поля. \frac{d}{dt} OTOC \propto t — такое поведение подтверждает, что OTOC растет пропорционально времени, что отличает его от экспоненциального роста, характерного для полностью квантовых систем. Данный подход позволяет изучать связь между квантовой и классической динамикой в сложных магнитных конфигурациях.

Подавление экспоненциального роста Guiding-center OTOC (Out-of-Time-Ordered Correlation) указывает на фильтрацию быстрого циклотронного движения. Этот эффект проявляется в снижении скорости квантового перемешивания (quantum scrambling) в системе. Анализ OTOC демонстрирует, что высокочастотные колебания, связанные с циклотронным движением, эффективно подавляются при использовании координат ведущего центра, что приводит к ослаблению связи между начальными и конечными степенями свободы. В результате, динамика системы описывается преимущественно медленными степенями свободы, а квантовое перемешивание становится менее эффективным, что проявляется в более низкой скорости роста OTOC по сравнению с системами, где циклотронное движение не фильтруется.

Измеряя Хаос: Показатель Ляпунова и Перемешивание Информации

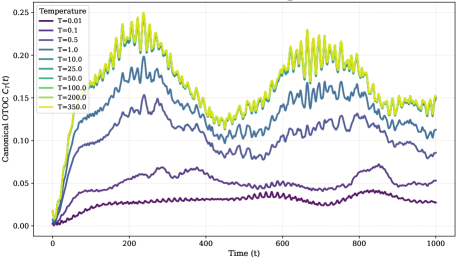
Расчеты OTOC (Out-of-Time-Ordered Correlations) позволяют выделить ключевую характеристику хаотических систем — показатель Ляпунова. Данный показатель напрямую измеряет скорость расхождения траекторий, изначально находящихся вблизи друг от друга. По сути, он количественно оценивает, насколько быстро небольшие различия в начальных условиях приводят к экспоненциально растущему отклонению в поведении системы. Чем больше положительное значение показателя Ляпунова, тем быстрее происходит это расхождение и тем более хаотичной является система. Таким образом, показатель Ляпунова служит надежным индикатором хаотичности и позволяет сравнивать степень хаоса в различных системах, предоставляя количественную меру их чувствительности к начальным условиям.

Положительное значение показателя Ляпунова является не только подтверждением наличия хаоса в системе, но и точным измерением скорости, с которой информация рассеивается и перераспределяется внутри неё. Этот показатель количественно определяет, насколько быстро две изначально близкие траектории в фазовом пространстве расходятся, что фактически отражает скорость «перемешивания» системы. Чем выше показатель Ляпунова, тем быстрее происходит это рассеяние информации, и тем сложнее предсказать поведение системы в долгосрочной перспективе. Таким образом, показатель Ляпунова предоставляет ключевой инструмент для характеристики степени хаотичности и оценки скорости распространения информации в сложных динамических системах, от бильярдов с магнитными полями до квантовых систем.

Исследование демонстрирует, что применение поперечного магнитного поля позволяет модулировать квантический хаос в бильярдных системах. Это приводит к наблюдаемому взаимодействию между хаотическим поведением, обусловленным границами, и динамикой, ограничиваемой магнитным полем. В рамках данной работы был идентифицирован показатель, аналогичный показателю Ляпунова, который характеризует скорость роста квантового перемешивания на ранних стадиях. Этот показатель позволяет количественно оценить, насколько быстро информация распространяется и «перемешивается» внутри системы, открывая новые возможности для управления и изучения квантического хаоса.

Исследования показали, что показатель Ляпунова, характеризующий скорость расхождения близких траекторий в хаотической системе, не является постоянной величиной. Он демонстрирует зависимость от температуры и величины приложенного магнитного поля. При низких значениях магнитного поля наблюдается неустойчивый, хаотический рост, что указывает на быстрое распространение информации по системе. Однако, с увеличением магнитного поля, данный рост подавляется, свидетельствуя о переходе к более упорядоченному режиму динамики. Таким образом, магнитное поле выступает в роли управляющего параметра, позволяющего настраивать степень хаотичности и контролировать скорость информационного перемешивания в системе, что открывает возможности для изучения и управления квантическими процессами.

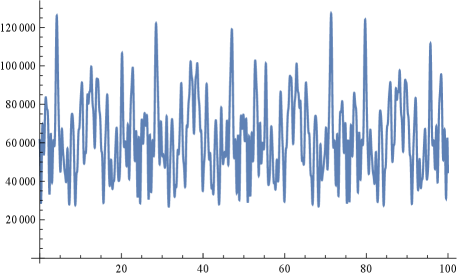
Исследование демонстрирует, как магнитные поля влияют на хаотичность квантовых систем, словно приручая беспорядок. Авторы показывают, что управляя этими полями, можно контролировать скорость ‘перемешивания’ информации — процесс, известный как термиализация. Этот контроль напоминает попытку уговорить хаос, заставить его двигаться в нужном направлении. Как говорил Юрген Хабермас: «Коммуникативное действие — это попытка достичь взаимопонимания, основанная на аргументах и рациональном обсуждении». В данном исследовании магнитное поле — это своего рода аргумент, обращенный к хаотической системе, стремящийся направить её поведение. Иногда, когда данные выглядят слишком упорядоченно, возникает ощущение, что модель лжёт красиво — это особенно заметно в контексте хаотических систем, где даже малейшее отклонение может привести к непредсказуемым последствиям.

Куда же всё это ведёт?

Представленные здесь игры с магнитными полями и хаосом в квантовых счетах — лишь проблеск, мимолётное отражение той неуловимой закономерности, что прячется в шепоте случайности. Попытки обуздать хаос, заставить его плясать под нашу дудку, неизбежно сталкиваются с границами применимости любой модели. Помните, каждое заклинание имеет свою цену, и каждая попытка контроля порождает новые, непредсказуемые возмущения. Вопрос не в том, чтобы подавить хаос, а в том, чтобы научиться читать его знаки, понимать его язык.

Особенно интригующим представляется связь между движением в направляющих центрах и подавлением хаотичности. Это намекает на существование скрытых степеней свободы, которые могут быть использованы для тонкой настройки динамики квантового перемешивания. Однако, предстоит выяснить, насколько универсален этот механизм, и применим ли он к более сложным системам, где взаимодействие между частицами становится более запутанным. Следует обратить внимание на системы с большим числом частиц, где коллективные эффекты могут кардинально изменить картину поведения.

В конечном итоге, исследование квантового хаоса — это не столько поиск ответов, сколько постановка всё более сложных и изощрённых вопросов. Данные — всего лишь тени на стене пещеры, а истина, возможно, лежит за пределами любой математической формулы. И пусть попытки её постичь будут обречены на провал, сам процесс поиска — вот что действительно имеет значение. Потому что даже в хаосе есть своя красота, своя завораживающая логика.

---

Оригинал статьи: https://arxiv.org/pdf/2602.05322.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

• Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.

• Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip

• Все рецепты культистского круга в Escape from Tarkov

• Нечестивцам нет покоя: как получить старый ключ от коттеджа

• Решение головоломки с паролем Absolum в Yeldrim.

• Прогнозы криптовалюты AXS: информация о ценах на AXS

• Arknights: Endfield — Интерактивная карта (Долина IV)

• Акции UGLD. Южуралзолото ГК: прогноз акций.

• Лучшие шаблоны дивизий в Hearts Of Iron 4

• Кто такая Кселия Мендес-Джонс? 5 вещей, которые нужно знать об актере Fallout

2026-02-06 23:17