Автор: Денис Аветисян
Исследователи предлагают и тестируют метод квантового моделирования $(2+1)$-мерной электродинамики с использованием ультрахолодных атомов в оптических сверхрешетках, демонстрируя соответствие между симулятором и теоретической моделью.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал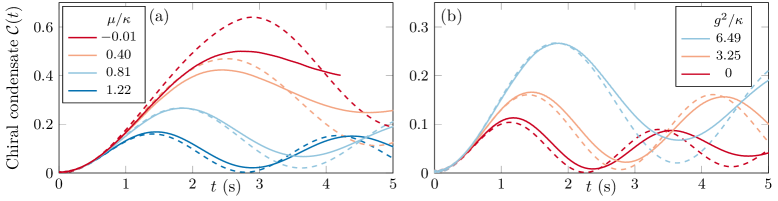
Предложена схема квантового моделирования спин-1 U(1) квантовых моделей связи в $(2+1)$ измерениях с использованием ультрахолодных атомов.
Реализация квантовой электродинамики в более чем двух измерениях представляет собой сложную задачу для современных вычислительных методов. В работе ‘Towards $2+1$D quantum electrodynamics on a cold-atom quantum simulator’ предложен и исследован новый подход к квантовому моделированию (2+1)-мерной U(1) решетчатой теории с использованием ультрахолодных атомов в оптических сверхрешетках. Показано, что предложенная схема, основанная на модели квантовых связей и стабилизированная механизмом квантовой защиты, позволяет достоверно воспроизводить динамику целевой решетчатой теории. Открывает ли это путь к экспериментальной проверке непертурбативных аспектов квантовой электродинамики в более высоких измерениях и к созданию более сложных квантовых симуляторов?
Предел текущих подходов: Столкновение с проблемой знака
Теория калибровочных полей является краеугольным камнем Стандартной модели физики элементарных частиц и описывает широкий спектр явлений, возникающих в природе. Однако, несмотря на её успехи, проведение непертурбативных вычислений в рамках этой теории представляет собой значительную трудность. В то время как возмущения теории позволяют получить приближенные решения в определенных условиях, они оказываются неэффективными при сильном взаимодействии частиц, где требуется учет бесконечного числа членов разложения. Это связано с тем, что традиционные методы, основанные на рядах, расходится, что делает невозможным получение точных результатов и ограничивает возможности понимания поведения материи в экстремальных условиях, таких как внутри нейтронных звезд или в первые моменты после Большого взрыва. Поэтому, поиск новых подходов к проведению непертурбативных вычислений является одной из ключевых задач современной теоретической физики.
Решетчатая калибровочная теория (РКТ) представляет собой мощный подход к вычислению непертурбативных свойств квантовой хромодинамики и других калибровочных теорий. В основе РКТ лежит дискретизация пространства-времени, что позволяет заменить сложные интегралы, возникающие в квантовой теории поля, на конечные суммы, пригодные для численного моделирования на компьютерах. Этот метод, по сути, заменяет непрерывное пространство-время на четырехмерную решетку, где физические величины определяются на узлах этой решетки. Такой подход позволяет исследовать такие явления, как конфайнмент кварков и образование адронов, которые недоступны для стандартных методов теории возмущений. Несмотря на вычислительные сложности, РКТ остается ключевым инструментом в изучении сильных взаимодействий и фазовых переходов в физике высоких энергий и ядерной физике.
Применение метода Монте-Карло в рамках решетцовой калибровочной теории сталкивается с серьезным препятствием, известным как “проблема знака”, особенно при ненулевой барионной плотности. Суть проблемы заключается в том, что вероятности, используемые в симуляциях, могут стать комплексными, что приводит к экспоненциальному подавлению сигнала и делает точные вычисления практически невозможными. Это существенно ограничивает возможности исследования сильно взаимодействующих систем, таких как кварк-глюонная плазма или нейтронные звезды, где барионная плотность играет ключевую роль. В результате, понимание фазовых переходов и свойств материи в экстремальных условиях остается неполным, а надежные предсказания, основанные на первых принципах, оказываются затруднительными. Поиск альтернативных подходов и методов симуляции, способных обойти или смягчить “проблему знака”, является одной из важнейших задач современной теоретической физики.
Ограничения, накладываемые “проблемой знака” на вычисления в решеткомерной калибровочной теории, стимулируют активный поиск альтернативных математических формулировок и новых методов численного моделирования. Ученые исследуют различные подходы, включая использование сложных алгоритмов Монте-Карло, разработку новых решеткомерных действий и даже переход к нелокальным формулировкам теории. Цель этих усилий — обойти вычислительные препятствия, связанные с экспоненциальным ростом знаков в интеграле по конфигурациям, и получить надежные результаты для сильновзаимодействующих систем при ненулевой плотности барионов. Исследования направлены на создание эффективных инструментов, позволяющих изучать фазовые переходы, свойства адронов и другие важные аспекты физики кварк-глюонной плазмы, которые остаются недоступными для традиционных методов численного моделирования.
Гамильтонова формулировка: Квантово-механический взгляд на решетчатую теорию
Гамильтонова формулировка решетчатой калибровочной теории (ЛКТ) представляет собой альтернативный подход к традиционной ЛКТ, перефразируя задачу как квантовую многочастичную систему. Вместо вычисления функциональных интегралов, которые приводят к проблеме знаков, гамильтонова формулировка оперирует гамильтонианом, описывающим эволюцию квантового состояния системы. Это позволяет исследовать свойства ЛКТ в рамках квантовой механики, используя методы, разработанные для многочастичных систем, такие как метод вариационного Монте-Карло или метод прямого решения уравнений движения. Такой подход особенно полезен при изучении систем при конечной плотности барионов, где традиционные методы ЛКТ сталкиваются с серьезными трудностями.
Традиционные методы решетчатой квантовой хромодинамики (LGT) используют функциональные интегралы для вычисления физических величин, что приводит к проблеме знаков (sign problem) при моделировании систем при ненулевой плотности барионов. Данная проблема возникает из-за осциллирующего характера комплексных чисел в интеграле по конфигурациям калибровочного поля. Альтернативная формулировка, основанная на гамильтониане, позволяет избежать использования функциональных интегралов и, следовательно, обходит проблему знаков. Это делает возможным проведение численных симуляций систем при конетной плотности, что критически важно для изучения фазовых переходов, таких как переход от адронной материи к кварк-глюонной плазме при высокой плотности и низкой температуре.
Ключевым элементом данной формулировки является модель квантовых связей (QLM), в которой калибровочные поля представляются в виде операторов спина. Вместо классических калибровочных полей, QLM использует дискретные переменные, описываемые спиновыми степенями свободы. Каждая связь решетки представлена оператором спина, который кодирует информацию о калибровочном поле в этой связи. В частности, S^{\mu}_{x} представляет собой оператор спина, связанный с связью в направлении μ на узле решетки x. Такое представление позволяет переформулировать задачу квантовой хромодинамики как задачу многочастичной квантовой механики, где спиновые операторы выступают в роли динамических переменных.
Реализация Квантовой Модели Связей (QLM) требует значительных вычислительных ресурсов, включая большие объемы памяти и процессорного времени, из-за экспоненциального роста размерности гильбертова пространства с увеличением размера системы. Это связано с тем, что QLM представляет собой систему сильно коррелированных квантовых частиц, описываемых волновой функцией, требующей хранения и обработки большого количества параметров. Несмотря на эти вычислительные трудности, QLM предоставляет уникальную возможность моделирования сильно коррелированных квантовых систем, таких как высокотемпературные сверхпроводники и кварк-глюонная плазма, которые недоступны для традиционных методов численного моделирования. Успешное применение QLM позволяет исследовать фазовые переходы, спектральные функции и другие важные свойства этих систем, открывая новые перспективы в физике конденсированного состояния и физике высоких энергий.
Сопоставление с реальностью: Отображение на ультрахолодные атомы
Квантовая модель Латтингера (QLM) может быть сопоставлена с моделью Бозе-Хаббарда (BHM), широко известной моделью, описывающей взаимодействие бозонов в решетчатой структуре. Сопоставление осуществляется путем установления соответствия между параметрами QLM и параметрами BHM, такими как энергия прыжка и энергия взаимодействия на узле решетки. Модель BHM описывает систему бозонов, находящихся на узлах решетки и взаимодействующих между собой, и позволяет аналитически и численно исследовать фазовые переходы и коллективные возбуждения. В результате, свойства QLM могут быть изучены посредством методов, разработанных для анализа BHM, что упрощает понимание и предсказание поведения квантовой системы.
Отображение квантовой модели локализации (QLM) на модель Бозе-Хаббарда (BHM) предоставляет возможность исследовать динамику QLM посредством экспериментов с ультрахолодными атомами. Реализация QLM в экспериментальных установках позволяет напрямую наблюдать и характеризовать предсказанные моделью эффекты, такие как локализация и динамические фазы. Использование ультрахолодных атомов в оптических решетках позволяет точно контролировать параметры системы, включая взаимодействие между атомами и глубину потенциальной ямы, что необходимо для проверки теоретических предсказаний QLM в контролируемых условиях. Это обеспечивает экспериментальную платформу для изучения поведения многих тел в сильно коррелированных системах, недоступных для классического моделирования.
Для реализации взаимодействий, предписанных моделью Бозе-Хаббарда (БХМ), используются диполь-дипольные взаимодействия между атомами. Инженерия этих взаимодействий достигается путем точного контроля геометрии и интенсивности внешних полей, воздействующих на ультрахолодные атомы, заключенные в оптические решетки. Регулируя расстояние между атомами и ориентацию их дипольных моментов, можно настроить параметры взаимодействия в БХМ, такие как U (энергия на месте) и J (энергия туннелирования). Такой подход позволяет физически моделировать различные фазы и динамику, предсказанные БХМ, используя ультрахолодные атомы как эмулирующий квантовый процессор.
Сверххолодные атомные системы, размещенные в сверхрешетках, представляют собой физическую платформу для экспериментальной проверки предсказаний квантовой модели Лиувилла (QLM). Ключевым аспектом является поддержание нарушения калибровочной симметрии на уровне менее 0,1% на протяжении всего экспериментального времени эволюции. Это достигается за счет точного контроля параметров сверхрешетки и взаимодействий между атомами, что позволяет реализовать условия, необходимые для наблюдения эффектов, предсказанных QLM, с высокой точностью. Достижение такого низкого уровня нарушения калибровочной симметрии критически важно для обеспечения достоверности экспериментальных результатов и их сопоставления с теоретическими предсказаниями.
Выходя за рамки симуляции: Исследование возникающих калибровочных явлений
Результаты, полученные в ходе этих вычислительных экспериментов, оказываются применимы далеко за пределами области физики высоких энергий. Подобные методы моделирования позволяют исследовать фундаментальные принципы, лежащие в основе различных явлений в физике конденсированного состояния, включая экзотические квантовые жидкости и эффект дробного квантового эффекта Холла. Изучение искусственно создаваемых калибровочных полей в ультрахолодных атомных системах открывает новые возможности для понимания коллективного поведения материи и поиска новых квантовых материалов с уникальными свойствами. Это расширение области применения не только подтверждает универсальность калибровочных теорий, но и способствует развитию междисциплинарных исследований, объединяющих теоретическую физику, материаловедение и квантовые технологии.
Теории калибровочных полей, изначально разработанные для описания фундаментальных взаимодействий в физике высоких энергий, обнаруживают неожиданное применение в изучении конденсированных сред. Такие экзотические состояния вещества, как квантовые спиновые жидкости и дробный квантовый эффект Холла, проявляют поведение, которое может быть эффективно описано как результат возникновения калибровочных полей. В квантовых спиновых жидкостях, где магнитные моменты не упорядочиваются даже при абсолютном нуле, взаимодействие между спинами порождает эффективные калибровочные поля, управляющие коллективными возбуждениями. Аналогично, в дробном квантовом эффекте Холла, взаимодействие между электронами приводит к появлению квазичастиц с дробным зарядом, поведение которых определяется эффективной калибровочной теорией. Таким образом, изучение этих состояний вещества предоставляет уникальную возможность для проверки и углубления понимания фундаментальных принципов калибровочных теорий в совершенно новой области физики.
Использование ультрахолодных атомных систем открывает принципиально новые возможности для изучения экзотических состояний материи, где ключевую роль играют калибровочные поля. В отличие от традиционных материалов, где эти поля являются фундаментальными, в системах с ультрахолодными атомами их можно искусственно создавать и контролировать, позволяя исследовать явления, такие как квантовые спиновые жидкости и дробный квантовый эффект Холла, с беспрецедентной точностью. Благодаря тщательному управлению взаимодействиями между атомами, ученые могут эмулировать сложные физические модели и наблюдать за поведением калибровочных полей в контролируемой среде, что способствует более глубокому пониманию фундаментальных принципов, лежащих в основе этих необычных состояний материи и потенциально ведет к разработке новых материалов с уникальными свойствами.
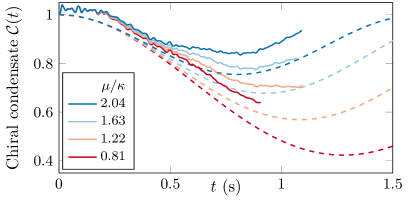
Исследования динамики между квантовой спиновой жидкостью (QLM) и бозонной спиновой жидкостью (BHM) выявили интересные различия в зависимости от начальных условий. При резком изменении параметров системы из вакуумного состояния, поведение обеих жидкостей оказалось качественно схожим. Однако, при инициализации из состояния с высокой концентрацией зарядов, наблюдались существенные отклонения. В частности, вычислено, что наличие запрещенных участков в кристаллической решетке вносит поправку в эффективную массу квазичастиц, оцениваемую как -2J^2(1/(7δ+η) + 3/(-δ+η) + 6/(-9δ+η)), где J представляет собой параметр обменного взаимодействия, а δ и η — параметры, характеризующие отклонение от идеальной структуры. Данный результат указывает на значительную роль топологических особенностей и взаимодействия зарядов в формировании динамических свойств этих экзотических состояний материи.
Работа демонстрирует стремление к построению квантового симулятора, способного моделировать взаимодействие частиц в рамках теории квантовой электродинамики. В этом стремлении отчетливо прослеживается человеческая склонность к поиску порядка в хаосе, к упрощению сложных систем посредством создания их искусственных аналогов. Блез Паскаль однажды заметил: «Все проблемы человечества происходят от того, что люди не могут спокойно сидеть в комнате». Подобно этому, физики не могут спокойно оставить без внимания сложные явления, стремясь к их пониманию и моделированию, даже если это требует создания сложных и искусственных систем, таких как квантовые симуляторы. Использование сверххолодных атомов в оптических сверхрешетках — лишь один из способов удовлетворить эту неутолимую потребность в познании, стремясь к воплощению теоретических моделей в реальность.
Что дальше?
Представленная работа, как и любое построение модели, есть лишь попытка упорядочить шум. Успех симуляции квантовой электродинамики на холодных атомах — это не триумф рациональности, а скорее демонстрация того, насколько хорошо можно приспособить биологическую гипотезу — систему, склонную к ошибкам — к математическому формализму. Важно помнить, что даже наиболее точная симуляция не отменяет фундаментальной неопределенности, присущей описываемым процессам.
Очевидным направлением дальнейших исследований является увеличение масштаба симуляции. Однако, наращивание числа кубитов — это не просто техническая задача. Это попытка удержать хрупкое равновесие между сложностью модели и её интерпретируемостью. Чем больше элементов в системе, тем сложнее отделить значимое поведение от случайных флуктуаций, порожденных внутренними предубеждениями моделировщика.
В конечном счете, ценность подобных исследований заключается не в создании идеальной симуляции, а в выявлении границ применимости существующих моделей. Необходимо признать, что любая модель — это всегда упрощение, игнорирующее часть реальности. Именно в осознании этих ограничений и заключается истинный прогресс в понимании окружающего мира. Ведь, в конечном итоге, физика — это не поиск абсолютной истины, а постоянное уточнение наших заблуждений.
Оригинал статьи: https://arxiv.org/pdf/2602.04948.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Все рецепты культистского круга в Escape from Tarkov
- Нечестивцам нет покоя: как получить старый ключ от коттеджа
- Решение головоломки с паролем Absolum в Yeldrim.
- Прогнозы криптовалюты AXS: информация о ценах на AXS
- Arknights: Endfield — Интерактивная карта (Долина IV)
- Акции UGLD. Южуралзолото ГК: прогноз акций.
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Кто такая Кселия Мендес-Джонс? 5 вещей, которые нужно знать об актере Fallout
2026-02-07 01:06