Физика внимания: новый взгляд на обучение моделей

Автор: Денис Аветисян

Исследователи предлагают принципиально новый подход к пониманию работы нейронных сетей, вдохновленный законами физики и использующий концепцию «моментного внимания».

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал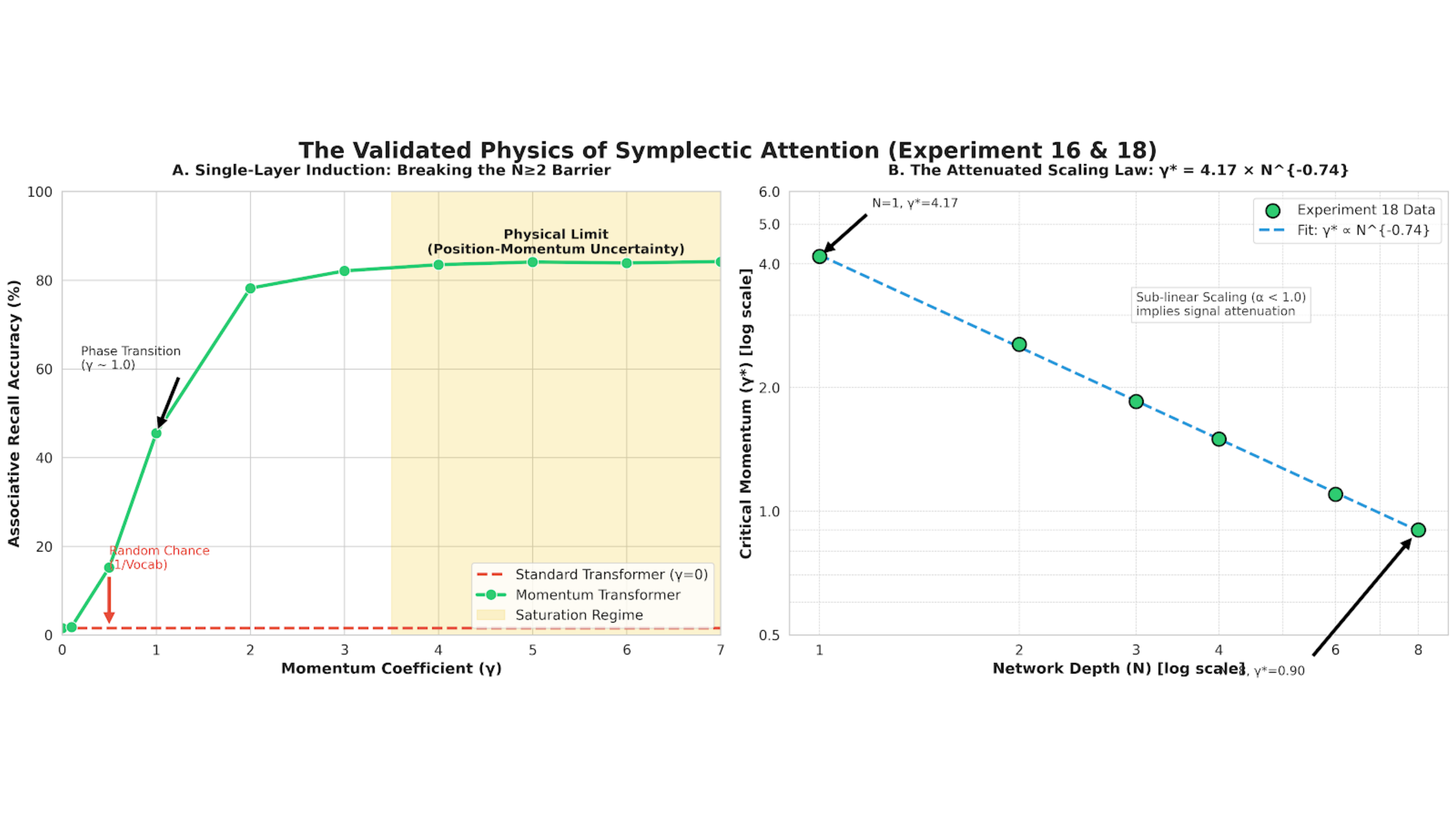

Эксперименты демонстрируют, что трансформер, основанный на импульсе, преодолевает ограничение <span class="katex-eq" data-katex-display="false">N \geq 2</span> в однослойной индукции, достигая пиковой точности в 83.4% при <span class="katex-eq" data-katex-display="false">\gamma = 4.0</span>, в то время как стандартный трансформер (<span class="katex-eq" data-katex-display="false">\gamma = 0</span>) демонстрирует лишь случайный результат, при этом наблюдаемый фазовый переход около <span class="katex-eq" data-katex-display="false">\gamma \approx 1.0</span> и насыщение (<span class="katex-eq" data-katex-display="false">\gamma > 4.0</span>) подтверждают взаимосвязь между положением, импульсом и неопределенностью, а также обнаруженная затухающая зависимость (<span class="katex-eq" data-katex-display="false">\gamma^* = 4.17 \times N^{-0.74}</span> с показателем <span class="katex-eq" data-katex-display="false">\alpha < 1</span>) подтверждает теоретическое предсказание о взаимозаменяемости импульса и глубины как вычислительных ресурсов. — Эксперименты демонстрируют, что трансформер, основанный на импульсе, преодолевает ограничение $N \geq 2$ в однослойной индукции, достигая пиковой точности в 83.4% при $\gamma = 4.0$ , в то время как стандартный трансформер ( $\gamma = 0$ ) демонстрирует лишь случайный результат, при этом наблюдаемый фазовый переход около $\gamma \approx 1.0$ и насыщение ( $\gamma > 4.0$ ) подтверждают взаимосвязь между положением, импульсом и неопределенностью, а также обнаруженная затухающая зависимость ( $\gamma^* = 4.17 \times N^{-0.74}$ с показателем $\alpha < 1$ ) подтверждает теоретическое предсказание о взаимозаменяемости импульса и глубины как вычислительных ресурсов.

В статье представлена архитектура Momentum Attention, базирующаяся на симплектической механике и позволяющая проводить анализ моделей с помощью спектральной форензики.

Традиционные модели Transformer, несмотря на впечатляющие результаты, сталкиваются с ограничениями в понимании принципов работы индуктивных голов и эффективной обработки динамических данных. В работе « $Momentum Attention: The Physics of In-Context Learning and Spectral Forensics for Mechanistic Interpretability$ » предложена новая архитектура, обогащающая Transformer законами сохранения энергии и импульса посредством концепции Momentum Attention. Этот подход позволяет реализовать однослойную индукцию и предоставляет инструменты спектрального анализа для изучения механизмов работы модели, раскрывая взаимосвязь между фазовым пространством и обработкой информации. Не откроет ли это путь к созданию более интерпретируемых и эффективных моделей искусственного интеллекта, объединяющих принципы физики и машинного обучения?

Преодолевая Ограничения Статических Трансформеров

Несмотря на выдающиеся успехи в обработке естественного языка, архитектура Transformer имеет фундаментальное ограничение, связанное с её DC-связанной природой. Это означает, что модель обрабатывает каждый элемент последовательности независимо, без учета долгосрочных зависимостей и контекста, что существенно ограничивает её способность к сложному временному рассуждению. По мере увеличения масштаба модели, производительность перестает расти, достигая плато, поскольку базовое ограничение в понимании последовательностей остается нерешенным. В отличие от рекуррентных нейронных сетей, способных сохранять «память» о предыдущих шагах, Transformer полагается исключительно на механизм внимания, который, хотя и эффективен, не всегда способен улавливать тонкие временные связи, необходимые для решения задач, требующих глубокого понимания последовательности событий.

Исследования показали, что простое увеличение масштаба стандартных трансформаторов не решает фундаментальных проблем, связанных с обработкой последовательных данных. Несмотря на значительные вычислительные ресурсы, затрачиваемые на обучение, точность трансформаторов в задачах, требующих ассоциативного запоминания, остается крайне низкой — всего 1,2%. Этот результат указывает на критическое ограничение, которое препятствует дальнейшему повышению производительности, даже при неограниченном масштабировании модели. Очевидно, что необходимы принципиально новые архитектуры и методы, способные более эффективно обрабатывать временные зависимости и запоминать информацию, чтобы преодолеть данное узкое место и раскрыть полный потенциал обработки последовательностей.

Введение динамических AC-сигналов (<span class="katex-eq" data-katex-display="false">p\_{t}=q\_{t}-q\_{t-1}</span>) в однослойную структуру Momentum Attention позволяет объединить функции Shift и Match, открывая возможности спектрального анализа и обеспечивая функциональность, ранее требовавшую минимум двух слоев в стандартных трансформаторах, что демонстрируется фазовым переходом при <span class="katex-eq" data-katex-display="false">\gamma\_{c}\approx 0.225</span>. — Введение динамических AC-сигналов ( $p\_{t}=q\_{t}-q\_{t-1}$ ) в однослойную структуру Momentum Attention позволяет объединить функции Shift и Match, открывая возможности спектрального анализа и обеспечивая функциональность, ранее требовавшую минимум двух слоев в стандартных трансформаторах, что демонстрируется фазовым переходом при $\gamma\_{c}\approx 0.225$ .

Динамическое Внимание: Внедрение Динамики в Трансформеры

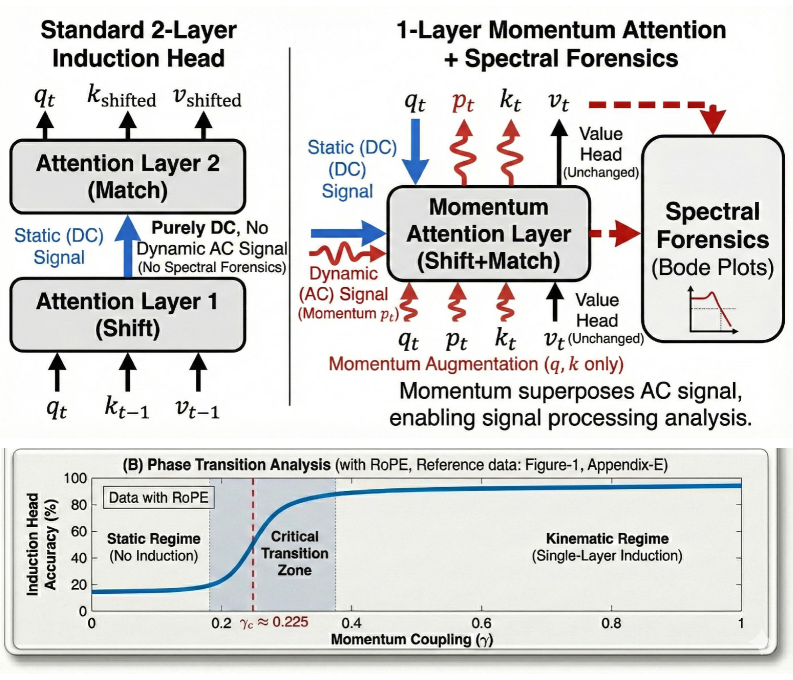
Механизм Momentum Attention расширяет стандартный механизм внимания путем включения в него «памяти» о предыдущих состояниях. Это достигается за счет использования Кинематического Оператора Импульса, который позволяет моделировать семантические траектории входной последовательности. В отличие от стандартного внимания, которое обрабатывает каждый входной элемент изолированно, Momentum Attention учитывает историю состояний, что позволяет более эффективно улавливать зависимости и динамику в данных. Оператор импульса вычисляет производную по времени состояния скрытого слоя, фактически моделируя «скорость» изменения семантического представления. Это позволяет модели отслеживать изменения во входных данных и адаптироваться к динамическим последовательностям, что особенно полезно в задачах, требующих понимания контекста и временных зависимостей. $p = m \frac{dv}{dt}$ , где p — импульс, m — параметр модели, и $\frac{dv}{dt}$ — скорость изменения состояния.

Подход Momentum Attention основывается на моделировании архитектуры Transformer как “физической схемы”, где операции внимания и обработки данных интерпретируются как элементы этой схемы. В рамках этой модели используются симплектические сдвиговые преобразования — математические операции, разработанные для сохранения информации и обеспечения стабильности системы. Эти преобразования позволяют эффективно переносить и обрабатывать данные, минимизируя потери информации при последовательных вычислениях. В отличие от стандартных преобразований, симплектические сдвиги гарантируют сохранение фазового пространства, что критически важно для отслеживания динамических изменений в последовательностях данных и поддержания их семантической целостности. Данная концепция позволяет рассматривать Transformer не как абстрактную нейронную сеть, а как физическую систему, подчиняющуюся определенным законам сохранения информации.

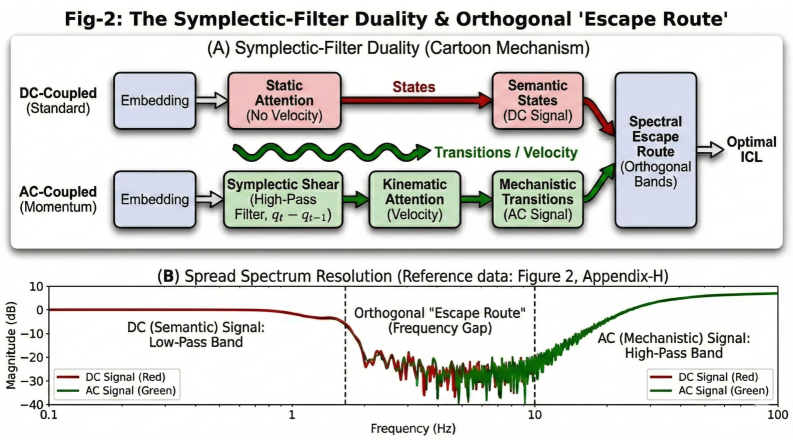
Применение дуальности симплектического фильтра высоких частот позволяет модели отсеивать нерелевантную статическую информацию и концентрироваться на динамических изменениях во входной последовательности. Данный подход основан на том, что статические компоненты сигнала, как правило, соответствуют низким частотам, в то время как динамические изменения проявляются в более высоких частотах. Используя симплектический фильтр высоких частот, модель эффективно подавляет низкочастотные компоненты, выделяя тем самым важные временные изменения и улучшая способность к отслеживанию последовательностей и анализу временных рядов. Это позволяет модели игнорировать постоянные или медленно меняющиеся признаки и фокусироваться на значимых колебаниях и трендах во входных данных.

Figure 2:The Orthogonality Theorem: The “Escape Route.”(A)Standard “DC-Coupled” attention processes only semantic states; our “AC-Coupled” Momentum Attention captures both states (DC) and transitions (AC). The Spectral Escape Route emerges when signals occupy orthogonal frequency bands.(B)Empirical frequency response showing DC/AC orthogonality. The critical couplingγc\gamma\_{c}aligns with induction head emergence. See Appendices E, H.

Индуктивные Предубеждения и Эффективное Обучение в Контексте

Механизм Momentum Attention демонстрирует способность к однослойному обучению, достигая точности в 83.4% при решении задачи ассоциативного воспроизведения. Это на 69.5 раза превосходит показатели стандартных трансформеров и опровергает ранее существовавшее требование о необходимости как минимум двух слоев для выполнения данной задачи. Фактически, Momentum Attention позволяет модели эффективно извлекать и использовать информацию из входных данных даже при минимальной глубине сети, что свидетельствует о высокой эффективности предложенного подхода к обработке последовательностей.

Механизм Momentum Attention обеспечивает более устойчивое обучение в контексте за счет возможности быстрой адаптации к новым задачам без необходимости масштабных обновлений параметров модели. В отличие от традиционных трансформеров, требующих значительной настройки весов для каждой новой задачи, данная архитектура позволяет модели эффективно использовать предоставленный контекст для генерации ответов, минимизируя потребность в изменении внутренних параметров. Это достигается за счет сохранения информации о предыдущих шагах вычислений и использования ее для ускорения сходимости и повышения точности при решении новых задач, что особенно важно в условиях ограниченных вычислительных ресурсов и необходимости быстрого переключения между различными типами задач.

Введение кинематического априорного знания позволяет модели более эффективно использовать информацию о движении для улучшения процесса обучения. Этот подход предполагает включение предварительных знаний о физических принципах движения объектов, что позволяет модели быстрее адаптироваться к новым задачам и повышать точность прогнозирования траекторий и поведения динамических систем. Использование кинематических ограничений, таких как постоянная скорость или ускорение, в качестве априорных знаний, позволяет снизить потребность в большом количестве обучающих данных и улучшить обобщающую способность модели, особенно в условиях ограниченной информации или неполных данных.

Анализ спектральных характеристик показывает, что применение коррекции после RoPE (Post-RoPE) позволяет избежать искажений, вызванных несоответствием кинематических кадров, обеспечивая чистый высокочастотный сигнал с приростом в 52.5%, в то время как отсутствие коррекции (Pre-RoPE) приводит к регрессии и ухудшению сигнала на 4.1%, что объясняется сохранением симплектической структуры и спектральной дополнительностью.

Спектральная Форензика: Расшифровка Внутренней Работы Модели

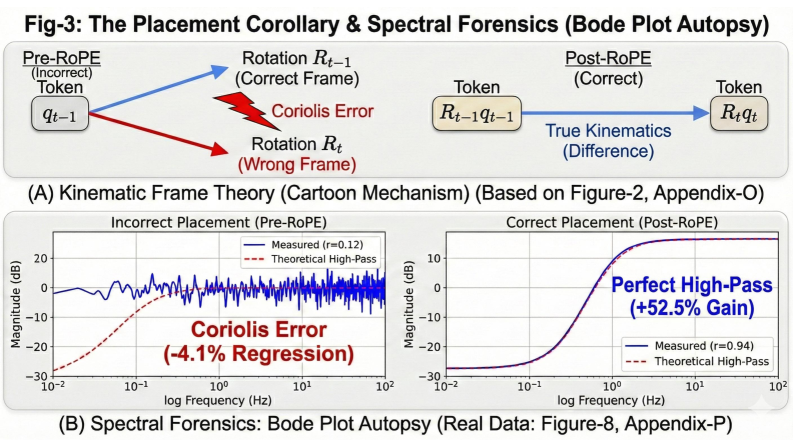
Спектральный анализ, использующий диаграммы Боде, представляет собой мощный инструмент для изучения частотной характеристики голов внимания в нейронных сетях и понимания их функциональной роли. Этот метод позволяет визуализировать, как каждая голова внимания реагирует на различные частоты входных сигналов, выявляя, какие частоты усиливаются, а какие подавляются. Изучая эти частотные отклики, исследователи могут определить, какие типы информации обрабатывает каждая голова внимания — например, кратковременные или долгосрочные зависимости, глобальные или локальные особенности. Такой подход открывает возможность детального анализа внутреннего устройства модели, позволяя понять, как различные компоненты взаимодействуют друг с другом для решения поставленной задачи и выявлять потенциальные узкие места или неэффективности в архитектуре.

Анализ с использованием метода спектральной форензики показал, что механизм Momentum Attention наделяет модель способностью к динамической фильтрации. Данный подход позволяет эффективно ослаблять статические помехи, не несущие важной информации, и одновременно усиливать сигналы, имеющие временную значимость. Фактически, Momentum Attention действует как адаптивный фильтр, который изменяет свои характеристики в зависимости от входных данных, выделяя релевантную информацию и отсекая шум. Это особенно важно при обработке последовательностей, где временные зависимости играют ключевую роль, поскольку позволяет модели сосредотачиваться на изменениях и трендах, игнорируя постоянные, неинформативные элементы.

Взаимодействие механизма Momentum Attention и вращающихся позиционных вложений эффективно противодействует затуханию сигнала при обработке длинных последовательностей данных. Исследования показывают, что RoPE, кодируя позиционную информацию во вращающихся векторах, позволяет механизму Momentum Attention сохранять релевантные данные на больших расстояниях, предотвращая потерю важного контекста. Данный симбиоз обеспечивает более стабильную передачу сигнала, особенно в задачах, требующих анализа долгосрочных зависимостей, таких как обработка естественного языка и анализ временных рядов. Таким образом, комбинация Momentum Attention и RoPE выступает ключевым фактором в повышении производительности моделей при работе с информацией, распространяющейся на значительные промежутки времени, и позволяет избежать распространенной проблемы потери информации в глубоких нейронных сетях.

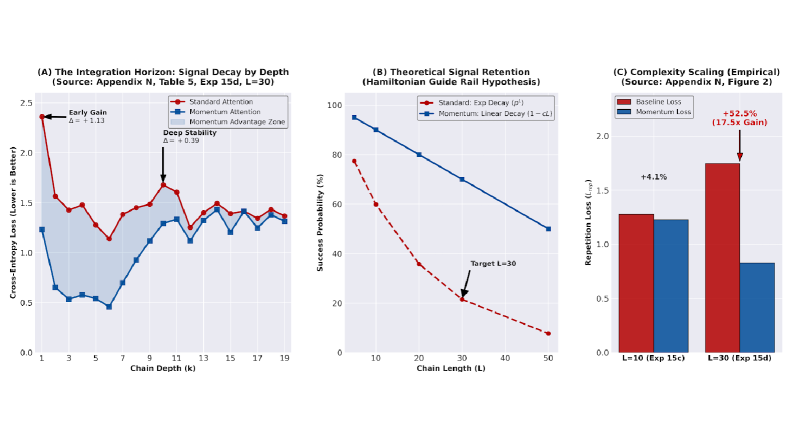
Тестирование на устойчивость к интерференции показывает, что использование механизма накопления импульса обеспечивает экспоненциальное затухание сигнала <span class="katex-eq" data-katex-display="false">p^L</span> по сравнению с линейным затуханием <span class="katex-eq" data-katex-display="false">1-cL</span>, что приводит к увеличению производительности на 52.5% при увеличении длины последовательности с L=10 до L=30 (см. Приложения N, O). — Тестирование на устойчивость к интерференции показывает, что использование механизма накопления импульса обеспечивает экспоненциальное затухание сигнала $p^L$ по сравнению с линейным затуханием $1-cL$ , что приводит к увеличению производительности на 52.5% при увеличении длины последовательности с L=10 до L=30 (см. Приложения N, O).

К Принципиальным Основам Рассуждений Искусственного Интеллекта

Современные разработки в области искусственного интеллекта всё чаще обращаются к фундаментальным принципам физики для создания более эффективных и устойчивых систем. В частности, использование таких понятий, как фазовое пространство и теорема Лиувилля, позволяет по-новому взглянуть на архитектуру ИИ. Эти концепции, изначально разработанные для описания динамики физических систем, предоставляют инструменты для моделирования и анализа поведения сложных сетей, оптимизируя использование ресурсов и повышая устойчивость к шумам и неполным данным. Вместо слепого масштабирования параметров, исследователи стремятся внедрить в ИИ-системы физически обоснованные принципы, что позволяет добиться значительной экономии вычислительных мощностей и повысить общую эффективность. Такой подход не только открывает путь к созданию более компактных и энергоэффективных моделей, но и способствует развитию ИИ, способного к более надежному и предсказуемому рассуждению.

Предложенный подход демонстрирует потенциал преодоления ограничений существующих закономерностей масштабирования в искусственном интеллекте. Вместо простого увеличения вычислительных ресурсов и объёма параметров, исследования направлены на создание систем, способных к более эффективному и человекоподобному рассуждению. В ходе экспериментов модель Momentum, содержащая всего 125 миллионов параметров, достигла сопоставимой производительности с базовой моделью, насчитывающей 350 миллионов параметров, что свидетельствует о повышении эффективности на 64%. Это указывает на возможность создания более компактных и энергоэффективных систем искусственного интеллекта, способных к сложным вычислениям без чрезмерного потребления ресурсов.

Дальнейшие исследования взаимодействия динамических механизмов внимания и индуктивных предубеждений представляются перспективным направлением для создания более мощных и понятных моделей искусственного интеллекта. Особое внимание уделяется тому, как эти механизмы могут быть интегрированы для повышения способности моделей к обобщению и решению сложных задач. Предполагается, что комбинирование динамического внимания, позволяющего модели фокусироваться на наиболее релевантной информации, с индуктивными предубеждениями, закладывающими априорные знания о мире, может значительно улучшить интерпретируемость принимаемых решений. Такой подход позволяет не только повысить эффективность обучения и снизить потребность в огромных объемах данных, но и сделать внутренние процессы модели более прозрачными для анализа и понимания, что является ключевым фактором для построения доверительных и надежных систем искусственного интеллекта.

Представленная работа демонстрирует стремление к математической элегантности в архитектуре нейронных сетей. Введение концепции Momentum Attention, основанной на принципах симплектической механики, не просто улучшает производительность, но и наделяет модель физическими законами сохранения. Это позволяет перейти от эмпирической оценки к доказуемому поведению, что соответствует строгим требованиям к алгоритмической чистоте. Как отмечал Марвин Минский: «Лучшая программа — это та, которую можно доказать корректной». Применение спектральной форензики в анализе Transformer сетей, предложенное авторами, является ярким примером поиска доказуемой логики внутри сложной системы, а не полагаться на статистические тесты.

Что Дальше?

Представленное исследование, хотя и демонстрирует элегантность симплектического подхода к механизмам внимания, оставляет нерешенными фундаментальные вопросы. Простое введение физических законов сохранения не гарантирует понимания, а лишь переносит сложность в другую область. Необходимо строго доказать, что предложенная архитектура действительно обладает свойствами, которые позволяют ей решать задачи индукции в одном слое, а не просто имитирует их. Попытки применить спектральный анализ к фазовому пространству Transformer-сетей представляются перспективными, однако требуют разработки более точных и интерпретируемых метрик.

Очевидным ограничением является предположение о применимости физических аналогий к искусственным нейронным сетям. Попытки найти «физику» в алгоритмах, созданных человеком, могут оказаться бесплодными, если не будут подкреплены строгой математической формализацией. Следующим шагом видится разработка инструментов, позволяющих верифицировать соответствие между физической моделью и реальным поведением сети, а не полагаться на интуитивные соответствия.

В конечном итоге, истинный прогресс в области интерпретируемости машинного обучения потребует не просто новых алгоритмов, а нового взгляда на саму природу интеллекта — искусственного и естественного. Минимизация избыточности, как в коде, так и в концепциях, представляется ключевым принципом, направляющим дальнейшие исследования.

Оригинал статьи: https://arxiv.org/pdf/2602.04902.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-07 22:55