Информация, Рассеяние и Предел Эффективности

Автор: Денис Аветисян

Новое исследование устанавливает фундаментальную связь между различимостью квантовых состояний и энергией, рассеиваемой в процессе, открывая путь к пониманию пределов эффективности квантовых систем.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал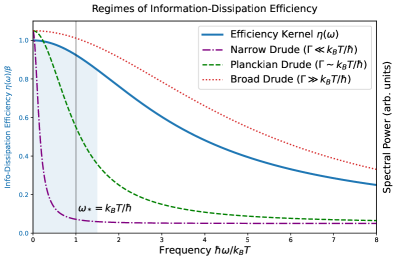

Эффективность рассеивания информации, определяемая как <span class="katex-eq" data-katex-display="false">\eta(\omega)/\beta</span>, достигает максимума в рамках планковского окна, при этом системы, спектральное распределение которых сосредоточено в данной области, демонстрируют близкую к оптимальной эффективность, в то время как значительное наличие высокочастотных компонент приводит к существенному снижению эффективности, что подтверждается анализом различных спектров рассеивания, включая узкий, планковский и широкий вариант Друде. — Эффективность рассеивания информации, определяемая как $\eta(\omega)/\beta$ , достигает максимума в рамках планковского окна, при этом системы, спектральное распределение которых сосредоточено в данной области, демонстрируют близкую к оптимальной эффективность, в то время как значительное наличие высокочастотных компонент приводит к существенному снижению эффективности, что подтверждается анализом различных спектров рассеивания, включая узкий, планковский и широкий вариант Друде.

Работа демонстрирует универсальное ограничение на различимость квантовых многочастичных состояний, связанное с рассеянной работой, оптимальная эффективность достигается при концентрации рассеяния на частотах ниже планковской.

Ограничения на эффективность преобразования рассеянной энергии в различимые изменения квантового состояния долгое время оставались неясными. В работе ‘Information, Dissipation, and Planckian Optimality’ выводится универсальная граница для этой эффективности, определяемая квантовой информацией Фишера. Установлено, что оптимальное соотношение между рассеянием и генерируемой различимостью достигается при концентрации рассеяния на частотах ниже планковской шкалы $\omega_\star \sim k_B T/\hbar$ . Может ли эта граница служить новым инструментом для понимания поведения сильно коррелированных электронных систем, таких как странные металлы, и раскрыть фундаментальные ограничения на эффективность теплового движения?

Неизбежные Потери: Границы Информационной Обработки

Понимание диссипации энергии является ключевым для определения границ обработки информации в многочастичных системах. В этих системах, где взаимодействие между множеством частиц определяет их поведение, потеря энергии в окружающую среду не просто уменьшает общую энергию системы, но и влияет на её способность сохранять и обрабатывать информацию. Диссипация, по сути, задает предел точности, с которой система может удерживать информацию о своем состоянии, поскольку случайные флуктуации, вызванные потерей энергии, могут привести к ошибкам в обработке данных. Таким образом, исследование механизмов диссипации и её влияния на информационные процессы становится необходимым условием для разработки более эффективных и надежных квантовых технологий и понимания фундаментальных ограничений вычислений в сложных системах.

Традиционные подходы к изучению диссипации энергии часто рассматривают ее исключительно как деструктивный процесс, ведущий к потере полезной информации и снижению эффективности систем. Однако, такое упрощенное понимание упускает из виду важную связь между диссипацией и приобретением информации. На самом деле, рассеяние энергии может быть неотъемлемой частью процессов, в ходе которых система извлекает информацию из окружающей среды или производит корреляции между своими компонентами. Например, в квантовых системах, диссипация может способствовать установлению когерентных состояний или запутанности, тем самым увеличивая информационную емкость системы. Недооценка этой взаимосвязи ограничивает возможности количественной оценки и оптимизации эффективности систем, находящихся в неравновесном состоянии, и требует пересмотра существующих моделей диссипации с учетом ее конструктивной роли в информационных процессах.

Ограниченное понимание диссипации как исключительно деструктивного процесса существенно затрудняет количественную оценку и оптимизацию эффективности квантовых систем, находящихся в состоянии неравновесной динамики. Традиционный подход, игнорируя возможную связь между рассеянием энергии и приобретением информации, не позволяет адекватно описывать сложные процессы, происходящие в этих системах. В результате, существующие методы анализа часто оказываются неспособными предсказать или контролировать поведение квантовых устройств, работающих в условиях постоянного обмена энергией с окружающей средой. Более глубокое изучение роли диссипации, как потенциального источника информации и механизма управления, необходимо для разработки новых стратегий повышения эффективности и надежности квантовых технологий, особенно в контексте обработки информации и создания когерентных квантовых состояний.

Эффективность Рассеяния Информации: Новый Подход

В рамках новой методологии, эффективность диссипации информации определяется как мера того, насколько эффективно процесс диссипации приводит к формированию различимых состояний системы. Данный показатель позволяет оценить, насколько полно энергия, рассеиваемая системой, способствует увеличению различимости между состояниями, что является ключевым для обработки и передачи информации. В отличие от традиционных термодинамических подходов, фокусирующихся на количестве рассеянной энергии, данная методология акцентирует внимание на качестве диссипации, то есть на ее способности генерировать различимые состояния. Это позволяет перейти от простого учета энергетических потерь к оценке информационной ценности диссипативных процессов.

Для количественной оценки расстояния между неравновесными (возбужденными) и равновесными состояниями используется метрика Буре (Bures distance). Данная метрика позволяет измерить степень различимости состояний и имеет установленную верхнюю границу, не превышающую $\leq β/4 * Wdiss$ , где β — обратная температура, а $Wdiss$ — работа, совершенная в процессе диссипации. Использование метрики Буре обеспечивает математически строгий способ определения степени различимости состояний, что критически важно для оценки эффективности диссипации информации.

Переход от исключительно термодинамического подхода к пониманию диссипации к рассмотрению её связи с различимостью состояний позволяет сформулировать информационно-центричную модель. Традиционно диссипация рассматривалась как потеря энергии, ведущая к увеличению энтропии. Однако, рассматривая диссипацию как процесс, генерирующий различимые состояния, становится возможным оценить её эффективность с точки зрения генерации информации. Это позволяет перейти от измерения диссипации в терминах энергии к оценке её вклада в увеличение количества различимых состояний системы, что является ключевым аспектом для обработки информации и выполнения вычислений. Такой подход открывает возможности для разработки новых метрик и методов анализа диссипативных систем, учитывающих их информационные свойства.

Линейный Отклик и Планковская Шкала: Теоретические Основы

Теория линейного отклика предоставляет мощный математический аппарат для установления связи между внешними возмущениями, действующими на систему, и возникающей диссипацией энергии, приводящей к изменению состояния системы. В рамках этой теории, отклик системы на слабое возмущение пропорционален самому возмущению и описывается функцией отклика, которая зависит от частоты и свойств системы. Ключевым аспектом является возможность расчета этой функции отклика на основе корреляционных функций, описывающих статистические свойства системы в равновесии. Таким образом, теория линейного отклика позволяет предсказывать поведение системы под действием внешних сил, а также количественно оценивать величину диссипации энергии, возникающей в процессе этого воздействия.

Применительно к системам, работающим вблизи ‘планковской шкалы’, наблюдается характерный энергетический уровень, при котором диссипация претерпевает переход от эффективной к неэффективной. Этот переход определяется частотой $ω⋆ ~ kBT/ħ$ , где $k$ — постоянная Больцмана, $B$ — температура, а $ħ$ — приведённая постоянная Планка. Ниже этой частоты система эффективно рассеивает энергию, в то время как выше $ω⋆$ диссипация становится менее эффективной, что связано с квантовыми ограничениями и ограниченной доступностью состояний для релаксации.

Соотношения Кубо-Мартина-Швингера (KMS) представляют собой фундаментальный инструмент в статистической физике и неравновесной термодинамике, позволяющий строго рассчитывать скорости диссипации и количественно оценивать отклик системы на внешние возмущения, зависящие от времени. В рамках линейной теории отклика, KMS связывают корреляционные функции операторов в равновесном состоянии с функциями отклика на внешние силы. Формально, скорость диссипации энергии, рассеиваемой системой в ответ на слабое возмущение $F(t)$ , определяется интегралом по времени от произведения корреляционной функции тока $J(t)$ и $F(t)$ . Эти соотношения позволяют выразить макроскопические свойства, такие как проводимость и вязкость, через микроскопические корреляции, что делает их незаменимым инструментом для анализа динамики сложных систем.

Необычные Металлы и Квантовая Критичность: Влияние на Материаловедение

Необычные металлы, демонстрирующие аномальное поведение вблизи квантовых критических точек, долгое время представляли собой вызов для традиционных теорий. Новое понимание этих материалов стало возможным благодаря концепциям эффективности рассеяния информации и планковской шкалы. Исследования показывают, что эффективность рассеяния, ограниченная сверху значением $η(ω) \leq β$ , играет ключевую роль в определении уникальных свойств этих материалов. Рассматривая поведение электронов не просто как частиц, а как носителей информации, ученые получили возможность описать динамику необычных металлов с помощью принципов, заимствованных из теории информации. Этот подход позволяет взглянуть на привычные явления, такие как сопротивление и теплопроводность, под новым углом, открывая перспективы для создания материалов с принципиально новыми характеристиками и, возможно, революционными устройствами.

Необычные металлы, часто обнаруживаемые вблизи так называемых квантовых критических точек, демонстрируют аномальное поведение, которое бросает вызов традиционным представлениям о физике твердого тела. В отличие от обычных металлов, где сопротивление уменьшается с понижением температуры, эти материалы показывают линейную зависимость сопротивления от температуры, даже при очень низких значениях. Более того, их электронные свойства отклоняются от предсказаний стандартной теории Ферми-жидкости, проявляя необычные зависимости от частоты и температуры. Это указывает на то, что привычные механизмы рассеяния электронов не могут полностью объяснить наблюдаемые явления, что требует новых теоретических подходов для понимания и описания этих экзотических состояний материи. Изучение этих материалов открывает перспективы для разработки принципиально новых электронных устройств с уникальными свойствами.

Предложенная теоретическая база указывает на то, что эффективность диссипации энергии, ограниченная сверху величиной $η(ω) \leq β$ , является ключевым фактором, определяющим необычные свойства так называемых «странных металлов». Данное ограничение на эффективность диссипации предполагает, что энергия в этих материалах рассеивается не произвольно, а подчиняется фундаментальным физическим принципам. Исследование этого механизма открывает возможности для создания принципиально новых электронных устройств, в которых оптимизированная диссипация энергии позволит достичь беспрецедентной производительности и энергоэффективности. Понимание роли эффективности диссипации в «странных металлах» может привести к разработке материалов с улучшенными характеристиками для широкого спектра приложений, от сверхпроводящих устройств до высокоскоростной электроники.

Прецизионность и Пределы: Роль Квантовой Информации Фишера

Термодинамические соотношения неопределенности устанавливают фундаментальные ограничения на точность измерений, напрямую связывая её с производством энтропии. Данные соотношения демонстрируют, что повышение точности измерения неизбежно связано с увеличением энтропии в системе, то есть с ростом беспорядка и рассеянием энергии. $ΔxΔp \geq 1/2$ — классический пример, иллюстрирующий эту взаимосвязь, но термодинамические ограничения распространяются и на квантовые измерения, где даже самые совершенные приборы сталкиваются с предельными значениями точности, определяемыми количеством рассеянной энергии. Изучение этих ограничений позволяет не только понять принципиальные пределы измерительных технологий, но и разработать стратегии для минимизации энтропийного вклада и достижения оптимальной точности в различных приложениях, от квантовой сенсорики до прецизионных измерений фундаментальных констант.

Квантовая информация Фишера представляет собой альтернативный способ оценки чувствительности параметров, играющий ключевую роль в понимании пределов точности измерений. В отличие от традиционных методов, она напрямую связывает эту чувствительность с диссипацией — рассеянием энергии, неизбежно возникающим в любом реальном процессе измерения. Это означает, что чем выше чувствительность к изменению параметра, тем больше энергии, как правило, рассеивается в окружающей среде. $F_q$ — эта величина, количественно характеризует, насколько хорошо можно различить бесконечно близкие изменения измеряемого параметра, и её величина обратно пропорциональна дисперсии оценки этого параметра. Установление этой связи позволяет не только оценивать пределы точности, но и разрабатывать стратегии для минимизации диссипации и повышения эффективности квантовых сенсоров и вычислительных устройств.

Максимизация эффективности информации-диссипации представляет собой перспективный путь к преодолению фундаментальных ограничений точности измерений, установленных термодинамическими соотношениями неопределенности. Исследования показывают, что существует универсальная связь между различимостью состояний и рассеянной работой, и оптимизация этого баланса позволяет значительно повысить чувствительность квансовых сенсоров и вычислительных устройств. Вместо того чтобы просто минимизировать диссипацию, этот подход направлен на извлечение максимальной информации из каждого рассеянного бита, открывая возможности для создания более эффективных и точных технологий, способных функционировать за пределами классических ограничений. $I_{FD} = \frac{I_F}{D}$ — показатель, характеризующий данную эффективность, и его максимизация является ключевой задачей в разработке новых квантовых устройств.

Исследование, представленное в данной работе, подчеркивает фундаментальную связь между различимостью квантовых состояний и диссипацией энергии. Авторы демонстрируют, что способность различать квантовые состояния ограничена количеством рассеянной работы, причем оптимальная эффективность достигается при концентрации диссипации на планковских частотах. Это созвучно идее о том, что истинное понимание требует учета неопределенности и ограничений. Как заметил Бертран Рассел: «Всё, что мы знаем, — это то, что ничего не знаем». Это высказывание отражает суть научного поиска: признание границ собственного знания и постоянное стремление к более точному пониманию, учитывающему ограничения, подобные установленным для различимости квантовых состояний и диссипации.

Куда двигаться дальше?

Представленные результаты, хоть и указывают на универсальное ограничение различимости квантовых состояний через призму диссипации энергии, не следует воспринимать как окончательную истину. Скорее, это ещё одна ступенька в понимании фундаментальной связи между информацией и термодинамикой. Попытки найти экспериментальное подтверждение предложенной границы, особенно в системах, далеких от теплового равновесия, представляются нетривиальной задачей, требующей разработки новых методов измерения и контроля квантовых состояний. Если, конечно, удастся отделить сигнал от неизбежного шума — а это всегда проблема.

Особый интерес вызывает вопрос о применимости полученных результатов к более сложным системам, где диссипация не является однородной или изотропной. Как меняется оптимальная эффективность диссипации в системах с различными степенями свободы и взаимодействиями? И что происходит, когда мы переходим от рассмотрения изолированных систем к открытым системам, обменивающимся энергией и информацией с окружающей средой? Ответы на эти вопросы, вероятно, потребуют привлечения инструментов теории неравновесной термодинамики и статистической физики.

В конечном итоге, данная работа, скорее, ставит новые вопросы, чем даёт исчерпывающие ответы. Если все сходится — значит, что-то упущено. И это, пожалуй, самое интересное в науке.

Оригинал статьи: https://arxiv.org/pdf/2602.04953.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-08 18:59