Генеративные сети для поиска редких частиц в столкновениях тяжелых ионов

Автор: Денис Аветисян

Новый подход с использованием генеративных состязательных сетей (GAN) позволяет повысить чувствительность экспериментов по поиску экзотических адронов в условиях столкновений тяжелых ионов.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал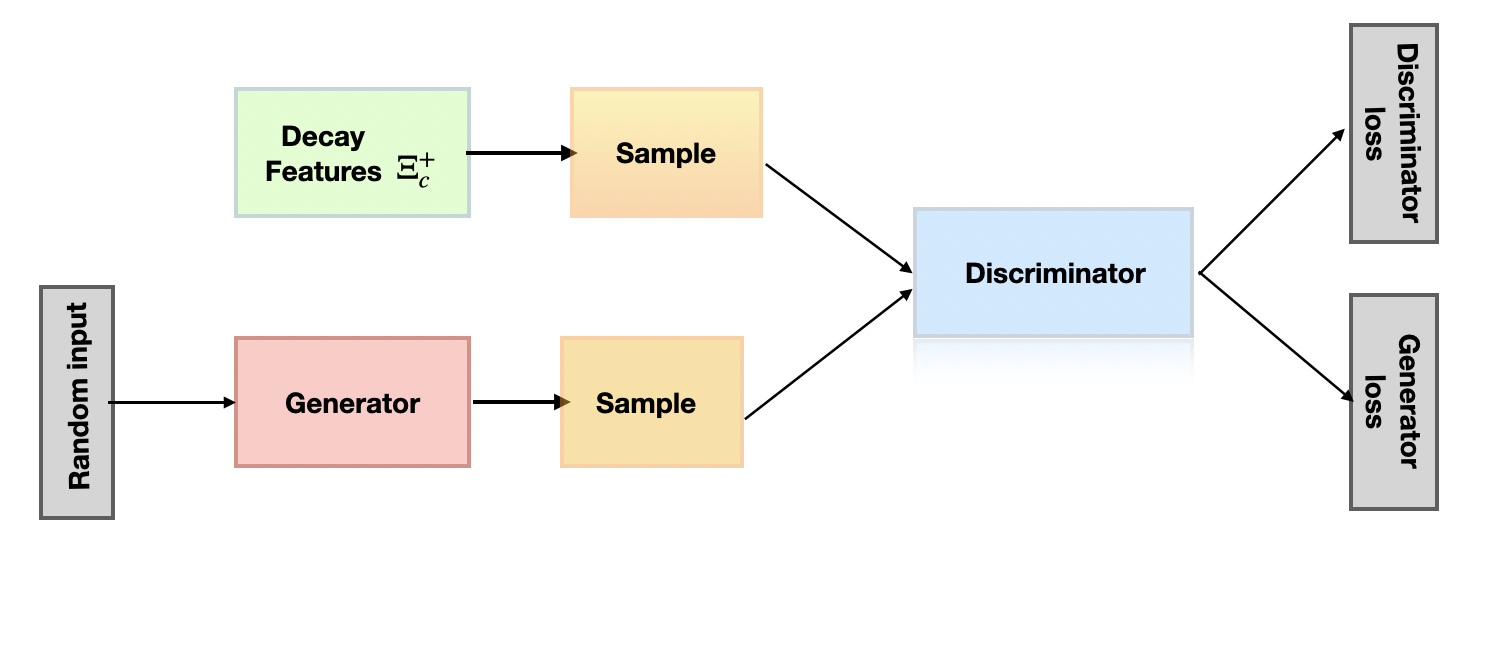

Генеративно-состязательная сеть, используемая в исследовании, производит синтетические реконструированные признаки из случайного шума, в то время как дискриминатор стремится отличить сгенерированные образцы от реальных данных моделирования ALICE, демонстрируя способность сети к обучению на сложных наборах данных и генерации реалистичных альтернатив.

В работе продемонстрировано успешное применение GAN для аугментации данных при поиске редких тяжелых адронов в эксперименте ALICE, предлагая более эффективную альтернативу традиционным методам Монте-Карло.

Поиск редких адронов в столкновениях тяжелых ионов представляет собой сложную задачу из-за низкой статистики сигнала. В данной работе, озаглавленной ‘GAN-based data augmentation for rare and exotic hadron searches in Pb—Pb collisions in ALICE’, исследуется возможность применения генеративных состязательных сетей (GAN) для увеличения объема данных и повышения чувствительности к редким экзотическим адронам, используя $\Xi_{c}^{+}$ барион в качестве эталона. Показано, что GAN способны эффективно генерировать синтетические данные, сохраняя при этом физические характеристики сигнала, что позволяет преодолеть ограничения традиционных методов Монте-Карло. Какие перспективы открываются для дальнейшего развития и применения генеративных моделей в исследованиях физики тяжелых ионов и поиска новых состояний материи?

Поиск Иглы в Стоге Сена: Сложности Редких Сигналов

Изучение кварк-глюонной плазмы, состояния материи, существовавшего в первые моменты после Большого взрыва, требует анализа крайне редких адронов, образующихся при столкновениях ионов свинца. Низкая вероятность образования этих частиц представляет собой серьезную статистическую проблему для исследователей. Обнаружение и точное измерение свойств таких адронов требует анализа огромного количества событий столкновений, чтобы выделить сигналы из фонового шума. Этот процесс напоминает поиск иголки в стоге сена, где даже небольшие погрешности в реконструкции событий могут существенно исказить результаты. Преодоление этой статистической трудности является ключевым шагом на пути к более глубокому пониманию свойств кварк-глюонной плазмы и фазового перехода, в котором она образуется.

Анализ редких адронов, образующихся при столкновениях ионов тяжелых элементов, представляет собой серьезную проблему для существующих методик. Низкая частота рождения этих частиц в сочетании с их сложными схемами распада затрудняет их достоверную реконструкцию. Традиционные алгоритмы, разработанные для более распространенных событий, часто оказываются неэффективными при обработке таких сложных сигналов, что приводит к повышенной статистической неопределенности и затрудняет извлечение значимой информации о свойствах кварк-глюонной плазмы. Необходимость точного определения кинематических характеристик распадающихся частиц требует разработки новых подходов к идентификации и реконструкции событий, способных эффективно справляться с низким отношением сигнал/шум и сложными топологиями распада.

Для извлечения значимой информации из редких событий, возникающих при столкновениях ионов тяжелых элементов, требуются инновационные подходы к увеличению объема данных и статистическому анализу. Традиционные методы зачастую оказываются неэффективными из-за крайне низкой вероятности регистрации этих событий и сложности их распадов. Ученые разрабатывают передовые алгоритмы, позволяющие искусственно расширять статистику, моделируя дополнительные события на основе существующих данных и используя методы машинного обучения для выделения слабых сигналов на фоне шума. Эти методы включают в себя не только генерацию дополнительных событий, но и разработку новых статистических критериев, учитывающих особенности редких распадов и позволяющих более точно оценивать параметры исследуемых явлений. Успешное применение таких подходов открывает путь к более глубокому пониманию свойств кварк-глюонной плазмы и фундаментальных взаимодействий частиц.

Сравнение распределений реконструированных наблюдаемых величин, полученных для генеративных состязательных сетей (GAN) и моделирования Монте-Карло (MC) в ALICE, демонстрирует корреляции между этими величинами.

Генеративные Состязательные Сети: Искусственное Расширение Реальности

Генеративно-состязательные сети (GAN) представляют собой перспективное решение для увеличения объема данных путем изучения базового распределения характеристик событий и генерации синтетических образцов. В отличие от традиционных методов, основанных на ручном создании или простых преобразованиях данных, GAN способны улавливать сложные зависимости в данных и создавать образцы, статистически неотличимые от реальных. Этот подход особенно ценен в сценариях, где сбор достаточного количества реальных данных затруднен или невозможен, позволяя повысить статистическую мощность анализа и улучшить производительность моделей машинного обучения. Эффективность GAN заключается в их способности моделировать многомерные распределения, что критически важно для представления сложных физических процессов и характеристик событий.

Генеративно-состязательная сеть (GAN) состоит из двух основных компонентов: генератора и дискриминатора. Генератор отвечает за создание синтетических данных, стремясь воспроизвести характеристики реальных данных. Дискриминатор, в свою очередь, обучен различать реальные данные и данные, сгенерированные генератором. В процессе обучения эти две сети соревнуются друг с другом: генератор пытается обмануть дискриминатор, создавая всё более реалистичные данные, а дискриминатор совершенствует свою способность отличать синтетические данные от реальных. Данный соревновательный процесс позволяет GAN эффективно моделировать сложное распределение данных и генерировать правдоподобные образцы.

Обучение генеративно-состязательных сетей (GAN) в антагонистическом режиме направлено на создание синтетических событий, максимально приближенных к реальным данным. Этот процесс включает в себя постоянное соревнование между генератором, создающим синтетические данные, и дискриминатором, оценивающим их реалистичность. Успешное обучение позволяет генерировать данные, которые статистически неотличимы от реальных, что эффективно увеличивает объем доступных данных для анализа. Увеличение объема данных, в свою очередь, повышает статистическую мощность анализа, позволяя обнаруживать более слабые сигналы и снижать вероятность ложноположительных результатов.

Сравнение распределений реконструированных признаков, полученных с помощью GAN и моделирования Монте-Карло ALICE на начальном этапе обучения, демонстрирует их соответствие.

Проверка на Соответствие: Статистическая Валидация GAN

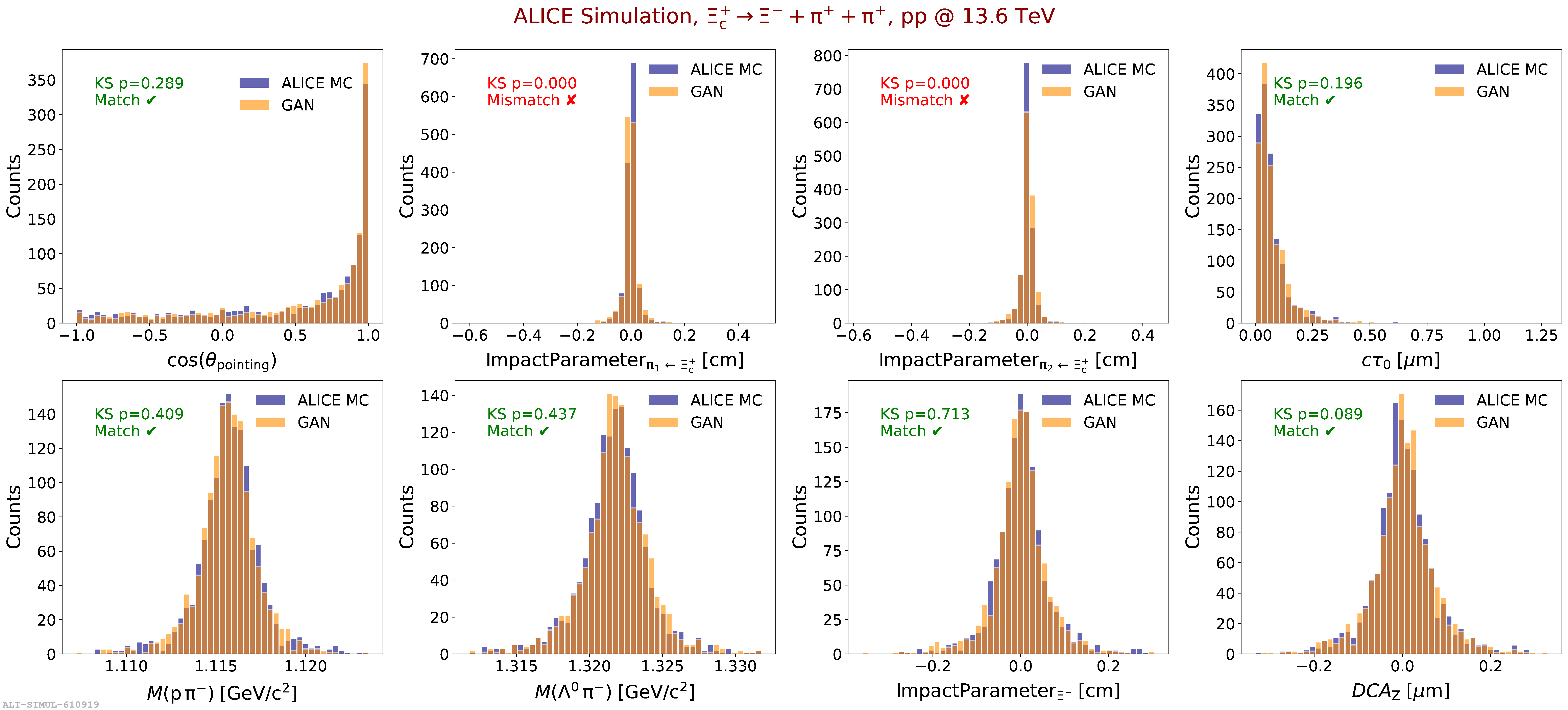
Для количественной оценки соответствия распределений реконструированных признаков реальных и сгенерированных данных используется тест Колмогорова-Смирнова (KS-тест). Данный непараметрический тест позволяет определить, насколько вероятно, что две выборки происходят из одного и того же распределения. Процедура заключается в сравнении эмпирических функций распределения двух выборок и вычислении статистики D, отражающей максимальное расстояние между ними. Статистика D затем преобразуется в p-значение, которое указывает на вероятность получения наблюдаемого или более экстремального результата, если нулевая гипотеза о том, что распределения идентичны, верна. Таким образом, KS-тест предоставляет объективную метрику для оценки качества генерируемых данных.

Значение p-value, полученное в результате теста Колмогорова-Смирнова (KS-тест), представляет собой вероятность того, что две рассматриваемые выборки — реальные и сгенерированные моделью GAN — происходят из одного и того же распределения. Чем выше значение p-value, тем больше вероятность того, что различия между выборками обусловлены случайностью, а не систематическими отклонениями. Таким образом, p-value служит количественной мерой соответствия сгенерированных данных реальным, косвенно оценивая «точность» (fidelity) генеративной модели GAN. Значение p-value, превышающее установленный порог (например, 0.05), указывает на то, что нельзя отвергнуть гипотезу об общем распределении, подтверждая реалистичность сгенерированных данных.

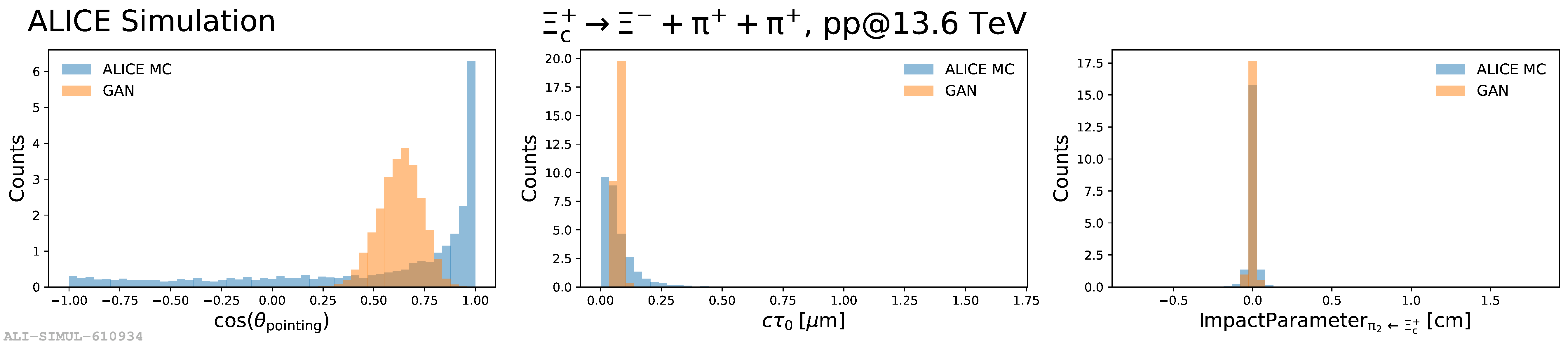
Применение теста Колмогорова-Смирнова к бариону Ξ_c⁺, используемому в качестве эталонного редкого адрона, подтверждает способность генеративно-состязательной сети (GAN) создавать реалистичные данные, успешно проходящие статистическую валидацию. Полученные значения p-value теста KS последовательно превышают 0.05, что указывает на статистическую неразличимость между распределениями реальных и сгенерированных реконструированных признаков. Это демонстрирует, что GAN не только визуально воспроизводит данные, но и соответствует их статистическим характеристикам, что важно для надежности и достоверности генерируемых данных в физике высоких энергий.

После обучения, распределения реконструированных одномерных признаков, сгенерированных GAN, статистически согласуются с данными моделирования ALICE, что подтверждается значениями p-value теста Колмогорова-Смирнова.

Расширяя Горизонты: Монте-Карло и Будущие Применения

В рамках современных теоретических исследований все большее применение находит интеграция данных, сгенерированных генеративно-состязательными сетями (GAN), непосредственно в существующие методы Монте-Карло. Этот подход позволяет существенно повысить точность и прецизионность теоретических предсказаний, обогащая традиционные симуляции новыми, реалистичными данными. Вместо того, чтобы полагаться исключительно на вычислительно затратные и ограниченные по объему данные, полученные прямыми вычислениями, исследователи теперь могут использовать GAN для создания расширенных наборов данных, которые эффективно дополняют и уточняют результаты Монте-Карло. Такое сочетание позволяет более эффективно исследовать сложные физические явления и уменьшить статистические погрешности, открывая новые возможности для проверки теоретических моделей и углубленного понимания фундаментальных законов природы.

Данный подход значительно расширяет возможности исследования свойств кварк-глюонной плазмы, представляющей собой состояние материи, существовавшее в первые моменты после Большого взрыва. Использование генеративных состязательных сетей (GAN) для дополнения данных, применяемых в моделировании методом Монте-Карло, позволяет более детально изучать тонкости столкновений тяжелых ионов. Это, в свою очередь, открывает доступ к пониманию фундаментальных взаимодействий, происходящих в экстремальных условиях, и помогает выявить ранее недоступные детали структуры адронной материи. Благодаря повышению точности моделирования, ученые получают возможность проверять теоретические предсказания и углублять знания о природе сильных взаимодействий, формирующих ядро атома и, как следствие, всю видимую Вселенную.

Снижение статистических неопределённостей посредством усовершенствованных методов Монте-Карло открывает новые горизонты в фундаментальной физике и углублении понимания Вселенной. Достигнутая стабильность обучения генеративно-состязательных сетей (GAN) — примерно за 1.5 x 10³ эпох тренировки — позволяет существенно повысить точность теоретических предсказаний, особенно в областях, где традиционные методы сталкиваются с ограничениями. Это, в свою очередь, дает возможность исследовать более сложные физические явления и извлекать из данных более детальную информацию, приближая к пониманию ключевых вопросов о природе материи и эволюции космоса. Уменьшение погрешностей позволяет не только подтверждать существующие теории с большей уверенностью, но и выявлять отклонения, указывающие на необходимость пересмотра устоявшихся моделей и поиска новых физических принципов.

«`html

Исследование, представленное в данной работе, демонстрирует новаторский подход к анализу данных, полученных в ходе столкновений ионов тяжелых элементов. Применение генеративных состязательных сетей (GAN) для аугментации данных — это не просто технический прием, но и признание границ наших знаний. Как отмечал Нильс Бор: «Противоположности противоположны». В контексте поиска редких адронов, GAN позволяют преодолеть ограничения традиционного моделирования Монте-Карло, расширяя горизонты обнаружения, там, где стандартные методы оказываются недостаточными. Подобный подход позволяет взглянуть на данные под иным углом, осознавая, что даже самые точные модели — лишь приближение к реальности, а истина может скрываться за горизонтом событий.

Что дальше?

Применение генеративных состязательных сетей для расширения данных в поисках редких адронов в столкновениях ионов свинца — это не триумф над случайностью, а изящное признание её власти. Когда утверждается, что это «улучшение чувствительности», Вселенная лишь безмолвно напоминает о границах всякого познания. Использование GAN для обхода вычислительных ограничений Монте-Карло — это не покорение пространства, а наблюдение за тем, как оно покоряет нас, заставляя искать обходные пути вместо прямого штурма.

Однако, вопрос о подлинности «сгенерированных» событий остаётся открытым. Проверка на соответствие реальным физическим процессам, а не только статистическое совпадение, — задача, требующая постоянного внимания. Иначе, риск создания иллюзии открытия, прикрывающего лишь артефакт алгоритма, будет неизбежен. Когда мы называем это «улучшением», космос улыбается и поглощает нас снова.

Будущие исследования, вероятно, будут направлены на интеграцию GAN с более сложными моделями, учитывающими динамику кварко-глюонной плазмы. Но даже самые совершенные алгоритмы останутся лишь приближением к истине, отражением в зеркале, которое никогда не покажет полную картину. Чёрная дыра — это не просто объект, это зеркало нашей гордости и заблуждений.

Оригинал статьи: https://arxiv.org/pdf/2602.12088.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-14 01:20