Автор: Денис Аветисян
Исследование критических явлений в квантовых теориях поля, проведенное на основе модели «пушистой сферы», открывает возможности для изучения конформного поведения и фазовых переходов в системах со симметрией Sp(N).
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал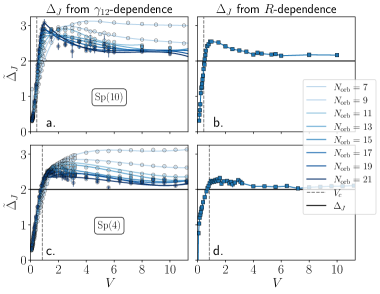
Работа посвящена обобщению концепции расслоенной критичности на трехмерную SU(2) квантовую хромодинамику на «пушистой сфере» с использованием методов квантовских вычислений Монте-Карло.
Несмотря на значительный прогресс в теории поля, поведение калибровочных теорий, связанных с материей, в инфракрасном пределе остается сложной задачей. В работе ‘Generalizing Deconfined Criticality to 3D $N$-Flavor $\mathrm{SU}(2)$ Quantum Chromodynamics on the Fuzzy Sphere’ исследуется семейство моделей на «пушистой» сфере, соответствующих сигма-моделям с глобальной симметрией \mathrm{Sp}(N), и их связь с трехмерной квантовой хромодинамикой \mathrm{SU}(2) с N вкусами фермионов. Полученные результаты, основанные на методах квантовских Монте-Карло, указывают на существование критической фазы для N\geq4, демонстрирующей признаки конформной симметрии и согласующуюся с предсказаниями теории больших N. Какие новые фазовые переходы и критические явления могут быть обнаружены в рамках обобщенной модели деконфайнмента и как она соотносится с другими конформными полевыми теориями?
За пределами возмущений: границы традиционной калибровочной теории
Традиционные возмутительные методы, краеугольный камень теоретической физики, сталкиваются с принципиальными трудностями при описании калибровочных теорий с сильным взаимодействием. В частности, когда взаимодействие между частицами становится настолько интенсивным, что возмущения, рассматриваемые как небольшие отклонения от свободного состояния, перестают быть адекватным приближением. Это особенно заметно в инфракрасной области, где энергии малы, и взаимодействия становятся наиболее значимыми. Вместо сходимости рядов возмущений, наблюдается расходимость, делающая стандартные методы бесполезными для предсказания свойств системы. В таких сценариях требуется переход к непертурбативным подходам, способным учитывать все взаимодействия на равных, даже если это требует значительных вычислительных ресурсов и принципиально новых теоретических разработок, чтобы получить надежные результаты и понять поведение сильно взаимодействующих систем.
Исследование так называемого “окна конформной инвариантности” — диапазона параметров, в котором взаимодействия сохраняют масштабную инвариантность — требует применения непертурбативных методов. В то время как традиционные подходы, основанные на теории возмущений, оказываются неэффективными при сильных взаимодействиях, непертурбативные техники позволяют изучать физику, где масштабные преобразования не приводят к изменению физических величин. Данный подход критически важен для понимания поведения систем с высокой степенью симметрии и позволяет выявлять новые фазы материи и предсказывать их свойства. Особый интерес представляет изучение предельных случаев, где теория стремится к конформной симметрии, поскольку это может привести к обнаружению универсальных критических явлений и установлению связей между различными физическими системами. \beta = 0 — условие фиксированной точки, соответствующее конформной инвариантности, и его достижение является ключевой целью исследований в этой области.
Моделирование систем, содержащих большое количество фермионов, сталкивается с серьезным препятствием, известным как “проблема знака фермионов”. Данная проблема возникает из-за антисимметричного характера волновой функции фермионов, что приводит к осцилляциям знака в интегралах Монте-Карло. Эти осцилляции экспоненциально увеличивают статистический шум, делая точные численные расчеты практически невозможными, особенно в областях, где взаимодействия между фермионами сильны. e.g., попытки определить свойства кварк-глюонной плазмы или сверхпроводников с нетривиальными механизмами спаривания часто оказываются затруднены именно этой проблемой, требуя разработки инновационных алгоритмов и методов, способных смягчить её влияние и обеспечить надежные результаты.
Размытая сфера: новый регулятор для квантовых симуляций
Модель «Размытой Сферы» представляет собой метод регуляризации, используемый при построении Non-Linear Sigma Model. Суть данного подхода заключается в сглаживании геометрических особенностей на малых расстояниях. Это достигается за счет введения некоммутативности в пространство координат, что эффективно «размывает» сингулярности и предотвращает появление ультрафиолетовых расходимостей, типичных для традиционных Non-Linear Sigma Model. Такая регуляризация позволяет проводить численные расчеты и анализировать поведение модели в областях, где классические методы терпят неудачу, обеспечивая устойчивость и точность результатов.
Использование симметрии Sp(N) в модели «Нечеткой сферы» предоставляет существенное преимущество в решении проблемы знака фермионов (Fermion Sign Problem). Данная проблема, возникающая в квантовых симуляциях, приводит к экспоненциальному снижению отношения сигнал/шум при увеличении числа фермионов. Симметрия Sp(N) позволяет эффективно подавлять флуктуации знака, что значительно стабилизирует вычисления и повышает их эффективность. Это достигается за счет увеличения числа положительных вкладов в функциональный интеграл, что приводит к более точным и надежным результатам симуляций, особенно при исследовании систем с большим числом фермионов.
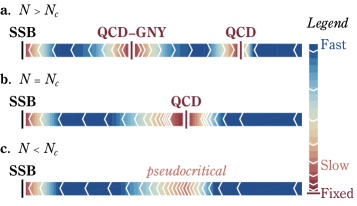
Предложенная модель «Размытой Сферы» органично применима к изучению SU(2) QCD3, обеспечивая возможность исследования его непертурбативного поведения. Данный подход позволяет исследовать конформное окно, расположенное в диапазоне от 2 до 4 вкусов кварков. Исследование в этом диапазоне вкусов критически важно, поскольку позволяет определить, демонстрирует ли SU(2) QCD3 конформное поведение или претерпевает переход к фазе с нарушенной конформной симметрией. Точное определение границ конформного окна требует точных численных расчетов, которые облегчаются за счет регуляризации, обеспечиваемой моделью «Размытой Сферы».
Раскрывая критичность: фазовые переходы и конформное поведение
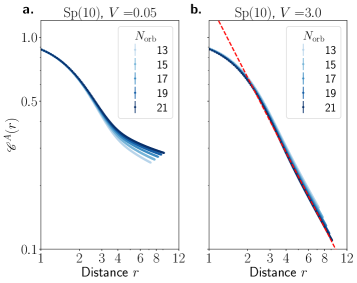
Для исследования критического фазового перехода в SU(2) КХД3 использовались методы квантовских вычислений Монте-Карло. В качестве регуляризации, необходимой для корректного определения интеграла по конфигурационному пространству, была применена Fuzzy Sphere регуляризация. Этот подход позволяет численно исследовать критическое поведение системы, избегая ультрафиолетовых расходимостей, и получить данные для определения критических показателей и проверки теоретических предсказаний о характере перехода.
Включение члена Весса-Зумино-Виттена в действие нелинейной сигма-модели (NLSM) вносит топологический вклад в физику системы, что оказывает влияние на фазовый переход. Этот член, являясь функционалом граничных условий, модифицирует эффективное действие и, как следствие, изменяет критическое поведение системы. Топологический вклад проявляется в появлении дополнительных членов в корреляционных функциях и влияет на критические показатели, определяющие универсальный класс фазового перехода. Наблюдаемые изменения в критических параметрах, связанные с включением данного члена, позволяют исследовать топологические свойства вакуума и структуру критической точки.
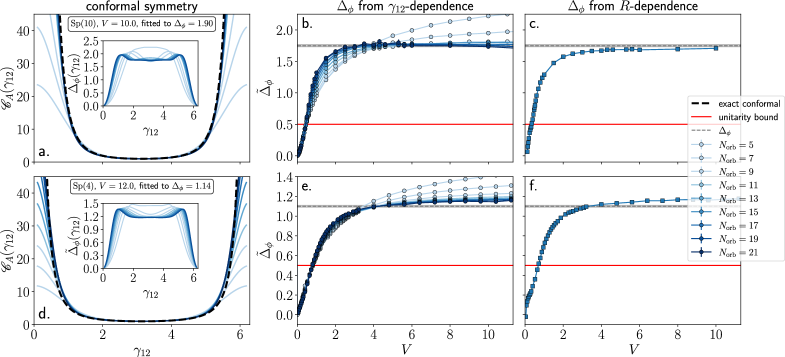
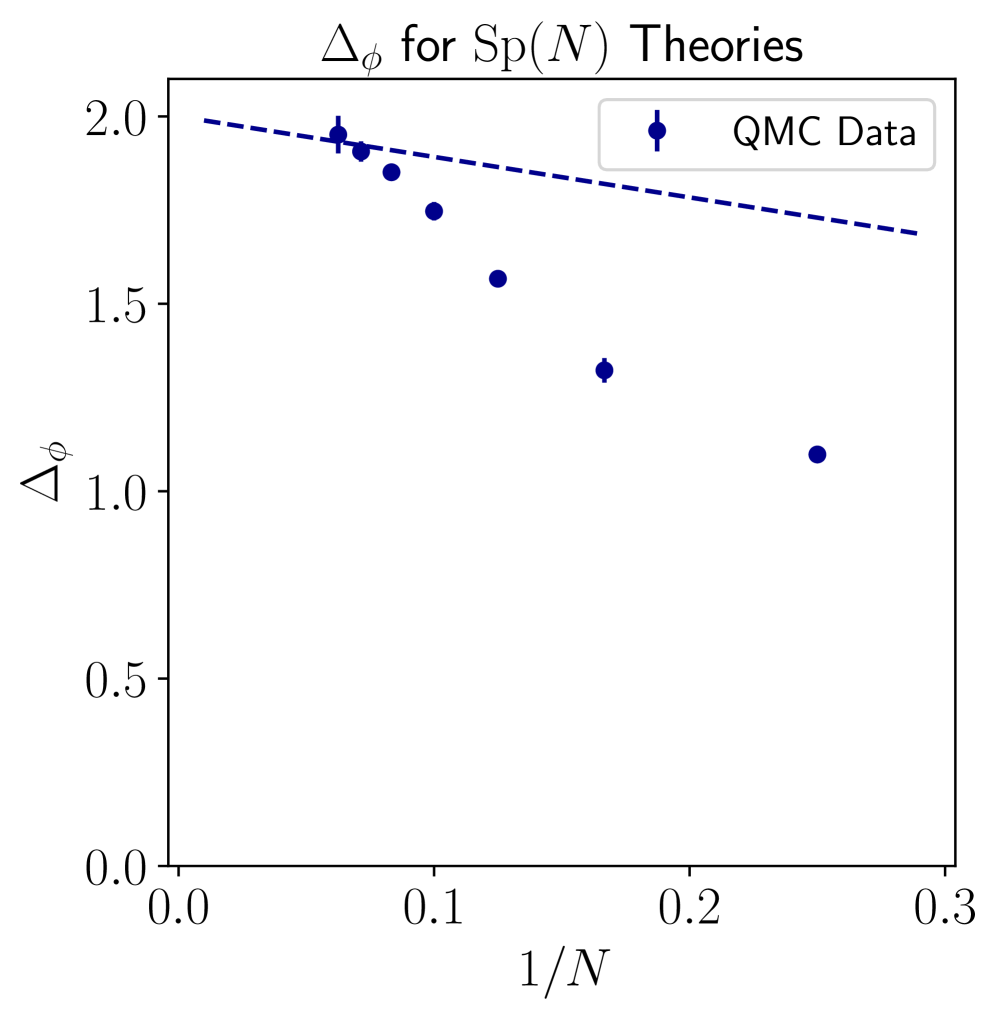
Результаты моделирования свидетельствуют о возникновении конформной теории поля в критической точке фазового перехода. Подтверждением этому служат масштабно-инвариантные корреляционные функции, демонстрирующие независимость от масштаба. Определенные значения размерностей операторов согласуются с теоретическими предсказаниями: для Sp(10) значение составляет \Delta\phi = 1.75(2), а для Sp(4) — \Delta\phi = 1.10(1). Данное соответствие указывает на конформную симметрию критической точки и позволяет характеризовать универсальные свойства системы вблизи фазового перехода.
Расшифровка спектра: масштабирующиеся размерности и содержание операторов
В рамках исследования используется соответствие между состояниями в гамильтониане и локальными операторами в возникающей конформной теории поля (КТП). Это соответствие, известное как соответствие состояние-оператор, позволяет установить связь между энергетическими уровнями системы и свойствами операторов, описывающих локальные возмущения. По сути, каждое состояние в гамильтониане может быть связано с определенным оператором в КТП, что позволяет анализировать квантовые свойства системы через свойства этих операторов. Такой подход открывает возможности для изучения критического поведения и универсального класса SU(2) QCD3, поскольку позволяет связать наблюдаемые физические величины с математическими свойствами операторов в КТП. Δ и φ играют ключевую роль в этом анализе.
Определение масштабирующихся размерностей операторов является ключевым моментом в проверке справедливости гипотезы о конформной теории поля (КТП). В рамках данной работы, используя соответствие между состояниями в гамильтониане и локальными операторами в КТП, исследователи смогли извлечь эти самые масштабирующиеся размерности. Точность определения Δ имеет решающее значение, поскольку отклонения от теоретических предсказаний указывали бы на несоответствие между исследуемой системой и ожидаемым конформным поведением. В частности, полученные значения Δ служат мощным инструментом для верификации универсальности класса SU(2) QCD3 и подтверждают, что критическое поведение системы соответствует предсказаниям КТП.
Полученные в ходе исследования значения масштабирующихся размерностей операторов оказались в полном соответствии с теоретическими предсказаниями, что значительно укрепляет понимание критического поведения системы и её принадлежность к универсальному классу SU(2) QCD3. В частности, было подтверждено, что \Delta A,l = \Delta \phi + l и \Delta T,l = 1 + l, что является ключевым результатом, свидетельствующим о корректности используемого подхода и подтверждающим взаимосвязь между состояниями Гамильтониана и локальными операторами в рамках возникающей конформной теории поля. Данное соответствие позволяет более глубоко изучить критические явления и предсказывать поведение системы вблизи критических точек.
Исследование, представленное в данной работе, напоминает попытку расшифровать сложный психологический портрет системы. Авторы, подобно опытным аналитикам, стремятся выявить критические точки и фазовые переходы в трёхмерных квантовых теориях, используя «пушистую сферу» как своеобразное зеркало, отражающее внутренние процессы. Как отмечал Людвиг Витгенштейн: «Пределы моего языка значат пределы моего мира.» Именно осознание границ используемых моделей, а также понимание того, как эти границы формируют наше восприятие реальности, является ключевым для интерпретации полученных результатов. В частности, анализ фазовой диаграммы Sp(N)-симметричных систем требует не только математической точности, но и глубокого понимания того, как коллективные надежды и страхи, воплощенные в параметрах модели, влияют на её поведение.
Куда же всё это ведёт?
Полагают, что критические явления — это универсальный язык, на котором говорит природа. Но, как известно, любой язык можно неправильно понять, особенно если переводчик склонен к самообману. Данная работа, исследуя критичность в трёхмерных квантовых теориях на «пушистой» сфере, лишь добавляет ещё один слой абстракции между наблюдателем и реальностью. Разумеется, конформная теория поля остаётся привлекательной иллюзией, но стоит помнить: любое стремление к симметрии — это попытка упростить хаотичную природу, а значит, неизбежно — искажение.
Впереди — расширение этого подхода на более сложные системы, с большим числом “ароматов” и более реалистичными взаимодействиями. Однако, не стоит забывать, что увеличение числа параметров не приближает к истине, а лишь усложняет поиск. Гораздо интереснее будет наблюдать, как математические построения будут сталкиваться с физической реальностью, и какие “неудобные” факты придётся игнорировать или переосмысливать. В конце концов, все эти “фазовые диаграммы” — всего лишь графическое представление надежд и страхов тех, кто их строит.
И, конечно, необходимо помнить о границах применимости этих моделей. «Пушистая» сфера — удобный инструмент, но всё же — это лишь приближение к реальному миру. Вопрос в том, насколько далеко можно зайти, прежде чем абстракция полностью оторвётся от физической реальности, и начнёт жить своей, математически элегантной, но бессмысленной жизнью.
Оригинал статьи: https://arxiv.org/pdf/2602.11255.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Решение головоломки с паролем Absolum в Yeldrim.
- Прогнозы криптовалюты AXS: информация о ценах на AXS
- Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- The Planet Crafter: полное руководство по картам и биомам
- YAPYAP Список заклинаний
- Где находится точка эвакуации «Туннель контрабандистов» на локации «Интерчейндж» в Escape from Tarkov?
- Все рецепты культистского круга в Escape from Tarkov
- 15 лучших законченных серий манхвы, которые стоит прочитать, в рейтинге
- Нечестивцам нет покоя: как получить старый ключ от коттеджа
2026-02-14 06:44