Гравитация за пределами Эйнштейна: Точные вычисления отклонений

Автор: Денис Аветисян

Новое исследование представляет собой детальную оценку пост-ньютоновских параметров в скалярно-тензорных теориях гравитации, раскрывая потенциальные различия с общей теорией относительности в экстремальных условиях.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал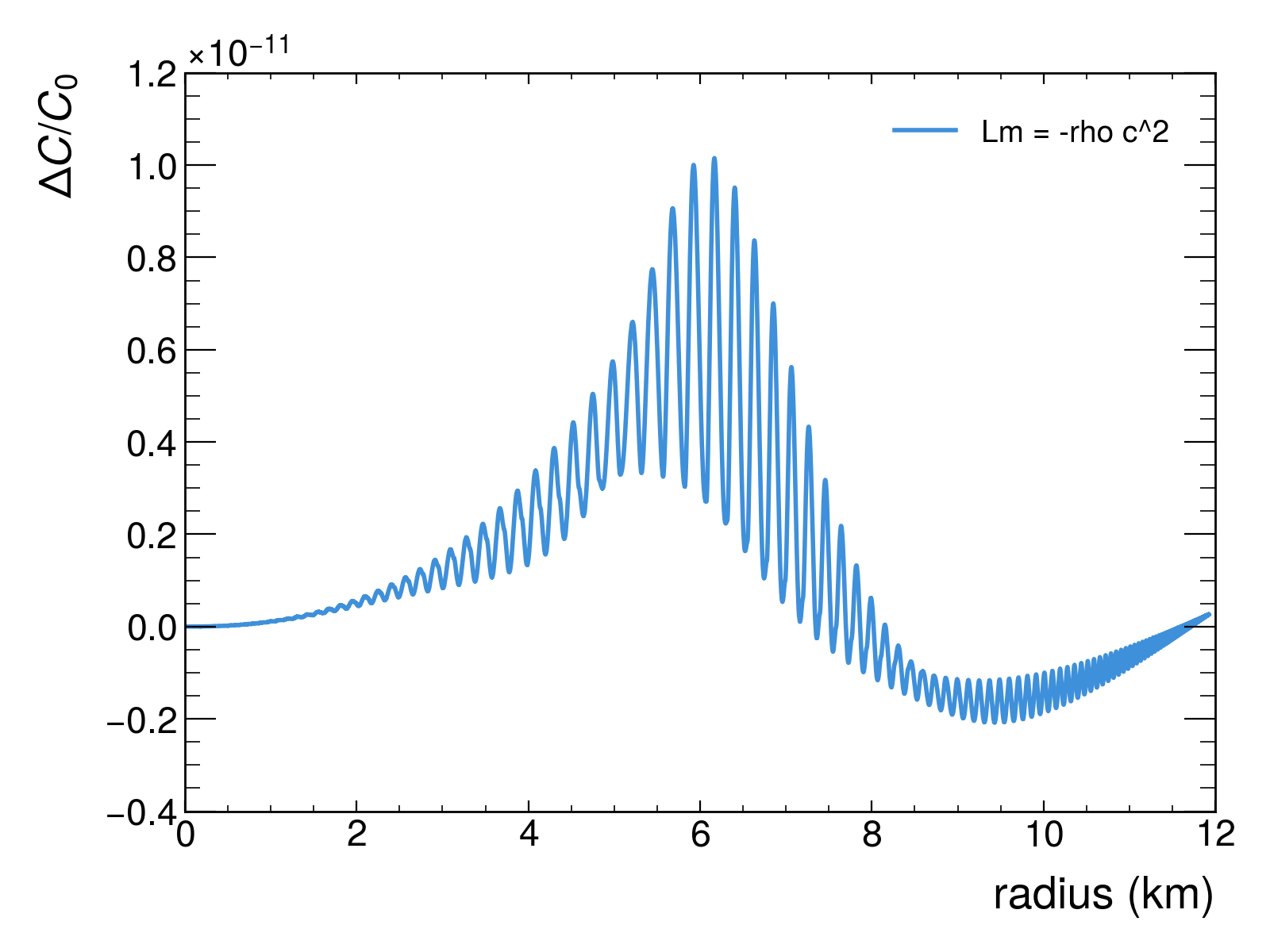

Наблюдается изменение относительной величины константы <span class="katex-eq" data-katex-display="false">\frac{C\_{i}-C\_{0}}{C\_{0}}</span> в процессе численного интегрирования, зависящее от радиуса в рамках теории «запутанной относительности» при центральной плотности в 100 МэВ/фм³, что демонстрирует взаимосвязь между геометрией и константами в данной модели. — Наблюдается изменение относительной величины константы $\frac{C\_{i}-C\_{0}}{C\_{0}}$ в процессе численного интегрирования, зависящее от радиуса в рамках теории «запутанной относительности» при центральной плотности в 100 МэВ/фм³, что демонстрирует взаимосвязь между геометрией и константами в данной модели.

Численное вычисление точных пост-ньютоновских параметров в теориях Бранса-Дике и «запутанной» относительности позволяет оценить отклонения от предсказаний общей теории относительности и ограничить параметры моделей по наблюдениям дипольного гравитационного излучения.

Традиционные пост-ньютоновские параметры, используемые в теориях гравитации, могут оказаться недостаточными при рассмотрении сильно гравитирующих объектов. В работе ‘On the numerical evaluation of the `exact’ Post-Newtonian parameters in Brans-Dicke and Entangled Relativity theories’ разработаны новые методы численного вычисления так называемых «точных» параметров в скалярно-тензорных теориях гравитации, таких как Brans-Dicke и Entangled Relativity. Полученные результаты демонстрируют, что различие между точными и стандартными параметрами может достигать 80% в некоторых случаях, что указывает на потенциальную возможность обнаружения отклонений от общей теории относительности посредством наблюдений, например, дипольного гравитационного излучения. Каким образом будущие эксперименты смогут ограничить параметры этих теорий и пролить свет на природу гравитации?

За пределами ньютоновской гравитации: Поиск более глубокого понимания

Несмотря на свою удивительную точность в широком диапазоне условий, ньютоновская теория гравитации оказывается несостоятельной в областях с экстремально сильными гравитационными полями. Это требует применения релятивистских поправок, учитывающих эффекты, пренебрежимо малые при слабых полях, но приобретающие решающее значение вблизи сверхплотных объектов, таких как нейтронные звезды или черные дыры. Традиционное описание гравитации, основанное на ньютоновском приближении, перестает давать адекватное описание динамики в таких средах, поскольку не учитывает искривление пространства-времени и связанные с ним нелинейные эффекты. Таким образом, для понимания физики экстремальных гравитационных систем необходимо переходить к общей теории относительности Эйнштейна, которая обеспечивает более полное и точное описание гравитации в любых условиях.

Стандартный подход к описанию отклонений от ньютоновской гравитации опирается на использование так называемых пост-ньютоновских параметров. Эти параметры представляют собой набор величин, позволяющих количественно оценить поправки к ньютоновскому закону всемирного тяготения в слабых гравитационных полях. Суть метода заключается в построении последовательного разложения, или пертурбативного расширения, где отклонения от ньютоновского закона рассматриваются как малые поправки. В рамках этого подхода, гравитационное поле описывается как сумма ньютоновского компонента и небольших поправок, зависящих от пост-ньютоновских параметров. Изучение этих параметров позволяет проверить общую теорию относительности в слабом поле и оценить границы применимости ньютоновской гравитации.

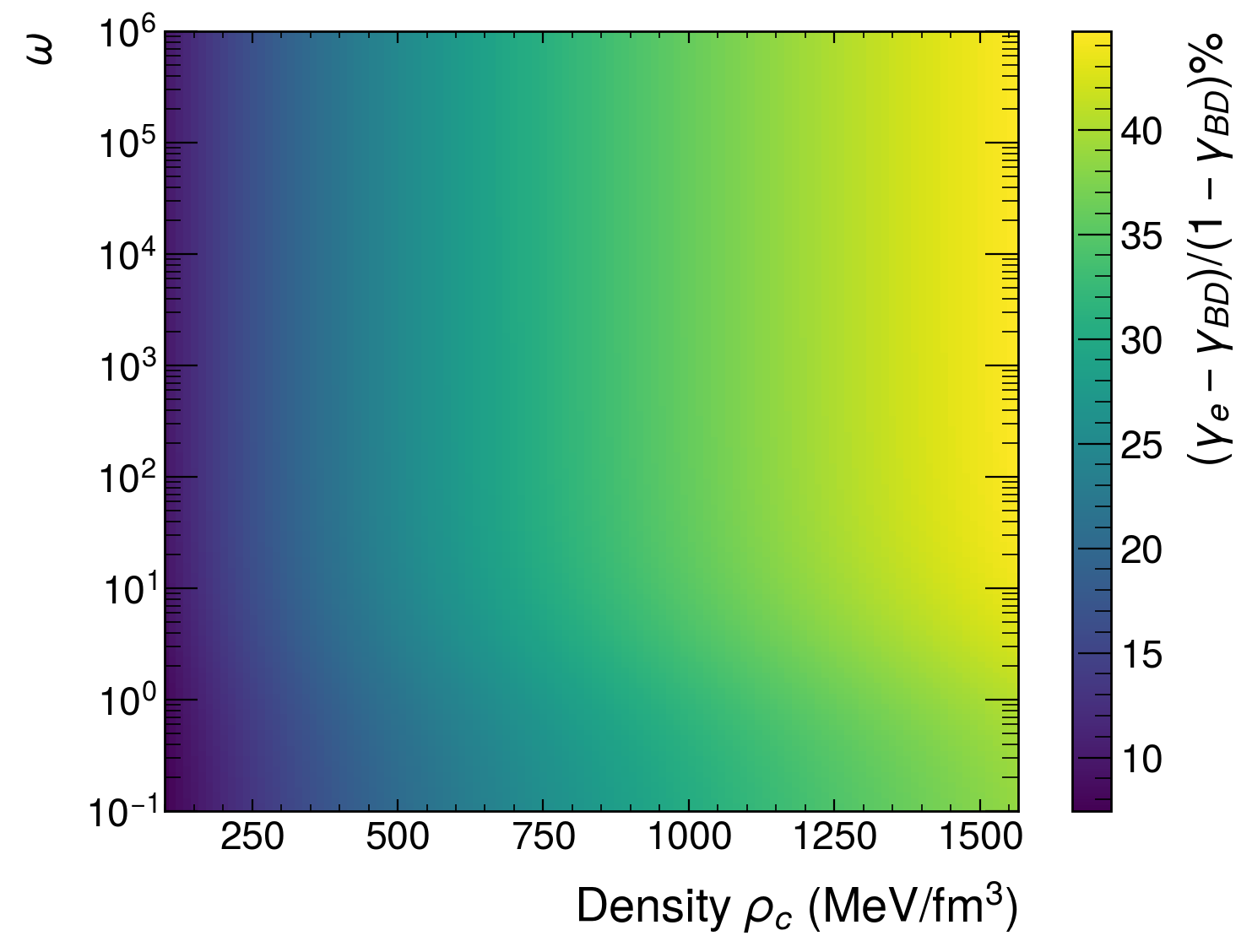
Постньютоновские параметры, широко используемые для описания отклонений от ньютоновской гравитации, имеют существенные ограничения, связанные с допущениями о слабом поле и медленных движениях. Исследования показали, что для нейтронных звезд отклонение точного пост-ньютоновского параметра γ от единицы может достигать 16.1%. Данный результат демонстрирует значительное влияние сильных гравитационных полей, которые не могут быть адекватно учтены стандартными приближениями, и подчеркивает необходимость разработки более точных методов для изучения гравитации в экстремальных астрофизических условиях. Это особенно важно для понимания поведения нейтронных звезд и черных дыр, где гравитация является доминирующей силой.

Сравнительный анализ параметров γ в точных и стандартных пост-ньютоновских расчетах для 150 комбинаций значений ω (от <span class="katex-eq" data-katex-display="false">10^{-1}</span> до <span class="katex-eq" data-katex-display="false">10^{6}</span>) и центральной плотности (от 100 до 1570 МэВ/фм³), ограниченных условием скорости звука в нейтронной звезде, не превышающей <span class="katex-eq" data-katex-display="false">c/\sqrt{3}</span>, показывает относительное отклонение между определениями γ, представленное цветовой шкалой в процентах. — Сравнительный анализ параметров γ в точных и стандартных пост-ньютоновских расчетах для 150 комбинаций значений ω (от $10^{-1}$ до $10^{6}$ ) и центральной плотности (от 100 до 1570 МэВ/фм³), ограниченных условием скорости звука в нейтронной звезде, не превышающей $c/\sqrt{3}$ , показывает относительное отклонение между определениями γ, представленное цветовой шкалой в процентах.

Спутанная относительность: Новый взгляд на природу гравитации

В рамках теории “Переплетенная Относительность” (Entangled Relativity) предлагается более фундаментальное описание гравитации, в котором связь между материей и геометрией пространства-времени является нелинейной. В отличие от общей теории относительности, где гравитация описывается как следствие искривления пространства-времени под воздействием массы-энергии в рамках линейного приближения, данная теория постулирует, что взаимодействие материи и геометрии происходит посредством нелинейных членов в соответствующих уравнениях. Это означает, что влияние материи на геометрию не является просто пропорциональным её плотности энергии, а включает в себя более сложные взаимодействия, которые могут приводить к отклонениям от предсказаний общей теории относительности, особенно в экстремальных гравитационных условиях. Нелинейность связи может проявляться в виде дополнительных членов в уравнениях Эйнштейна, описывающих гравитационное поле, и требует использования более сложных математических методов для получения решений.

В рамках теории «Спутанной Относительности» гравитационное взаимодействие моделируется посредством скалярного поля $\phi(x)$ , что является отходом от тензорного подхода общей теории относительности. В отличие от гравитона, частицы-переносчики взаимодействия в общей теории относительности, скалярное поле представляет собой единое поле, влияющее на метрику пространства-времени. Это приводит к модифицированным уравнениям поля, отличным от уравнений Эйнштейна, и предсказывает отклонения от ньютоновской гравитации на различных масштабах. В частности, использование скалярного поля позволяет описывать эффекты, не наблюдаемые в рамках общей теории относительности, такие как изменение гравитационной постоянной во времени и пространстве, а также появление дополнительных степеней свободы, влияющих на динамику черных дыр и космологических моделей.

Для построения решений в рамках теории «Спутанная Относительность» и моделирования внешнего пространства-времени часто используются сложные математические методы, в частности, метрика Яниса-Ньюмена-Виникура (Janis-Newman-Winicour metric). Эта метрика представляет собой параметризованное решение уравнений Эйнштейна, позволяющее аналитически описывать геометрию вокруг стационарных, осесимметричных источников массы и энергии. Использование данной метрики существенно упрощает задачу поиска решений для конкретных физических сценариев, таких как вращающиеся черные дыры или звездные системы, и позволяет исследовать отклонения от предсказаний общей теории относительности, возникающие в рамках «Спутанной Относительности». Ключевым преимуществом является возможность введения произвольных параметров, определяющих характер гравитационного поля, что обеспечивает гибкость при моделировании различных астрофизических объектов и явлений. $g_{\mu\nu}$ — тензор метрики, описывающий геометрию пространства-времени.

Моделирование компактных звезд: Уравнения Толмана-Оппенгеймера-Волкова

Уравнения Толмана-Оппенгеймера-Волкова (TOV) представляют собой систему дифференциальных уравнений, описывающих структуру и стабильность релятивистских звезд. Эти уравнения являются обобщением уравнений гидростатического равновесия для случая общей теории относительности, учитывая гравитационное воздействие массы звезды на ее внутреннее давление и плотность. Решение уравнений TOV требует знания уравнения состояния (EOS) вещества, составляющего звезду, и позволяет определить зависимость массы звезды от ее радиуса. Ключевыми переменными в этих уравнениях являются метрика пространства-времени, описывающая геометрию вокруг звезды, и давление как функция радиуса. $\frac{dP}{dr} = - \frac{G m(r) \rho(r)}{r^2} \left( 1 + \frac{P(r)}{\rho(r)} \right) \left( 1 + \frac{2 G P(r)}{\rho(r) c^2} \right)$ — основное уравнение, определяющее градиент давления как функцию радиуса, массы и плотности.

Применение уравнений Толмана-Оппенгеймера-Волкова в рамках теории «Запутанной Относительности» позволяет исследовать влияние скалярного поля на максимальную массу и радиус нейтронных звезд. В рамках данной теории, скалярное поле взаимодействует с материей звезды, изменяя ее уравнение состояния и, следовательно, ее гидростатическое равновесие. Результаты показывают, что наличие скалярного поля может как увеличивать, так и уменьшать максимальную массу нейтронной звезды по сравнению со стандартной моделью, в зависимости от силы взаимодействия и параметров поля. Изменение радиуса также наблюдается, при этом более сильное взаимодействие обычно приводит к уменьшению радиуса при заданной массе. Эти изменения критически важны для понимания эволюции и конечной судьбы массивных звезд, а также для интерпретации астрофизических наблюдений, таких как гравитационные волны от слияния нейтронных звезд.

Полученные решения позволяют вычислить точные пост-ньютоновские параметры, сохраняющие свою валидность даже в сильном гравитационном поле. Анализ показывает, что отклонение параметра δ_exact от единицы для нейтронных звезд может достигать 40.1%. Данный факт подчеркивает значимость поправок, учитывающих сильные поля гравитации, и необходимость использования точных решений для адекватного моделирования структуры и эволюции компактных звезд, в особенности при высоких плотностях и давлениях, где стандартные ньютоновские приближения становятся неприменимы.

Зависимость скорости изменения импульса <span class="katex-eq" data-katex-display="false">\dot{P}^{D}</span> от предсказанной массы нейтронной звезды демонстрирует различия в зависимости от используемого уравнения состояния. — Зависимость скорости изменения импульса $\dot{P}^{D}$ от предсказанной массы нейтронной звезды демонстрирует различия в зависимости от используемого уравнения состояния.

Гравитационные волны и поиск новой физики

Дипольные гравитационные волны, возникающие из-за асимметричного распределения массы, представляют собой уникальный инструмент для проверки теорий модифицированной гравитации. В отличие от предсказаний общей теории относительности, многие альтернативные модели допускают существование таких волн, даже в системах, где массы распределены неравномерно. Изучение характеристик этих волн, таких как их амплитуда и поляризация, позволяет получить информацию о фундаментальных свойствах гравитационного взаимодействия и выявить отклонения от стандартной модели. Обнаружение дипольного излучения стало бы явным указанием на необходимость пересмотра существующих гравитационных теорий и могло бы открыть новые горизонты в понимании природы гравитации и структуры Вселенной. Анализ этих волн позволяет тестировать различные сценарии, предполагающие наличие дополнительных измерений или модификаций уравнения Эйнштейна, предлагая перспективный путь к обнаружению «новой физики» за пределами известных границ.

Интенсивность дипольного гравитационного излучения, возникающего при асимметричном распределении массы, количественно оценивается с помощью параметра Дамура-Эспозито-Фарезе. Этот параметр, по сути, служит мерой отклонения от предсказаний общей теории относительности и позволяет оценить степень нарушения локальной лоренц-инвариантности. Наблюдения гравитационных волн, в особенности, анализ формы сигнала и амплитуды, позволяют накладывать ограничения на значение этого параметра. Чем точнее измерены характеристики гравитационных волн, тем более строгими становятся ограничения на параметр Дамура-Эспозито-Фарезе, что, в свою очередь, позволяет проверять различные модификации теории гравитации и искать признаки новой физики за пределами стандартной модели. Фактически, этот параметр выступает в роли чувствительного индикатора, позволяющего оценить вероятность существования альтернативных теорий гравитации и выявить потенциальные отклонения от предсказаний Эйнштейна.

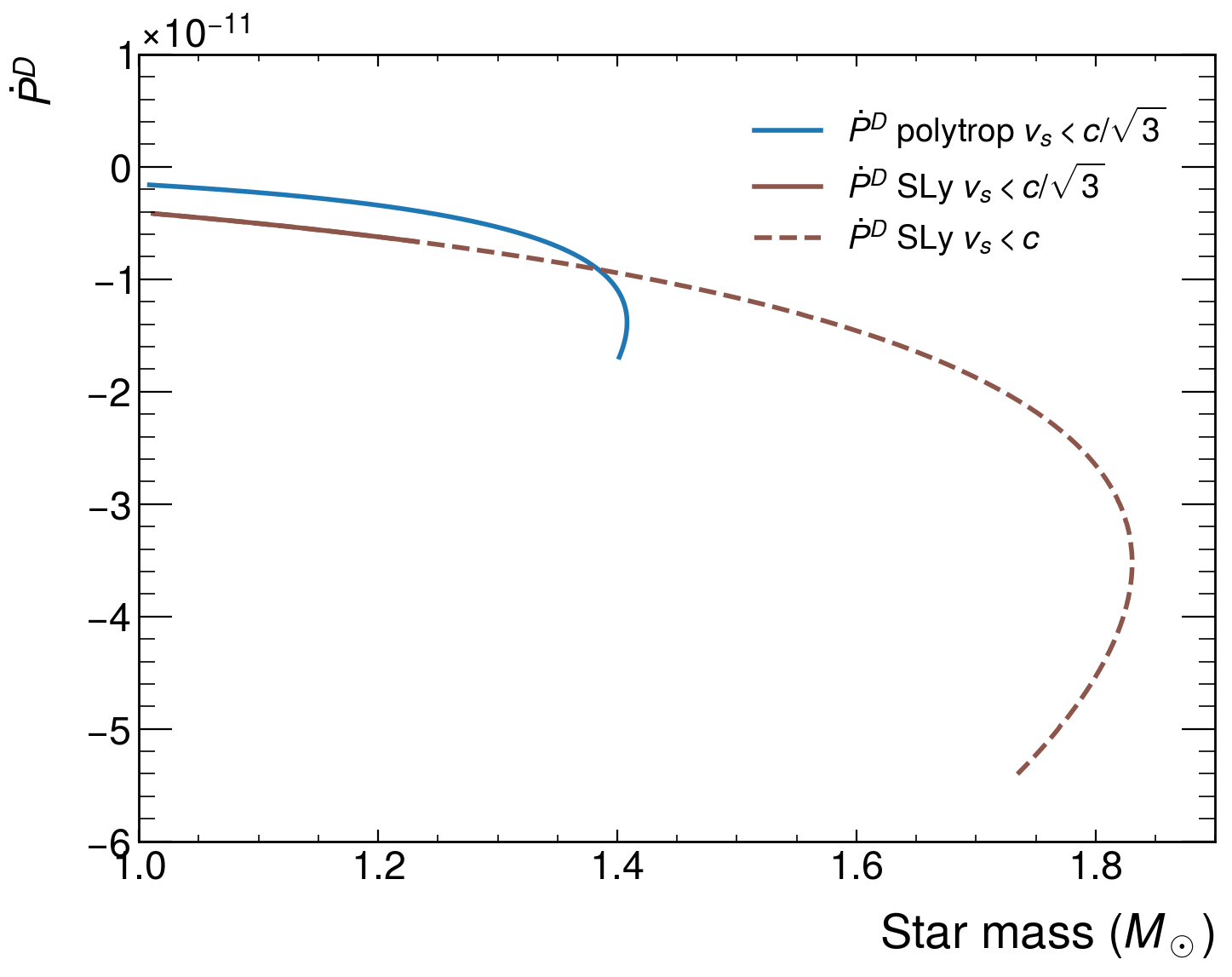
Сравнение предсказанных и наблюдаемых форм гравитационных волн представляет собой мощный инструмент для проверки справедливости теории «спутанной относительности» и других альтернативных теорий гравитации, потенциально открывая новую физику, выходящую за рамки общей теории относительности. Проведенные расчеты указывают на диапазон изменения орбитального периода ( $Pdot$ ) от -1.69 x 10^-11 до -1.62 x 10^-12 с/с, что на два-три порядка выше текущих наблюдательных ограничений. Такое расхождение позволяет предположить, что предположение о форме лагранжиана ( $ℒm = -ρ$ ) может быть несостоятельным, и требует дальнейших исследований для уточнения моделей гравитационного взаимодействия и поиска отклонений от предсказаний общей теории относительности.

Исследование, представленное в данной работе, демонстрирует, как даже незначительные отклонения от общей теории относительности в рамках скалярно-тензорных теорий, таких как Brans-Dicke и Entangled Relativity, могут приводить к существенным последствиям в сильных гравитационных полях. Подобные малые изменения, как показано при численном анализе пост-ньютоновских параметров, резонируют по всей системе, потенциально генерируя дипольные гравитационные волны, что открывает новые возможности для проверки фундаментальных аспектов гравитации. Как писал Альбер Камю: «Всё начинается с малого». Эта фраза находит глубокий отклик в контексте исследования, подчеркивая, что незначительные локальные изменения в фундаментальных параметрах могут порождать колоссальные эффекты в масштабах Вселенной.

Куда Ведет Дорога?

Представленные вычисления параметров пост-ньютоновского приближения в рамках скалярно-тензорных теорий гравитации, безусловно, расширяют горизонты понимания. Однако, следует признать, что точное соответствие между локальными правилами, управляющими этими теориями, и глобальным поведением гравитационных систем не всегда очевидно. Эффект целого, как показывает опыт, часто отличается от простой суммы частей. Полученные отклонения от общей теории относительности в сильных гравитационных полях указывают на необходимость более детального изучения, но не гарантируют открытия «истинной» теории гравитации.

Поиск дипольного гравитационного излучения, предсказанного данными теориями, является логичным следующим шагом. Но даже в случае его обнаружения, следует помнить, что это лишь один из возможных проявлений более сложной реальности. Попытки «управлять» гравитацией, выявлять скрытые переменные, по сути, иллюзорны. Гораздо продуктивнее — наблюдать, фиксировать, и позволять системе эволюционировать согласно своим внутренним законам.

Будущие исследования, вероятно, потребуют более сложных численных методов и, возможно, привлечения альтернативных подходов к моделированию сильных гравитационных полей. Но главное — не забывать о скромности перед лицом фундаментальных вопросов. Ведь в конечном итоге, универсальные законы не нуждаются в архитекторе — они просто возникают.

Оригинал статьи: https://arxiv.org/pdf/2602.11811.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-15 06:04