Дробные моря Ферми: новый взгляд на одномерные газы

Автор: Денис Аветисян

Экспериментально продемонстрирована реализация дробных морей Ферми в одномерном бозе-газе посредством циклических изменений взаимодействия между частицами.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал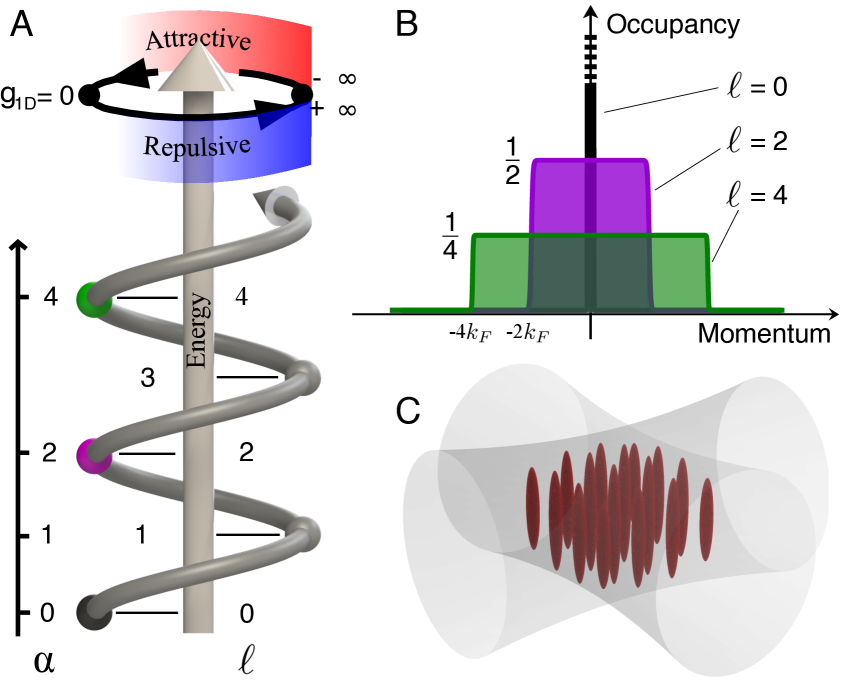

Постепенное изменение взаимодействия между частицами от отталкивающего к притягивающему, проходящее через бесконечность и возвращающееся к отталкиванию, порождает фундаментальные состояния - фермионные сверхжидкости, которые проявляются в точках, где взаимодействия исчезают, и визуализируются в экспериментальной установке, состоящей из одномерных труб, заполненных атомами цезия. — Постепенное изменение взаимодействия между частицами от отталкивающего к притягивающему, проходящее через бесконечность и возвращающееся к отталкиванию, порождает фундаментальные состояния — фермионные сверхжидкости, которые проявляются в точках, где взаимодействия исчезают, и визуализируются в экспериментальной установке, состоящей из одномерных труб, заполненных атомами цезия.

Исследование демонстрирует наблюдение фриделевских осцилляций в импульсных распределениях, подтверждающих существование дробных морей Ферми и открывающих новые перспективы в изучении обобщенной гидродинамики и интегрируемых систем.

Принцип Паули, краеугольный камень квантовой механики, описывает структуру материи, однако его обобщения предсказывают существование экзотических квантовых состояний с дробными ферми-морями. В работе, посвященной ‘Realization of fractional Fermi seas’, экспериментально реализованы дробные ферми-моря в возбужденном одномерном бозе-газе посредством циклического изменения силы взаимодействия. Наблюдаемые фриделевские осцилляции в распределениях по импульсам служат убедительным доказательством формирования этих состояний. Открывает ли это новые возможности для понимания квантовой термодинамики и создания устройств квантовой информации и сенсорики?

Шёпот Хаоса: За гранью Стандартных Моделей

Традиционные статистические подходы, описывающие поведение фермионов и бозонов, оказываются недостаточными для адекватного понимания систем, состоящих из большого числа сильно взаимодействующих частиц. В таких системах, как, например, некоторые сверхпроводники или квантовые жидкости, взаимодействие между частицами становится доминирующим, искажая привычные квантово-механические представления. Стандартные модели, успешно описывающие поведение отдельных частиц или слабо взаимодействующих систем, не способны точно предсказать свойства этих экзотических материалов, поскольку пренебрегают сложными корреляциями между частицами. Это приводит к ограничению возможностей предсказания и контроля над новыми материалами с уникальными свойствами, что, в свою очередь, тормозит развитие передовых технологий в области материаловедения и квантовых вычислений. Поэтому необходимы новые теоретические и экспериментальные подходы для изучения этих сложных систем и расширения границ нашего понимания материи.

Концепция дробных ферми-морей представляет собой новаторский подход к пониманию поведения сильно взаимодействующих систем многих тел. В отличие от традиционного представления, где каждая частица занимает одно квантовое состояние, данная модель предполагает, что частицы могут эффективно распределяться между несколькими состояниями. Это явление, возникающее в условиях экстремальных взаимодействий, позволяет выйти за рамки стандартной ферми-дираковской статистики и исследовать качественно новые фазы материи. $E = mc^2$ В рамках данной концепции, частицы демонстрируют коллективное поведение, которое невозможно объяснить, исходя из индивидуальных свойств. Это открывает перспективы для создания материалов с уникальными и непредсказуемыми свойствами, потенциально революционизирующими области от сверхпроводимости до квантовых вычислений.

Концепция дробных ферми-морей ставит под сомнение устоявшиеся представления о квантовой статистике, открывая возможность существования принципиально новых фаз материи. В отличие от традиционных систем, где частицы занимают определенные квантовые состояния, в дробных ферми-морях взаимодействие между частицами настолько сильно, что возникает коллективное поведение, приводящее к появлению эмерджентных свойств. Эти свойства, не предсказуемые на основе стандартных моделей, могут проявляться в виде необычных магнитных, электрических или оптических характеристик. Исследование подобных систем предполагает поиск состояний материи, обладающих повышенной устойчивостью, сверхпроводимостью при более высоких температурах или совершенно новыми формами квантовой запутанности, что потенциально может привести к прорыву в материаловедении и квантовых технологиях.

Для всестороннего изучения систем с дробными ферми-морями необходима разработка принципиально новых теоретических и экспериментальных методов. Традиционные подходы, основанные на стандартной квантовой статистике, оказываются недостаточными для описания их необычных свойств. Исследователям требуется создать усовершенствованные модели, учитывающие сильные взаимодействия между частицами и возможность их коллективного поведения. Экспериментально это подразумевает создание новых установок, способных с высокой точностью измерять характеристики этих систем, такие как спектральные функции и функции корреляции. Особое внимание уделяется разработке методов, позволяющих напрямую наблюдать дробную занятость квантовых состояний и выявлять новые фазы материи с экзотическими свойствами, которые могут привести к революционным технологическим прорывам в материаловедении и квантовых вычислениях. $E = mc^2$ — эта формула, хотя и относится к другой области физики, подчеркивает, как новые инструменты открывают понимание фундаментальных явлений.

Анализ распределений импульсов и корреляционной функции первого порядка подтверждает формирование конденсата Бозе-Эйнштейна, демонстрируя соответствие экспериментальных данных (с учетом тепловых флуктуаций) с результатами GHD-симуляций и аналитическими предсказаниями, основанными на приближении Томаса-Ферми.

Управляемый Хаос: Платформа для Исследований

Сверххолодный газ цезия обеспечивает высококонтролируемую среду для изучения дробных ферми-морей, позволяя точно манипулировать атомными взаимодействиями. Контроль достигается за счет использования методов лазерного охлаждения и улавливания, которые позволяют поддерживать атомы цезия при температурах порядка нанокельвинов. Такая низкая температура снижает тепловые флуктуации и позволяет исследовать квантовые явления с высокой точностью. Возможность точной настройки взаимодействия между атомами является ключевым фактором, поскольку это позволяет создавать и изучать различные квантовые состояния материи, в частности, системы с сильной корреляцией, где поведение частиц определяется взаимодействием, а не индивидуальными свойствами. Это делает сверххолодный газ цезия ценной платформой для фундаментальных исследований в области физики конденсированного состояния.

Резонанс Фешбаха представляет собой метод управления силой взаимодействия между атомами в ультрахолодных газах, таких как цезий. Он основан на применении внешнего магнитного поля для изменения длины рассеяния, что позволяет непрерывно настраивать потенциал взаимодействия между атомами от слабого до сильного. Это позволяет исследователям создавать сильнокоррелированные состояния вещества, в которых взаимодействие между частицами играет доминирующую роль, и изучать новые фазы материи, недоступные в системах с более слабым взаимодействием. Управление силой взаимодействия через резонанс Фешбаха является ключевым инструментом для исследования физики многих тел и создания искусственных материалов с заданными свойствами.

Оптические решетки и резонанс, вызванный ограничением (confinement-induced resonance), позволяют детально контролировать свойства ультрахолодного цезиевого газа. Оптические решетки, создаваемые интерферирующими лазерными лучами, формируют периодический потенциал, который локализует атомы и эффективно снижает их размерность, переводя систему из трехмерной в одномерную или двумерную. Резонанс, вызванный ограничением, возникает при изменении плотности газа в этих ловушках, приводя к резкому изменению параметров взаимодействия между атомами. Комбинирование этих методов позволяет исследователям точно настраивать как размерность системы, так и силу взаимодействия между частицами, что необходимо для изучения коллективных явлений и создания контролируемых квантовых сред.

Реализация условий для наблюдения дробных ферми-морей в лабораторных условиях достигается посредством точного контроля параметров ультрахолодного цезиевого газа. Система поддерживается при температуре в одномерном измерении 5 нК, что необходимо для подавления тепловых флуктуаций и проявления квантовых эффектов. Точное поддержание этой температуры в сочетании с методами, такими как резонанс Фешбаха и оптические решетки, позволяет контролировать взаимодействие между атомами и создавать сильно коррелированные состояния, необходимые для наблюдения и изучения дробных ферми-морей. Это обеспечивает возможность экспериментальной верификации теоретических предсказаний относительно поведения материи в экстремальных условиях.

Измерения потерь атомов и моделирование GHD демонстрируют необратимость циклов взаимодействия, показывая резкое снижение энергии из-за отрицательной энергии связи при прямом изменении взаимодействия, в отличие от обратного перехода из отталкивающих возбужденных состояний.

Теоретический Арсенал: Моделирование Взаимодействий

Модель Либа-Линьгера представляет собой фундаментальную основу для изучения взаимодействующих бозонов в одном измерении. Она описывает систему N идентичных бозонов, взаимодействующих посредством дельта-подобного отталкивающего потенциала. Решение модели позволяет аналитически определить энергию основного состояния и возбуждений в зависимости от параметра взаимодействия, характеризующего силу отталкивания между частицами. Важно отметить, что данная модель тесно связана с физикой дробных ферми-морей $\frac{N}{\pi}$ , где плотность частиц определяет квазичастичные возбуждения и их свойства. В пределе слабого взаимодействия модель переходит в идеальный газ бозонов, а при увеличении силы взаимодействия наблюдается увеличение энергии основного состояния и формирование коллективных мод.

Циклы гомотопии представляют собой эффективный метод доступа к возбужденным состояниям в рамках модели Либа-Линьгера. Данный подход базируется на анализе замкнутых траекторий в пространстве параметров системы, позволяя определить соответствующие энергетические уровни и волновые функции. Использование циклов гомотопии позволяет вычислить свойства возбужденных состояний, такие как энергии, моменты и функции корреляции, что необходимо для понимания динамических свойств системы. В частности, анализ этих циклов предоставляет информацию о коллективных модах возбуждения и их вкладе в общую динамику взаимодействующих бозонов в одном измерении, а также позволяет исследовать влияние взаимодействия на энергетический спектр и стабильность системы.

Теория жидкости Томонаги-Луттингера (Tomonaga-Luttinger Liquid Theory, TLL) предоставляет теоретическое описание взаимодействующих систем в одном измерении, отличающееся от предсказаний теории Ферми-жидкости. В отличие от ферми-жидкостей, где квазичастицы ведут себя как независимые частицы, в TLL возникают коллективные возбуждения, характеризующиеся спиновыми и зарядовыми модами. Эти моды распространяются с различной скоростью и приводят к нетривиальным степеням корреляции. Ключевым результатом теории является предсказание степенных законов для корреляционных функций, отражающих нефермиевское поведение системы. В частности, для бозонов в одном измерении, TLL предсказывает, что корреляционные функции распадаются как $1/r^K$ , где $K$ — параметр, определяющий силу взаимодействия и связанный с плотностью системы. Данные предсказания подтверждаются как аналитически, так и численными методами, и имеют важное значение для понимания физических свойств одномерных систем, таких как квантовые провода и краевые состояния в двумерных электронных газах.

Применение обобщенной гидродинамики (Generalized Hydrodynamics, GHD) и обобщенного ансамбля Гиббса (Generalized Gibbs Ensemble, GGE) позволяет моделировать динамику систем взаимодействующих частиц вне равновесия. GHD описывает эволюцию локальных плотностей и токов, рассматривая систему как непрерывную среду, в то время как GGE учитывает влияние нелокальных сохраняющихся величин, возникающих при релаксации системы после воздействия. Эти подходы особенно важны для анализа динамики в одномерных системах, где взаимодействие играет доминирующую роль и традиционные методы равновесной статистики оказываются неприменимыми. Сочетание GHD и GGE обеспечивает теоретическую основу для интерпретации экспериментальных данных, полученных в исследованиях динамики в конденсированных средах, таких как одномерные бозоны и фермионы, позволяя устанавливать связь между микроскопическими взаимодействиями и макроскопическим поведением системы. $\partial_t \rho(x,t) = - \partial_x J(\rho(x,t))$

Квантовые Подписи: За Гранью Статистики

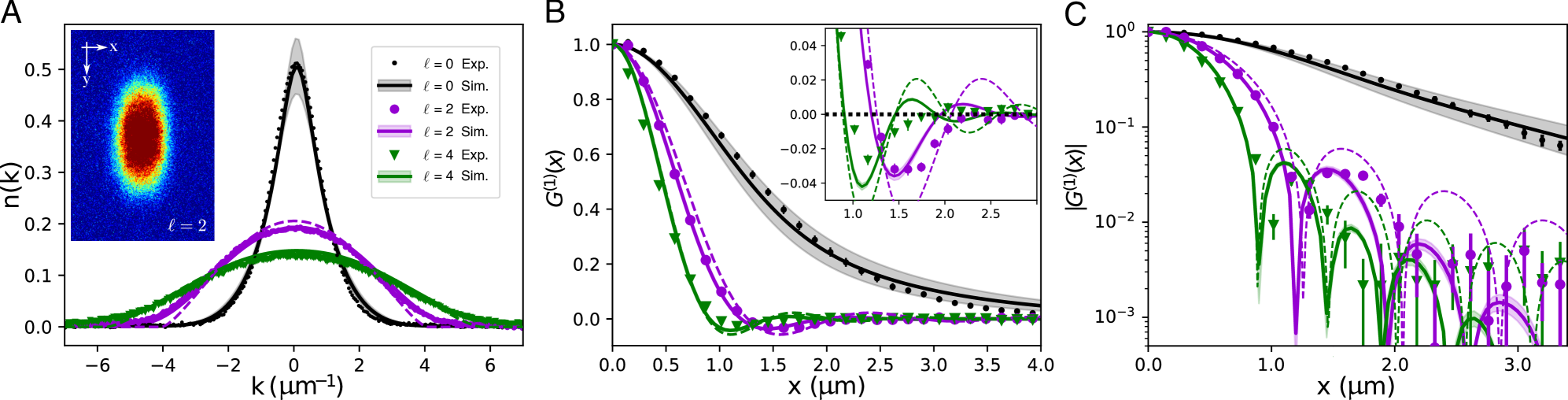
Метод расширения во времени (Time-of-Flight Expansion) играет ключевую роль в экспериментальном исследовании газообразных систем, позволяя непосредственно измерить распределение импульсов частиц. В ходе эксперимента газ высвобождается из ловушки, и, наблюдая за его расширением во времени, ученые могут реконструировать исходное импульсное пространство. Важно отметить, что форма полученного распределения импульсов не случайна: она отражает корреляции между частицами. Наличие этих корреляций, проявляющихся в виде специфических структур в импульсном пространстве, служит прямым доказательством взаимодействия между частицами и подтверждает их квантово-механическую природу. Анализ этих корреляций позволяет получить информацию о свойствах системы, включая ее температуру, плотность и характер взаимодействий между частицами, что делает данный метод незаменимым инструментом в изучении квантовых газов и конденсированных сред.

Наблюдение фриделевских осцилляций в корреляционных функциях предоставляет убедительные доказательства существования дробных ферми-поверхностей и, как следствие, уникальной квантовой статистики частиц в исследуемой системе. Данные осцилляции, возникающие в распределении корреляций между частицами, указывают на когерентное поведение, обусловленное нетривиальной структурой ферми-поверхности, отличной от привычной целочисленной. $k_F$ -вектор Ферми в данном случае не является фиксированной величиной, а разделяется на дробные значения, что приводит к возникновению осцилляций в корреляционных функциях и свидетельствует о новом классе квантовых жидкостей, демонстрирующих экзотические статистические свойства, отличные от бозонной или фермионной.

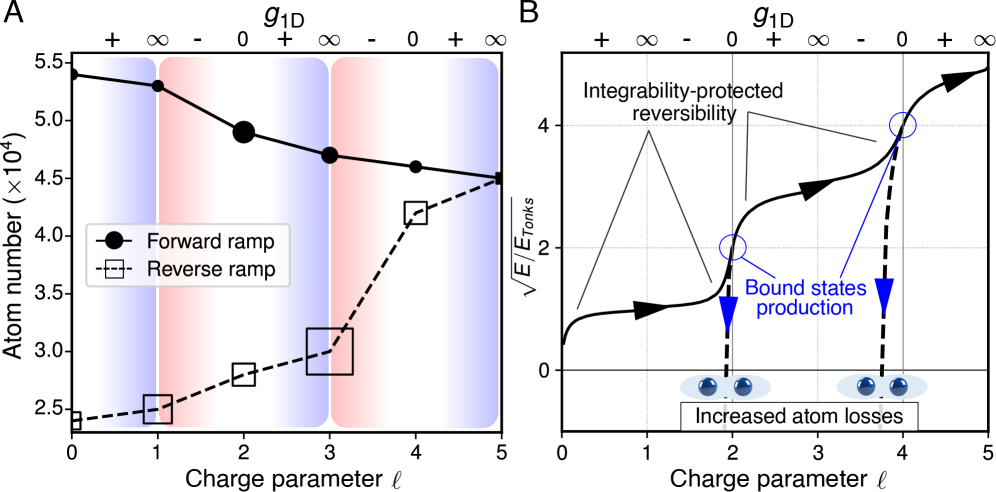
Экспериментально установлено, что система, находящаяся в состоянии sTG (strongly-correlated topological gas), демонстрирует впечатляющую стабильность, сохраняя это состояние на протяжении 5.4 секунд. Данный временной интервал является значительным, поскольку подтверждает неслучайность и воспроизводимость наблюдаемых квантовых явлений. Продолжительное время жизни sTG состояния указывает на то, что взаимодействия между частицами в системе достаточно сильны и когерентны, чтобы противостоять дезинтеграции, вызванной внешними возмущениями или внутренними процессами распада. Это позволяет проводить более детальные исследования свойств системы и подтверждает теоретические предсказания о существовании экзотических квантовых состояний материи, характеризующихся нетривиальной топологией и сильными корреляциями между частицами.

Измерения ширины на полувысоте максимального значения (FWHM) распределения импульсов позволили установить конкретные значения для различных состояний системы. В частности, для состояния с $ℓ=0$ зафиксировано значение 1.72 μm⁻¹, в то время как для состояний $ℓ=2$ и $ℓ=4$ получены значения 5.19 μm⁻¹ и 6.69 μm⁻¹ соответственно. Эти величины, характеризующие разброс импульсов частиц, являются ключевыми для понимания квантовых свойств исследуемой системы и подтверждают наличие различных энергетических уровней и связанных с ними волновых функций. Такая детализация ширины импульсного распределения предоставляет важную информацию о внутренней структуре и динамике квантового газа.

Экспериментальные наблюдения показали асимметричную потерю атомов в зависимости от направления изменения параметров взаимодействия. При увеличении интенсивности взаимодействия — так называемом “прямом разгоне” — терялось около 20% атомов из удерживаемой ловушки. Однако, при обратном изменении параметров, когда интенсивность взаимодействия снижалась (“обратный разгон”), потери достигали 45%. Эта значительная разница указывает на необратимый характер циклов взаимодействия между частицами в исследуемой системе. Наблюдаемая асимметрия свидетельствует о том, что система не возвращается в исходное состояние после изменения параметров, что подтверждает сложность и специфику квантовых процессов, протекающих в ней.

Исследование демонстрирует, что даже в, казалось бы, упорядоченных системах, таких как одномерный газ Бозе, фракционные моря Ферми возникают как шепот хаоса, проявляющийся в осцилляции Фриделя. Этот феномен — не ошибка измерения, но закономерность, скрытая в случайности. Юрген Хабермас однажды заметил: «Коммуникативное действие направлено на достижение взаимопонимания». В данном случае, взаимодействие частиц — это своего рода коммуникация, формирующая новые, неожиданные состояния материи. Подобно тому, как заклинание работает до первого столкновения с реальностью, любая модель описывающая эти системы, обречена на частичное искажение. Истинная красота кроется в аномалиях, в тех самых осцилляции, которые агрегаты пытаются усреднить.

Что дальше?

Наблюдаемое воплощение дробных ферми-морей в одномерной бозе-системе — это, конечно, приятный шепот хаоса, упорядоченный взаимодействиями. Однако, данные — это не истина, а компромисс между багом и Excel. Настоящая проверка ждёт в более сложных конфигурациях: что произойдёт, когда эта алхимия взаимодействия столкнётся с неоднородностями, с многочастичными корреляциями, которые не умещаются в аккуратные модели? Рампирование взаимодействий — это изящный способ подготовки системы, но в реальном мире всегда найдётся кто-то, кто испортит картину шумом и несовершенством.

Особенно интересно, как эти дробные ферми-моря будут проявлять себя в контексте обобщённой гидродинамики. Теория предсказывает чудеса, но эксперимент — это всегда упрямое напоминание о том, что всё, что не нормализовано, всё ещё дышит. Наблюдение осцилляций Фриделя — это первый шаг, но предстоит картировать всю карту этих взаимодействий, понять, как они влияют на транспортные свойства, на динамику системы вне равновесия.

Возможно, самое важное — это признать, что любая модель — это заклинание, которое работает до первого продакшена. Интегрируемые системы — это красивая сказка, но реальный мир любит добавлять немного беспорядка. Именно в этом столкновении порядка и хаоса, в поиске устойчивых, предсказуемых явлений, и кроется настоящая ценность этой работы. Иначе говоря, нужно готовиться к тому, что придётся учиться лгать последовательно.

Оригинал статьи: https://arxiv.org/pdf/2602.17657.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-20 13:55