Автор: Денис Аветисян
Теоретическое исследование предсказывает возможность воздействия на магнитные состояния в слоистых материалах с помощью света, благодаря ранее неизвестному эффекту связи между электрическими и спиновыми степенями свободы.
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-канал
В работе показано существование рамановской силы, связывающей электрическое поле со сдвиговыми фононами в фрустрированном двумерном магнетике.
В то время как взаимодействие света с магнитными степенями свободы обычно рассматривается через диэлектрические или магнитные каналы, природа этого взаимодействия в сложных многослойных системах остается не до конца изученной. В работе «Магнитоэлектрическая сила Рамана на сдвиговых фононах во фрустрированном слоистом двумерном магнетике» представлен теоретический анализ возникновения силы Рамана, связывающей электрическое поле с коллективными спиновыми возбуждениями в слоистом бислойном магнетике. Показано, что благодаря спин-токовому взаимодействию и магнитоупругой связи, электрическое поле может эффективно возбуждать сдвиговые фононы посредством промежуточного взаимодействия с магнонами. Открывает ли это путь к когерентному управлению магнитным состоянием материалов с помощью света и какие новые функциональные возможности могут быть реализованы в многослойных вандерваальсовых гетероструктурах?
Слоистые материалы: платформа для когерентного управления фононами
Материалы Ван-дер-Ваальса, такие как дихалькогениды переходных металлов и двуслойный графен, представляют собой уникальную платформу для исследований благодаря своей слоистой структуре и слабому межслоевому взаимодействию. Эта особенность позволяет эффективно разделять и контролировать электронные и фононные свойства каждого слоя, открывая возможности для создания новых наноразмерных устройств. Слабое сцепление между слоями минимизирует рассеяние фононов, что способствует поддержанию когерентности и длительного времени жизни колебаний решетки. Такая архитектура позволяет настраивать теплопроводность и управлять потоком энергии на наноуровне, что крайне важно для разработки эффективных термоэлектрических генераторов и высокопроизводительных электронных компонентов. Изучение этих материалов открывает новые горизонты в области нанофононики и материаловедения.
В слоистых материалах, таких как дихалькогениды переходных металлов и двуслойный графен, наблюдается существование когерентных оптических фононов — квантов колебаний кристаллической решетки, сохраняющих фазовую связь. Эти коллективные колебания играют ключевую роль в управлении потоком энергии на наноуровне, поскольку позволяют эффективно переносить и направлять тепло, не рассеивая его. \hbar \omega — энергия фонона, где \hbar — постоянная Планка, а ω — частота колебаний. Контроль над когерентностью фононов открывает перспективы для создания новых наноэлектронных устройств с улучшенными тепловыми характеристиками и повышенной эффективностью, а также для разработки принципиально новых подходов к термоуправлению в микро- и наноэлектронике.
Механизмы возбуждения: от импульсного к смещающему
Когерентные фононы могут возбуждаться двумя основными механизмами: импульсивным возбуждением (ImpulsiveExcitation) и смещающим возбуждением (DisplaciveExcitation). Импульсивное возбуждение создает колебания вокруг начального положения равновесия, не изменяя само это положение. В отличие от него, смещающее возбуждение приводит к сдвигу положения равновесия, вызывая устойчивое смещение структуры материала. Оба механизма приводят к возникновению когерентных колебаний решетки, характеризующихся определенной частотой и волновым вектором, и являются фундаментальными для понимания динамики фононов в твердых телах.
Оба механизма возбуждения — импульсивный и смещающий — эффективно приводят в движение моды сдвиговых фононов ρ. Эффективность этого процесса особенно возрастает при наличии сдвига слоев в материале. Сдвиг слоев создает дополнительное напряжение, которое усиливает взаимодействие между возбуждением и модами сдвиговых фононов, что приводит к более выраженным колебаниям и, как следствие, к более заметным экспериментальным проявлениям этих эффектов. В материалах с выраженной слоистой структурой этот эффект становится определяющим фактором в динамике фононов.
Возбуждения, происходящие в решетке материала, не ограничиваются теоретическими построениями и проявляются в измеримых откликах, что делает их критически важными для понимания динамики фононов. Такие отклики могут быть зарегистрированы с помощью различных экспериментальных методов, включая неэластичное рассеяние нейтронов и рентгеновское рассеяние, позволяя непосредственно наблюдать спектр фононов и их взаимодействие с другими квазичастицами. Анализ этих измеримых откликов предоставляет информацию о частотах, длинах волн и векторах поляризации фононов, а также о факторах, влияющих на их рассеяние и затухание. Полученные данные необходимы для разработки и валидации теоретических моделей, описывающих теплопроводность, упругие свойства и другие важные характеристики материалов.
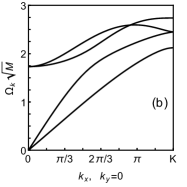
Управление когерентностью: стимулированное рассеяние Рамана и сила Рамана
Стимулированное рассеяние Рамана (СРР) представляет собой эффективный метод возбуждения когерентных оптических фононов, позволяющий точно контролировать их амплитуду и фазу. В отличие от спонтанного рассеяния, СРР использует мощный накачивающий лазер, который когерентно взаимодействует с оптическими фононами, усиливая их и поддерживая когерентность. Это достигается за счет нелинейного оптического взаимодействия, где фотоны накачки теряют энергию, передавая её фононам. Точное управление параметрами лазера, такими как частота и интенсивность, позволяет регулировать как амплитуду, так и фазу возбужденных фононов, открывая возможности для управления тепловыми свойствами материалов и создания когерентных акустических волн. ω_{phonon} = ω_{laser} - ω_{scattered}.
В основе возбуждения когерентных фононов посредством стимулированного рассеяния Рамана лежит сила Рамана, действующая непосредственно на решетные колебания. Данная сила пропорциональна приложенному электрическому полю E и диэлектрической восприимчивости материала χ, что определяет эффективность взаимодействия света с фононами. В математической форме сила Рамана выражается как F_R ∝ Eχ. Таким образом, увеличение напряженности электрического поля или диэлектрической восприимчивости приводит к увеличению силы, воздействующей на фононы и, следовательно, к более эффективному возбуждению когерентных колебаний решетки.
Расчеты показывают, что величина силы Рамана обратно пропорциональна \propto 1/\Gamma , где Γ представляет собой скорость затухания магнонов. Это указывает на высокую чувствительность процесса к качеству материала и параметрам, определяющим затухание магнонов. Увеличение скорости затухания приводит к ослаблению силы Рамана и, следовательно, к снижению эффективности возбуждения когерентных оптических фононов. Таким образом, контроль качества материала и минимизация Γ являются ключевыми факторами для достижения эффективного управления когерентными колебаниями.
Расчеты показывают, что спектральный вес силы Рамана остается значительным до значения, равного удвоенному максимуму ϵ_k, где ϵ_k представляет собой энергию фонона. Это определяет релевантный энергетический масштаб для эффективного возбуждения когерентных колебаний в материале. Превышение данного порога приводит к существенному снижению эффективности воздействия силы Рамана на фононы, делая невозможным эффективное управление их амплитудой и фазой. Таким образом, величина 2*max(ϵ_k) является критическим параметром при разработке схем управления когерентными оптическими фононами посредством стимулированного рассеяния Рамана.
Магнитоэлектрическое связывание и фрустрированный магнетизм
Никельдииодид, обладающий слоистой кристаллической структурой, демонстрирует некомменсуратный спиральный магнитный порядок, являющийся следствием фрустрированного магнетизма. В данном материале, взаимодействие между магнитными моментами в слоях не приводит к простому упорядочению, а порождает спиральную структуру, в которой магнитные моменты постепенно поворачиваются в плоскости слоев. Эта фрустрация возникает из-за геометрии кристаллической решетки и характера обменного взаимодействия между ионами никеля. Некомменсуратность спирального порядка означает, что период спирали не соизмерим с периодом кристаллической решетки, что обуславливает уникальные физические свойства материала и открывает возможности для создания новых мультиферроиков.
Взаимодействие между магнитным упорядочением и кристаллической решеткой в некоторых материалах приводит к особому типу связи, описываемому сцеплением Кацура-Нагаоса-Балацки. Данное сцепление является основой для возникновения так называемой мультиферроичности типа II, где спонтанная поляризация возникает как следствие магнитного порядка. Ключевым проявлением этого феномена является магнитоэлектрический эффект — способность материала генерировать электрическую поляризацию под воздействием магнитного поля и наоборот. Данное явление открывает перспективы для создания принципиально новых устройств памяти и сенсоров, использующих спиновые токи для управления электрическими полями, и наоборот, что делает подобные материалы предметом интенсивных исследований в области конденсированного состояния.
Представленная работа описывает теоретическую модель, предсказывающую сильно анизотропный отклик в спектрах комбинационного рассеяния света, зависящий от вектора спиральной укладки. Согласно разработанной теории, интенсивность и поляризация комбинационного сигнала напрямую связаны с направлением и величиной вектора \mathbf{q} , характеризующего спиральную магнитную структуру. Данная зависимость позволяет использовать спектроскопию комбинационного рассеяния как чувствительный метод для определения параметров спиральной укладки и контроля качества материалов с подобной структурой, в частности, никелдииодида. Полученные теоретические предсказания открывают возможности для разработки новых методов исследования и управления мультиферроиками, использующих взаимодействие между спиновой и кристаллической структурой.
Теоретические расчеты показали обратную зависимость между величиной вынужденной силы Рамана и скоростью затухания магнонов Γ. Данное соотношение подчеркивает высокую чувствительность этого эффекта к качеству кристаллической структуры материала. Более высокая скорость затухания магнонов, обусловленная дефектами или примесями, приводит к ослаблению вынужденной силы Рамана, что делает ее потенциальным инструментом для неразрушающей оценки однородности и дефектности никелдииодида. В результате, анализ спектра вынужденной силы Рамана может предоставить ценную информацию о внутренних характеристиках материала и оптимизации его свойств для практического применения в многофункциональных устройствах.
Теория, конечно, элегантна — продемонстрировать рамановскую силу, связывающую электрические поля со спиновыми степенями свободы в слоистом мультиферроике. Звучит как прорыв, способствующий контролю магнитных состояний светом. Но давайте будем реалистами. За этим, несомненно, последует гора коммитов, патчей и, скорее всего, необходимость переписывать половину симуляций, когда выяснится, что учёт ван-дер-ваальсовых взаимодействий был недостаточно точным. Как всегда, красивая математика столкнётся с суровой реальностью производственного процесса. Впрочем, сейчас это назовут AI и получат инвестиции. Как заметил Людвиг Витгенштейн: «Предел моего языка есть предел моего мира». И в данном случае, предел симуляций быстро станет очевиден, когда теория столкнётся с несовершенством материалов.
Что дальше?
Теоретическое предсказание рамановской силы, связывающей электрические поля со спиновыми степенями свободы, конечно, элегантно. Однако, как показывает опыт, переход от элегантной теории к стабильной системе — задача нетривиальная. Разумеется, в реальных материалах всегда найдется какой-нибудь эффект, который сломает идеальную модель. Дислокации, дефекты, тепловые флуктуации — список можно продолжать бесконечно. Впрочем, если система стабильно падает — значит, хотя бы последовательна.
Наиболее очевидный путь — экспериментальная верификация предсказанного эффекта. Но даже если рамановская сила будет обнаружена, вопрос о практическом применении остаётся открытым. Контроль над магнитными состояниями светом — звучит красиво, но для создания реального устройства потребуется решить множество технических проблем. Квантовые компьютеры, например, тоже обещали революцию, а пока что это, скорее, дорогостоящий исследовательский инструмент.
В конечном счёте, данная работа — это ещё один кирпичик в фундаменте, который, возможно, когда-нибудь станет зданием. Или просто окажется кучей камней. В любом случае, не стоит забывать, что мы не пишем код — мы просто оставляем комментарии будущим археологам, которые будут пытаться понять, что здесь происходило.
Оригинал статьи: https://arxiv.org/pdf/2602.16785.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Решение головоломки с паролем Absolum в Yeldrim.
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- YAPYAP Список заклинаний
- Все коды в Poppy Playtime Глава 4
- Прогнозы криптовалюты MYX: информация о ценах на MYX
- Доллар обгонит вьетнамский донг? Эксперты раскрыли неожиданный сценарий
- Акции VTBR. Банк ВТБ: прогноз акций.
- Лучшие шаблоны дивизий в Hearts Of Iron 4
- Объяснение каждого Таргариена в «Рыцаре семи королевств»
- Нечестивцам нет покоя: как получить старый ключ от коттеджа
2026-02-22 17:52