Автор: Денис Аветисян
Новое исследование раскрывает механизмы управления колебаниями в наноосцилляторах, основанных на антиферромагнетиках с не-коллинеарной структурой.
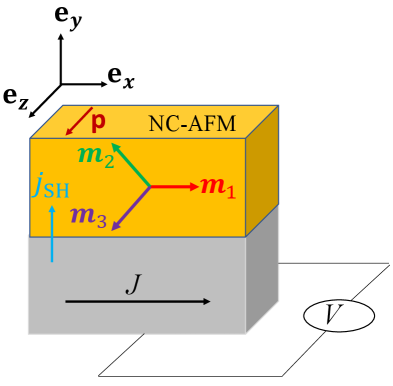
Анализ влияния анизотропии и обменного взаимодействия на гистерезис и устойчивые состояния в спин-торковых наноосцилляторах.
Несмотря на значительный прогресс в области спинтроники, динамика некомпланарных антиферромагнитных спин-торковых осцилляторов (NC-AFM STO) остается недостаточно изученной. В работе ‘Hysteretic Excitation in Non-collinear Antiferromagnetic Spin-Torque Oscillators: A Terminal Velocity Motion Perspective’ предложена аналитическая модель, объединяющая спиновую динамику в рамках формализма пуассоновских скобок и описывающая переход от быстрых переходных процессов к стабильным осцилляторным состояниям. Показано, что ключевую роль в формировании этих состояний играют анизотропия и обменное взаимодействие, определяющие гистеретические эффекты и фазовую диаграмму системы. Возможно ли, используя предложенный подход, разработать новые, более эффективные спин-торковые наноосцилляторы с заданными характеристиками?
Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.
Бесплатный телеграм-каналАнтиферромагнетики: Танец Спинов и Сложность Управления
Антиферромагнетики представляют собой перспективные материалы для создания энергоэффективных спинтронных устройств, однако полноценная реализация этого потенциала требует глубокого понимания их динамического отклика. В отличие от ферромагнетиков, где спины упорядочены параллельно, в антиферромагнетиках спины соседних атомов ориентированы антипараллельно, что приводит к уникальным свойствам и сложностям в управлении. Исследование того, как антиферромагнитные структуры реагируют на внешние воздействия, такие как магнитные поля или импульсы тока, является ключевым для разработки новых типов запоминающих устройств и логических элементов с минимальным энергопотреблением. Изучение временных характеристик переключения намагниченности, скорости отклика и механизмов релаксации в антиферромагнетиках позволит оптимизировать их характеристики и создать принципиально новые спинтронные технологии.
Поведение антиферромагнетиков при переключении магнитных состояний определяется сложным взаимодействием анизотропии — предпочтительной ориентации магнитных моментов — и внешних воздействий, таких как магнитное поле или ток. Это взаимодействие не является простым и линейным; различные типы анизотропии — кристаллическая, поверхностная, вызванная напряжением — конкурируют друг с другом, формируя энергетический ландшафт, в котором происходит переключение. Для адекватного анализа требуется учитывать не только величину внешнего воздействия, но и его направление относительно кристаллической структуры и внутренних анизотропий. Игнорирование этих нюансов может привести к неверной интерпретации результатов и затруднить разработку эффективных устройств спинтроники на основе антиферромагнетиков. Таким образом, детальное исследование этой взаимосвязи является ключевым для понимания и управления переключением состояний в антиферромагнетиках.
Частица в Магнитном Поле: Модель Движения Антиферромагнетика
Динамика системы может быть эффективно описана с использованием модели движения с постоянной скоростью, рассматривающей магнитный момент как частицу с эффективной массой. В данном подходе, сложное взаимодействие магнитных моментов преобразуется в эквивалентную механическую систему, где на “частицу” действуют различные силы. Эффективная масса учитывает все внутренние взаимодействия, влияющие на движение магнитного момента, позволяя описывать его динамику как движение частицы под действием этих сил. Данная модель позволяет упростить анализ и прогнозирование поведения магнитных моментов в различных условиях, представляя собой удобный инструмент для моделирования динамики антиферромагнетиков.
Данный подход упрощает анализ динамики антиферромагнетика путем сопоставления сложных магнитных взаимодействий с хорошо изученной механической моделью. В рамках этой модели, магнитные моменты рассматриваются как частицы, подверженные воздействию различных сил. В частности, взаимодействие между магнитными моментами преобразуется в эффективные силы, действующие на эти «частицы», что позволяет применить стандартные методы механики для расчета их движения и динамического поведения. Такое преобразование облегчает понимание вклада каждой силы в общую динамику системы и позволяет более эффективно исследовать процессы, такие как переключение намагниченности и прецессия.
Подтверждение адекватности предложенной модели, рассматривающей динамику антиферромагнетика через движение частицы, получено путем сопоставления результатов с данными макроспиновых симуляций. Соглашение между аналитическим описанием и численными расчетами демонстрирует корректность упрощения, позволяющего эффективно моделировать сложные магнитные взаимодействия. Критическая плотность тока, при которой наблюдается существенное изменение динамики, составляет 0.3754 \times 10^9 А/см2, что подтверждается как аналитическим выводом, так и результатами симуляций.
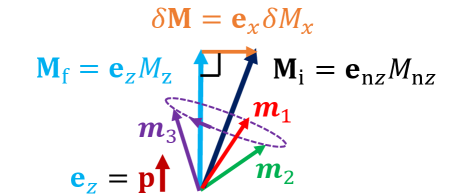
Симметрии и Движение: Математический Фундамент Антиферромагнетизма
Гамильтонов анализ, подкрепленный формализмом пуассоновских скобок, представляет собой эффективный инструмент для исследования непрерывных симметрий системы. В рамках этого подхода, динамические переменные системы описываются через гамильтониан H, а эволюция системы во времени определяется уравнениями Гамильтона. Пуассоновы скобки {A, B} = \sum_{i} (\frac{\partial A}{\partial q_i} \frac{\partial B}{\partial p_i} - \frac{\partial A}{\partial p_i} \frac{\partial B}{\partial q_i}), где q_i и p_i — канонические координаты и импульсы, позволяют определить, какие величины сохраняются при непрерывных преобразованиях координат. Сохраняющиеся величины соответствуют генераторам симметрии, а анализ пуассоновских скобок с этими генераторами выявляет алгебраическую структуру симметрий системы, что необходимо для понимания ее фундаментальных свойств и предсказания ее поведения.
Уравнение Ландау-Лифшица-Гильбера (LLG) описывает эволюцию подрешетничной намагниченности и предоставляет детальное описание динамики системы. Данное уравнение представляет собой векторное уравнение движения, которое учитывает как прецессию намагниченности под действием эффективного поля, так и эффект демпфирования, вызывающий релаксацию намагниченности к состоянию равновесия. Математически, уравнение LLG записывается как \frac{d\mathbf{m}}{dt} = -\gamma \mathbf{m} \times \mathbf{H}_{eff} + \alpha (\mathbf{H}_{eff} \times \mathbf{m})\$, где \mathbf{m} — вектор намагниченности, γ — гиромагнитное отношение, \mathbf{H}_{eff} — эффективное магнитное поле, а α — параметр демпфирования. Включение демпфирующего члена необходимо для учета диссипативных процессов, возникающих в реальных материалах, и обеспечивает стабильность решения.
Инжекция спин-орбитального момента (SOT) посредством слоя тяжелого металла обеспечивает внешний контроль над намагниченностью, позволяя переводить систему в определенные состояния. SOT возникает из-за спин-зависимого рассеяния электронов на интерфейсе между тяжелым металлом и ферромагнитным слоем. Этот эффект приводит к возникновению момента силы, действующего на намагниченность, который может преодолеть анизотропию и переключать ее направление. Эффективность SOT зависит от характеристик используемого тяжелого металла (например, платины, вольфрама) и параметров интерфейса, включая толщину слоев и качество их контакта. Внешний контроль намагниченности посредством SOT позволяет реализовывать различные функциональные возможности, включая переключение намагниченности, управление доменами и создание спиновых волн.
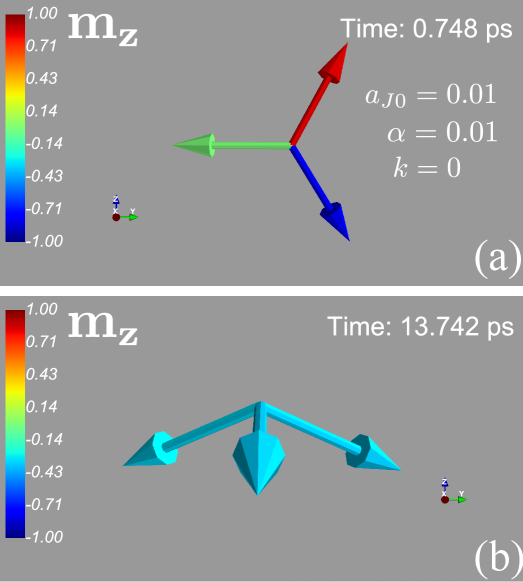
От Теории к Предсказанию: Проверка и Исследование Антиферромагнетизма
Макроскопические симуляции были проведены для подтверждения адекватности разработанной модели движения при достижении терминальной скорости. Полученные результаты демонстрируют высокую степень соответствия между теоретическими предсказаниями аналитического подхода и численными данными, полученными в ходе моделирования. Такое совпадение подтверждает, что предложенная аналитическая модель способна точно описывать динамику системы, предсказывая ее поведение в сложных условиях. Валидация модели с помощью симуляций позволяет уверенно использовать ее для дальнейших исследований и прогнозирования характеристик подобных систем, а также служит основой для разработки более точных и эффективных алгоритмов управления.
Численные моделирования выявили появление самовозбуждающихся импульсов, обусловленных сложным взаимодействием анизотропии материала и неоднородности профилей скорости. Эти импульсы возникают как результат резонансного поведения системы, когда небольшие возмущения усиливаются за счет специфической комбинации свойств материала и кинетики движения. Анализ показывает, что анизотропия создает предпочтительные направления для распространения возбуждений, а неоднородность профилей скорости способствует их локализации и усилению. В результате возникает самоподдерживающийся процесс, приводящий к формированию кратковременных, но интенсивных всплесков активности, которые могут существенно влиять на общие характеристики системы и ее динамическое поведение. Данный феномен представляет значительный интерес для понимания механизмов нелинейной динамики в различных физических системах.
Исследования показали, что критическая плотность тока, определяющая порог гистеретического возбуждения, успешно предсказана как аналитическими, так и численными методами. Полученные результаты демонстрируют высокую степень согласованности, подтверждая значение в 0.3754 \times 10^9 А/см². Важно отметить, что существует верхняя граница этого параметра, достигающая 3.0339 \times 10^9 А/см², после превышения которой наблюдается существенное изменение характеристик системы. Такое точное совпадение между теоретическими расчётами и результатами моделирования подтверждает надёжность используемого подхода и позволяет прогнозировать поведение системы в различных условиях, что является важным шагом для дальнейших исследований и практического применения.
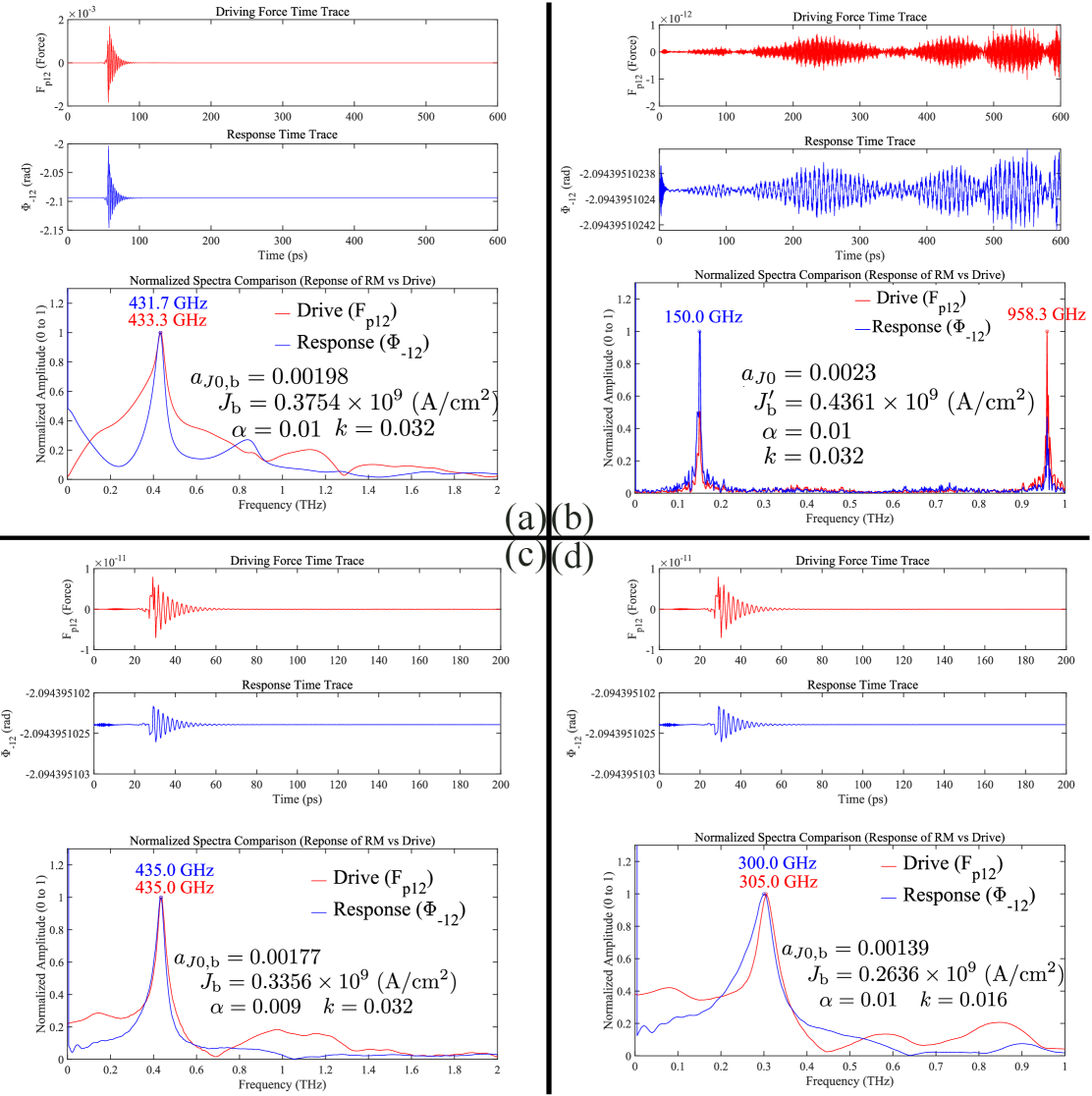
Данная работа, углубляясь в динамику спин-торковых наноосцилляторов в не-коллинеарных антиферромагнетиках, демонстрирует, как ключевые параметры, такие как одноосная анизотропия и обменное взаимодействие, определяют стабильные колебательные состояния и гистерезис. Этот анализ, требующий строгой математической формализации упрощений модели, перекликается с глубоким пониманием границ познания. Как однажды заметил Карл Саган: «Мы — звездная пыль, стремящаяся понять себя». Именно такое стремление к пониманию лежит в основе исследования, где каждая теоретическая конструкция, подобно горизонту событий, может скрывать новые, неожиданные открытия, заставляя пересматривать устоявшиеся представления о физических процессах.
Что дальше?
Представленная работа, тщательно разбирая динамику спин-торковых нано-осцилляторов в не-коллинеарных антиферромагнетиках, лишь обнажает глубину нерешенных вопросов. Удобно, конечно, строить аналитические рамки, но стоит помнить, что любая модель — это всего лишь приближение, а реальность, как известно, всегда сложнее. Особенно когда речь идет о мире спинов, где даже малейшие флуктуации могут привести к непредсказуемым последствиям. Иначе говоря, горизонт событий в микромире тоже существует.
Особое внимание, вероятно, следует уделить исследованию влияния более сложных видов анизотропии и обменного взаимодействия. Простота, хоть и элегантна, но вряд ли отражает истинную сложность физических процессов. Попытки включить в модель эффекты, выходящие за рамки текущего рассмотрения, могут оказаться плодотворными, но, несомненно, усложнят задачу. Впрочем, разве не в этом и заключается вся прелесть науки — в постоянном стремлении к усложнению?
В конечном счете, данная работа — это не столько ответ, сколько приглашение к дальнейшим исследованиям. Антиферромагнетики, как и черные дыры, — лучшие учителя смирения. Они демонстрируют, что не всё поддается контролю, и что даже самые совершенные теории могут оказаться несостоятельными перед лицом реальности. И это прекрасно.
Оригинал статьи: https://arxiv.org/pdf/2601.16000.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Решение головоломки с паролем Absolum в Yeldrim.
- Прогнозы криптовалюты AXS: информация о ценах на AXS
- Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip
- Откровенные заметки, слитые стримером Lacari, привели к его бану на Twitch и Kick.
- YAPYAP Список заклинаний
- The Planet Crafter: полное руководство по картам и биомам
- 15 лучших законченных серий манхвы, которые стоит прочитать, в рейтинге
- Где находится точка эвакуации «Туннель контрабандистов» на локации «Интерчейндж» в Escape from Tarkov?
- Все рецепты культистского круга в Escape from Tarkov
- Лучшие шаблоны дивизий в Hearts Of Iron 4
2026-01-24 10:32