Экзотические квазичастицы: Подтверждение существования одномерных анионов
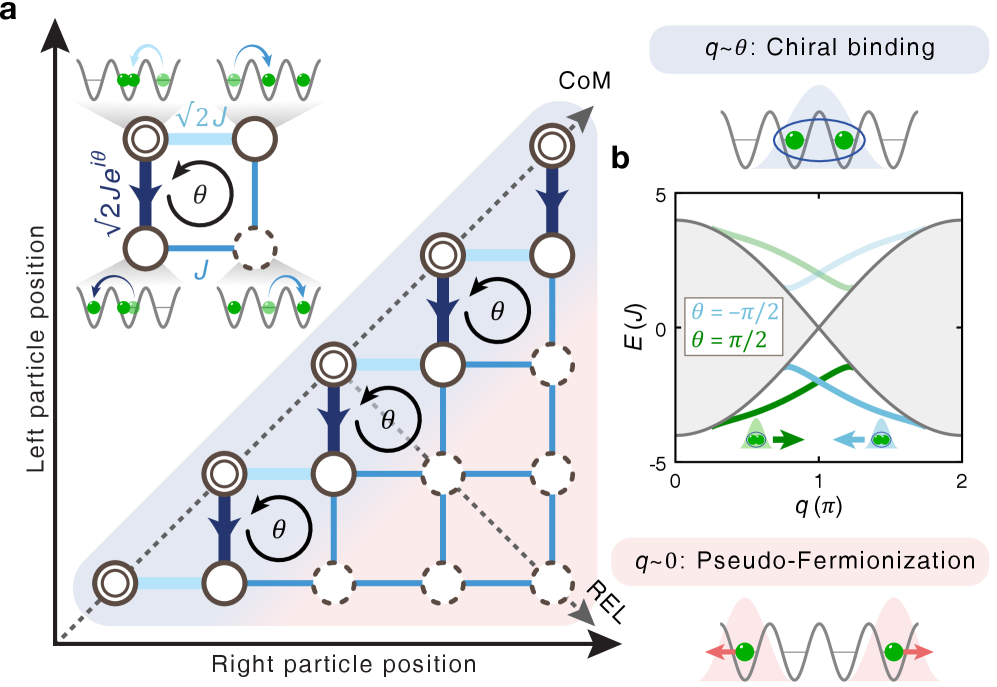
Новое исследование демонстрирует создание и наблюдение уникальных квазичастиц — одномерных анионов — и подтверждает их необычную квантовую статистику.

Новое исследование демонстрирует создание и наблюдение уникальных квазичастиц — одномерных анионов — и подтверждает их необычную квантовую статистику.
![Поведение однопетлевого коэффициента для энергетической щели двойной потенциальной ямы (слева) и для мнимой части кубической потенциальной ямы (справа) демонстрирует сингулярности при [latex]h = h_c[/latex], после чего при [latex]h > h_c[/latex] наблюдается осцилляторное поведение, подавляющее туннелирование в определенных точках, что указывает на критическую зависимость этих систем от величины параметра [latex]h[/latex].](https://arxiv.org/html/2602.20576v1/x33.png)
Новое исследование показывает, как деформация квантовомеханических систем может подавлять туннелирование частиц, открывая неожиданные связи с математической физикой и теорией суперсимметрии.
Новое теоретическое исследование раскрывает, как внутренние свойства частиц влияют на их поведение в искривленных пространствах-временах, предсказывая неожиданные эффекты в гравитационных квантовых интерферометрах.
![Анализ фазовых сдвигов в процессах, включающих гипероны, позволил уточнить разницу между слабыми и сильными фазами [latex] (\delta_{P}-\delta_{S})_{\Xi^{-}} [/latex] и [latex] (\xi_{P}-\xi_{S})_{\Xi^{-}} [/latex], результаты, представленные в данной работе, согласуются с предыдущими измерениями коллаборации BESIII по распаду [latex] J/\psi [/latex] и отличаются от теоретических предсказаний Стандартной модели, что указывает на потенциальные отклонения от неё и необходимость дальнейшего исследования сильных взаимодействий адронов.](https://arxiv.org/html/2602.20524v1/x6.png)
Исследование распадов гиперонов позволило получить наиболее точные на сегодняшний день измерения разности фаз, проливающие свет на фундаментальную проблему исчезновения антиматерии.
Исследователи впервые наблюдали последовательные квантовые осцилляции, вызванные мини-ландоевскими полосами в трехмерном дираковском полупроводнике ZrTe5, открывая новые перспективы в понимании квантовых явлений.
![Вследствие квадратичного взаимодействия аксионов и фермионов, плотные недра Земли изменяют эффективную массу аксионов, создавая эффект, аналогичный распространению света между средами с различным показателем преломления, что приводит к значительному усилению градиента аксионного поля на поверхности планеты и открывает возможности для высокочувствительного комагнометрического детектирования, использующего самокомпенсацию для подавления внешних магнитных помех и считывания прецессии ядер, вызванной градиентом аксионного поля, при выбранных параметрах [latex]m_{a}/2\pi = 1~\mathrm{Hz}[/latex] и [latex]f_{a} = 10^{13.5}~\mathrm{GeV}[/latex], где усиление градиента масштабируется как [latex]1/(kR_{\mathrm{E}})\times\left((f_{a})^{c}/f_{a}\right)^{2}[/latex], при этом амплитуда поля остаётся практически неизменной, а эффект быстро затухает как внутри, так и за пределами Земли.](https://arxiv.org/html/2602.20260v1/x1.png)
Ученые разработали инновационный метод поиска аксионов — частиц, претендующих на роль тёмной материи, используя особенности земного вещества для усиления сигнала.
![На графиках демонстрируется, как неопределённость [latex]\Delta q \Delta_{q}[/latex] меняется в зависимости от параметра [latex]\lambda k(s)[/latex], при значениях 0.1, 0.3, 0.49 и 0.499, показывая, что даже незначительные изменения этого параметра могут приводить к существенным изменениям неопределённости, при этом поправки медленного переката игнорируются.](https://arxiv.org/html/2602.20734v1/x2.png)
Исследование предлагает механизм усиления примордиальных гравитационных волн за счет квантовой запутанности, что может открыть путь к наблюдению квантовых эффектов в космологии.
![В исследуемых алтермагнитных структурах, таких как циркулярные доменные стенки и скайрионы, возникает эффективное спин-орбитальное взаимодействие, обусловленное градиентом фазы и приводящее к расщеплению энергетических уровней [latex]E_{\pm}(\boldsymbol{p}) = \mu[/latex], причем отсутствие узлов в расщеплении для скайрионов объясняется совместным вкладом градиентов [latex]\nabla\theta[/latex] и [latex]\sin\theta\nabla\phi[/latex] в эффективный член спин-орбитального взаимодействия [latex]\boldsymbol{\mathtt{g}}_{\boldsymbol{p}} \propto \boldsymbol{p} \cdot \nabla \phi[/latex].](https://arxiv.org/html/2602.20236v1/x5.png)
Исследование открывает неожиданные электромагнитные и геометрические эффекты, возникающие в материалах с альтернативным магнетизмом, что может привести к принципиально новым способам управления спином.
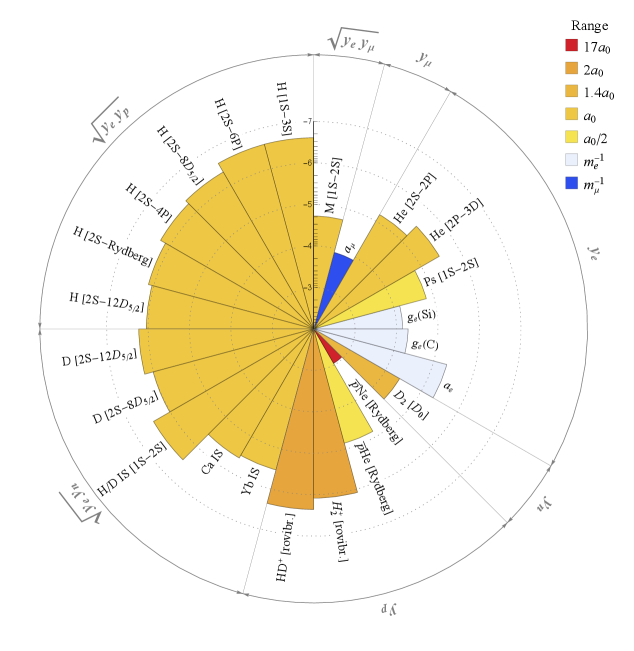
В статье представлен обзор современных спектроскопических методов, позволяющих искать проявления физики за пределами общепринятой Стандартной модели.
![Сферические косы, подобные обычным косам Артина, описывают траектории точек на сфере, однако, в отличие от последних, коса, образованная последовательностью элементов [latex]b_1 \cdot s b_n[/latex] и обратной последовательностью [latex]b_n \cdot s b_1[/latex] при фиксированных точках, кроме одной обходящей остальные, топологически тривиальна.](https://arxiv.org/html/2602.18748v1/graphics/SphericalBraid-labeled.png)
В статье представлена теоретическая модель, описывающая возникновение неабелевых аньонов в жидкостях дробного квантового эффекта Холла, индуцированных сверхпроводящими островами.