Квантовая запутанность на заре столкновений частиц
Новое исследование показывает, как поляризация пучков электронов и позитронов влияет на квантовую запутанность и нелокальность гиперон-антигиперонных пар.
Наука
Квантовые узоры: Как неупорядоченность меняет поведение неэрмитовых систем
![В данной модели изучается влияние асимметричного скачка [latex]J e^{\pm\alpha}[/latex], квазипериодического потенциала на месте [latex]\lambda_j[/latex] и настраиваемой силы скачка примеси μ на поведение системы, демонстрируя возможность тонкой настройки её характеристик за счёт управления этими параметрами.](https://arxiv.org/html/2602.11155v1/x1.png)
Новое исследование показывает, что введение квазипериодичности в неэрмитовые системы может приводить к переходу от локализованных состояний к эффекту неэрмитовой кожи или расширенным состояниям.
Квантовые грани вакуума: новый предел точности
Исследователи приблизились к фундаментальному пределу чувствительности при измерении нелинейных оптических эффектов в пустом пространстве, открывая путь к более глубокому пониманию квантовой электродинамики.
Квантовая запутанность гиперонов: эволюция и перераспределение
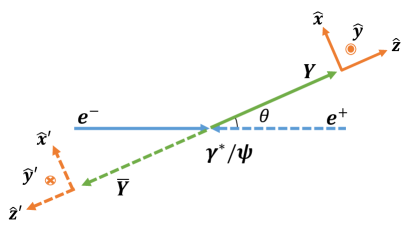
![Определение углов гелицитности для распадов [latex]e^{+}e^{-}\to Y\bar{Y}[/latex] и последовательного распада [latex]Y\rightarrow\Lambda\pi[/latex] позволяет установить взаимосвязь между спиновыми состояниями частиц и кинематическими параметрами процесса, при этом аналогичные определения для [latex]\bar{Y}\rightarrow\bar{\Lambda}\pi[/latex] опущены для краткости.](https://arxiv.org/html/2602.10398v1/diagram_new.png)
Новое исследование показывает, как квантовая запутанность изменяется в процессе распада пар гиперон-антигиперон, открывая возможности для управления квантовыми корреляциями.
Асимметрия взаимодействий: Новая физика многочастичных систем
В этом обзоре рассматриваются проявления и последствия нарушения симметрии взаимодействий в сложных квантовых системах, открывающие путь к новым фазам материи и необычным динамическим режимам.
Волны материи в танце: управление взаимодействиями в конденсатах Бозе-Эйнштейна
![В ходе экспериментов по четырехволновому смешению (FWM) одиночных и двухкомпонентных спинов, последовательное применение брагговских импульсов позволило сгенерировать различные состояния импульса, при этом для двухкомпонентных спинов, взаимодействие с лазерным полем на длине волны 769.35 нм выявило два рассеянных состояния импульса для спина «вниз» при [latex]\lvert\pm 2\hbar k\rangle[/latex], демонстрируя симметричные FWM-процессы, визуализированные в виде волновых пакетов.](https://arxiv.org/html/2602.10873v1/x1.png)
Новое исследование демонстрирует возможности точного управления четырехволновым смешением (ЧВС) в конденсатах Бозе-Эйнштейна из изотопа калия-39, открывая перспективы для квантовых технологий.
Тень материи: как окружение влияет на вращающиеся черные дыры
![Радиальный профиль угловой скорости увлечения, вызванного вращающимся телом в пространстве-времени, окружённом гало из тёмной материи, демонстрирует отклонение от поведения в вакууме, обусловленное влиянием гало, моделируемого как анизотропное вещество с плотностью по типу Эрнквиста, причём конфигурация гало, определяемая параметрами [latex]Loga\_0[/latex] и [latex]LogM\_{\rm Halo}[/latex], оказывает заметное воздействие на инерционное увлечение.](https://arxiv.org/html/2602.10579v1/x2.png)
Новое исследование показывает, как темная материя, окружающая черную дыру, искажает пространство-время вокруг нее, изменяя траектории орбит и сигналы гравитационных волн.
Топ-кварк как ключ к новой физике
Новое исследование всесторонне анализирует взаимодействия топ-кварка, нарушающие сохранение аромата, в рамках эффективной теории поля, открывая путь к поиску отклонений от Стандартной модели.
Квантовая Вселенная: Новая модель без сингулярности
Исследование применяет модифицированную теорию гравитации f(R,T) и квантовую космологию для поиска решений проблемы сингулярности в ранней Вселенной.
Пыль и гравитация: сможет ли Вселенная отскочить?
![В исследовании демонстрируется, что при заданном минимальном радиусе [latex]L_0 = 0.2L[/latex] и массе [latex]M = 1[/latex], плотность и масса пыли внутри внешней границы зависят от радиальной координаты, отражая закономерности распределения материи в подобных системах.](https://arxiv.org/html/2602.10804v1/x2.png)
Новое исследование показывает, что коллапс пылевидной материи в сферически симметричном пространстве-времени может избежать сингулярности и привести к отскоку без дополнительных предположений.