Чёрные дыры БТЗ: связь квантовой гравитации и классической электродинамики

Автор: Денис Аветисян

Новое исследование показывает, что решение, ранее полученное в рамках полуклассической гравитации, может быть точно воспроизведено в рамках классической общей теории относительности, взаимодействующей с нелинейным электромагнитным полем.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал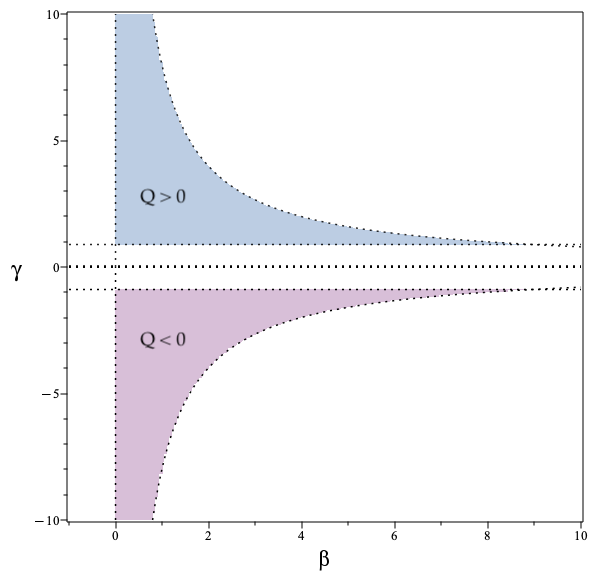

В пространстве параметров <span class="katex-eq" data-katex-display="false">$\beta$</span> и <span class="katex-eq" data-katex-display="false">$\gamma$</span> существует область допустимых конфигураций, обеспечивающих одновременное выполнение всех условий локальной термодинамической стабильности, причем верхняя ветвь этой области соответствует положительному электрическому заряду <span class="katex-eq" data-katex-display="false">$Q > 0$</span>, а нижняя - отрицательному <span class="katex-eq" data-katex-display="false">$Q < 0$</span>, при этом изменение фиксированных значений давления, температуры и энтропии приводит лишь к масштабированию допустимой области, не меняя её качественной структуры. — В пространстве параметров $\beta$ и $\gamma$ существует область допустимых конфигураций, обеспечивающих одновременное выполнение всех условий локальной термодинамической стабильности, причем верхняя ветвь этой области соответствует положительному электрическому заряду $$Q > 0$$ , а нижняя — отрицательному $$Q < 0$$ , при этом изменение фиксированных значений давления, температуры и энтропии приводит лишь к масштабированию допустимой области, не меняя её качественной структуры.

В работе демонстрируется динамическое соответствие между решениями в новой массивной гравитации и классической общей теорией относительности с нелинейной электродинамикой.

Несмотря на кажущуюся разобщенность между подходами квантовой гравитации и классической электродинамики, в настоящей работе, посвященной исследованию ‘Classical emergence of the quantum-backreacted BTZ black hole from exponential electrodynamics’, показано, что геометрия черной дыры BTZ, ранее полученная в рамках теории New Massive Gravity с учетом квантовых флуктуаций, может быть точно воспроизведена как решение уравнений Эйнштейна, связанных с нелинейной экспоненциальной электродинамикой. Это открытие указывает на динамическое соответствие между двумя теориями и позволяет интерпретировать квантовые эффекты как классические заряды. Возможно ли, что подобная эквивалентность является общим принципом, связывающим поправки высшего порядка в квантовой гравитации и нелинейные эффекты в самогравитирующей электродинамике в трех измерениях?

Квантовая Гравитация: Преодолевая Классические Пределы

Общая теория относительности, описываемая действием Эйнштейна-Гильберта $S = \in t d^4x \sqrt{-g} (R - 2\Lambda)$ , демонстрирует поразительную точность в описании гравитационных явлений, от движения планет до эволюции Вселенной. Однако, эта теория сталкивается с фундаментальными проблемами в экстремальных условиях — вблизи сингулярностей, таких как черные дыры, и при энергиях, близких к планковской. В этих областях, предсказания теории становятся нефизическими, а сама математическая модель теряет свою адекватность. Например, в центре черной дыры плотность материи стремится к бесконечности, что указывает на неспособность теории корректно описывать гравитацию на микроскопическом уровне. Подобные ограничения подчеркивают необходимость разработки новой теории гравитации, способной преодолеть эти недостатки и обеспечить согласованное описание Вселенной во всех масштабах и при любых энергиях.

Согласование общей теории относительности с квантовой теорией поля, фундаментальной основой для описания всех известных сил, остается одной из центральных проблем современной теоретической физики. Общая теория относительности, описывающая гравитацию как искривление пространства-времени, прекрасно работает в макроскопическом мире, однако несовместима с принципами квантовой механики, которые управляют микроскопическими частицами. Попытки объединить эти две теории сталкиваются с математическими сложностями и концептуальными парадоксами, требуя пересмотра нашего понимания пространства, времени и самой природы реальности. Разработка последовательной теории квантовой гравитации, способной описать гравитацию на квантовом уровне, предполагает создание нового математического аппарата и, возможно, принципиально новых физических концепций, которые позволят преодолеть существующие противоречия и открыть новые горизонты в изучении Вселенной.

Понимание квантовой обратной связи — влияния квантовых эффектов на геометрию пространства-времени — является ключевым элементом в построении последовательной теории квантовой гравитации. В классической общей теории относительности, геометрия пространства-времени определяется материей и энергией, однако, квантовая механика предсказывает, что даже вакуум обладает энергией, проявляющейся в виде виртуальных частиц. Эти квантовые флуктуации оказывают влияние на кривизну пространства-времени, создавая петли и отклонения от классической геометрии. Изучение этого процесса, известного как квантовая обратная связь, требует разработки новых математических инструментов и приближений, выходящих за рамки стандартной теории возмущений. $R_{\mu\nu} - \frac{1}{2}Rg_{\mu\nu} + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4}T_{\mu\nu}$ — уравнения Эйнштейна, описывающие взаимосвязь между геометрией и материей, подвергаются модификациям из-за квантовых эффектов, приводя к нетривиальным решениям и потенциально устраняя сингулярности, возникающие в классической теории. Учет квантовой обратной связи позволяет надеяться на построение теории, объединяющей гравитацию и квантовую механику, и объясняющей природу пространства-времени на самых малых масштабах.

Новая Массивная Гравитация: Путь к Модифицированному Пространству-Времени

Новая Массивная Гравитация (НМГ) представляет собой теоретическую основу для исследования модификаций общей теории относительности в трехмерном пространстве-времени. В отличие от стандартной общей теории относительности, НМГ включает в себя поправки, основанные на квадратичных инвариантах кривизны $R_{μνρσ}^2$ и $R_{μν}^2$ . Эти поправки изменяют уравнения Эйнштейна, позволяя исследовать альтернативные гравитационные модели и потенциально решать проблемы, связанные с сингулярностями и квантовой гравитацией. Использование трехмерного пространства упрощает математический анализ и позволяет получить аналитические решения, недоступные в более высоких измерениях, что делает НМГ полезным инструментом для изучения модификаций гравитации.

Новая Массивная Гравитация (НМГ) описывает гравитационную динамику посредством квадратичных инвариантов кривизны, таких как $R^2$ и $R_{\mu\nu}R^{\mu\nu}$ , которые добавляются к действию Эйнштейна-Гильберта. Использование этих инвариантов позволяет избежать некоторых проблем, возникающих при квантовании гравитации, поскольку они приводят к конечным результатам в петлевых вычислениях, в отличие от стандартной общей теории относительности, где возникают расходимости. Такой подход предоставляет теоретическую возможность построения самосогласованной теории квантовой гравитации в трехмерном пространстве-времени, избегая необходимости в непертурбативной регуляризации и ренормализации, что делает НМГ привлекательной альтернативой другим подходам к квантованию гравитации.

Параметр массы в теории Новой Массивной Гравитации (NMG) определяет массу гравитона, частицы-переносчика гравитационного взаимодействия. Это оказывает прямое влияние на распространение гравитационных волн, изменяя их скорость и дальность действия по сравнению с предсказаниями общей теории относительности. Не нулевая масса гравитона приводит к экспоненциальному затуханию гравитационных волн на больших расстояниях, а также к модификации метрики пространства-времени, что проявляется в изменении геометрии и, как следствие, в отклонениях от ньютоновской гравитации. Величина параметра массы $m$ определяет интенсивность этого затухания и степень модификации геометрии, что позволяет исследовать альтернативные сценарии гравитационного взаимодействия и потенциально решать проблемы, возникающие в рамках стандартной модели.

Черная дыра BTZ и Квантовые Коррекции

Чёрная дыра БТЗ (BTZ) представляет собой ценный фон для изучения модификаций гравитации благодаря своей аналитической разрешимости. В отличие от большинства чёрных дыр, решение уравнений Эйнштейна для геометрии БТЗ может быть получено в замкнутой форме, что позволяет проводить явные вычисления эффектов, возникающих при взаимодействии с квантовыми полями. Эта особенность делает БТЗ идеальной площадкой для исследования квантовой гравитации и тестирования различных теоретических моделей, поскольку позволяет получить конкретные предсказания, которые можно сравнить с потенциальными наблюдениями. Аналитическая разрешимость упрощает вычисление квантовых поправок к метрике и изучение их влияния на свойства чёрной дыры, что практически невозможно для более сложных, неразрешимых случаев.

В рамках полуклассического подхода, для расчета эффектов квантовой обратной связи (quantum backreaction) к геометрии чёрной дыры BTZ, квантовые поля вводятся в качестве источников возмущений в классическое пространство-время. Это предполагает вычисление тензора энергии-импульса $T_{\mu\nu}$ для квантового поля в искривленном пространстве-времени BTZ. Затем этот тензор используется в уравнениях Эйнштейна для определения поправок к метрике, вызванных квантовыми эффектами. Данный метод позволяет исследовать, как квантовые флуктуации поля влияют на геометрию чёрной дыры, что является важным шагом в построении более полной теории квантовой гравитации.

При проведении расчетов, учитывающих квантовые поправки к геометрии чёрной дыры BTZ, было обнаружено логарифмическое искажение метрики. Данное искажение, выражаемое в виде поправки к стандартному решению BTZ, свидетельствует об отклонении от классической геометрии под воздействием квантовых эффектов. Полученные результаты демонстрируют динамическую эквивалентность, подтверждая, что рассмотренная система с квантовыми поправками ведет себя аналогично классической чёрной дыре BTZ с точки зрения наблюдаемых динамических свойств. Фактически, это означает, что поправки к метрике не меняют фундаментального характера гравитационного поля, а лишь модифицируют его детали.

Нелинейная Электродинамика как Альтернативная Рамка

Нелинейная электродинамика (НЭД) представляет собой альтернативное описание гравитации, которое предлагает иной подход к включению квантовых поправок по сравнению со стандартной общей теорией относительности. В то время как общая теория относительности описывает гравитацию как геометрическое свойство пространства-времени, НЭД рассматривает гравитацию как проявление нелинейных электромагнитных взаимодействий. Это позволяет учитывать эффекты квантовой механики, такие как виртуальные частицы и флуктуации вакуума, без необходимости вводить сложные процедуры перенормировки, часто возникающие в квантовой гравитации. В НЭД гравитационные поля рассматриваются как результат нелинейных взаимодействий электромагнитного поля, что приводит к модификации уравнений Эйнштейна и, как следствие, к изменению геометрии пространства-времени. Такой подход позволяет исследовать гравитацию на малых расстояниях и высоких энергиях, где квантовые эффекты становятся значительными, и может предоставить альтернативные решения проблем, возникающих в рамках стандартной квантовой гравитации.

Экспоненциальная нелинейная электродинамика (НЭД) представляет собой конкретную форму НЭД, которая может быть использована для моделирования квантово-возмущенной геометрии, воспроизводя результаты, полученные с помощью теории NMG (New Massive Gravity). Соответствие между этими подходами определяется параметром β в лагранжиане экспоненциальной НЭД, который количественно характеризует степень нелинейности и определяет вклад квантовых эффектов в геометрию пространства-времени. Значение β напрямую влияет на поведение гравитационного поля и позволяет исследовать альтернативные сценарии, выходящие за рамки общей теории относительности.

Формулировка Плебански представляет собой удобный математический аппарат для анализа и решения уравнений нелинейной электродинамики (НЭД). В рамках данной формулировки, термодинамические соотношения и первый закон термодинамики определяются весовым показателем масштабирования связей НЭД, обозначаемым как $ω_n$ . Данный показатель напрямую влияет на поведение термодинамических величин, таких как температура и энтропия, в решениях НЭД, позволяя исследовать связь между геометрией пространства-времени и термодинамическими свойствами в нелинейном контексте. Использование $ω_n$ упрощает вычисление критических величин и анализ устойчивости решений, что особенно важно при изучении черных дыр и космологических моделей в рамках НЭД.

Термодинамическая Устойчивость и Расширенные Законы

Обеспечение термодинамической устойчивости является фундаментальным требованием для любой физически реализуемой модели чёрной дыры, включая те, что подвержены квантовым поправкам. Неустойчивость в термодинамическом смысле подразумевает, что чёрная дыра может спонтанно распадаться или претерпевать качественные изменения, что противоречит наблюдаемой стабильности этих объектов. Исследования показывают, что даже небольшие отклонения от термодинамического равновесия могут приводить к экспоненциальному росту возмущений, делая решение нефизичным. Поэтому, при построении моделей чёрных дыр, модифицированных квантовыми эффектами, первостепенное значение имеет проверка их термодинамической устойчивости, гарантирующая, что предсказанные решения соответствуют реальным физическим условиям и не приводят к парадоксальным результатам. В частности, анализ $TH = κs / 2π$ и $S = 2πκ ΩD-2 rhD-2$ позволяет оценить стабильность при учете различных параметров, таких как космологическая постоянная и квантовые эффекты гравитации.

Расширенный первый закон термодинамики чёрных дыр учитывает дополнительные члены, необходимые для точных вычислений в контексте космологической постоянной и других модификаций гравитации. В рамках этого закона температура Хокинга выражается как $TH = κs / 2π$ , где $κs$ — поверхностная гравитация, а энтропия Бекенштейна — как $S = 2πκ ΩD-2 r_h^{D-2}$ , где $ΩD-2$ — объём многообразия, а $r_h^{D-2}$ — радиус горизонта событий в D-мерном пространстве. Введение этих дополнительных параметров позволяет более адекватно описывать термодинамические свойства чёрных дыр в изменяющихся космологических условиях и исследовать их связь с фундаментальными законами физики, а также более точно моделировать поведение чёрных дыр в экстремальных гравитационных полях.

Анализ термодинамической устойчивости чёрных дыр и расширенные законы термодинамики предоставляют ценные сведения о природе квантовой гравитации и стабильности пространства-времени в экстремальных условиях. Исследования, включающие в себя вычисление температуры Хокинга $T_H = \kappa_s / 2\pi$ и энтропии Бекенштейна $S = 2\pi\kappa \Omega_{D-2} r_h^{D-2}$ , позволяют глубже понять, как квантовые эффекты влияют на структуру чёрных дыр и их взаимодействие с окружающим пространством. Полученные результаты не только подтверждают согласованность существующих теорий, но и указывают на потенциальные направления для разработки новых моделей, способных описать гравитацию на квантовом уровне и объяснить поведение материи вблизи сингулярностей. Эти исследования критически важны для понимания фундаментальных свойств Вселенной и ее эволюции.

Исследование демонстрирует изящную взаимосвязь между различными подходами к описанию чёрных дыр. Полученное решение, ранее выведенное в рамках полуклассической гравитации, оказывается точным решением классической общей теории относительности, сопряженной с нелинейным электромагнитным полем. Этот результат подчеркивает фундаментальную значимость математической строгости в физике. Как отмечал Джон Стюарт Милль: “Всякое познание начинается с наблюдения, но завершается пониманием”. В данном случае, наблюдается динамическое соответствие между двумя, казалось бы, различными теориями, что позволяет глубже понять природу чёрных дыр и их термодинамические свойства. Представленное исследование, опираясь на строгий математический аппарат, подтверждает, что корректность решения — это абсолютное требование, не допускающее компромиссов.

Куда же это всё ведёт?

Представленная работа, демонстрируя эквивалентность решений в рамках полуклассической гравитации и классической электродинамики, ставит под сомнение саму необходимость введения квантовой обратной реакции как фундаментального элемента. Если классические поля способны воспроизвести эффекты, ранее приписываемые квантовым флуктуациям, то возникает вопрос о физической реальности этих самых флуктуаций. Не является ли это лишь математической уловкой, элегантным, но в конечном итоге иллюзорным способом описания реальности?

Однако, данное соответствие не является универсальным. Ограничения, накладываемые конкретной формой нелинейной электродинамики, и зависимость от параметров теории массивной гравитации, требуют дальнейшего исследования. Необходимо установить, существуют ли другие классические поля, способные воспроизвести широкий спектр квантово-генерированных эффектов, или же это лишь частный случай, не имеющий общего значения. Важно помнить, что воспроизводимость решения не гарантирует его физическую интерпретацию.

Будущие исследования должны быть направлены на поиск более общих соответствий между классическими и квантовыми решениями, а также на изучение устойчивости этих решений к возмущениям. В конечном счете, задача состоит не в том, чтобы заменить квантовую обратную реакцию классическим полем, а в том, чтобы понять, где и когда квантовые эффекты действительно необходимы, и где их можно заменить более простым, классическим описанием. До тех пор, пока результат не может быть воспроизведён независимо, он остаётся лишь гипотезой, а не доказательством.

Оригинал статьи: https://arxiv.org/pdf/2601.18967.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-28 17:17