Дальний порядок из ничего: связь импульса и запутанности в одномерных системах

Автор: Денис Аветисян

---

Новое исследование демонстрирует неожиданную связь между импульсом частиц и дальнодействующей квантовой запутанностью в системах с нарушенной трансляционной симметрией.

Ожидаемое значение оператора трансляции определяет длину локализации и характеризует дальнодействующую запутанность в одномерных системах с нарушенной трансляционной симметрией.

Несмотря на то, что в системах с сохранением симметрии переноса связь между ненулевым импульсом и дальнодействующим запутанным состоянием установлена, вопрос о возможности прямого кодирования характера запутанности в состояниях без такой симметрии остается открытым. В настоящей работе, опираясь на результаты, представленные в статье ‘Non-zero Momentum Implies Long-Range Entanglement When Translation Symmetry is Broken in 1D’, мы показываем, что для одномерных систем величина среднего значения оператора переноса <t> в пределе непрерывного спектра обязательно стремится к единице для делокализованных состояний, что служит индикатором дальнодействующего запутанного состояния. Какие новые подходы позволит разработать использование распределения импульса для характеристики запутанности в многомерных системах и системах с топологическим порядком?

---

Импульс и Основы Квантовых Состояний

Понимание распределения импульса квантового состояния является ключевым для характеристики его поведения, что определяется фундаментальным принципом неопределенности. Данное распределение, представляющее собой вероятность обнаружения частицы с определенным импульсом, тесно связано с пространственным распределением вероятности её нахождения. \Delta x \Delta p \geq \hbar/2 — данное неравенство, являющееся следствием волновой природы материи, указывает на то, что чем точнее определено положение частицы, тем менее точно можно определить её импульс, и наоборот. Таким образом, анализ распределения импульса позволяет сделать вывод о степени локализации частицы и её способности к распространению в пространстве, предоставляя ценную информацию о динамических свойствах квантовой системы и её потенциальном взаимодействии с другими системами.

Распределение импульса, определяющее поведение одночастичных собственных состояний, предоставляет ключевую информацию о локализации и распространении частицы в квантовом мире. Именно анализ этого распределения позволяет понять, насколько определенно можно установить положение частицы, и как сильно она «размазана» в пространстве. Чем более узким является распределение импульса, тем более локализована частица, и наоборот — широкое распределение свидетельствует о большей неопределенности в определении её положения. Этот взаимосвязанный характер локализации и распространения, напрямую вытекающий из принципа неопределенности Гейзенберга \Delta x \Delta p \ge \frac{\hbar}{2}, является фундаментальным свойством квантовых систем и оказывает определяющее влияние на их поведение и свойства.

Симметрия переноса играет фундаментальную роль в определении распределения импульса квантового состояния. Вследствие этой симметрии, импульс является сохраняющейся величиной, что напрямую влияет на допустимые состояния частицы и их соответствующие волновые функции. В частности, теорема Нётер устанавливает прямую связь между симметрией переноса и сохранением импульса, что приводит к тому, что собственные состояния оператора импульса образуют полный базис. Это означает, что любое квантовое состояние может быть представлено как суперпозиция состояний с определенным импульсом. Следовательно, знание о симметрии переноса позволяет установить ограничения на возможные формы волновых функций и предсказать поведение частиц в различных потенциалах, определяя, какие импульсы разрешены, а какие — нет, и, таким образом, формируя характер распределения импульса \hat{p}.

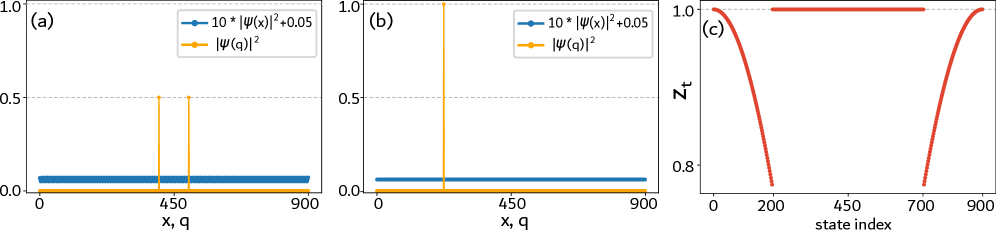
Квантование Локализации: Введение Длины Локализации

Длина локализации является точной мерой степени пространственной ограниченности квантового состояния, предоставляя информацию о его пространственном размахе. В отличие от простого определения радиуса или ширины волновой функции, длина локализации учитывает вероятностное распределение частицы в пространстве и количественно определяет, насколько «сжато» состояние вокруг определенной точки. Математически, она определяется как \sqrt{\langle x^2 \rangle - \langle x \rangle^2} , где \langle x \rangle — среднее значение координаты, а \langle x^2 \rangle — среднее значение квадрата координаты. Меньшее значение длины локализации указывает на более сильную локализацию состояния, в то время как большое значение свидетельствует о его размытости и распределенности в пространстве. Этот параметр особенно важен при изучении систем с ограниченными размерами, таких как квантовые точки или дефекты в кристаллах.

Длина локализации напрямую связана с распределением по импульсам, отражая обратную зависимость между пространственной локализацией и разбросом импульсов. Математически, более узкое распределение в координатном пространстве соответствует более широкому распределению в импульсном пространстве и наоборот. \Delta x \Delta p \geq \frac{\hbar}{2} — данное соотношение неопределенностей демонстрирует фундаментальную связь. При приближении длины локализации к нулю состояние становится сильно локализованным, что соответствует широкому распределению по импульсам. И наоборот, бесконечное значение длины локализации указывает на полностью делокализованное состояние, характеризующееся узким распределением по импульсам.

Для обеспечения корректности определения длины локализации и ее применимости к макроскопическим системам необходимо рассмотрение пределов непрерывности и термодинамического предела. Предел непрерывности, подразумевающий бесконечное увеличение размера системы, позволяет исключить влияние граничных условий и приблизить поведение к континуальному. Термодинамический предел, соответствующий бесконечному увеличению числа частиц, обеспечивает статистическую достоверность измеряемых величин и позволяет корректно описывать коллективные эффекты. В этих пределах, L (длина локализации) становится осмысленной физической характеристикой, отражающей степень пространственной локализации квантового состояния в исследуемой системе, и ее значение может быть сопоставлено с макроскопическими параметрами системы.

Теоретические Инструменты: Операторы и Формула Реста

Оператор переноса представляет собой мощный математический инструмент для анализа импульсных характеристик квантовых состояний. В квантовой механике, оператор переноса \hat{T}(p) действует на волновую функцию \psi(x), сдвигая её в импульсном пространстве. Анализ собственных значений и собственных функций этого оператора позволяет определить распределение вероятностей нахождения частицы с определенным импульсом. Использование оператора переноса позволяет переходить от пространственного представления волновой функции к импульсному, что необходимо для вычисления различных физических величин, связанных с импульсом, таких как среднее значение импульса и дисперсия.

Оператор трансляции, в сочетании с его математическим ожиданием, позволяет напрямую связать свойства оператора с распределением импульса. Величина математического ожидания оператора трансляции \langle T \rangle характеризует степень пространственной локализации волновой функции. Значения, приближающиеся к 1, указывают на делокализованное состояние, то есть, вероятность обнаружения частицы равномерно распределена в пространстве, а локализация отсутствует. Следовательно, анализ математического ожидания оператора трансляции предоставляет количественную оценку степени делокализации квантового состояния и является инструментом для изучения импульсных свойств.

Формула Реста устанавливает связь между длиной локализации и модулярным оператором положения, что позволяет количественно оценить степень локализации квантового состояния. В частности, установлено, что существует корреляция между величиной математического ожидания оператора трансляции \langle T \rangle и длиной локализации. Более высокая величина \langle T \rangle указывает на большую степень делокализации состояния, поскольку оператор трансляции описывает изменение импульса, а его математическое ожидание связано с пространственным распределением вероятности. Таким образом, формула Реста предоставляет инструмент для анализа степени локализации квантовых состояний на основе характеристик оператора трансляции.

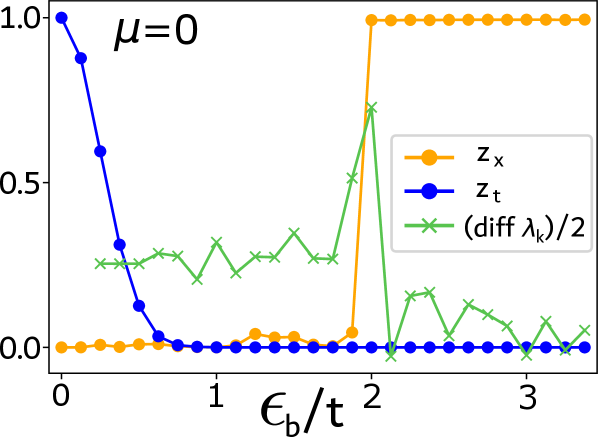
Иллюстративные Модели: Детерминированный Димер и За Его Пределами

Детерминированная модель димера выступает в роли ценного полигона для исследования взаимосвязи между локализацией и импульсом в квантовых системах. Данная модель, благодаря своей простоте и управляемости, позволяет исследователям точно контролировать степень локализации волновой функции и наблюдать, как это влияет на распределение импульсов. Изучение этой взаимосвязи особенно важно, поскольку позволяет проверить теоретические предсказания о поведении волновых пакетов и углубить интуитивное понимание квантовомеханических явлений, таких как туннелирование и интерференция. Использование модели димера позволяет отделить фундаментальные эффекты локализации от более сложных взаимодействий, что делает её незаменимым инструментом в области квантовой физики конденсированного состояния.

Анализ распределения импульса в детерминированной модели димера предоставляет ценную возможность проверки теоретических предсказаний и формирования интуитивного понимания поведения квантовых систем. Изучение формы этой функции позволяет сопоставить результаты моделирования с аналитическими решениями, подтверждая или опровергая справедливость используемых приближений и методов расчета. Более того, детальное рассмотрение особенностей распределения импульса, таких как его ширина и наличие пиков, способствует более глубокому пониманию взаимосвязи между пространственным распределением вероятности и энергией частицы. Это, в свою очередь, позволяет предсказывать и интерпретировать поведение системы в различных условиях, а также использовать модель димера в качестве отправной точки для изучения более сложных квантовых явлений и систем.

Исследование влияния введения магнитного потока на распределение по импульсам демонстрирует фундаментальные аспекты взаимодействия квантовых состояний с внешними воздействиями. Установлено, что фаза математического ожидания оператора трансляции, характеризующего смещение частицы, существенно изменяется при введении потока для делокализованных состояний, что указывает на их чувствительность к внешним магнитным полям. В то же время, для локализованных состояний эта фаза остается неизменной, свидетельствуя об их устойчивости к подобным возмущениям. Данный результат позволяет глубже понять природу локализации и делокализации в квантовых системах, а также использовать манипуляции с магнитным потоком для контроля и управления квантовыми состояниями. \langle \hat{T} \rangle — математическое ожидание оператора трансляции.

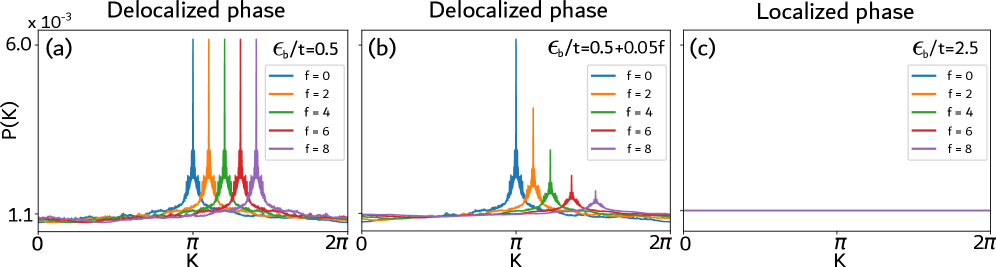
Запутанность и Природа Квантовых Корреляций

Длина локализации играет ключевую роль в определении дальности квантовой запутанности, что позволяет разграничить запутанность короткого и дальнего радиуса действия. Этот параметр, характеризующий степень пространственного ограничения волновой функции, непосредственно влияет на то, насколько далеко могут сохранять корреляцию две или более квантовые частицы. В материалах с большой длиной локализации, волновые функции распространяются на значительные расстояния, способствуя возникновению запутанности на макроскопическом уровне. Напротив, в системах с короткой длиной локализации, запутанность ограничивается небольшим пространственным регионом. Понимание этой взаимосвязи имеет решающее значение для разработки квантовых технологий, где поддержание запутанности на больших расстояниях является необходимым условием для эффективной передачи и обработки квантовой информации. Исследования в этой области позволяют создавать материалы с заданными свойствами, оптимизированными для конкретных приложений в квантовых вычислениях и коммуникациях.

Понимание взаимосвязи между длиной локализации и дальнодействующим запутанным состоянием имеет решающее значение для развития квантовых технологий. Сохранение запутанности на больших расстояниях — необходимое условие для создания эффективных квантовых сетей, безопасной квантовой связи и мощных квантовых вычислений. В частности, способность контролировать и увеличивать длину локализации позволяет создавать системы, в которых квантовые корреляции сохраняются на масштабах, необходимых для практического применения. Разработка материалов и архитектур, оптимизированных для поддержания запутанности на больших расстояниях, открывает перспективы для создания принципиально новых квантовых устройств, превосходящих возможности классических технологий в решении сложных задач.

Дальнейшее изучение взаимосвязи между длиной локализации и дальнодействующим запутанным состоянием открывает перспективы для углубленного понимания фундаментальных строительных блоков квантовой материи. Исследования в этой области не только проясняют природу квантовых корреляций, но и создают основу для разработки принципиально новых квантовых устройств. В частности, контроль над длиной локализации позволит создавать материалы с предсказуемыми свойствами запутанности, что необходимо для реализации надежных квантовых вычислений и коммуникаций. Ожидается, что эти достижения приведут к появлению более эффективных квантовых сенсоров, способных к сверхчувствительным измерениям, и откроют новые возможности в области квантовой криптографии, обеспечивая беспрецедентный уровень безопасности передачи информации.

Исследование демонстрирует, что нарушение симметрии переноса влечёт за собой дальнодействующую запутанность, что напрямую связано с ожидаемым значением оператора переноса. Это поднимает важный вопрос об ответственности за автоматизированные системы. Как и утверждал Иммануэль Кант: «Действуй так, чтобы максима твоей воли могла в то же время стать всеобщим законом природы». В данном контексте, каждый алгоритм, кодирующий отсутствие учета уязвимых состояний, несёт долг перед обществом. Понимание связи между моментом и длиной локализации — это не просто математическая задача, но и этический императив: прогресс без этики — это ускорение без направления.

Куда двигаться дальше?

Представленная работа, демонстрируя связь между ожидаемым значением оператора трансляции и локализационными свойствами систем без трансляционной симметрии, открывает новые возможности для характеристики запутанности. Однако, следует признать, что подобный формализм, хоть и элегантен, пока что оперирует с абстрактными математическими конструкциями. Вопрос о том, насколько адекватно эти теоретические выводы отражают физическую реальность в конкретных, сложных системах, остаётся открытым. Необходимо разработать методы, позволяющие применять этот подход к анализу реальных материалов и устройств.

Важно понимать, что данные сами по себе нейтральны, но модели отражают предвзятости людей. Поэтому, при создании алгоритмов для анализа запутанности, необходимо учитывать потенциальные источники систематических ошибок и предубеждений. Иначе, инструмент, призванный раскрывать фундаментальные свойства материи, может стать орудием для подтверждения заранее заданных теорий. Прогресс без этики — это ускорение без направления.

Будущие исследования, вероятно, будут направлены на расширение данного формализма для рассмотрения систем с более сложной топологией и взаимодействиями. Интересным направлением представляется изучение возможности использования этого подхода для разработки новых методов контроля и манипулирования квантовой запутанностью. Инструменты без ценностей — это оружие, и их создание требует особой ответственности.

---

Оригинал статьи: https://arxiv.org/pdf/2601.15345.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

• Все рецепты культистского круга в Escape from Tarkov

• Решение головоломки с паролем Absolum в Yeldrim.

• Лучшие транспортные средства в Far Cry 6

• Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip

• Лучшие шаблоны дивизий в Hearts Of Iron 4

• Как получить скины Alloyed Collective в Risk of Rain 2

• The Planet Crafter: расположение ключей Стража

• В стороне: QB и я В ролях: каждый актер, который появляется (фотографии)

• 15 лучших законченных серий манхвы, которые стоит прочитать, в рейтинге

• Где найти и поймать бабочку Солнечного луча в Палии

2026-01-23 17:33