Энтропия пространства-времени: новый взгляд на квантовую запутанность

Автор: Денис Аветисян

---

Исследование предлагает новый подход к определению энтропии пространства-времени для квантовых полей, применимый даже в дискретных моделях, таких как причинные множества.

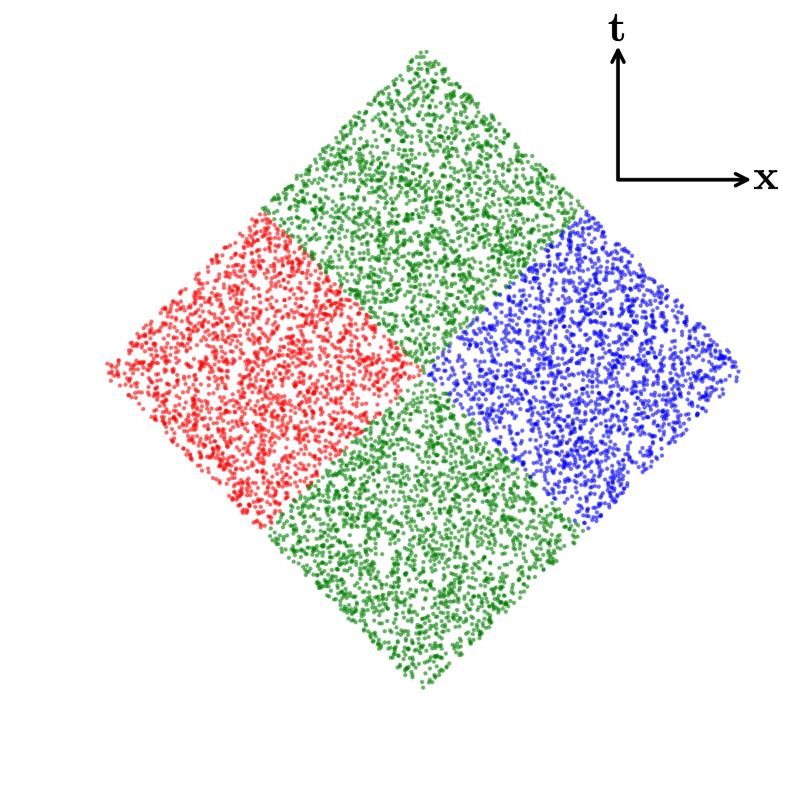
Разработана ковариантная и спектрально определенная формулировка энтропии пространства-времени для квазисвободных теорий.

Традиционные подходы к вычислению энтропии запутанности сталкиваются с трудностями при ультрафиолетовой регуляризации. В работе ‘Spectral Spacetime Entropy for Quasifree Theories’ предложен новый спектральный метод расчета энтропии для квазисвободных полей, применимый как к бозонным, так и к фермионным теориям. Данное построение, определяемое в пространстве-времени, а не на гиперповерхности, обеспечивает ковариантную регуляризацию энтропий и может быть использовано в произвольных областях пространства-времени, что особенно актуально для полуклассической и квантовой гравитации. Может ли предложенный подход выявить признаки дискретности пространства-времени, например, в рамках теории причинных множеств?

---

Пространство-Время: Классическая Картина Мира

Квантовая теория поля опирается на понятие пространственно-временного многообразия для описания Вселенной, рассматривая его как основу, на которой разворачиваются все физические процессы. Однако, при рассмотрении экстремальных гравитационных сценариев, таких как черные дыры или Большой взрыв, данная структура сталкивается с серьезными трудностями. В этих условиях, геометрия пространства-времени становится настолько искаженной, что привычные математические инструменты, используемые для описания квантовых полей, перестают работать корректно. Возникают сингулярности и бесконечности, что указывает на необходимость разработки новых теоретических подходов, способных преодолеть ограничения классического представления о пространстве-времени и обеспечить адекватное описание физической реальности в самых экстремальных условиях. По сути, это означает, что сама концепция гладкого и непрерывного многообразия может оказаться недостаточной для описания Вселенной на самых фундаментальных уровнях.

Пространство Гильберта представляет собой фундаментальную математическую структуру, в которой описываются все возможные квантовые состояния, и эта структура неразрывно связана с геометрией пространства-времени, используемой в квантовой теории поля. Фактически, каждая точка в пространстве Гильберта соответствует определенному квантовому состоянию, а взаимосвязи между этими точками определяются метрикой пространства-времени. Именно эта связь позволяет описывать физические процессы, такие как взаимодействие частиц, как эволюцию во времени квантовых состояний в этом математическом пространстве. Понимание этой взаимосвязи критически важно, поскольку изменения в геометрии пространства-времени, вызванные, например, гравитацией, напрямую влияют на структуру пространства Гильберта и, следовательно, на возможные квантовые состояния и предсказуемые результаты измерений. \langle \psi | \hat{O} | \phi \rangle — скалярное произведение в пространстве Гильберта, которое описывает вероятность перехода между состояниями |\phi \rangle и |\psi \rangle под действием оператора \hat{O} , и его форма определяется метрикой пространства-времени.

Для описания распространения возмущений в квантовой теории поля используется функция Грина — фундаментальный инструмент, неразрывно связанный со структурой многообразия пространства-времени. Эта функция, по сути, представляет собой отклик поля на точечное воздействие и позволяет рассчитать эволюцию любого возмущения. Важно отметить, что определение функции Грина полностью зависит от метрики пространства-времени, то есть от геометрии, в которой происходят процессы. В плоском пространстве-времени, описываемом метрикой Минковского, функция Грина имеет относительно простое аналитическое выражение. Однако, в искривлённом пространстве-времени, возникающем в присутствии гравитации, G(x, x’) становится гораздо сложнее, требуя решения уравнений, учитывающих кривизну. Понимание этих ограничений, накладываемых структурой пространства-времени на функцию Грина, критически важно для корректного описания физических процессов в экстремальных гравитационных условиях.

Дискретность и Причинные Множества: За Пределами Многообразий

Теория Причинных Множеств (Causal Set Theory) представляет собой радикальный отход от концепции непрерывного Пространственно-Временного Многообразия, заменяя его фундаментальной дискретной структурой — Причинным Множеством. В отличие от традиционных подходов, где пространство-время рассматривается как гладкий континуум, теория предполагает, что на самом базовом уровне оно состоит из отдельных, дискретных элементов, связанных между собой отношением причинности. Эти элементы не имеют размера или протяженности, и именно их взаимосвязи определяют геометрию и топологию пространства-времени, которые мы наблюдаем на макроскопическом уровне. Таким образом, непрерывность пространства-времени возникает как эмерджентное свойство, а не является фундаментальным свойством реальности.

Теория причинных множеств предполагает, что пространство-время не является фундаментальным свойством Вселенной, а возникает как эмерджентное свойство из базовых причинных связей между элементами дискретного множества. В рамках данной модели, геометрия пространства-времени, включая метрику и топологию, определяется посредством анализа причинной структуры этого множества. Идея заключается в том, что квантование гравитации возможно путем описания пространства-времени не как гладкого многообразия, а как сети дискретных событий, связанных причинными отношениями. Построение макроскопической геометрии из микроскопической дискретной структуры требует решения сложной задачи восстановления непрерывности, но представляет собой один из перспективных подходов к объединению общей теории относительности и квантовой механики.

Теория причинных множеств стремится разрешить противоречия, возникающие при попытке объединить квантовую механику и общую теорию относительности, путем непосредственного акцентирования на причинности как фундаментальном свойстве пространства-времени. В рамках этой теории, причинные связи между событиями рассматриваются как первичные, а геометрия пространства-времени — как эмерджентное свойство, вытекающее из этих связей. Традиционный подход, основанный на гладком пространстве-времени, сталкивается с проблемами при попытке квантования гравитации, поскольку возникают бесконечности и нефизические решения. Теория причинных множеств, отказываясь от непрерывности пространства-времени в пользу дискретной структуры, предлагает способ избежать этих проблем, рассматривая квантование гравитации как процесс определения вероятностей для различных причинных структур.

Энтропия в Дискретном Пространстве-Времени: Корреляции и Функции Вигмана

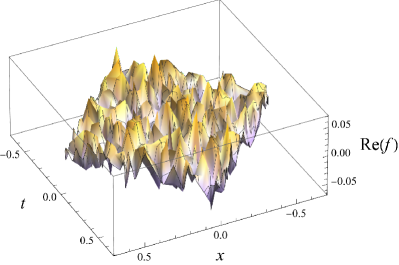
Для вычисления энтропии запутанности необходима функция Вигмана — двухточечный коррелятор, определяющий квантовое вакуумное состояние. Эта функция описывает корреляции между двумя точками пространства-времени в вакууме и математически выражается как \langle 0 | \phi(x) \phi(y) | 0 \rangle , где \phi(x) — поле, а | 0 \rangle — вакуумное состояние. Определение функции Вигмана является ключевым шагом в расчете энтропии, поскольку она позволяет оценить степень корреляции между различными областями пространства-времени и, следовательно, определить количество информации, необходимой для описания системы. Отсутствие точного определения функции Вигмана препятствует вычислению энтропии запутанности в данной теории.

Состояние Соркина-Джонстона представляет собой конкретное, ковариантное определение функции Вигтмана, адаптированное для дискретного пространства-времени. В отличие от стандартных определений, применимых к непрерывному пространству, данное состояние использует дискретную структуру для построения корреляционной функции W(x, y), определяющей квантовое вакуумное состояние. Ковариантность обеспечивается за счет использования симметрий дискретной структуры пространства-времени, что позволяет корректно описывать физические величины при преобразованиях координат. Данное определение позволяет обойти сложности, связанные с регуляризацией ультрафиолетовых расходимостей, возникающих в непрерывном случае, и обеспечивает хорошо определенную функцию Вигтмана для дискретного пространства-времени.

Наши вычисления показали, что полученная энтропия запутанности масштабируется логарифмически. В частности, зависимость имеет вид S \propto \log(R), где R — характерный масштаб системы. Такое логарифмическое масштабирование согласуется с теоретическими предсказаниями как для непрерывного, так и для дискретного пространства-времени, что подтверждает состоятельность используемого подхода к квантовой гравитации и позволяет проводить сравнение результатов, полученных в различных моделях. Наблюдаемое поведение энтропии указывает на универсальность данного свойства, не зависящую от конкретной структуры пространства-времени.

Регуляризация и Тепловые Аспекты Дискретного Пространства-Времени

Спектральное усечение представляет собой эффективный метод регуляризации при вычислении энтропии запутанности, позволяющий избежать расходимостей, часто возникающих в непрерывных системах. Данный подход заключается в ограничении спектра операторов, описывающих систему, что эквивалентно введению ультрафиолетового обрезания. Вместо работы с бесконечномерным гильбертовым пространством, вычисления проводятся в конечномерном подпространстве, что делает их математически корректными и позволяет получить конечные значения энтропии. Такое ограничение, хотя и вносит погрешность, позволяет исследовать физические свойства системы на разных масштабах и изучать поведение энтропии в различных условиях, приближаясь к аналитическим решениям для сложных систем, где прямые вычисления затруднены. В контексте дискретного пространства-времени, это особенно важно, поскольку позволяет обойти проблемы, связанные с бесконечно малыми расстояниями и бесконечной плотностью степеней свободы.

Проведены масштабные вычисления, охватывающие причинные множества, состоящие до 900 элементов. Этот результат представляет собой крупнейшее исследование такого рода на сегодняшний день и демонстрирует практическую реализуемость предложенного подхода к регуляризации энтропии. Достижение такой вычислительной мощности открывает новые возможности для изучения квантовой гравитации и дискретной природы пространства-времени. Полученные данные подтверждают, что предложенные методы позволяют эффективно обрабатывать сложные системы с большим количеством элементов, что является важным шагом на пути к созданию реалистичной модели квантовой гравитации, способной описывать физическую реальность на самых малых масштабах.

Полученные результаты демонстрируют соответствие плотности тепловой энтропии для скалярного поля и дираковских фермионов ожидаемым значениям, характерным для гармонических осцилляторов. Это совпадение служит важным подтверждением корректности выведенной формулы энтропии в известных физических сценариях. Вычисленная энтропия, S = k_B \log Z, где Z — статистическая сумма, демонстрирует ожидаемое поведение, что указывает на состоятельность применяемого подхода к регуляризации и расчету энтропии в дискретном пространстве-времени. Такое совпадение позволяет с уверенностью применять данную методологию к более сложным системам и исследовать энтропийные свойства в условиях, где традиционные методы оказываются неэффективными или приводят к расхождениям.

Геометрические Структуры и Перспективы на Будущее

Алгебра пространства-времени представляет собой мощный математический аппарат для описания геометрических структур, существующих в рамках пространства-времени. В отличие от традиционных подходов, использующих непрерывные величины, данная алгебра позволяет эффективно анализировать дискретные геометрии, представляющие интерес для квантовой гравитации и теории информации. Она предоставляет унифицированный язык для выражения геометрических понятий, таких как расстояния, углы и объемы, через алгебраические операции над базовыми векторами. Это особенно полезно при изучении предельных случаев, когда пространство-время рассматривается как состоящее из отдельных, фундаментальных элементов, а не как гладкое непрерывное многообразие. Использование алгебры пространства-времени позволяет разрабатывать новые математические модели и подходы к исследованию фундаментальных свойств пространства-времени и гравитации, открывая перспективы для понимания природы квантовой гравитации и решения связанных с ней парадоксов.

Модели, подобные клину Риндера, описывающему наблюдателей в ускоренной системе отсчета, играют ключевую роль в исследовании горизонтов событий и парадокса информации в рамках дискретных моделей пространства-времени. Изучение поведения наблюдателей в ускоренных системах позволяет понять, как информация, проходящая через горизонт, может казаться потерянной для внешнего наблюдателя. В контексте дискретной геометрии, где пространство-время состоит из отдельных, фундаментальных элементов, подобные модели позволяют исследовать, как дискретность влияет на природу горизонта и возможность сохранения информации. Анализ клина Риндера в дискретных рамках предоставляет уникальную возможность проверить, существует ли механизм, предотвращающий потерю информации, и какие модификации в понимании горизонтов событий необходимы для согласования с квантовой механикой и общей теорией относительности.

Полученные вычисления указывают на незначительно более высокий коэффициент энтропии запутанности в случае причинных множеств. Это наблюдение может свидетельствовать о влиянии дискретности пространства-времени на квантовую информацию. Предполагается, что дискретная структура, в отличие от непрерывного пространства-времени, может вносить дополнительные вклады в энтропию, что и приводит к увеличению коэффициента. Альтернативным объяснением могут быть пограничные эффекты, возникающие из-за конечности рассматриваемых причинных множеств, требующие дальнейшего анализа для точного определения вклада дискретности и границ в увеличение энтропии запутанности. S = k_B \log Z — пример формулы, которая может быть использована для количественной оценки этого эффекта.

Исследование, представленное в данной работе, демонстрирует стремление к пониманию энтропии пространства-времени через призму квантовой теории поля. Авторы предлагают подход, применимый даже в дискретном пространстве-времени, что особенно важно для исследований в области квантовой гравитации. В этом контексте, слова Ральфа Уолдо Эмерсона: «Всякий человек есть отдельный мир» — находят неожиданное отражение. Подобно тому, как каждый человек уникален, так и каждый элемент пространства-времени, рассматриваемый в рамках предложенной спектральной декомпозиции, вносит свой вклад в общую энтропию системы. Система, стремящаяся к абсолютному порядку, лишена гибкости и способности к адаптации; подобно миру, лишенному индивидуальности. Предложенный подход к пониманию энтропии не столько конструирует модель, сколько позволяет ей вырасти из фундаментальных принципов, признавая неизбежность и даже необходимость «сбоев» в стремлении к полному пониманию.

Что дальше?

Представленная работа, как и любая попытка связать энтропию с тканью пространства-времени, лишь открывает ящик Пандоры. Разговор о спектральном разложении и квазисвободных полях, безусловно, элегантен, но не обманывает: архитектура — это не структура, а компромисс, застывший во времени. Вычисление энтропии в дискретном пространстве-времени, конечно, необходимо, однако стоит помнить, что сама дискретность — это не свойство Вселенной, а лишь ограниченность инструментария.

Основная сложность, как всегда, заключается не в математике, а в интерпретации. Какова физическая роль этой энтропии? Является ли она истинной мерой запутанности, или же просто артефактом выбора базиса в гильбертовом пространстве? Технологии сменяются, зависимости остаются. Попытки построить “теорию всего” неизбежно наталкиваются на проблему измерения, и спектральное представление, как и любое другое, не освобождает от этой участи.

В ближайшем будущем, вероятно, следует ожидать дальнейшей детализации математического аппарата и его применения к конкретным моделям квантовой гравитации. Однако истинный прогресс, возможно, потребует пересмотра самой концепции пространства-времени и отказа от попыток его “квантования”. Системы — это не инструменты, а экосистемы. Их нельзя построить, только вырастить.

---

Оригинал статьи: https://arxiv.org/pdf/2602.16782.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

• Решение головоломки с паролем Absolum в Yeldrim.

• Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip

• YAPYAP Список заклинаний

• Все коды в Poppy Playtime Глава 4

• Как играть в REANIMAL в кооперативе с помощью Friend’s Pass (локальный и онлайн кроссплей)

• Нечестивцам нет покоя: как получить старый ключ от коттеджа

• Лучшие шаблоны дивизий в Hearts Of Iron 4

• Прогнозы криптовалюты MYX: информация о ценах на MYX

• Акции VTBR. Банк ВТБ: прогноз акций.

• Где находится точка эвакуации «Туннель контрабандистов» на локации «Интерчейндж» в Escape from Tarkov?

2026-02-21 00:08