Фазовые переходы в КХД: новый взгляд на критическую точку

Автор: Денис Аветисян

Исследование объединяет модель Намбу-Джона-Ласинио и подход Курчи-Феррари для детального изучения фазового перехода от хиральной симметрии к деконфайнменту в квантовой хромодинамике.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

Диаграмма фаз, построенная на основе инфлексных точек изменения числа кварков <span class="katex-eq" data-katex-display="false">\Delta Q_{q+1}</span> и <span class="katex-eq" data-katex-display="false">\Delta Q_{\bar{q}-1}</span>, демонстрирует псевдокритические температуры и положение хирального перехода, где скачки между значениями ±3 и ±1 для кваркового зонда указывают на точки критических изменений и расходимости вблизи критической точки, отражая процесс поглощения пробных частиц средой. — Диаграмма фаз, построенная на основе инфлексных точек изменения числа кварков $\Delta Q_{q+1}$ и $\Delta Q_{\bar{q}-1}$ , демонстрирует псевдокритические температуры и положение хирального перехода, где скачки между значениями ±3 и ±1 для кваркового зонда указывают на точки критических изменений и расходимости вблизи критической точки, отражая процесс поглощения пробных частиц средой.

В статье представлена комбинированная модель, использующая потенциал петли Полякова на основе подхода Курчи-Феррари, для исследования КХД-диаграммы фаз и идентификации критической точки.

Несмотря на значительный прогресс в изучении фазовой структуры КХД, точное определение взаимосвязи между спонтанным нарушением хиральной симметрии и переходом конфайнмент-деконфайнмент остается сложной задачей. В данной работе, озаглавленной ‘Interplay between the chiral and deconfinement transitions from a Curci-Ferrari-based Polyakov loop potential’, предложена комбинированная модель, объединяющая двухвкусительную модель Намбу-Йона-Ласинио с подходом, основанным на модели Курчи-Феррари, для исследования фазовой диаграммы КХД. Полученные результаты демонстрируют возможность построения согласованной картины фазовых переходов и позволяют исследовать термодинамические величины, включая чувствительный к фазовой структуре отклик среды на изменение плотности барионного числа. Каким образом уточнение параметров в предложенной модели позволит более точно определить критическую точку и характеристики различных фаз КХД?

Загадка КХД: Конфайнмент и Кварк-Глюонная Плазма

Квантовая хромодинамика (КХД), фундаментальная теория сильных взаимодействий, предсказывает существование перехода между состоянием, в котором кварки и глюоны заключены внутри адронов, и состоянием, где они свободно распространяются как кварк-глюонная плазма. Однако, детали этого перехода, а именно точная температура и плотность, при которых он происходит, остаются предметом интенсивных исследований. Сложность заключается в том, что при энергиях, соответствующих этому переходу, стандартные методы теории возмущений, успешно применяемые в других областях физики элементарных частиц, оказываются неэффективными. Понимание этого перехода имеет ключевое значение для реконструкции условий, существовавших в первые моменты после Большого взрыва, а также для изучения свойств сверхплотной материи, содержащейся в нейтронных звездах. Изучение этого феномена требует применения сложных непертурбативных методов, таких как решетка КХД и методы функционального ренормализационной группы, что делает его одной из самых актуальных и сложных задач современной физики.

При изучении перехода между заключенным и деконфинированным состоянием кварк-глюонной материи, предсказанного квантовой хромодинамикой (КХД), стандартные методы теории возмущений оказываются неэффективными. Это связано с тем, что энергии, характерные для данного перехода, находятся за пределами области применимости этих методов. Сильное взаимодействие между кварками и глюонами при высоких энергиях требует использования непертурбативных подходов, таких как решетчатая КХД и функциональные методы. Эти методы позволяют учитывать сложные нелинейные эффекты и исследовать поведение системы в условиях, где теория возмущений неприменима, что необходимо для понимания фазовых свойств кварк-глюонной плазмы и ее роли в экстремальных астрофизических условиях.

Характер перехода между фазами кварк-глюонной материи — плавный кроссовер или переход первого рода — имеет глубокие последствия для понимания ранней Вселенной и физики нейтронных звезд. В случае кроссовера, Вселенная могла остывать постепенно, без резких изменений в плотности и составе материи. Однако, если переход является фазовым переходом первого рода, возникают условия для образования пузырей новой фазы, что могло привести к бурным процессам и повлиять на формирование структуры Вселенной. Что касается нейтронных звезд, то характер этого перехода определяет их внутреннюю структуру и стабильность. Переход первого рода может приводить к образованию экзотических состояний материи внутри звезды, а также влиять на частоту и амплитуду гравитационных волн, излучаемых при столкновениях нейтронных звезд. Таким образом, точное определение характера этого фазового перехода является ключевой задачей для современной физики высоких энергий и астрофизики.

Зависимость параметров упорядочения от температуры при химическом потенциале <span class="katex-eq" data-katex-display="false">\mu=M_0 \sim eq 336</span> МэВ, соответствующем вакуумной массе кварка, демонстрирует прохождение через спинодальную область, при этом тонкие линии обозначают метастабильные и неустойчивые экстремумы, а заполненные и пустые точки - фазовый переход первого рода и дополнительные точки перегиба соответственно. — Зависимость параметров упорядочения от температуры при химическом потенциале $\mu=M_0 \sim eq 336$ МэВ, соответствующем вакуумной массе кварка, демонстрирует прохождение через спинодальную область, при этом тонкие линии обозначают метастабильные и неустойчивые экстремумы, а заполненные и пустые точки — фазовый переход первого рода и дополнительные точки перегиба соответственно.

Моделирование Нарушения Симметрии: Подходы NJL и PNJL

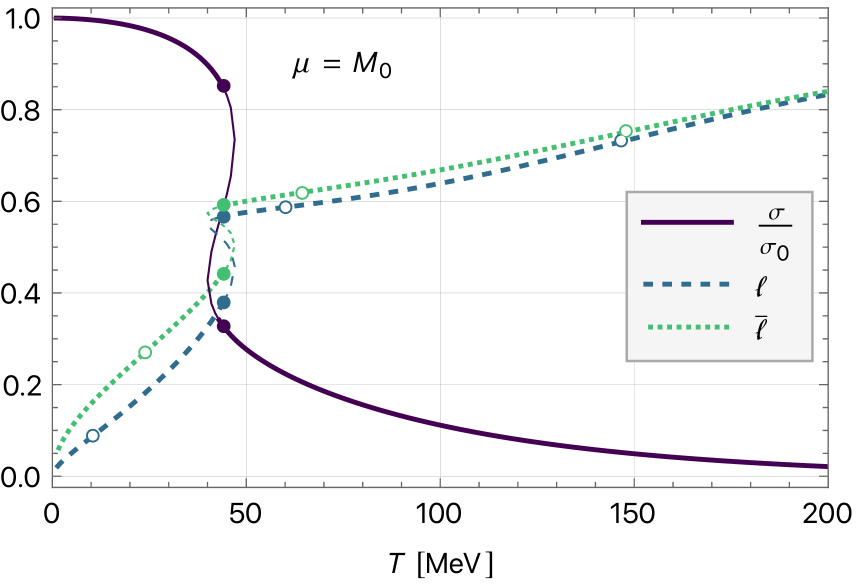
Модель Намбу-Джона-Ласинио (NJL) предоставляет теоретическую основу для изучения спонтанного нарушения хиральной симметрии, являющегося ключевым аспектом конфайнмент-фазы. В рамках этой модели, взаимодействие кварков описывается четырехфермионным взаимодействием, приводящим к образованию динамической массы кварков даже при нулевой «голой» массе. Это нарушение симметрии проявляется в образовании конденсата кварков $\langle \bar{q}q \rangle$ , который не равен нулю в вакууме, что является индикатором спонтанного нарушения хиральной симметрии и, как следствие, конфайнмента кварков. Модель NJL позволяет исследовать свойства этой динамической массы и конденсата кварков, а также их зависимость от параметров взаимодействия и температуры.

Модель Намбу-Джона-Ласинио (NJL), несмотря на свою эффективность в описании спонтанного нарушения хиральной симметрии, не содержит встроенного механизма для непосредственного описания конфайнмента и деконфайнмента кварков и глюонов. Это ограничение преодолевается путем введения петли Полякова (Polyakov loop) — непертурбативного параметра, являющегося индикатором конфайнмента. Петля Полякова, как динамическая переменная порядка, позволяет отслеживать переход между конфайнментной и деконфайнментной фазами, дополняя описание хирального фазового перехода, осуществляемого в рамках NJL модели. $\langle W \rangle$ — обозначение петли Полякова, где $W$ — оператор упорядочения пути для глюонного поля.

Модель PNJL объединяет модель Намбу-Джона-Ласинио (NJL) с петлей Полякова, предоставляя динамический параметр порядка для перехода конфайнмент-деконфайнмент. Петля Полякова, представляющая собой след оператора порядка, описывает поведение кварков в условиях сильного взаимодействия и служит индикатором свободы кварков. Комбинация NJL и петли Полякова позволяет исследовать как нарушение хиральной симметрии, характерное для конфайнментной фазы, так и фазовый переход между конфайнментной и деконфайнментной фазами. В рамках модели PNJL, эффективный потенциал, учитывающий взаимодействие между кварками и петлей Полякова, позволяет рассчитывать температуру и химический потенциал, при которых происходит переход между фазами, а также исследовать влияние различных параметров на фазовую диаграмму адронной материи.

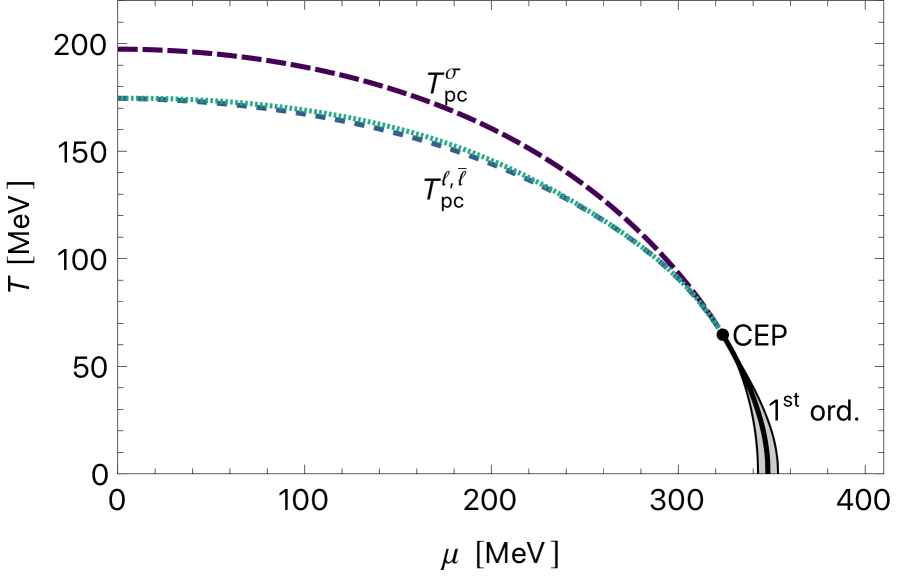
Фазовая диаграмма модели csCF-PNJL на плоскости <span class="katex-eq" data-katex-display="false">(\mu, T)</span> демонстрирует коэксистенцию фаз и критическую точку, определяемые пересечениями различных параметров порядка σ, <span class="katex-eq" data-katex-display="false">\ell</span> и <span class="katex-eq" data-katex-display="false">\bar{\ell}</span>, которые сходятся в спинодальную область и область первого порядка перехода. — Фазовая диаграмма модели csCF-PNJL на плоскости $(\mu, T)$ демонстрирует коэксистенцию фаз и критическую точку, определяемые пересечениями различных параметров порядка σ, $\ell$ и $\bar{\ell}$ , которые сходятся в спинодальную область и область первого порядка перехода.

Уточнение Модели: Включение Динамики Калибровочных Полей

Для повышения точности и реалистичности модели PNJL необходимо включение аспектов динамики калибровочных полей. Исходная PNJL модель, будучи эффективной теорией, упрощает описание взаимодействия кварков и глюонов, не учитывая в полной мере непертурбативные эффекты, связанные с конфайнментом. Включение динамики калибровочных полей позволяет более адекватно описывать взаимодействие между кварками посредством глюонов, что критически важно для корректного воспроизведения фазовых переходов между адронной материей и кварк-глюонной плазмой. Такой подход позволяет учитывать влияние вакуумных флуктуаций глюонов и их вклад в массу кварков, что необходимо для получения физически обоснованных результатов, особенно в области высоких температур и плотностей.

Модель Курчи-Феррари представляет собой систематический подход к проблеме конфайнмента, обеспечивающий уточнение обработки непертурбативных эффектов в квантовой хромодинамике. В отличие от пертурбативных методов, которые становятся неточными при низких энергиях и больших расстояниях, модель Курчи-Феррари использует эффективные взаимодействия, возникающие из непертурбативных конфигураций глюонов. Ключевым элементом является введение дополнительных глюонных полей, позволяющих учесть влияние вакуумных флуктуаций и динамического формирования глюонных конденсатов. Это приводит к модификации пропагатора глюона и, как следствие, к эффективному экранированию цветового заряда, что является необходимым условием для конфайнмента кварков и глюонов. Данный подход позволяет систематически улучшать описание непертурбативной динамики и получать более точные предсказания для различных наблюдаемых, связанных с конфайнментом и деконфайнментом адронной материи.

Интеграция элементов модели Курчи-Феррари в рамки PNJL (Поляризованной модели Нюджимы-Джонса) направлена на более точное описание динамики конфайнмента и деконфайнмента кварков и глюонов. В данном исследовании, путем анализа точек перегиба параметров упорядоченности, был определен критический конец фазового перехода при приближенных значениях (324 МэВ, 64 МэВ). Это позволяет получить более достоверные предсказания относительно свойств кварк-глюонной плазмы и фазового перехода между адронной материей и кварк-глюонной плазмой, учитывая непертурбативные эффекты, характерные для сильных взаимодействий.

Положение центра равнодействующей силы (CEP) смещается при изменении масштаба перенормировки ξ в диапазоне [0.1, 5] ГэВ для как для параметров, полученных из чистой ЯМ теории, так и для параметров, полученных из подгонки по данным КХД, при этом заполненные символы показывают предельные значения <span class="katex-eq" data-katex-display="false">\xi=0</span>. — Положение центра равнодействующей силы (CEP) смещается при изменении масштаба перенормировки ξ в диапазоне [0.1, 5] ГэВ для как для параметров, полученных из чистой ЯМ теории, так и для параметров, полученных из подгонки по данным КХД, при этом заполненные символы показывают предельные значения $\xi=0$ .

Вызовы и Перспективы: К Реалистичным Симуляциям

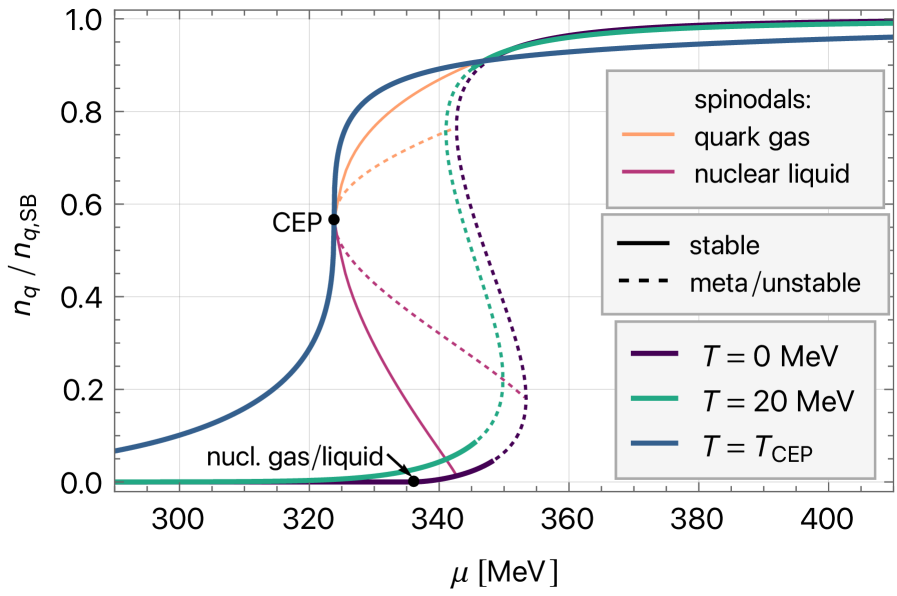
Исследование поведения системы при ненулевом химическом потенциале, что имеет решающее значение для понимания нейтронных звезд и столкновений тяжелых ионов, сталкивается с серьезным препятствием, известным как “Проблема знака” в рамках решетчатой квантовой хромодинамики (КХД). Эта проблема возникает из-за осциллирующей природы определителя матрицы Ферми, возникающего в функциональном интеграле, что приводит к экспоненциальному росту статистического шума при попытке численного моделирования. Вследствие этого, методы Монте-Карло, обычно используемые для решения уравнений КХД, становятся неэффективными при ненулевом химическом потенциале, поскольку требуют огромного количества вычислительных ресурсов для получения достоверных результатов. Фактически, “Проблема знака” ограничивает возможность точного изучения фазовых переходов и свойств материи при экстремальных условиях, существующих в ядрах нейтронных звезд и в результате столкновений тяжелых ионов, что требует разработки новых подходов и методов для преодоления данного ограничения.

Уравнение состояния, имеющее решающее значение для понимания термодинамических свойств кварк-глюонной плазмы, представляет собой значительную вычислительную проблему. Точное его определение затруднено из-за так называемой «проблемы знака» в решетчатой квантовой хромодинамике (КХД), которая приводит к экспоненциальному росту вычислительных затрат при попытке моделирования системы при ненулевом химическом потенциале. Это особенно актуально для условий, существующих в нейтронных звездах и при столкновениях тяжелых ионов, где химический потенциал может быть значительным. В результате, получение надежных данных об уравнении состояния требует разработки и использования альтернативных подходов, таких как модель ПНЮЛ, которая, хотя и является упрощением, позволяет получить ценные представления и служит ступенькой к более сложным и точным вычислениям. Построение надежного уравнения состояния является ключевым для понимания фазовых переходов и коллективного поведения кварк-глюонной материи.

Модель PNJL, являясь важным этапом в изучении кварк-глюонной плазмы, предоставляет ценные сведения, служа отправной точкой для более сложных подходов. Данное исследование установило псевдокритическую температуру около 175 МэВ, определяемую по точке перегиба температурной восприимчивости параметров упорядочения. При этом рассчитанное значение $nq/T^3$ отклоняется примерно на 15% от данных решетчатой КХД для $N_f=2$ при $T=2T_{pc}$ . Скорость звука ( $cs^2$ ) при высоких температурах стремится к 1/3, согласуясь с данными решетчатой КХД, экстраполированными к пределу непрерывности для $N_f=2+1$ , а аномалия следа ( $\epsilon-3p$ )/ $T^4$ качественно воспроизводится. Полученные результаты подтверждают перспективность дальнейшего развития модели для углубленного понимания свойств кварк-глюонной материи.

В спинодальной области плотность кварков, нормированная к значению насыщения, демонстрирует переход между фазами, характеризующимися сломанной (∼ ядерная жидкость, пурпурный) и восстановленной (∼ кварковая плазма, оранжевый) хиральной симметрией, что отражено линиями, исходящими от критической точки и достигающими значений при <span class="katex-eq" data-katex-display="false">T=0</span>. — В спинодальной области плотность кварков, нормированная к значению насыщения, демонстрирует переход между фазами, характеризующимися сломанной (∼ ядерная жидкость, пурпурный) и восстановленной (∼ кварковая плазма, оранжевый) хиральной симметрией, что отражено линиями, исходящими от критической точки и достигающими значений при $T=0$ .

Представленная работа демонстрирует, как попытки моделирования сложных систем, таких как фазовая диаграмма КХД, неизбежно включают в себя упрощения и акцентирование определенных аспектов реальности. В стремлении к математической строгости и предсказуемости, исследователи, по сути, создают проекцию, отражающую не абсолютную истину, а лишь определенный взгляд на неё. Как метко заметил Мишель Фуко: «Знание не строится на истине, а на отношениях силы». В данном случае, сила заключается в выбранном методе моделирования — комбинации модели Намбу-Джона-Ласинио и подхода Курчи-Феррари. Несмотря на свою эффективность в описании критической точки и поведения термодинамических величин, эта модель, как и любая другая, является лишь одной из возможных интерпретаций, подверженной ограничениям и предвзятостям.

Куда же это всё ведёт?

Представленная работа, как и большинство попыток картографировать фазовую диаграмму КХД, оперирует с надеждой на предсказуемость. Однако, следует помнить, что модель — это не отражение реальности, а лишь способ упорядочить собственные ожидания. Использование комбинации моделей NJL и Curci-Ferrari — это, по сути, признание недостатка одной единственной, всеобъемлющей теории. Эта «сшивка» позволяет лучше описывать некоторые наблюдаемые явления, но не устраняет фундаментальную неопределённость, присущую попыткам понять поведение кварк-глюонной плазмы.

Будущие исследования, вероятно, будут сосредоточены на усовершенствовании потенциалов, описывающих петлю Полякова. Однако, истинный прогресс потребует выхода за рамки стремления к точности. Необходимо признать, что критическая точка — это не просто координата на диаграмме, а область, где привычные представления о симметрии и разрыве симметрии терпят крах. Важно изучать не только термодинамические величины, но и флуктуации, корреляции, и другие «шумы», которые, возможно, содержат более глубокую информацию о структуре вакуума.

В конечном счёте, экономика физики, как и любая другая, заключается не в том, чтобы объяснить мир, а в том, чтобы объяснить надежды людей на контроль над ним. Моделирование — это не поиск истины, а создание иллюзии порядка в хаосе. И в этом нет ничего плохого — если помнить о границах этой иллюзии.

Оригинал статьи: https://arxiv.org/pdf/2601.15839.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-24 07:05