Фазовый сдвиг: Можно ли однозначно измерить эффект Берри по квантовым осцилляциям?

Автор: Денис Аветисян

Новое исследование показывает, что точное определение фазы Берри исключительно по данным квантовых осцилляций сопряжено со значительными трудностями и требует комплексного подхода.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал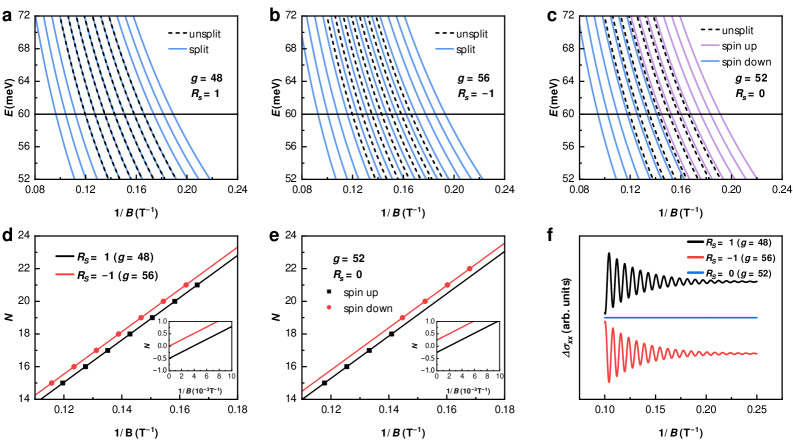

Влияние эффекта Зеемана на уровни Ландау демонстрирует, что при определенных параметрах - частоте осцилляций <span class="katex-eq" data-katex-display="false">F=129.5</span> T, энергии Ферми <span class="katex-eq" data-katex-display="false">E\_{F}=60</span> meV и эффективной массе <span class="katex-eq" data-katex-display="false">m^{*}=0.25m\_{0}</span> - сдвиг уровней, обусловленный эффектом Зеемана (<span class="katex-eq" data-katex-display="false">R_{s}=-1</span>), способен имитировать фазовый сдвиг π, характерный для нетривиальной фазы Берри (<span class="katex-eq" data-katex-display="false">\beta=0.5</span>), при этом полное подавление осцилляций наблюдается при <span class="katex-eq" data-katex-display="false">R_{s}=0</span>. — Влияние эффекта Зеемана на уровни Ландау демонстрирует, что при определенных параметрах — частоте осцилляций $F=129.5$ T, энергии Ферми $E\_{F}=60$ meV и эффективной массе $m^{*}=0.25m\_{0}$ — сдвиг уровней, обусловленный эффектом Зеемана ( $R_{s}=-1$ ), способен имитировать фазовый сдвиг π, характерный для нетривиальной фазы Берри ( $\beta=0.5$ ), при этом полное подавление осцилляций наблюдается при $R_{s}=0$ .

Анализ влияния фактора Ланде, сдвигов уровня Ферми и орбитального момента на интерпретацию результатов квантовых осцилляций в топологических материалах.

Несмотря на широкое использование квантовых осцилляций для определения фазы Берри, однозначное извлечение этой геометрической фазы остается сложной задачей. В работе, озаглавленной ‘Is it possible to determine unambiguously the Berry phase solely from quantum oscillations?’, показано, что интерпретация фазы осцилляций, основанная исключительно на данных Шубникова-де Гааса, подвержена неоднозначностям, обусловленным влиянием фактора спина и зависимостью уровня Ферми от магнитного поля. Полученные результаты демонстрируют, что пренебрежение этими факторами, особенно в топологических материалах с сильным спин-орбитальным взаимодействием, может приводить к ошибочным выводам о топологическом состоянии системы. Возможно ли разработать надежный экспериментальный подход, позволяющий точно определить фазу Берри и достоверно характеризовать топологические свойства материалов?

Квантовые Осцилляции: Зеркало Электронной Структуры

Квантовые осцилляции, такие как эффект Шубникова — де Гааса, представляют собой исключительно мощный инструмент для изучения Ферми-поверхности материалов. Этот эффект, проявляющийся в колебаниях электрического сопротивления в магнитных полях, позволяет с высокой точностью определить форму и размеры области в импульсном пространстве, доступной для электронов. По сути, анализ этих осцилляций дает возможность “отобразить” энергетическое распределение электронов, что крайне важно для понимания электрических, магнитных и тепловых свойств вещества. В частности, данный метод широко используется для исследования новых материалов, таких как сверхпроводники и топологические изоляторы, где форма Ферми-поверхности напрямую связана с их уникальными характеристиками и потенциальными применениями. $\hbar \omega_c = e \hbar B / m^*$ — эта базовая связь между частотой осцилляций, магнитным полем и эффективной массой электрона лежит в основе всего анализа.

Анализ фазы квантовых осцилляций, таких как эффект Шубникова — де Гааса, представляет собой сложную задачу, требующую глубокого понимания фундаментальных квантовомеханических факторов. Фаза осцилляции напрямую связана с волновой функцией электронов и их движением в периодическом потенциале кристаллической решетки. Точное определение фазы позволяет не только установить топологию поверхности Ферми, но и выявить влияние спин-орбитального взаимодействия, эффекта Зеемана и других квантовых явлений на поведение электронов. Игнорирование этих факторов может привести к существенным ошибкам в интерпретации результатов и искажению картины электронных свойств материала. Таким образом, детальный анализ фазы осцилляций является ключевым инструментом для исследования сложных квантовых систем и раскрытия их уникальных характеристик, особенно в контексте новых материалов с необычными электронными свойствами.

Точная интерпретация квантовых осцилляций, таких как эффект Шубникова — де Гааса, требует учета факторов, выходящих за рамки простого поведения носителей заряда. В реальности, на форму и фазу этих осцилляций влияют сложные взаимодействия между электронами, включая рассеяние на примесях и дефектах кристаллической решетки, а также эффекты, связанные с многочастичными корреляциями. Пренебрежение этими дополнительными вкладами может привести к неверному определению формы поверхности Ферми и, следовательно, к ошибочным выводам о свойствах материала. Тщательный анализ, включающий учет этих нюансов, позволяет более точно реконструировать электронную структуру и раскрыть потенциал новых материалов, обладающих уникальными физическими характеристиками. $\Delta H = \frac{nh}{m^<i>}$ — пример зависимости, где точное определение эффективной массы $m^</i>$ требует учета всех влияющих факторов.

Тонкости, проявляющиеся в квантовых осцилляциях, играют ключевую роль в раскрытии потенциала новых материалов. Анализ этих эффектов, выходящий за рамки простой модели поведения носителей заряда, позволяет исследователям получить детальную информацию о форме и топологии ферми-поверхности — фундаментальной характеристики, определяющей электронные свойства вещества. Именно учет сложных квантовомеханических факторов, влияющих на частоту и фазу осцилляций, дает возможность не только точно определить концентрацию и подвижность носителей, но и выявить экзотические электронные состояния, такие как дираковские конусы или топологические изоляторы. Таким образом, глубокое понимание этих нюансов становится необходимым условием для разработки материалов с заранее заданными и улучшенными характеристиками, открывая новые горизонты в области электроники и материаловедения.

Зависимость уровня Ферми от магнитного поля <span class="katex-eq" data-katex-display="false">E_{F}(B)</span> вызывает фазовый сдвиг в диаграмме Ландау, что может быть ошибочно интерпретировано как нетривиальная фаза Берри даже в тривиальных случаях, как для носителей с квадратичной (а), так и с линейной (б) дисперсией. — Зависимость уровня Ферми от магнитного поля $E_{F}(B)$ вызывает фазовый сдвиг в диаграмме Ландау, что может быть ошибочно интерпретировано как нетривиальная фаза Берри даже в тривиальных случаях, как для носителей с квадратичной (а), так и с линейной (б) дисперсией.

Теория Лифшица-Косевича: Ключ к Расшифровке Фазы Осцилляций

Теория Лифшица-Косевича является основополагающей структурой для интерпретации данных квантовых осцилляций, таких как осцилляции де Гааса и Шубникова-де Гааса. Она описывает зависимость магнитосопротивления от магнитного поля и позволяет определить ключевые характеристики носителей заряда в материале, включая эффективную массу $m^*$ и концентрацию носителей. В рамках данной теории, осцилляции возникают из-за квантования уровней Ландау в магнитном поле, а амплитуда и фаза этих осцилляций несут информацию о свойствах электронного состояния материала. Точность анализа данных напрямую зависит от корректного применения математического аппарата теории и учета различных факторов, влияющих на форму осцилляций.

Теория Лифшица-Косевича требует точного определения эффективной массы и спин-фактора носителей заряда для корректной интерпретации данных квантовых осцилляций. Эффективная масса $m^<i>$ характеризует инерцию носителя в кристаллической решетке и отличается от массы покоя из-за взаимодействия с периодическим потенциалом. Спин-фактор $g^</i>$ учитывает влияние спин-орбитального взаимодействия и магнитных свойств материала на частоту осцилляций. Неточное определение этих параметров приводит к ошибкам в расчете концентрации носителей и других важных характеристик материала, определяемых на основе данных квантовых осцилляций.

В рамках теории Лифшица-Косевича фаза квантовых осцилляций существенно модифицируется за счет включения эффекта Берри, геометрического явления, возникающего из-за изменений фазы волновой функции вдоль траектории движения носителей заряда в кристаллической решетке. Этот эффект проявляется как дополнительный вклад в общую фазу осцилляций, пропорциональный γ, — геометрической фазе Берри, которая зависит от топологических свойств электронного состояния и может принимать значения от 0 до π. Игнорирование фазы Берри может привести к неверной интерпретации данных и ошибочной оценке эффективной массы и спинового фактора носителей заряда. Учет этого геометрического вклада является критически важным для точного анализа и интерпретации результатов квантовых осцилляций.

Точность определения параметров, таких как эффективная масса и фактор спина носителей заряда, а также учет фазы Берри, критически важны для корректной интерпретации данных, полученных в экспериментах по квантовым осцилляциям. Отклонения в этих параметрах напрямую влияют на наблюдаемую частоту и амплитуду осцилляций, что может привести к неверной оценке концентрации носителей, геометрии поверхности Ферми и других ключевых характеристик материала. Применение теории Лифшица-Косевича позволяет установить количественную связь между теоретическими параметрами и экспериментальными данными, обеспечивая возможность извлечения значимой информации о физических свойствах исследуемого вещества. Недостаточное внимание к этим взаимосвязям может привести к существенным погрешностям в анализе и неверной интерпретации результатов.

Движение электронов по замкнутой траектории вблизи дираковской точки в зоне Бриллюэна приводит к приобретению нетривиальной π фазы Берри, аналогично переносу вектора по замкнутой петле на сфере.

Квантовые Осцилляции и Топологические Материалы: Раскрывая Необычные Свойства

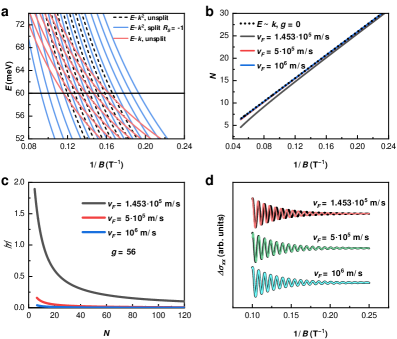
Точность вычисления фазы квантовых осцилляций существенно зависит от ряда факторов, выходящих за рамки базовой схемы Лифшица-Косевича. Помимо стандартных параметров, таких как циклотронная масса и время релаксации, необходимо учитывать влияние эффекта Зеемана, обусловленное фактором Ланде $g$ , который в некоторых материалах может достигать значений до 100. Геометрия орбит в пространстве обратных решеток требует внесения поправок Маслова для корректного расчета фазы. Кроме того, вклад орбитального магнитного момента и зависимость уровня Ферми от магнитного поля с коэффициентом $\alpha = 0.1 \text{ meV/T}$ оказывают значительное влияние на наблюдаемую картину квантовых осцилляций и требуют тщательного анализа.

Эффект Зеемана, определяемый фактором Ланде $g$ , оказывает существенное влияние на наблюдаемое поведение квантовых осцилляций. Значение фактора Ланде может значительно отклоняться от стандартного значения 2 для электронов, достигая в некоторых материалах величин до 100. Это отклонение связано со спин-орбитальным взаимодействием и приводит к пропорциональному изменению энергии уровней Зеемана, что, в свою очередь, изменяет период и фазу квантовых осцилляций. Необходимо учитывать значение фактора Ланде $g$ при анализе данных квантовых осцилляций для корректной интерпретации результатов и определения параметров материала.

Поправка Маслова учитывает геометрию орбит в обратном пространстве и необходима для точного расчета фазы квантовых осцилляций. В рамках теории Лифшица-Косевича, предположение о постоянстве площади орбиты в обратном пространстве не всегда справедливо, особенно при сильных магнитных полях или сложной форме поверхности Ферми. Поправка Маслова вносит поправку на изменение этой площади, вызванное искривлением орбит, что приводит к более точным расчетам фазы. Эффект наиболее заметен для орбит с большой эксцентриситетом и в материалах с высокой подвижностью носителей заряда. Неучет данной поправки может приводить к систематическим ошибкам в определении параметров поверхности Ферми и других физических характеристик материала.

Вклад орбитального магнитного момента необходимо учитывать при расчете фазы квантовых осцилляций, поскольку он вносит дополнительный вклад в общую фазу. Кроме того, зеемановский эффект может индуцировать сдвиг фазы на π, что может быть ошибочно интерпретировано как наличие нетривиальной берри-фазы. Точный учет этих факторов критически важен для корректного анализа данных квантовых осцилляций и исключения ложных интерпретаций, связанных с геометрией траекторий носителей заряда в магнитном поле.

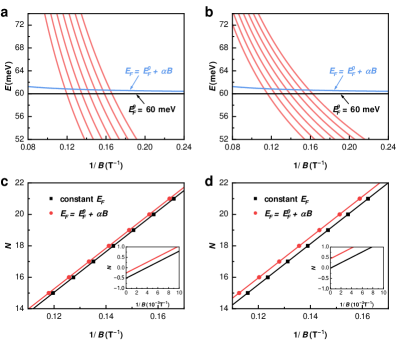
Уровень Ферми в исследуемых материалах демонстрирует зависимость от величины магнитного поля, характеризующуюся коэффициентом $\alpha = 0.1 \text{ meV/T}$ . Данная зависимость оказывает существенное влияние на положение точки пересечения с осью ординат на диаграмме Ландау (LL fan diagram). Изменение уровня Ферми, вызванное магнитным полем, приводит к сдвигу положений уровней Ландау и, как следствие, к модификации интерсепта, что необходимо учитывать при интерпретации данных квантовых осцилляций и определении параметров исследуемого материала.

Анализ энергетических зависимостей и диаграммы уровней Ландау для фермионов с квадратичной и линейной дисперсией показывает влияние расщепления уровней и скорости Ферми <span class="katex-eq" data-katex-display="false">v_F</span> на осциллирующие компоненты проводимости <span class="katex-eq" data-katex-display="false">\Delta\sigma_{xx}</span>. — Анализ энергетических зависимостей и диаграммы уровней Ландау для фермионов с квадратичной и линейной дисперсией показывает влияние расщепления уровней и скорости Ферми $v_F$ на осциллирующие компоненты проводимости $\Delta\sigma_{xx}$ .

Берри-Фаза и Топологические Материалы: Новые Горизонты в Материаловедении

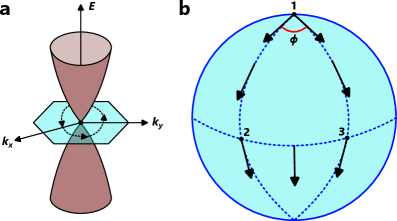
Берри-фаза играет фундаментальную роль в понимании необычных электронных свойств топологических материалов. Этот геометрический эффект, возникающий из-за изменений фазы волновой функции электрона при обходе в импульсном пространстве, определяет многие ключевые характеристики этих материалов. В отличие от обычных материалов, где электронные свойства определяются в основном энергией, в топологических материалах берри-фаза вносит существенный вклад, приводя к таким явлениям, как аномальный эффект Холла и защищенные поверхностные состояния. $\phi_{n} = i\in t_{C} \langle u_{n}| \nabla_{k} |u_{n} \rangle dk$ — данное выражение описывает берри-фазу, где интеграл берется по замкнутому контуру в импульсном пространстве. Изучение берри-фазы позволяет не только характеризовать топологическую структуру материалов, но и предсказывать и контролировать их электронные и транспортные свойства, открывая новые возможности для создания инновационных электронных устройств.

Квантовые осцилляции, в сочетании с теоретической основой Лифшица-Косевича, представляют собой мощный инструмент для детальной характеристики топологических материалов. Данный подход позволяет исследовать электронную структуру этих веществ, определяя форму и размер ферми-поверхности, а также выявляя особенности рассеяния электронов. Анализ частоты и фазы осцилляций, в рамках предложенной модели, предоставляет информацию о поперечном сечении Ферми-поверхности и эффективной массе носителей заряда. В частности, отклонения от стандартного поведения в рамках теории Лифшица-Косевича могут указывать на нетривиальную топологию электронных состояний и наличие новых физических явлений, таких как аномальный эффект Холла или защищенные поверхностные состояния. $\Delta H = \frac{2\pi}{\phi_0} \in t_{S} J(r) dS$ В результате, квантовые осцилляции служат своего рода «рентгеновским снимком» электронной структуры, раскрывая уникальные свойства этих перспективных материалов.

Анализ фазы колебаний, получаемых в квантовых осцилляционных экспериментах, представляет собой мощный инструмент для выявления нетривиальной топологии в материалах. Фаза колебаний напрямую связана с $\text{Berry Phase}$ — геометрической фазой, приобретаемой электронами в процессе обхода в импульсном пространстве. Отклонение фазы от целых или полуцелых значений указывает на наличие нетривиальной топологической структуры, что свидетельствует о существовании защищенных поверхностных состояний и необычных транспортных свойств. В частности, данный подход позволяет идентифицировать топологические изоляторы и полуметаллы Вейля, где $\text{Berry Phase}$ играет ключевую роль в формировании аномального эффекта Холла и других квантовых явлений, что делает анализ фазы колебаний незаменимым для характеристики новых материалов с экзотическими электронными свойствами.

Исследования передовых материалов, таких как вейлевские полуметаллы, демонстрируют, что фаза Берри играет определяющую роль в формировании необычных транспортных явлений. В этих материалах, характеризующихся особыми точками Дирака в структуре зон, фаза Берри, приобретенная электронами при обходе в импульсном пространстве, влияет на их движение принципиально новым образом. Наблюдаемые аномальные эффекты, включая отрицательное магнитосопротивление и хиральную аномалию, напрямую связаны с нетривиальной топологией электронных состояний и, следовательно, с фазой Берри. Этот эффект проявляется в том, что носители заряда ведут себя как безмассовые частицы, подверженные влиянию внешних полей и способные к необычным траекториям движения, что открывает перспективы для создания принципиально новых электронных устройств и материалов с уникальными свойствами.

Исследование, представленное в статье, подчеркивает сложность однозначного определения фазы Берри исключительно на основе измерений квантовых осцилляций. Подобно тому, как карта не может полностью отразить океан, так и теоретические модели оказываются недостаточными для полного понимания топологических состояний материи. Как заметил Альберт Эйнштейн: «Самое прекрасное, что мы можем испытать, — это тайна». Эта фраза находит отражение в неразрешенных трудностях, связанных с разделением вклада фазы Берри от различных эффектов, таких как сдвиги уровня Ферми и влияние орбитального момента. Неоднозначности, возникающие при определении g-фактора, служат напоминанием о пределах наших знаний и необходимости комплексного подхода к изучению квантовых явлений.

Что дальше?

Представленная работа, подобно мерцанию далекой звезды, лишь подчеркивает границы постигаемого. Стремление однозначно определить фазу Берри исключительно по квантовым осцилляциям оказалось задачей, полной скрытых переменных и неявностей. Фактор Ланде, смещения уровня Ферми, орбитальный момент, эффект Зеемана — каждый из этих элементов, подобно гравитационным волнам, искажает картину, уводя от истинного значения. Любая теория хороша, пока свет не покинет её пределы.

Становится очевидным, что надежная идентификация топологических состояний требует не единичного эксперимента, а сложного симбиоза различных методов. Изолировать фазу Берри, полагаясь лишь на колебания, — все равно что пытаться увидеть чёрную дыру напрямую. Необходимы дополнительные инструменты, позволяющие исследовать свойства материала под разными углами, словно окружая горизонт событий.

Чёрные дыры — идеальные учителя, они показывают пределы знания. Подобно им, эта работа демонстрирует, что в физике конденсированного состояния, как и в космологии, истина редко лежит на поверхности. Настоящий прогресс потребует не только усовершенствования экспериментальной техники, но и более глубокого философского осмысления самой природы измерения.

Оригинал статьи: https://arxiv.org/pdf/2601.09560.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-16 02:15