Геометрия и Топология Материалов: Новый Взгляд через Спектроскопию

Автор: Денис Аветисян

Исследователи предложили инновационный метод определения топологических свойств и квантовой геометрии материалов на основе анализа спектральных интенсивностей.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал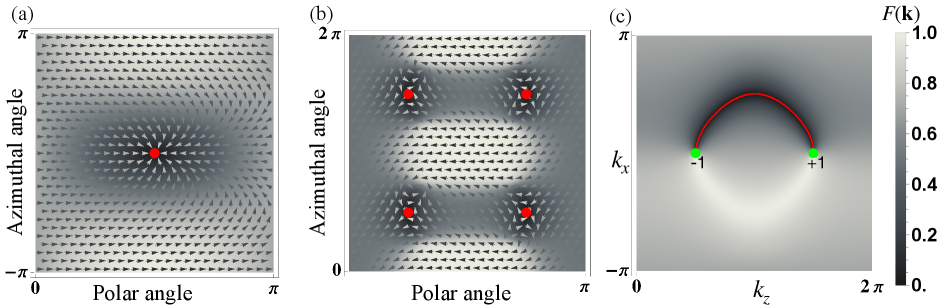

Топологическое правило отбора и узловые дуги для точек Вейля демонстрируют, что форма-фактор волновой функции, рассчитанный на различных многообразиях импульсного пространства, выявляет спектральные узлы, число которых соответствует заряду точки Вейля: вокруг точки с зарядом +1 образуется один узел, а вокруг квадрупольной точки с зарядом +4 - четыре, при этом суммарный индекс намотки узлов равен заряду, что подтверждается наличием спектральных дуг, соединяющих точки Вейля с противоположными зарядами на двумерных срезах зоны Бриллиуэна. — Топологическое правило отбора и узловые дуги для точек Вейля демонстрируют, что форма-фактор волновой функции, рассчитанный на различных многообразиях импульсного пространства, выявляет спектральные узлы, число которых соответствует заряду точки Вейля: вокруг точки с зарядом +1 образуется один узел, а вокруг квадрупольной точки с зарядом +4 — четыре, при этом суммарный индекс намотки узлов равен заряду, что подтверждается наличием спектральных дуг, соединяющих точки Вейля с противоположными зарядами на двумерных срезах зоны Бриллиуэна.

Новый подход позволяет напрямую измерять топологические инварианты и геометрические характеристики материалов через ‘фактор формы волновой функции’.

Несмотря на значительный прогресс в понимании топологических свойств конденсированных сред, прямое экспериментальное определение квантовой геометрии и топологии волновых функций остаётся сложной задачей. В работе, озаглавленной ‘Resolution of Topology and Geometry from Momentum-Resolved Spectroscopies’, предложен новый подход, основанный на анализе интенсивностей в спектроскопиях, разрешенных по импульсу и энергии. Вводится понятие “фактора формы волновой функции”, позволяющего извлекать топологические инварианты и геометрические характеристики материалов напрямую из экспериментальных данных. Позволит ли данная методика создать модель-независимый способ измерения кривизны Берри и квантрической метрики, открывая новые горизонты в исследовании материалов с необычными электронными свойствами?

Раскрытие топологии: новый взгляд на свойства материалов

Традиционный анализ зонной структуры, несмотря на свою широкую распространенность в материаловедении, зачастую оказывается неспособным выявить ключевые топологические особенности, определяющие свойства материалов. В то время как стандартные методы фокусируются на энергетических уровнях электронов, игнорируется геометрия волновых функций, несущая критически важную информацию о топологической защищенности состояний. Это приводит к упущению важных характеристик, таких как существование поверхностных состояний или необычных транспортных явлений. Игнорирование геометрических аспектов зонной структуры ограничивает возможности прогнозирования и управления свойствами материалов, особенно в контексте новых материалов с экзотическими электронными свойствами, где топологические эффекты играют решающую роль. В результате, понимание и контроль над этими свойствами требуют выхода за рамки традиционного подхода и учета топологической структуры электронных состояний.

Для полного описания электронной структуры материала недостаточно знать только энергию электронов в различных состояниях. Современное понимание требует учета геометрических свойств волновых функций, определяющих поведение электронов в кристалле. Волновая функция, описывающая электрон, не является просто скалярной величиной, а обладает сложной пространственной структурой, которая оказывает существенное влияние на физические свойства материала, такие как проводимость и оптические характеристики. Изучение этой геометрии позволяет выявить топологические особенности полосной структуры — фундаментальные характеристики, определяющие стабильность и уникальные свойства материала, которые не могут быть предсказаны при рассмотрении только энергетических уровней. Таким образом, понимание геометрической структуры волновых функций открывает новые возможности для разработки материалов с заданными свойствами и является ключевым шагом в развитии современной физики твердого тела.

Для полноценного понимания электронной структуры материалов недостаточно простого анализа точек пересечения энергетических зон. Истинное раскрытие топологических свойств требует более глубокого исследования — анализа перекрытия волновых функций электронов. Именно в тонкостях этого перекрытия кроется информация о геометрической структуре зон, определяющей многие физические характеристики вещества. Простое обнаружение точек, где энергетические зоны пересекаются, упускает важные детали, поскольку сама форма волновых функций, а не только их энергия, определяет топологическую структуру. Исследование перекрытия волновых функций позволяет выйти за рамки традиционного подхода и получить полное представление о топологии электронных зон, что открывает возможности для создания новых материалов с заданными свойствами.

Фактор формы волновой функции представляет собой мощный инструментарий для захвата геометрической информации и выявления топологических характеристик материалов. Исследования показали, что данный подход позволяет реконструировать топологию зонной структуры, основываясь исключительно на данных спектроскопии. Вместо анализа традиционных энергетических диаграмм, фактор формы волновой функции анализирует геометрию волновых функций, что дает возможность идентифицировать топологические инварианты, определяющие необычные электронные свойства. Этот метод позволяет определить, обладает ли материал нетривиальной топологией, которая может проявляться в виде защищенных поверхностных состояний или других экзотических явлений, даже если традиционные методы анализа зонной структуры не дают однозначного ответа. Таким образом, фактор формы волновой функции открывает новые возможности для исследования и понимания топологических материалов.

Расчеты детерминанта волновой функции <span class="katex-eq" data-katex-display="false">det[F(\mathbf{k})]</span> в <span class="katex-eq" data-katex-display="false">Cu_3TeO_6</span> подтверждают наличие нетривиального <span class="katex-eq" data-katex-display="false">Z_2</span> заряда, проявляющегося в виде спектрального узла на сфере, охватывающей точку Дирака <span class="katex-eq" data-katex-display="false">D_2</span>, и нодальной дуги, соединяющей <span class="katex-eq" data-katex-display="false">D_2</span> с ее партнером <span class="katex-eq" data-katex-display="false">D_3</span> в двумерном импульсном пространстве. — Расчеты детерминанта волновой функции $det[F(\mathbf{k})]$ в $Cu_3TeO_6$ подтверждают наличие нетривиального $Z_2$ заряда, проявляющегося в виде спектрального узла на сфере, охватывающей точку Дирака $D_2$ , и нодальной дуги, соединяющей $D_2$ с ее партнером $D_3$ в двумерном импульсном пространстве.

Экспериментальные методы зондирования геометрии волновых функций

Фотоэлектронная спектроскопия с разрешением по углу (ARPES) и неупругое рассеяние нейтронов являются ключевыми методами для экспериментального определения зонной структуры материалов. ARPES использует фотоэлектронный эффект для прямого картирования энергетической дисперсии электронов в кристалле, предоставляя информацию об электронных состояниях и их импульсе. Неупругое рассеяние нейтронов, в свою очередь, исследует колебания решетки и электронные возбуждения, позволяя определить дисперсию фононов и электронные спектры. Комбинирование данных, полученных с помощью ARPES и неупругого рассеяния нейтронов, обеспечивает комплексное представление о зонной структуре, необходимое для дальнейшего анализа и понимания физических свойств материала. Оба метода требуют ультравысокого вакуума и тщательно контролируемых условий для получения достоверных результатов.

Комбинированное применение спектроскопии фотоэмиссии, разрешенной по углу (ARPES), и неупругого рассеяния нейтронов позволяет экспериментально определить фактор формы волновой функции. Анализ данных, полученных этими методами, включает в себя моделирование углового распределения фотоэмиссионных интенсивностей и сечения неупругого рассеяния, что дает информацию о пространственном распределении электронов в кристалле. Точный расчет фактора формы требует учета кристаллической структуры, поляризации излучения и кинематики процесса, а также использования продвинутых методов обработки данных для отделения вклада различных электронных состояний и минимизации артефактов. Полученный фактор формы $F(q)$ характеризует амплитуду рассеяния электронов с волновым вектором $q$ и является ключевым параметром для понимания геометрии волновой функции.

Экспериментально полученный фактор формы волновой функции (Wavefunction Form Factor) является основой для понимания геометрии лежащей в основе волновой функции. Этот фактор, определяемый посредством спектроскопических методов, таких как спектроскопия фотоэмиссии, разрешенная по углу (ARPES) и неупругое рассеяние нейтронов, предоставляет информацию о пространственном распределении электронов в материале. Анализ фактора формы позволяет реконструировать форму волновой функции и выявить ее ключевые характеристики, включая симметрию и топологические особенности, что необходимо для понимания электронных свойств и поведения материала. Точность определения фактора формы напрямую влияет на адекватность моделирования и предсказания свойств исследуемого вещества.

Определение топологических особенностей в электронных структурах материалов становится возможным посредством картирования фактора формы волновой функции. Для точной идентификации этих особенностей требуется использование минимального количества зондов $Np$ , которое должно быть равно или превышать ранг проектора полосы $Nb$ . Это требование связано с необходимостью полного охвата релевантного пространства импульсов для корректного определения топологической структуры, где $Np$ представляет собой количество независимых измерений, а $Nb$ характеризует размерность пространства, описывающего проекцию волновой функции на конкретные состояния.

Геометрия узлового многообразия, определяемая правилом отбора, демонстрирует, что противоположно заряженные точечные заряды (например, точки Вейля) образуют одномерную узловую дугу (красный цвет), где интенсивность ARPES/INS равна нулю, а для узловых линий (зеленые петли) нули фазы π формируют двумерную узловую мембрану (красный цвет), а нули заряда <span class="katex-eq" data-katex-display="false"> Z_2 </span> образуют узловую трубку (синий цвет), соединяющую узловые линии с противоположными зарядами. — Геометрия узлового многообразия, определяемая правилом отбора, демонстрирует, что противоположно заряженные точечные заряды (например, точки Вейля) образуют одномерную узловую дугу (красный цвет), где интенсивность ARPES/INS равна нулю, а для узловых линий (зеленые петли) нули фазы π формируют двумерную узловую мембрану (красный цвет), а нули заряда $Z_2$ образуют узловую трубку (синий цвет), соединяющую узловые линии с противоположными зарядами.

Декодирование топологических сигнатур: спектральные узлы и за ее пределами

Топологическое правило отбора (Topological Selection Rule) предсказывает наличие нулей, известных как спектральные узлы (Spectral Nodes), в определителе волновой функции (Wavefunction Form Factor). Эти нули не случайны, а напрямую связаны с топологическими зарядами системы. Математически, наличие этих нулей является следствием специфических свойств волновой функции, обусловленных нетривиальной топологией электронных состояний. Определение расположения и количества этих узлов позволяет вычислить топологический заряд системы, что делает данный подход эффективным инструментом для классификации топологических состояний материи. $det(WFF) = 0$ указывает на наличие спектрального узла в точке k.

Спектральные узлы, возникающие в детерминанте формофактора волновой функции, служат надежными индикаторами нетривиальной топологии материала. Эти узлы представляют собой нули, которые устойчивы к небольшим возмущениям гамильтониана и, следовательно, являются прямым следствием топологических зарядов. Их наличие, а также степень каждого спектрального узла $d(k_i)$ , однозначно указывает на существование топологических состояний, позволяя идентифицировать топологические изоляторы и полуметаллы. Суммирование степеней всех спектральных узлов $\sum d(k_i)$ определяет полный топологический заряд (по модулю 2 для индексов $Z_2$ ), что подтверждает значимость спектральных узлов как ключевого инструмента в топологической классификации материалов.

Построение эффективного проектора полос на основе функции волнового фактора (Wavefunction Form Factor) позволяет детально исследовать и визуализировать топологические характеристики полосной структуры материала. Этот проектор, полученный из детерминанта функции волнового фактора, служит инструментом для идентификации и анализа топологических состояний, предоставляя возможность отобразить вклад различных волновых векторов в топологическую структуру. В частности, анализ проектора позволяет выявить области в импульсном пространстве, где проявляются топологические особенности, такие как поверхностные состояния или краевые моды, и количественно оценить их свойства. Использование проектора эффективно для визуализации топологически нетривиальных полос и понимания их влияния на электронные свойства материала.

Общий топологический заряд системы может быть определен путем суммирования степеней спектральных узлов $\sumd(ki) = total charge$ . Для систем с индексом Z2, полученная сумма берется по модулю 2, что позволяет однозначно определить топологический инвариант. Этот подход, основанный на правиле топологического отбора, предоставляет прямой и надежный метод вычисления топологического заряда, не требующий сложных вычислений или анализа волновой функции в каждой точке пространства. Степень каждого спектрального узла отражает вклад соответствующего топологического заряда в общую величину, делая суммирование степеней эффективным инструментом для характеристики топологических состояний вещества.

От топологии к функции: экзотические состояния и новая физика

Квантенный геометрический тензор, объединяющий в себе кривизну Берри и квантрическую метрику, играет фундаментальную роль в понимании реакции материалов на внешние воздействия. Этот тензор описывает геометрию волновой функции электронов в кристалле и определяет, как материал будет реагировать на электрические и магнитные поля, а также на деформации. Кривизна Берри отвечает за возникновение аномальных эффектов Холла, в то время как квантрическая метрика определяет скорость переноса заряда и влияет на оптические свойства материала. Понимание этих взаимосвязей позволяет предсказывать и контролировать поведение электронов, открывая перспективы для создания новых материалов с заданными функциональными характеристиками, например, с повышенной эффективностью преобразования энергии или уникальными оптическими свойствами. $\mathcal{Q}_{ij} = \langle \partial_i u | \partial_j u \rangle + i \epsilon_{ijk} \partial_k \phi$ — такая формализация позволяет количественно оценивать влияние геометрических свойств волновой функции на наблюдаемые физические величины.

Квантованная метрика, фундаментальное понятие в современной физике конденсированного состояния, определяет дисперсию плоских зон в электронных структурах материалов. Эта связь не ограничивается лишь теоретическим интересом; она напрямую проявляется в явлениях нелинейной оптики. В материалах с выраженными плоскими зонами, где квантованная метрика играет доминирующую роль, даже слабые внешние воздействия способны генерировать сильные нелинейные оптические отклики. Изучение влияния квантованной метрики на оптические свойства позволяет не только предсказывать и контролировать эти явления, но и открывает путь к созданию новых материалов с уникальными нелинейно-оптическими характеристиками, перспективных для разработки передовых оптических устройств и сенсоров. $g_{ij}$ — компоненты квантованной метрики, определяющие скорость изменения волновой функции в импульсном пространстве, что напрямую влияет на взаимодействие света с веществом.

Понимание топологических инвариантов, таких как число Черна и Z2-индекс, позволяет систематизировать различные фазы материи и предсказывать существование экзотических состояний. Эти инварианты, являющиеся глобальными характеристиками электронных волновых функций в кристалле, не зависят от локальных деталей материала и определяют его топологическую структуру. Например, ненулевое число Черна указывает на наличие краевых состояний, устойчивых к рассеянию на дефектах, что критически важно для создания надежных электронных устройств. В то время как Z2-индекс классифицирует топологические изоляторы, характеризующиеся проводящими поверхностными состояниями и изолирующим объемом. Исследование этих инвариантов открывает путь к разработке новых материалов с необычными свойствами и потенциальными применениями в квантовых технологиях, позволяя перейти от эмпирического поиска к предсказуемому конструированию материалов с заданными топологическими характеристиками.

Предложенный теоретический каркас открывает перспективные пути для обнаружения и использования материалов, демонстрирующих дробные возбуждения, подобно тем, что наблюдаются в дробных изоляторах Черна. Эти материалы характеризуются необычными электронными свойствами, где электроны «расщепляются» на квазичастицы с дробным зарядом и статистикой, что приводит к возникновению новых фаз материи и потенциально революционным технологическим приложениям. Исследования в этой области направлены на поиск материалов с определенной топологической структурой, способной поддерживать и контролировать эти дробные возбуждения, что может привести к созданию более эффективных и надежных электронных устройств, а также к развитию квантовых вычислений и других передовых технологий. Понимание механизмов возникновения и управления дробными возбуждениями позволит создавать материалы с принципиально новыми функциональными возможностями.

Исследование, представленное в данной работе, демонстрирует, что робастность топологических свойств материалов возникает не из централизованного управления, а из локальных взаимодействий, отраженных в спектроскопических интенсивностях. Авторы предлагают метод, позволяющий напрямую измерять эти свойства через ‘фактор формы волновой функции’, что подчеркивает превалирование структуры системы над попытками внешнего контроля. В этом контексте, слова Людвига Витгенштейна особенно актуальны: «Грань нашей языковой компетенции означает грань нашего мира». Подобно тому, как наше понимание мира ограничено языком, так и наше понимание топологических свойств материала ограничено методами его исследования. Способность измерять ‘кривизну Берри’ и другие геометрические характеристики через спектроскопию расширяет эту компетенцию, открывая новые грани понимания.

Куда же дальше?

Представленный подход, измеряющий топологию и геометрию через интенсивности спектров, открывает, скорее, возможности для постановки новых вопросов, чем даёт окончательные ответы. Стремление к определению глобальных топологических инвариантов через локальные измерения — занятие, конечно, заманчивое, но иллюзорное. В сложных системах порядок не нуждается в архитекторе — он возникает из локальных правил, и попытки навязать сверху иерархию лишь создают артефакты. Поэтому, наиболее перспективным представляется не поиск универсальных индикаторов, а детальное изучение того, как локальные свойства волновых функций определяют наблюдаемые спектроскопические характеристики.

Ограничения метода, связанные с разрешением и точностью измерений, очевидны. Однако, более принципиальным является вопрос о применимости данного подхода к сильнокоррелированным системам, где понятие квазичастицы становится размытым. Возможно, необходимо будет разработать новые теоретические инструменты, учитывающие коллективные возбуждения и взаимодействия, чтобы извлекать информацию о топологии и геометрии из спектральных данных. Контроль — иллюзия, влияние — реально; задача исследователя — не управлять системой, а стимулировать её внутренние правила.

В конечном счете, системный результат непредсказуем, но устойчив. Вместо того, чтобы стремиться к абсолютному пониманию, следует сосредоточиться на создании моделей, способных предсказывать наблюдаемые явления в определённом диапазоне параметров. Перспективы лежат в разработке вычислительных алгоритмов, позволяющих эффективно анализировать большие объёмы спектроскопических данных и выявлять закономерности, скрытые в шуме.

Оригинал статьи: https://arxiv.org/pdf/2601.10677.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-16 12:18