Геометрия Рассуждений: Скрытые Пространства Математических Теорий

Автор: Денис Аветисян

---

В статье исследуется возможность визуализации и анализа логических теорий через построение «скрытого пространства», объединяющего методы математической логики и машинного обучения.

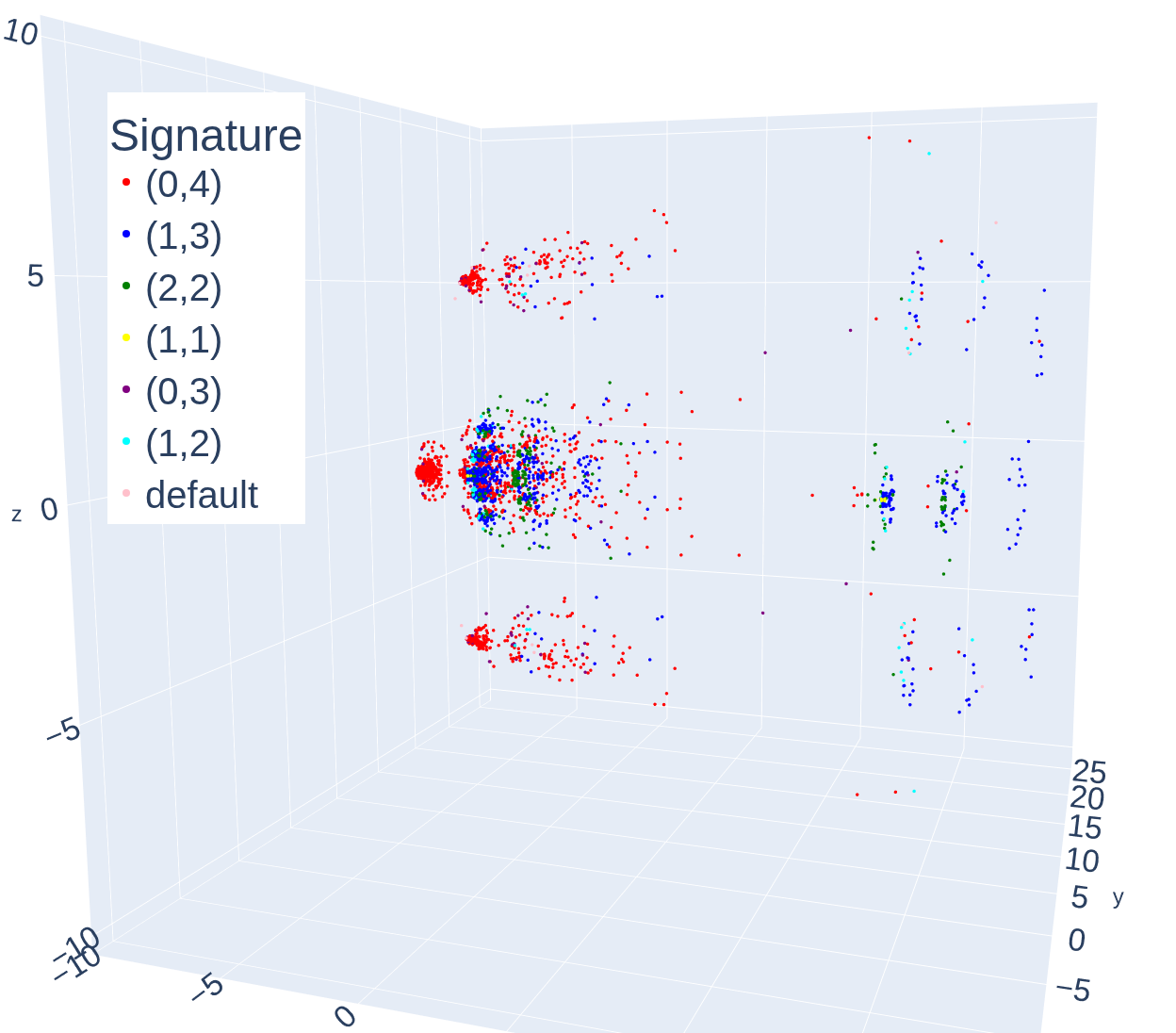
Исследование латентного пространства эквациональных теорий с использованием графов импликаций и методов, заимствованных из анализа главных компонент.

Несмотря на фундаментальную роль уравнений в математике, систематическое исследование пространства всех возможных уравнений и их взаимосвязей оставалось сложной задачей. В статье ‘The Latent Space of Equational Theories’ представлен новый подход к этой проблеме, основанный на объединении идей из конечной модельной теории и машинного обучения. Авторы конструируют латентное пространство для уравнений, определяемое статистическим поведением этих уравнений на конечных магмах, что позволяет впервые наблюдать геометрические структуры и потоки логических следствий в этом пространстве. Какие новые инсайты в структуру математической логики и алгебры могут быть получены благодаря дальнейшему исследованию этого латентного пространства и его связи с другими математическими объектами?

---

Основы: Ландшафт Эквациональных Теорий

Основой для широкого спектра алгебраических структур служит изучение магм — множеств, наделенных бинарными операциями. Магма представляет собой наиболее общую алгебраическую структуру, не требующую каких-либо специфических свойств операции, таких как ассоциативность или коммутативность. По сути, любая операция над множеством определяет магму, что делает этот подход фундаментальным для анализа различных алгебраических систем. Именно из магм, путем наложения дополнительных ограничений на бинарную операцию, возникают такие известные структуры, как полугруппы, моноиды, группы, кольца и поля. Таким образом, глубокое понимание свойств магм является ключевым для всестороннего изучения алгебры и ее многочисленных приложений.

Эквациональные теории представляют собой формальный аппарат для описания алгебраических структур, основанный на наборе уравнений, определяющих отношения между элементами и операциями в рассматриваемой структуре. Данный подход позволяет строго определить свойства и поведение различных алгебраических систем, таких как группы, кольца и поля, через логические следствия из заданных уравнений. Каждое уравнение, по сути, выражает тождество, которое должно выполняться для всех элементов структуры, обеспечивая тем самым согласованность и предсказуемость ее свойств. Использование эквациональных теорий позволяет не только классифицировать алгебраические структуры, но и выявлять общие закономерности и связи между ними, что является ключевым для развития современной алгебры и ее приложений.

Исчерпывающее картирование взаимосвязей между различными эквациональными теориями представляло собой сложную вычислительную задачу, требующую систематического подхода. Для ее решения был проведен анализ 4694 эквациональных теорий, что позволило установить иерархию и взаимосвязи между ними. Этот масштабный анализ потребовал разработки эффективных алгоритмов и значительных вычислительных ресурсов, поскольку каждая теория должна была быть проверена на совместимость и включение в другие теории. Полученные результаты не только углубляют понимание алгебраических структур, но и предоставляют основу для автоматизированной проверки и доказательства свойств, связанных с этими теориями, открывая новые возможности для исследований в области универсальной алгебры и смежных областях.

Установление Порядка: Преордер Импликаций

В рамках проекта «Equational Theories» был успешно построен порядок импликаций, определяющий взаимосвязи между 4694 эквациональными теориями. Этот результат представляет собой систематизированный набор данных, устанавливающий отношения подчиненности между различными теориями, где каждая теория либо следует из другой, либо не следует. Конструкция порядка импликаций потребовала обширного анализа и сравнения аксиоматических систем, что позволило создать полную и непротиворечивую структуру взаимосвязей между исследованными теориями.

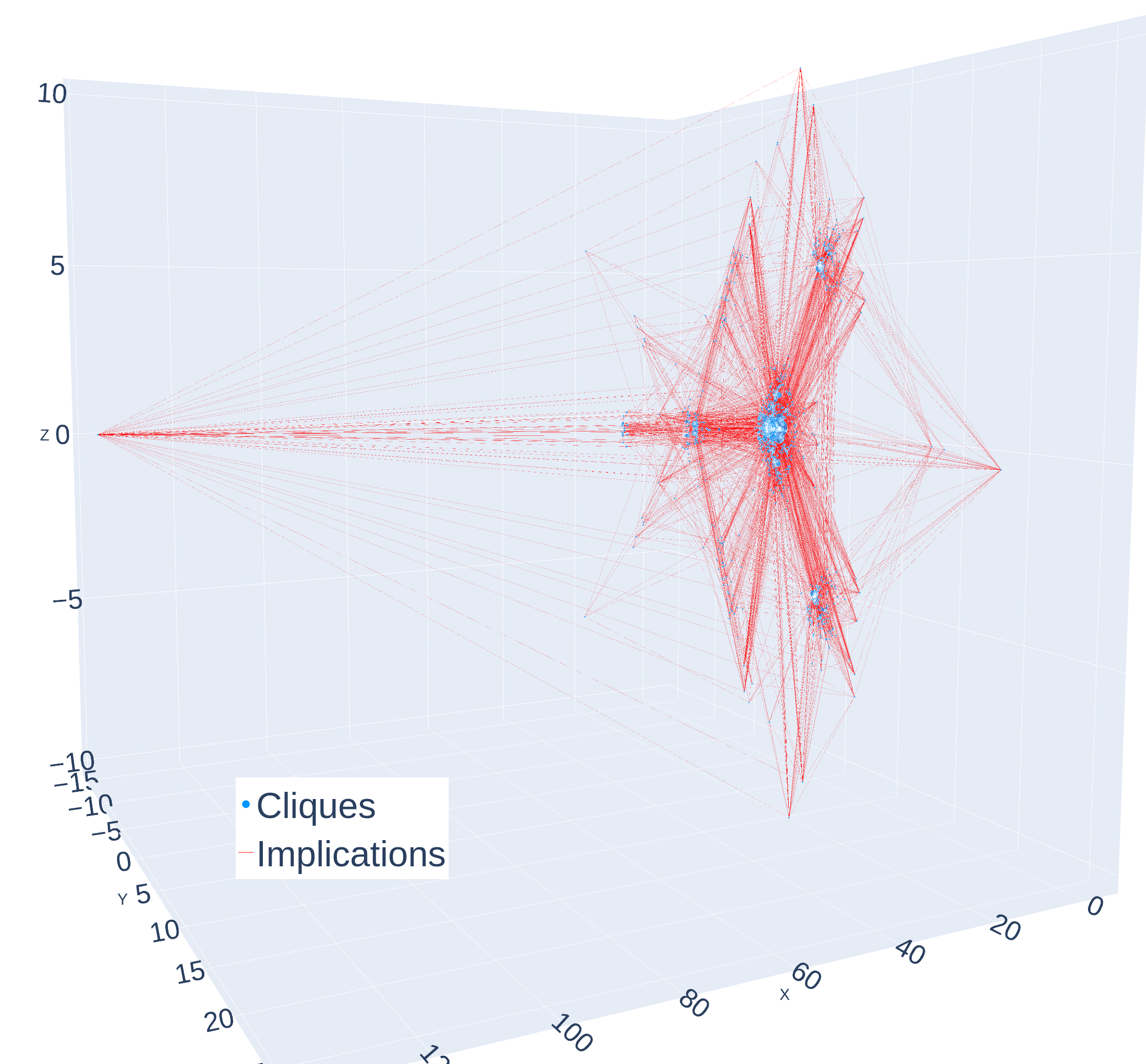
Предварительный порядок, построенный в рамках проекта Equational Theories, предоставляет базовый ресурс для изучения внутренней структуры пространства эквациональных теорий. Эта структура представлена графом импликаций, состоящим из 1415 вершин (с учетом обратимости). Каждая вершина соответствует определенной эквациональной теории, а ребра отражают отношения импликации между ними. Важно отметить, что количество вершин определено с учетом эквивалентности теорий по модулю обратимости, что позволяет избежать дублирования и упростить анализ.

Граф импликаций содержит 4824 ребра, учитывая упрощения и отношение обратимости. Каждое ребро представляет собой связь между двумя эквациональными теориями, указывая, что одна теория влечет другую после применения процедур упрощения. Важно отметить, что количество ребер при подсчете учитывает симметричные связи как отдельные, то есть отношение обратимости влияет на итоговое количество, но не изменяет базовое представление об отношениях импликации между теориями.

Вероятностный Взгляд: Пары Стоуна и Скрытые Пространства

Сопоставления Стоуна (Stone pairings) представляют собой вероятностный подход к оценке справедливости импликаций между эквациональными теориями. В рамках данной методики, каждая эквациональная теория сопоставляется с пространством вероятностей, где элементы этого пространства соответствуют различным моделям теории. Импликация между двумя теориями, T_1 и T_2, считается справедливой, если мера множества моделей, удовлетворяющих T_1, которые также удовлетворяют T_2, близка к единице. Использование вероятностных мер позволяет количественно оценить степень уверенности в справедливости импликации и учитывать неопределенность, связанную с бесконечным числом возможных моделей.

Применение Stone-пар сопоставлений позволяет определить пространство признаков (feature space) для эквациональных теорий, где каждая теория представляется как точка в этом пространстве. Ключевым является то, что, используя Stone-пар, можно сконструировать пространство скрытых признаков (Latent Space) меньшей размерности, сохраняя при этом важные характеристики исходных теорий. Это достигается за счет проецирования теорий из пространства признаков в пространство скрытых признаков, что позволяет эффективно представлять и анализировать сложные эквациональные системы, уменьшая вычислительную сложность и упрощая визуализацию.

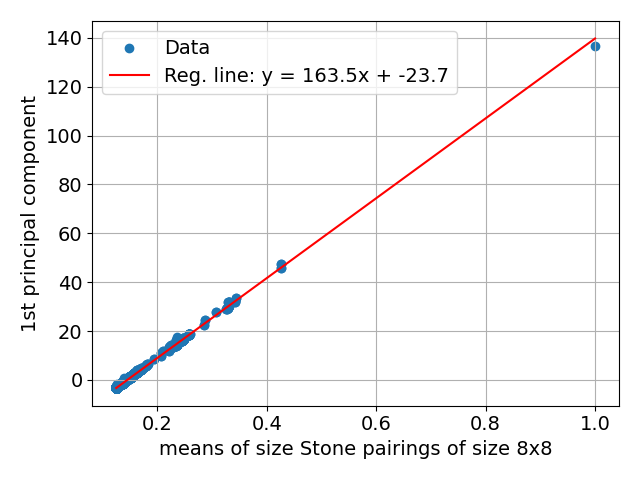
Применение метода главных компонент (Principal Component Analysis, PCA) к пространству скрытых представлений эквациональных теорий позволяет эффективно визуализировать и анализировать их структуру. PCA снижает размерность пространства, сохраняя при этом наиболее значимые компоненты, что облегчает обнаружение закономерностей. Экспериментальные данные показывают, что математически доказуемо эквивалентные теории формируют плотные кластеры в этом сниженном пространстве, что подтверждает эффективность использования Stone pairings для построения информативного представления об отношениях между теориями и позволяет проводить их сравнительный анализ.

Раскрытие Структуры: Характеристики и Инсайты

Латентное пространство эквациональных теорий характеризуется с помощью таких признаков, как математическое ожидание и дисперсия спариваний Стоуна, что позволяет получить количественные оценки сложности теории. Эти спаривания, по сути, отражают взаимосвязи между различными элементами теории, а их статистические характеристики — ожидание и разброс — служат мерой её структурной сложности. Теории с низким математическим ожиданием и низкой дисперсией спариваний демонстрируют более простую и упорядоченную структуру, в то время как высокие значения этих показателей свидетельствуют о большей сложности и непредсказуемости взаимосвязей. Таким образом, анализ спариваний Стоуна предоставляет мощный инструмент для количественной оценки и сравнения сложности различных эквациональных теорий, открывая новые возможности для их классификации и понимания.

Подпись эквациональной теории, представляющая собой количественную меру сложности уравнений, позволяет существенно уточнить наше понимание структуры и взаимосвязей между различными теориями. Исследование показывает, что анализ этой подписи выявляет тонкие различия в сложности уравнений, что, в свою очередь, дает возможность более детально картировать «ландшафт» эквациональных теорий. Определение сложности через подпись способствует выявлению закономерностей и классификации теорий по степени их сложности, открывая перспективы для разработки более эффективных алгоритмов и методов анализа в данной области. Использование данной метрики позволяет не только оценить сложность конкретной теории, но и сравнить различные теории между собой, выявляя общие черты и уникальные особенности.

В рамках изучения порядка импликации, ключевую роль играют понятия атомной и обратимой импликации, позволяющие детализировать взаимосвязи внутри данной структуры. Исследования показали, что средняя длина ребра, соответствующего обратимой импликации, составляет всего 0.69, что значительно меньше, чем для атомных (5.29) и строгих (7.17) импликаций. Эта разница в длине указывает на более тесную и непосредственную связь между элементами, соединенными обратимой импликацией, в отличие от более сложных и опосредованных связей, характерных для других типов импликаций. Таким образом, анализ длины ребер в порядке импликации предоставляет ценную информацию о природе и силе отношений между элементами в исследуемой теории.

Исследование, представленное в статье, демонстрирует стремление к выявлению скрытых структур в, казалось бы, абстрактных математических теориях. Построение латентного пространства для уравнений, с использованием методов конечной модельной теории и машинного обучения, раскрывает геометрические и статистические закономерности в процессах логического вывода. В этом контексте, слова Дональда Дэвиса представляются особенно уместными: «Простота — высшая форма изысканности». Эта фраза отражает суть работы — стремление к выявлению фундаментальных принципов, лежащих в основе сложной системы логических взаимосвязей, и представлению их в наиболее лаконичной и понятной форме. Акцент делается на выявлении главных компонентов, определяющих структуру теории, что соответствует стремлению к максимальной ясности и устранению избыточности.

Куда же дальше?

Представленная работа, стремясь к сжатию без потерь в пространстве эквациональных теорий, неизбежно обнажила области, где простота еще не достигнута. Построение латентного пространства — это, по сути, попытка отобразить сложность рассуждений в более управляемый геометрический объект. Однако, подобно любой карте, это лишь приближение. Необходимо критически оценить, насколько адекватно текущие методы, опирающиеся на конечную теорию моделей и методы машинного обучения, отражают истинную структуру этих пространств, особенно для теорий, выходящих за рамки конечности.

Особое внимание следует уделить вопросам масштабируемости. При увеличении сложности эквациональных теорий, вычислительные затраты на построение латентного пространства растут экспоненциально. Поиск более эффективных алгоритмов, возможно, основанных на альтернативных подходах к снижению размерности или на приближенных методах, представляется ключевой задачей. Вместе с тем, важно помнить, что любое упрощение несет в себе риск потери информации.

В конечном итоге, ценность представленного подхода заключается не столько в получении конкретных результатов, сколько в постановке вопроса о внутренней геометрии рассуждений. Вполне вероятно, что глубокое понимание этой геометрии позволит создать более эффективные алгоритмы логического вывода, а также пролить свет на фундаментальные вопросы о природе математического знания. Но, как всегда, истина спрятана в деталях, а детали — в избыточности.

---

Оригинал статьи: https://arxiv.org/pdf/2601.20759.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

• Решение головоломки с паролем Absolum в Yeldrim.

• Шоу 911: Кто такой Рико Прием? Объяснение трибьюта Grip

• Все рецепты культистского круга в Escape from Tarkov

• Лучшие шаблоны дивизий в Hearts Of Iron 4

• Лучшие транспортные средства в Far Cry 6

• Необходимо: Как выращивать урожай

• All Valley Pass Aurylene Locations In Endfield

• В ролях: приглашенные звезды и актеры 22-го сезона 3-й серии «Морской полиции» (фотографии) – Донна Миллс в беде с Хэлом

• Палия: где найти сердечную лилию

• Нечестивцам нет покоя: как получить старый ключ от коттеджа

2026-01-29 13:29