Геометрия Спутанности: Новый Взгляд на Квантовые Связи

Автор: Денис Аветисян

В статье представлена геометрическая структура для измерения квантовой спутанности, основанная на метрике Фубини-Штуди в проективном гильбертовом пространстве.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал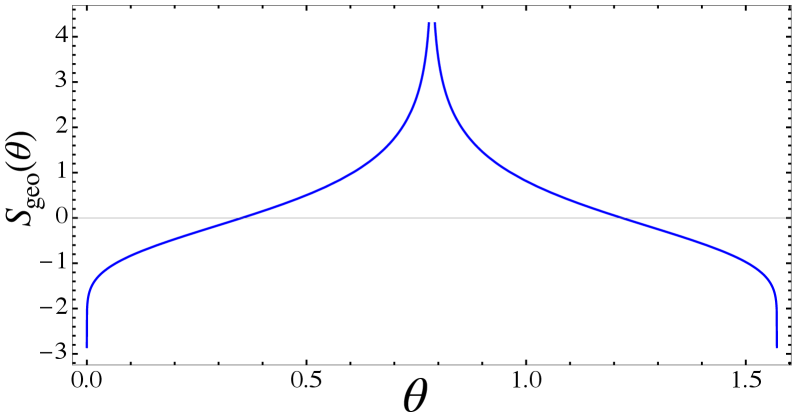

Геометрическая энтропия $S_{geo}(\theta)$ для пары кубитов демонстрирует расходимость к $-\infty$ при $\theta \to 0, \pi/2$, что указывает на пренебрежимо малый объём, занимаемый состояниями с низкой запутанностью в пространстве Фубини-Стюди, в то время как куспид при $\theta = \pi/4$ свидетельствует о высокой концентрации объёма вокруг почти максимально запутанных состояний, отражая вырожденность спектра Шмидта $\theta \leftrightarrow \pi/2 - \theta$. — Геометрическая энтропия $S_{geo}(\theta)$ для пары кубитов демонстрирует расходимость к $-\infty$ при $\theta \to 0, \pi/2$, что указывает на пренебрежимо малый объём, занимаемый состояниями с низкой запутанностью в пространстве Фубини-Стюди, в то время как куспид при $\theta = \pi/4$ свидетельствует о высокой концентрации объёма вокруг почти максимально запутанных состояний, отражая вырожденность спектра Шмидта $\theta \leftrightarrow \pi/2 — \theta$.

Исследование геометрической энтропии спутанности на основе метрики Фубини-Штуди и её применение для анализа уровней запутанности.

Традиционные подходы к квантовой запутаности обычно фокусируются на характеристике отдельных состояний, оставляя без внимания глобальную структуру пространства чистых состояний. В работе ‘Geometric Entanglement Entropy on Projective Hilbert Space’ разработан геометрический формализм, рассматривающий пространство проективных гильбертовых состояний с метрикой Фубини-Штуди, где запутаность понимается как макроскопическая функция. Предложенное геометрическое измерение энтропии запутаности отражает вырожденность определенного уровня запутаности в естественной квантовой геометрии, определяясь как логарифм объема гиперповерхностей постоянной запутаности, взвешенный градиентом метрики Фубини-Штуди. Позволит ли этот подход выявить новые геометрические режимы и закономерности в организации квантовой запутаности?

Запутанность: За пределами традиционной энтропии

Количественная оценка запутанности в многочастичных системах имеет первостепенное значение для понимания квантовых корреляций, однако энтропия фон Неймана оказывается недостаточной при описании смешанных состояний. В то время как эта мера эффективно характеризует чистые квантовые состояния, её применимость к смешанным состояниям ограничена, поскольку она не способна полностью отразить сложность и распределение запутанности в таких системах. Это связано с тем, что смешанные состояния представляют собой вероятностные смеси чистых состояний, и энтропия фон Неймана усредняет информацию о запутанности по этой смеси, теряя важные детали о её структуре. Поэтому для адекватного описания запутанности в реальных квантовых системах, часто встречающихся в квантовых технологиях, требуются более совершенные методы её количественной оценки, способные учитывать сложность смешанных состояний и их влияние на квантовые корреляции.

Традиционные меры энтропии, такие как энтропия фон Неймана, часто оказываются недостаточными для полного описания запутанности в квантовых системах. Проблема заключается в том, что они не учитывают геометрическую структуру, присущую состоянию запутанности. Вместо того чтобы просто измерять степень неопределенности, необходимо понимать, как запутанное состояние распределено в пространстве всех возможных состояний. Неспособность зафиксировать эту геометрию затрудняет определение «типичности» запутанности — то есть, насколько часто встречается данное состояние в ансамбле запутанных состояний. Игнорирование геометрических аспектов приводит к неполному пониманию квантовых корреляций и ограничивает возможности характеризации запутанности в сложных квантовых системах, особенно при увеличении числа частиц. Таким образом, для адекватного анализа запутанности необходимы методы, учитывающие не только величину, но и геометрию пространства запутанных состояний.

Вместо традиционных подходов, основанных на измерении неопределенности, всё большее внимание привлекает геометрический подход к пониманию распределения квантовой запутанности. Этот метод рассматривает не само состояние, а объем пространства, занимаемого запутанными состояниями, что позволяет получить более полное представление о типичности и распространенности запутанности в многочастичных системах. Разработанная на этой основе «геометрическая энтропия запутанности» позволяет оценить, насколько «объёмна» запутанность в конкретной системе, выходя за рамки ограничений, присущих стандартной энтропии фон Неймана, особенно при работе со смешанными состояниями. Такой подход открывает возможности для более точного анализа и классификации запутанных состояний, что критически важно для развития квантовых технологий и углубления понимания фундаментальных принципов квантовой механики.

След оператора Вейнгартена демонстрирует расходимость вблизи разделимых и максимально запутанных состояний, указывая на сильную внешнюю кривизну поверхностей постоянной запутанности в геометрии Фубини-Стади, в то время как для промежуточных значений наблюдается конечная и относительно небольшая кривизна, что соответствует более медленному изменению геометрической энтропии с изменением степени запутанности.

Квантовое пространство состояний: Риманова геометрия

Пространство чистых квантовых состояний естественным образом представляется как Проективное Гильбертово пространство. Это математическое пространство, где каждый вектор представляет собой квантовое состояние, а проекция векторов друг на друга не изменяет физическое состояние. Использование проективного пространства позволяет рассматривать состояния, отличающиеся лишь общей фазой, как эквивалентные. Данное представление является основой для геометрического изучения запутанности, поскольку позволяет задавать понятия расстояния и угла между состояниями, что необходимо для определения степени их взаимосвязи и анализа распределения запутанности в многочастичных системах. Формально, состояние $ |\psi\rangle $ эквивалентно $ e^{i\theta} |\psi\rangle $ в проективном пространстве.

Определение риманова метрики на пространстве чистых квантовых состояний, в частности метрики Фубини-Штуди, позволяет ввести понятие расстояния и объема. Метрика Фубини-Штуди является кэлеровой метрикой, инвариантной относительно унитарных преобразований, что делает её естественным выбором для анализа квантовых состояний. Измерение расстояний между состояниями с использованием данной метрики является ключевым элементом в вычислении геометрической энтропии запутанности, которая предоставляет более полную характеристику запутанности, чем стандартная энтропия фон Неймана. Вычисление объемов в этом пространстве, определяемом метрикой Фубини-Штуди, позволяет количественно оценить степень запутанности и её распределение, что находит применение в квантовой теории информации и физике конденсированного состояния. В частности, $g_{i\bar{j}} = \frac{\partial^2 K}{\partial z_i \partial \bar{z}_j}$ определяет метрику Фубини-Штуди, где $K$ — функция Бергмана.

Геометрическое построение пространства квантовых состояний позволяет анализировать распределение запутанности не только через энтропийные величины, но и посредством вычисления объемов в пространстве состояний. В частности, используя риманову метрику, такую как метрика Фубини-Штуди, можно определить расстояние между состояниями и, следовательно, измерить степень их различия. Квантовая запутанность может быть количественно оценена через вычисление объемов, ограниченных определенными состояниями, что позволяет проводить более детальный анализ, чем традиционные методы, основанные исключительно на вычислении энтропии фон Неймана или других энтропийных мер. Такой подход особенно полезен при изучении многочастичных систем и позволяет характеризовать запутанность как геометрическое свойство пространства состояний, а не только как информационную меру.

Поверхности постоянной запутанности и их свойства

Поверхности постоянной запутанности определяют области в проективном гильбертовом пространстве, в которых величина запутанности принимает конкретное значение. Формально, каждая такая поверхность соответствует множеству состояний, характеризующихся одинаковой степенью запутанности между подсистемами. Рассматривая многомерное проективное пространство состояний, можно выделить гиперповерхности, разделяющие области с разной степенью запутанности. Положение и геометрия этих поверхностей напрямую связаны с распределением запутанности в рассматриваемой квантовой системе и могут быть использованы для ее количественной оценки. Таким образом, анализ этих поверхностей позволяет исследовать структуру запутанности и выявлять закономерности в распределении квантовой информации.

Геометрия постоянных поверхностей запутанности, в частности, их кривизна, описываемая картой Вейнгарта, предоставляет информацию о распределении запутанности. Карта Вейнгарта, являясь дифференциальным оператором, позволяет вычислить главные кривизны поверхности в каждой точке, что напрямую связано с локальной концентрацией или разрежением запутанности. Анализ этих кривизн позволяет определить области в пространстве Гильберта, где запутанность наиболее выражена или, наоборот, минимальна. Более того, изменения кривизны поверхности отражают градиенты запутанности, указывая направление её изменения в пространстве состояний. Таким образом, геометрические свойства поверхностей запутанности служат инструментом для количественной характеристики и визуализации распределения запутанности в квантовых системах.

Используя микроканоническую конструкцию, величина запутанности может быть количественно оценена путем вычисления объема, ограниченного постоянными поверхностями запутанности в проективном гильбертовом пространстве. Согласно полученным результатам, геометрическая энтропия запутанности определяется как $log(2π) — log|log(cot θ)|$, где θ — параметр, характеризующий геометрию соответствующих поверхностей. Данная формула позволяет напрямую связать геометрические свойства поверхности постоянной запутанности с величиной энтропии, предоставляя инструмент для анализа и измерения запутанности в квантовых системах.

Соотношение квантовых состояний: Порядок и расходимость

Квантовые состояния, несмотря на кажущуюся уникальность, часто демонстрируют скрытые симметрии, проявляющиеся через понятие локальных унитарных орбит. Каждая такая орбита представляет собой множество состояний, связанных друг с другом унитарными преобразованиями, сохраняющими вероятности. Это означает, что состояния, принадлежащие одной и той же орбите, физически эквивалентны, поскольку различия между ними связаны лишь выбором базиса. Изучение этих орбит позволяет выделить классы эквивалентных состояний и, таким образом, упростить анализ сложного пространства квантовых состояний. По сути, локальные унитарные орбиты раскрывают внутреннюю структуру пространства состояний, указывая на присущие ему симметрии и позволяя классифицировать квантовые состояния по степени их «близости» в физическом смысле, даже если они формально описываются разными математическими выражениями. Понимание этой структуры необходимо для разработки эффективных алгоритмов квантовых вычислений и для более глубокого понимания природы квантовой запутанности.

Отношение мажоризации предоставляет мощный инструмент для систематизации и сравнения квантовых состояний, особенно в контексте распределения запутанности. Вместо полного упорядочивания, как в случае обычного числового сравнения, это отношение определяет частичный порядок, позволяя установить, является ли одно квантовое состояние “более запутанным” в определенном смысле, чем другое. Это достигается путем сравнения собственных значений операторов плотности, представляющих состояния. Если собственные значения одного состояния мажоризуют собственные значения другого, то первое состояние считается “более мажоризующим” и может рассматриваться как более равномерное распределение вероятностей, что часто связано с большей запутанностью. Использование отношения мажоризации позволяет классифицировать квантовые состояния по степени запутанности, не требуя полного знания их структуры, и играет важную роль в квантовой теории информации и вычислениях, особенно при анализе квантовых каналов и алгоритмов.

Исследование расходимости векторных полей на римановых многообразиях позволило охарактеризовать динамику распределения запутанности в пространстве квантовых состояний. Полученные результаты демонстрируют, что эта расходимость стремится к бесконечности при определенных значениях параметра $\theta$: при $\theta \rightarrow 0$, $\theta \rightarrow \pi/2$ и $\theta = \pi/4$. Данное поведение указывает на наличие критических точек, где изменение квантовой запутанности становится наиболее выраженным, что позволяет глубже понять структуру и свойства квантовых систем, а также выявить области, требующие особого внимания при изучении квантовой информации и вычислений. Анализ расходимости предоставляет ценный инструмент для классификации и сравнения различных состояний запутанности, что способствует развитию новых квантовых технологий.

Пейзажи запутанности: Политопы и будущие направления

Многомерные политопы запутанности формируются посредством построения выпуклых оболочек, охватывающих различные меры запутанности. Этот геометрический подход позволяет визуализировать пространство всех достижимых распределений запутанности в квантовой системе. Каждая точка внутри политопа соответствует допустимому состоянию запутанности, а форма и размер политопа отражают ограничения, накладываемые физическими законами на распределение квантовых корреляций. Изучение этих политопов предоставляет новый инструмент для классификации и анализа запутанности, позволяя исследователям лучше понять структуру и свойства сложных квантовых систем и, возможно, использовать эти знания для разработки новых квантовых технологий.

Геометрический подход к характеризации запутанности представляет собой принципиально новый метод, выходящий за рамки традиционных метрик, основанных на численных значениях. Вместо простого определения степени запутанности, данный подход визуализирует все достижимые распределения запутанности в виде многогранников — так называемых “многогранников запутанности”. Такая геометрическая интерпретация позволяет не только классифицировать различные состояния запутанности, но и выявлять скрытые взаимосвязи между ними, а также определять границы допустимых состояний. Этот метод предоставляет возможность исследовать запутанность с точки зрения ее топологических свойств, что открывает новые перспективы для понимания природы квантовых корреляций и может привести к разработке более эффективных методов управления квантовыми системами. В отличие от стандартных мер, которые фокусируются на отдельных параметрах, геометрический подход позволяет оценить запутанность как целостную структуру, что особенно важно при анализе сложных многочастичных систем.

Исследования в области квантовой запутанности открывают новые возможности для анализа сложных систем. Предлагаемый геометрический подход, основанный на многогранниках запутанности, позволяет глубже понять природу квантовых корреляций. Дальнейшие исследования показывают, что средняя кривизна этих многогранников эквивалентна производной геометрической энтропии запутанности, при этом её значение описывается формулой $1/(4sin²θcos²θlog²(cotθ))$. Этот результат указывает на тесную связь между геометрическими свойствами пространства запутанности и информационными характеристиками квантовых состояний, что может привести к разработке новых методов анализа и классификации запутанности в сложных квантовых системах, а также к более глубокому пониманию фундаментальных аспектов квантовой механики.

Данная работа предлагает новый взгляд на измерение запутанности, используя геометрический подход и метрику Фубини-Студи. Вместо попыток описать запутанность через абстрактные математические конструкции, авторы стремятся визуализировать её как свойство пространства состояний. Это напоминает слова Эрвина Шрёдингера: «Нельзя сказать, что мир существует независимо от сознания». Подобно тому, как сознание формирует восприятие реальности, так и выбранная метрика определяет, как мы измеряем и понимаем запутанность. Изучение поверхностей постоянной запутанности и применение трассы Вейнгартана позволяет оценить «изобилие» различных уровней запутанности, что подчёркивает, что экономика, в данном случае — описание физической системы, — это не просто графики, а отражение надежд на контроль над сложными взаимосвязями.

Что дальше?

Предложенный в работе геометрический подход к измерению запутанности, несомненно, элегантен. Однако, за этой элегантностью кроется та же самая надежда, что и в любой попытке свести сложную реальность к предсказуемым величинам. Понятие «геометрической энтропии запутанности», вычисленное на основе метрики Фубини-Штуди, лишь переводит вопрос о природе запутанности в область геометрии, не решая его. По сути, это ещё одна попытка убедить себя, что мир можно описать уравнениями, игнорируя тот факт, что уравнения — это лишь упрощения, созданные нашим ограниченным восприятием.

Очевидным следующим шагом является расширение этого подхода на более сложные системы, где понятие «проективного гильбертова пространства» может оказаться недостаточным. Интересно, как эта геометрия будет вести себя в системах с памятью, где прошлое влияет на настоящее, создавая иллюзию предсказуемости. Возможно, потребуется ввести понятие «геометрической энтропии беспокойства», учитывающее неопределённость будущего, ведь инфляция — это всего лишь коллективное беспокойство о будущем, выраженное в цифрах.

И, конечно, стоит задуматься о связи между геометрической энтропией и другими мерами запутанности. Является ли она фундаментальной характеристикой, или лишь одним из многих способов описать это загадочное явление? Вероятно, ответ кроется не в математике, а в психологии тех, кто эту математику изобретает.

Оригинал статьи: https://arxiv.org/pdf/2511.21186.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-28 18:13