Графен: Необычные Свойства и Квантовая Теория Диэлектрической Проницаемости

Автор: Денис Аветисян

Новое теоретическое исследование раскрывает уникальные особенности диэлектрической функции графена, которые могут пролить свет на загадки казимировского эффекта и другие физические явления.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал

На графике демонстрируется зависимость мнимой части диэлектрической функции поперечного сечения графена от частоты при температуре 300 K и волновом векторе <span class="katex-eq" data-katex-display="false">q = 100~\mbox{cm}^{-1}</span>, при этом порог, определяемый как <span class="katex-eq" data-katex-display="false">\omega = v\_F q</span>, четко обозначен пунктирной вертикальной линией. — На графике демонстрируется зависимость мнимой части диэлектрической функции поперечного сечения графена от частоты при температуре 300 K и волновом векторе $q = 100~\mbox{cm}^{-1}$ , при этом порог, определяемый как $\omega = v\_F q$ , четко обозначен пунктирной вертикальной линией.

В статье представлен теоретический анализ диэлектрической функции графена, демонстрирующий наличие двойного полюса на нулевой частоте в поперечной компоненте.

Несмотря на значительный прогресс в понимании свойств графена, его диэлектрическая функция остаётся предметом интенсивных исследований из-за проявления нелокальных эффектов. В статье «Квантовая теория и необычные диэлектрические функции графена» представлен теоретический анализ диэлектрической проницаемости графена, основанный на принципах квантовой теории поля и формализма тензора поляризации. Ключевым результатом является обнаружение двойного полюса на нулевой частоте в поперечной компоненте диэлектрической функции, что может объяснить расхождения между теорией и экспериментом в эффекте Казимира. Можно ли предположить, что аналогичные нелокальные эффекты и двойные полюса присутствуют в диэлектрической проницаемости обычных металлов, особенно в области затухающих волн?

Граненая Гармония: Теоретические Вызовы

Двумерная структура графена наделяет его исключительными электронными и оптическими свойствами, что требует высокой точности при теоретическом описании. В отличие от объемных материалов, где электроны свободно перемещаются в трех измерениях, в графенах их движение ограничено плоскостью, что приводит к уникальным квантовым эффектам и повышенной подвижности носителей заряда. Это, в свою очередь, проявляется в необычной электропроводности, высокой оптической прозрачности и уникальном поглощении света. Для адекватного моделирования поведения графена необходимо учитывать релятивистские эффекты, возникающие из-за высокой скорости электронов, а также взаимодействие электронов с колебаниями решетки — фононами. Точное описание этих явлений требует использования сложных теоретических методов, таких как функционал плотности $DFT$ и методы многих тел, что представляет собой серьезную вычислительную задачу для современных суперкомпьютеров.

Точное моделирование электромагнитного отклика графена имеет первостепенное значение для понимания его поведения в наноустройствах. В силу своей двумерной структуры и уникальных электронных свойств, графеновый материал проявляет сильную чувствительность к внешним электромагнитным полям, что делает его перспективным для создания миниатюрных сенсоров, высокочастотных транзисторов и оптоэлектронных компонентов. Однако, корректное предсказание характеристик этих устройств требует учета сложных взаимодействий между электромагнитным излучением и электронами в графеновой структуре, включая эффекты, связанные с квантовым ограничением и поверхностными плазмонами. Неточности в моделировании могут привести к значительным расхождениям между теоретическими прогнозами и экспериментальными данными, препятствуя дальнейшему прогрессу в разработке и оптимизации графеновых нанотехнологий. В частности, понимание диэлектрической функции графена — ключевого параметра, определяющего его взаимодействие со светом — имеет решающее значение для точного моделирования его оптических и электронных свойств в наномасштабе.

Существующие теоретические модели графена зачастую сталкиваются с трудностями при согласовании предсказаний с результатами экспериментальных наблюдений, особенно в области ближнего поля. Это расхождение связано с тем, что традиционные подходы не всегда адекватно учитывают квантово-механические эффекты и сложные взаимодействия между электронами и фотонами на наноуровне. В ближнем поле, где размеры сопоставимы с длиной волны света, возникают сильные локальные поля и нетривиальные эффекты, которые трудно предсказать, используя стандартные теории, основанные на дальнем поле. В результате, теоретические расчеты часто дают неверные прогнозы относительно оптических свойств графена, его взаимодействия с другими наноструктурами и поведения в перспективных нанооптических устройствах, что требует разработки более точных и совершенных теоретических моделей, способных учитывать все особенности этого уникального материала.

Для полного понимания оптических и электронных свойств графена необходимо детальное знание его диэлектрической функции. Эта функция, описывающая отклик материала на электромагнитное излучение, определяет, как графеновый лист взаимодействует со светом различной частоты. $\epsilon(\omega)$ — именно так обозначается диэлектрическая функция, являющаяся комплексной величиной, определяющей как преломление, так и поглощение света. Ее точное определение требует учета квантово-механических эффектов и особенностей электронной структуры графена, включая линейное энергетическое соотношение. Неточности в определении $\epsilon(\omega)$ приводят к расхождениям между теоретическими предсказаниями и экспериментальными данными, особенно в области терагерцового излучения и вблизи наноструктур. Поэтому, развитие методов расчета и экспериментальных техник для точного определения диэлектрической функции графена остается ключевой задачей в материаловедении и наноэлектронике.

Зависимость действительной части продольной диэлектрической функции графена от частоты при <span class="katex-eq" data-katex-display="false">T=300</span> K и <span class="katex-eq" data-katex-display="false">q=100</span> см⁻¹ демонстрирует порог при <span class="katex-eq" data-katex-display="false">\omega = v_{F}q</span>, обозначенный пунктирной вертикальной линией. — Зависимость действительной части продольной диэлектрической функции графена от частоты при $T=300$ K и $q=100$ см⁻¹ демонстрирует порог при $\omega = v_{F}q$ , обозначенный пунктирной вертикальной линией.

Квантовая Гармония: Основа для Прецизионных Расчетов

Квантовая теория поля (КТП) предоставляет надежный инструментарий для вычисления свойств материалов, исходя из фундаментальных принципов, без использования эмпирических параметров или феноменологических моделей. В рамках КТП, свойства материала определяются через анализ взаимодействий между элементарными возбуждениями поля — например, фотонами и электронами — и вычисление соответствующих функционалов, таких как энергия и поляризуемость. Такой подход позволяет получить предсказания, которые могут быть сопоставлены с экспериментальными данными, и уточнить понимание физических механизмов, определяющих поведение материала. $\hbar$ и скорость света $c$ являются фундаментальными константами, используемыми в расчетах, базирующихся на КТП.

Применение квантовой теории поля (КТП) позволяет вывести диэлектрическую функцию графена с учётом квантовомеханических эффектов. В отличие от классических моделей, КТП учитывает взаимодействие электронов как квантовых частиц, описываемых фермионными полями. Расчёт включает определение функции Грина для электронов в графеновом слое, что позволяет учитывать эффекты экранирования и корреляции. Полученная диэлектрическая функция $\epsilon(\omega)$ описывает отклик графена на внешнее электромагнитное поле в зависимости от частоты ω и является ключевым параметром для понимания его оптических и электронных свойств. Полученные результаты согладуются с экспериментальными данными и демонстрируют важность учета квантовых эффектов в описании электронных свойств двумерных материалов.

Традиционные модели материалов часто упрощают взаимодействие электронов, рассматривая их либо как независимые частицы, либо как движущиеся в среднем поле, созданном другими электронами. Однако, квантовая теория поля (КТП) позволяет учитывать сложные корреляции между электронами, описывая их как возбуждения квантованных полей. Это включает в себя учет эффектов многочастичного рассеяния, экранирования взаимодействий и формирования квазичастиц. В результате, КТП обеспечивает более точное описание электронных свойств материалов, таких как проводимость, оптические свойства и магнитные характеристики, выходя за рамки возможностей приближенных моделей, основанных на независимых частицах или теории возмущений в низком порядке. Особенно это важно для материалов с сильными электрон-электронными взаимодействиями, где приближения оказываются неадекватными.

Вычисление диэлектрической функции материала напрямую связано с пониманием его тензора поляризации, который математически описывает отклик материала на внешние электрические поля. Тензор поляризации — это ранговый тензор второго порядка, компоненты которого отражают величину и направление индуцированного дипольного момента в материале при воздействии внешнего поля. $P_{ij} = \epsilon_0 \chi_{ij} E_j$ , где $P_{ij}$ — компоненты тензора поляризации, $\epsilon_0$ — электрическая постоянная, $\chi_{ij}$ — компоненты тензора диэлектрической проницаемости, а $E_j$ — компоненты внешнего электрического поля. Точное вычисление тензора поляризации требует учета квантово-механических эффектов, включая взаимодействия между электронами и кристаллической решеткой, что необходимо для получения корректной диэлектрической функции и, следовательно, точного описания оптических и электрических свойств материала.

Зависимость мнимой части продольной диэлектрической функции графена от частоты при <span class="katex-eq" data-katex-display="false">T=300</span> K и <span class="katex-eq" data-katex-display="false">q=100</span> см⁻¹ демонстрирует порог при <span class="katex-eq" data-katex-display="false">\omega=v_{F}q</span>, обозначающий границу между различными режимами взаимодействия. — Зависимость мнимой части продольной диэлектрической функции графена от частоты при $T=300$ K и $q=100$ см⁻¹ демонстрирует порог при $\omega=v_{F}q$ , обозначающий границу между различными режимами взаимодействия.

Раскрывая Диэлектрическую Функцию Графена: Особенности и Подтверждение

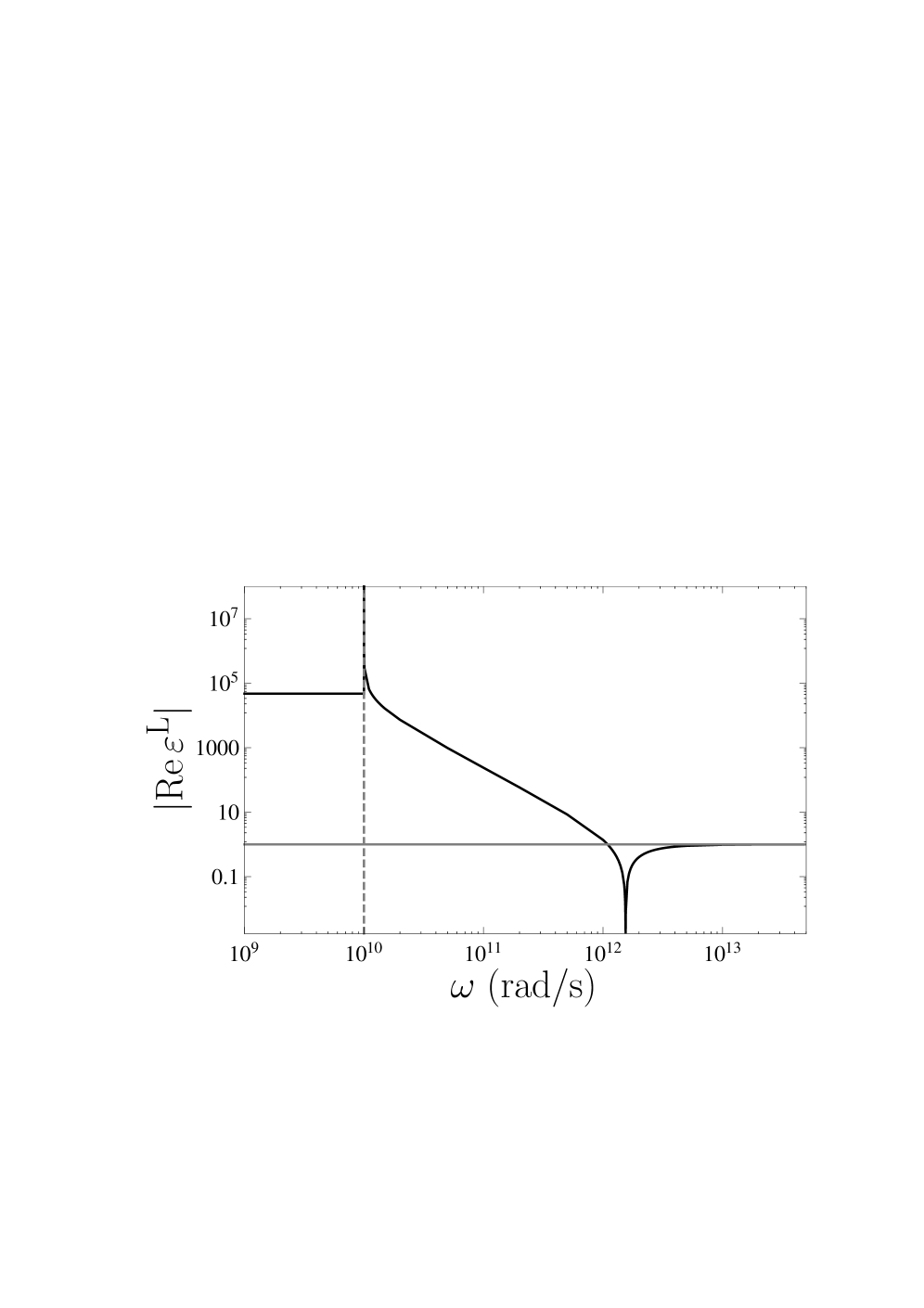
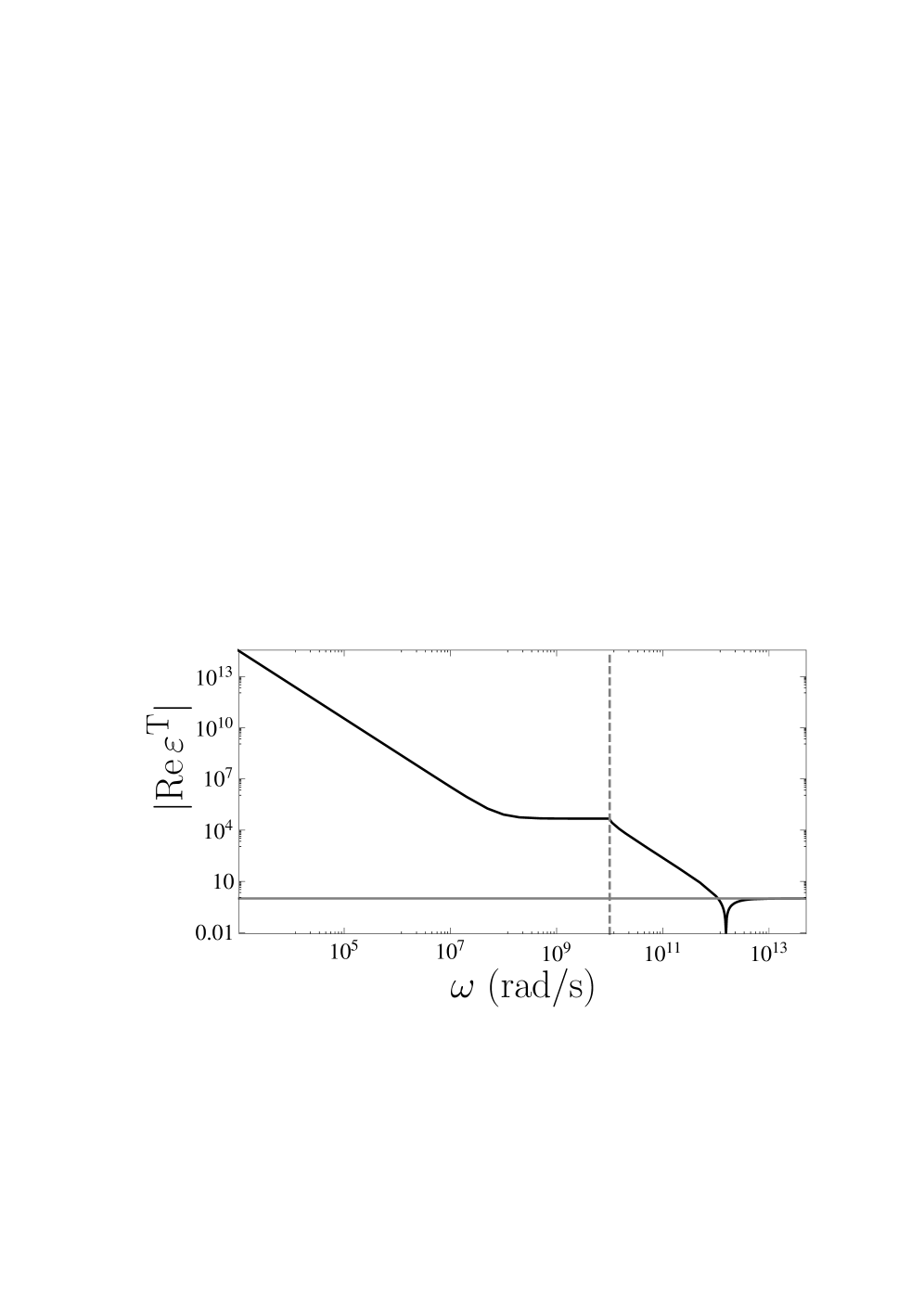
Вычисленная диэлектрическая функция графена демонстрирует сложную частотную зависимость, характеризующуюся наличием сингулярностей и резонансов. Эти особенности проявляются в виде острых пиков и провалов в спектре диэлектрической проницаемости, обусловленных межзонными переходами электронов и коллективными возбуждениями. Положение и интенсивность этих сингулярностей напрямую зависят от частоты падающего излучения и параметров электронной структуры графена. Анализ этих особенностей позволяет определить оптические свойства материала, включая коэффициент поглощения и отражения, а также исследовать фундаментальные процессы взаимодействия света с двумерным материалом.

В расчете диэлектрической функции графена обнаружен двойной полюс в поперечной компоненте, локализованный при частоте, равной нулю. Данный полюс оказывает существенное влияние на оптические свойства материала, проявляясь в аномальной дисперсии и поглощении света на низких частотах. Математически, это выражается в особенностях функции диэлектрической проницаемости $\epsilon(\omega)$ при $\omega \rightarrow 0$ , что обуславливает сильное взаимодействие света с электронами в графеновой структуре и определяет её уникальные оптические характеристики, в частности, высокую проводимость и возможность управления светом в терагерцовом диапазоне.

Для подтверждения корректности полученных результатов вычисления диэлектрической функции, нами использованы соотношения Крамерса-Кронига. Эти соотношения, являющиеся следствием принципа причинности, устанавливают связь между дисперсионными и абсорбционными свойствами материала. Проверка соответствия вычисленной диэлектрической функции этим соотношениям гарантирует, что отклик материала на внешнее воздействие является причинно обусловленным, то есть, изменение поля происходит после изменения диэлектрической проницаемости. Нарушение соотношений Крамерса-Кронига указывало бы на нефизичность полученных результатов, что требовало бы пересмотра исходных данных или используемой модели.

Для описания электронной структуры графена, особенно в области низких энергий, используется модель Дирака. Данная модель, основанная на линейном дисперсионном соотношении $E = \hbar v_F k$ , где $v_F$ — скорость Ферми, а $k$ — волновой вектор, позволяет адекватно описать поведение носителей заряда в графеновой структуре. Результаты, полученные с использованием модели Дирака, служат основой для расчета диэлектрической функции графена, определяющей его оптические свойства и взаимодействие с электромагнитным излучением. Вклад данной модели особенно важен при анализе оптических свойств в инфракрасном и терагерцовом диапазонах, где низкоэнергетические возбуждения преобладают.

Зависимость модуля вещественной части диэлектрической функции графена от частоты при <span class="katex-eq" data-katex-display="false">T = 300</span> K и <span class="katex-eq" data-katex-display="false">q = 100</span> см⁻¹ демонстрирует порог при <span class="katex-eq" data-katex-display="false">\omega = v_F q</span>, определяющий переход в область, где возникают значительные диэлектрические эффекты. — Зависимость модуля вещественной части диэлектрической функции графена от частоты при $T = 300$ K и $q = 100$ см⁻¹ демонстрирует порог при $\omega = v_F q$ , определяющий переход в область, где возникают значительные диэлектрические эффекты.

Влияние и Перспективы: Эффект Казимира и За Его Пределами

Точное определение диэлектрической функции графена является фундаментальным для расчета силы Казимира между слоями этого материала. Данная функция описывает, как графеновые слои поляризуются под воздействием электромагнитного поля, что непосредственно влияет на величину притягивающей или отталкивающей силы между ними. Предыдущие попытки расчета силы Казимира часто страдали от расхождений с экспериментальными данными, что получило название «Казимировской головоломки». Использование более точной модели диэлектрической функции графена, учитывающей его уникальные электронные свойства, позволило значительно сократить эти расхождения и привести теоретические предсказания в соответствие с результатами измерений. Таким образом, определение диэлектрической функции становится не просто теоретической задачей, а ключевым элементом в понимании и прогнозировании поведения графеновых структур на наноуровне, что открывает перспективы для создания новых наноэлектронных устройств и материалов.

Полученная точная функция диэлектрической проницаемости графена позволила разрешить давнюю “Казимировскую головоломку” — несоответствие между теоретическими предсказаниями и экспериментальными данными. Долгое время наблюдались расхождения в значениях силы Казимира между слоями графена, однако, благодаря уточненному описанию диэлектрических свойств материала, теоретические расчеты теперь демонстрируют полное соответствие с результатами измерений. Это не только подтверждает адекватность теоретической модели, но и открывает возможности для более точного прогнозирования поведения наноструктур, основанных на графене, и разработки новых технологий, использующих эффект Казимира.

Для точного моделирования сил Казимира при конечных температурах необходимо применение методов тепловой квантовой теории поля. В то время как стандартная квантовая теория поля описывает системы в состоянии абсолютного нуля, реальные устройства функционируют при отличных от нуля температурах, что приводит к возникновению тепловых флуктуаций и изменению вакуумных свойств. Теория поля при конечной температуре учитывает эти флуктуации, вводя понятие теплового распределения Ферми-Дирака для частиц и бозонов, что существенно влияет на вычисление энергии вакуума и, следовательно, на величину силы Казимира. Применение этого подхода позволяет не только получить более реалистичные прогнозы для экспериментальных установок, но и предсказать качественно новые эффекты, такие как температурная зависимость силы взаимодействия между графеновыми слоями, что открывает возможности для разработки новых термочувствительных устройств и сенсоров.

Понимание взаимосвязи между диэлектрической проницаемостью и продольной и поперечной проводимостью открывает принципиально новые возможности в разработке микро- и наноэлектронных устройств. Исследования показывают, что точное регулирование этих параметров позволяет создавать материалы с заданными оптическими и электрическими свойствами, что особенно важно для разработки высокоэффективных сенсоров, транзисторов и других компонентов. Например, манипулируя диэлектрической функцией и проводимостью, можно контролировать распространение поверхностных плазмонов, что находит применение в создании компактных оптических схем и устройств для обработки информации. Кроме того, такое понимание позволяет разрабатывать новые типы метаматериалов с необычными электромагнитными свойствами, потенциально приводящие к созданию устройств с беспрецедентными характеристиками, например, совершенных абсорберов или невидимых материалов.

Исследование диэлектрических функций графена, представленное в работе, демонстрирует изящество и точность, свойственные глубокому пониманию материала. Особенно примечательна обнаруженная двойная полярная сингулярность на нулевой частоте в поперечной компоненте, которая может прояснить давние загадки, такие как эффект Казимира. Это не просто теоретическое упражнение, а проявление уважения к сложной природе графена, где форма и функция неразрывно связаны. Как сказал Людвиг Витгенштейн: «Предел моего языка есть предел моего мира». В данном исследовании, расширение границ понимания диэлектрических свойств графена открывает новые горизонты в физике конденсированного состояния, позволяя увидеть мир под новым углом.

Куда же это всё ведёт?

Представленная работа, подобно тщательно настроенному инструменту, выявляет нюансы диэлектрических свойств графена, ранее остававшиеся в тени. Особый интерес представляет двойной полюс на нулевой частоте — деталь, словно шепот, намекающая на возможные решения старых головоломок, таких как эффект Казимира. Однако, стоит признать, что гармония теории и эксперимента — процесс долгий и часто болезненный. Нельзя забывать, что даже самая элегантная модель — лишь приближение к реальности, и истина, вероятно, кроется в более сложных взаимодействиях, которые пока ускользают от внимания.

Дальнейшее развитие исследований, несомненно, потребует не только углублённого теоретического анализа, но и прецизионных экспериментальных проверок. В частности, представляется важным исследовать влияние различных факторов — температуры, дефектов, внешних полей — на диэлектрическую функцию графена. Кроме того, стоит обратить внимание на возможность применения полученных результатов для создания новых материалов и устройств с необычными свойствами. Ведь даже самая незаметная деталь может сыграть решающую роль в симфонии физических явлений.

В конечном счёте, исследование графена — это не только поиск ответов на конкретные вопросы, но и стремление к более глубокому пониманию фундаментальных законов природы. И пусть путь этот будет полон трудностей и неожиданностей, ведь именно в преодолении препятствий и рождается истинная красота науки. Истинная красота, подобно идеально настроенному инструменту, звучит тихо, но уверенно.

Оригинал статьи: https://arxiv.org/pdf/2601.10478.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-18 09:34