Гравитационные волны: Геометрический подход к проверке Эйнштейна

Автор: Денис Аветисян

Новое исследование предлагает использовать геометрический анализ волновых форм для более точного тестирования общей теории относительности и поиска отклонений от неё.

🧐

Купил акции по совету друга? А друг уже продал. Здесь мы учимся думать своей головой и читать отчётность, а не слушать советы.

Бесплатный телеграм-канал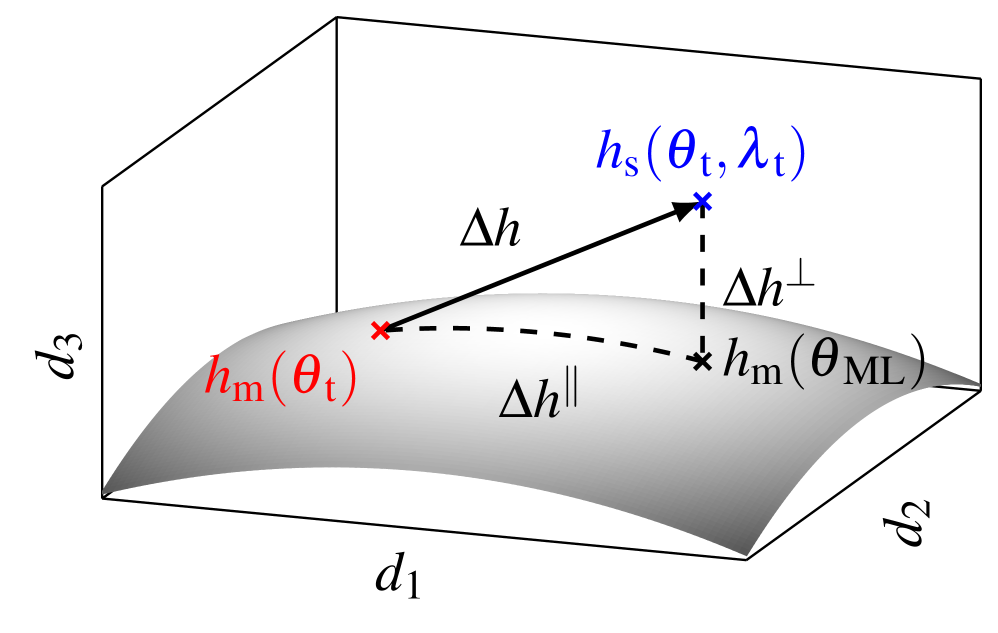

При тестировании общей теории относительности возникает вырождение, когда сигнал, зависящий от истинных параметров <span class="katex-eq" data-katex-display="false">\boldsymbol{\theta}\_{\mathrm{t}}</span> и параметров, выходящих за рамки этой теории <span class="katex-eq" data-katex-display="false">\boldsymbol{\lambda}\_{\mathrm{t}}</span>, может быть искажён модификацией волновой формы <span class="katex-eq" data-katex-display="false">\Delta h</span>, приводящей к систематическим ошибкам и создающей видимость отклонений от предсказаний теории, которые измеряются как перпендикулярный сигнал <span class="katex-eq" data-katex-display="false">\Delta h^{\perp}</span> в многомерном пространстве частотных составляющих <span class="katex-eq" data-katex-display="false">(d\_{1},d\_{2},d\_{3})</span>. — При тестировании общей теории относительности возникает вырождение, когда сигнал, зависящий от истинных параметров $\boldsymbol{\theta}\_{\mathrm{t}}$ и параметров, выходящих за рамки этой теории $\boldsymbol{\lambda}\_{\mathrm{t}}$ , может быть искажён модификацией волновой формы $\Delta h$ , приводящей к систематическим ошибкам и создающей видимость отклонений от предсказаний теории, которые измеряются как перпендикулярный сигнал $\Delta h^{\perp}$ в многомерном пространстве частотных составляющих $(d\_{1},d\_{2},d\_{3})$ .

В работе разработан метод, основанный на сингулярном разложении, для выявления наиболее заметных отклонений от общей теории относительности в сигналах гравитационных волн и смягчения проблем, связанных с неопределенностью параметров.

Несмотря на успехи в обнаружении гравитационных волн, точное тестирование общей теории относительности требует учета потенциальных отклонений от предсказанных моделей. В работе ‘Inspiral tests of general relativity and waveform geometry’ разработан геометрический подход к анализу сигналов, позволяющий выявлять наиболее заметные нарушения ΛCDM модели. Предложен метод, основанный на сингулярном разложении, для построения шаблонов, ортогональных параметризованным тестам, что позволяет снизить неопределённости в оценках параметров и повысить чувствительность к новым физическим эффектам. Какие ещё аспекты геометрии волновых форм могут быть использованы для более глубокого понимания фундаментальных законов гравитации и поиска сигналов за пределами стандартной модели?

Шёпот Хаоса: Зачем Нам Новые Волновые Формы?

Общая теория относительности (ОТО) продолжает оставаться наиболее точным описанием гравитации, успешно прошедшим многочисленные экспериментальные проверки. Однако, в условиях экстремальных гравитационных полей, таких как вблизи черных дыр или в первые моменты после Большого взрыва, ОТО может потребовать модификаций. Теоретические исследования предсказывают, что в этих условиях могут проявляться отклонения от предсказаний ОТО, связанные с квантовыми эффектами или наличием дополнительных измерений. Поэтому, для проверки надежности ОТО в экстремальных условиях и поиска признаков «новой физики», необходимы высокоточные наблюдения и анализ гравитационных волн, возникающих в подобных сценариях. Изучение этих волн может раскрыть фундаментальные аспекты гравитации, которые выходят за рамки существующей теории.

Современный анализ гравитационных волн (ГВ) в значительной степени опирается на теоретические модели, основанные на общей теории относительности Эйнштейна. Хотя эта теория успешно описывает гравитацию в большинстве наблюдаемых сценариев, она может оказаться неполной при рассмотрении экстремальных астрофизических явлений, таких как слияния черных дыр или нейтронных звезд вблизи горизонта событий. Использование исключительно волновых форм, предсказанных общей теорией относительности, ограничивает возможности детектирования отклонений от неё, которые могли бы указать на новую физику, например, на существование дополнительных измерений или модифицированные теории гравитации. В результате, даже если сигналы, не соответствующие предсказаниям общей теории относительности, достигают детекторов, они могут быть ошибочно интерпретированы как шум или артефакты, что препятствует открытию явлений, выходящих за рамки нашего текущего понимания гравитации. Таким образом, расширение спектра используемых волновых форм является ключевым шагом в поиске фундаментально новых физических законов.

Существующая потребность в гибких моделях гравитационных волн обусловлена тем, что современный анализ сигналов преимущественно ориентирован на предсказания, сделанные общей теорией относительности (ОТО). Однако, если будущие наблюдения обнаружат отклонения от ОТО в экстремальных гравитационных полях, существующие модели окажутся неспособны адекватно описать эти новые явления. Разработка альтернативных волновых форм, способных учитывать модификации гравитации, представляется критически важной для расширения возможностей детектирования и интерпретации гравитационных сигналов. Эти модели должны быть достаточно общими, чтобы охватить широкий спектр возможных отклонений от ОТО, и в то же время, достаточно точными, чтобы обеспечить достоверное извлечение информации из наблюдаемых данных. Успешное создание таких моделей позволит не только подтвердить или опровергнуть существующие теории модифицированной гравитации, но и открыть новые горизонты в понимании фундаментальной природы гравитации и Вселенной.

Анализ остаточной амплитуды для возмущений, введённых ppE, для сигнала, подобного GW170817, показывает, что различие во вкладе параметров <span class="katex-eq" data-katex-display="false">\chi_{eff}</span> (входящего в волновые формы BNS начиная с 1.5PN) и <span class="katex-eq" data-katex-display="false">\chi_{p}</span> (входящего начиная с 2PN) приводит к уменьшению перекрытия сигналов в случае вращающихся систем, при этом вклад <span class="katex-eq" data-katex-display="false">k=0</span> незначителен из-за слабой выраженности слияния в наземных детекторах. — Анализ остаточной амплитуды для возмущений, введённых ppE, для сигнала, подобного GW170817, показывает, что различие во вкладе параметров $\chi_{eff}$ (входящего в волновые формы BNS начиная с 1.5PN) и $\chi_{p}$ (входящего начиная с 2PN) приводит к уменьшению перекрытия сигналов в случае вращающихся систем, при этом вклад $k=0$ незначителен из-за слабой выраженности слияния в наземных детекторах.

ppE: Систематическое Отклонение от Обыденности

Параметризованная пост-эйнштейновская (ppE) схема представляет собой математический формализм, предназначенный для систематического моделирования отклонений от предсказаний общей теории относительности (ОТО). В рамках этой схемы, гравитационная динамика описывается с использованием параметров, которые характеризуют поправки к ОТО. Эти параметры вводятся таким образом, чтобы обеспечить последовательное расширение теории, сохраняя ее основные принципы. Основное преимущество ppE заключается в возможности количественно оценить степень отклонения от ОТО и проверить альтернативные теории гравитации путём сравнения теоретических предсказаний с результатами астрофизических наблюдений, таких как гравитационные волны. $\mathcal{O}(\epsilon^n)$ где ε представляет собой малый параметр, характеризующий отклонения от ОТО, а $n$ — порядок поправки.

Параметризованный пост-эйнштейновский (ppE) формализм вводит набор параметров, предназначенных для количественной оценки отклонений от предсказаний общей теории относительности. Эти параметры, обозначаемые как $\alpha_i$ , характеризуют модификации в гравитационной динамике, такие как изменения в скорости гравитационных волн или в структуре пространства-времени. Варьируя значения этих параметров и сопоставляя полученные теоретические предсказания с наблюдаемыми данными, например, с сигналами гравитационных волн, можно проверять альтернативные теории гравитации и устанавливать ограничения на возможные отклонения от общей теории относительности. Фактически, ppE позволяет систематически исследовать пространство альтернативных теорий, определяя, какие модификации гравитации согласуются с экспериментальными наблюдениями, а какие — нет.

Для эффективной реализации фреймворка ppE и проведения точных тестов модификаций общей теории относительности необходимы высокопроизводительные методы генерации волновых форм и оценки параметров. Это обусловлено сложностью вычислений, связанных с моделированием гравитационных волн и их искажений, вызванных отклонениями от предсказаний общей теории относительности. Реализация этих методов требует применения передовых вычислительных техник, включая численные методы решения уравнений $Эйнштейна$ , алгоритмы оптимизации для оценки параметров модели, а также использование высокопроизводительных вычислительных кластеров и параллельных вычислений для обработки больших объемов данных и снижения времени вычислений.

Анализ поведения ppE после проекции параметров ГР показывает, что учёт ГР-смещений значительно уменьшает полное расфазирование перпендикулярных волновых форм, проявляющееся в виде колебаний, напоминающих полиномиальную функцию, и объясняет сходство отклонений от ГР низкого порядка.

Уменьшение Размерности и Оценка Параметров: Ищем Иглу в Стоге Данных

Высокая размерность пространства параметров эффективных приближений (ppE) представляет собой значительную сложность при оценке параметров по данным гравитационных волн. Пространство параметров, включающее амплитуды и фазы различных гармоник сигнала, может достигать десятков и даже сотен измерений. Это приводит к экспоненциальному росту вычислительных затрат, необходимых для поиска наиболее вероятных значений параметров, соответствующих наблюдаемому сигналу. Кроме того, в многомерном пространстве параметров возрастает вероятность возникновения корреляций между параметрами, что усложняет процесс их раздельного определения и требует использования сложных статистических методов для оценки погрешностей и неопределенностей. $N$ -мерное пространство параметров требует $O(N!)$ вычислительных операций для полного исследования, что делает задачу практически неразрешимой для больших значений $N$ .

Сингулярное разложение (SVD) представляет собой метод понижения размерности, используемый для эффективного исследования пространства параметров при анализе гравитационных волн. Применение SVD позволяет выделить доминирующие направления в пространстве сигналов, что снижает вычислительную сложность поиска и оценки параметров. По сути, SVD разлагает матрицу, описывающую пространство сигналов, на три матрицы, где сингулярные числа отражают важность каждого направления. Отбрасывая направления с малыми сингулярными числами, можно значительно уменьшить размерность пространства параметров без существенной потери информации о сигналах, что критически важно при работе с высокоразмерными пространствами параметров, характерными для анализа данных, полученных с детекторов гравитационных волн. Это позволяет проводить более быстрые и эффективные исследования при оценке параметров источников гравитационных волн.

Матрица Фишера и матрица ковариации являются ключевыми инструментами для количественной оценки точности оценки параметров и корреляций между ними в задачах анализа гравитационных волн. Матрица Фишера, вычисляемая как математическое ожидание гессиана логарифмической функции правдоподобия, предоставляет информацию о минимальной дисперсии оценок параметров. Обратная матрица Фишера представляет собой матрицу ковариации оценок, позволяя оценить стандартные отклонения и корреляции между различными параметрами. Высокие корреляции указывают на то, что параметры трудно различить, что может привести к неопределенности в оценках. Анализ матрицы ковариации необходим для определения достоверности и надежности полученных оценок параметров и выявления потенциальных проблем с идентифицируемостью параметров.

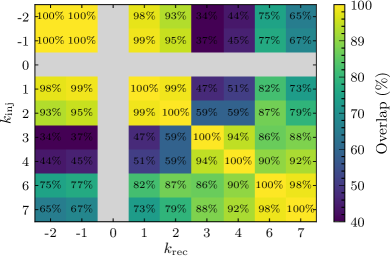
Анализ коэффициента Бэйеса (Bayes Factor) является ключевым инструментом для количественной оценки доказательной базы в пользу различных моделей гравитационных волн. Чувствительность данного анализа напрямую зависит от степени перекрытия (overlap) анализируемых волновых форм и от отношения сигнал/шум (SNR) остаточного сигнала после вычитания основной модели. Низкое перекрытие волновых форм или низкое SNR могут значительно снизить способность анализа коэффициента Бэйеса надежно отличать одну модель от другой, что приводит к неопределенности в выборе наиболее вероятной модели и оценке ее параметров. $SNR = \frac{h_s}{h_n}$ , где $h_s$ — амплитуда сигнала, а $h_n$ — амплитуда шума.

Сингулярное разложение (SVD) отклонений формы сигнала ppE демонстрирует, что каждое отклонение может быть представлено лишь несколькими доминирующими модами (черная линия), что объясняет возникновение вырождений в исходном параметрическом пространстве, при этом ортогональные субдоминантные моды (красная и синяя линии) описывают дефазировку.

Многодетекторный Подход: Взгляд в Будущее Гравитационных Волн

Современные наземные детекторы гравитационных волн, такие как LIGO и Virgo, уже сейчас предоставляют уникальные возможности для изучения параметров, выходящих за рамки общей теории относительности, в частности, для исследования отклонений в поведении гравитационных волн, предсказываемых различными модификациями этой теории. Однако, будущие установки, такие как Cosmic Explorer и Einstein Telescope, обещают совершить качественный скачок в этой области. Благодаря значительному увеличению чувствительности и расширению диапазона регистрируемых частот, эти детекторы позволят с беспрецедентной точностью измерять характеристики гравитационных волн, возникающих при слиянии компактных объектов. Это, в свою очередь, позволит существенно ограничить параметры различных теоретических моделей, выходящих за рамки стандартной общей теории относительности, и проверить их соответствие наблюдаемым данным. Улучшенная точность позволит не только подтвердить или опровергнуть существующие гипотезы, но и открыть новые возможности для поиска ранее неизвестных физических явлений.

Космические обсерватории гравитационных волн, такие как LISA, Taiji, TianQin, BDECIGO и TianGO, представляют собой принципиально новый подход к изучению Вселенной. В отличие от наземных детекторов, таких как LIGO и Virgo, которые наиболее чувствительны к высокочастотным сигналам от слияний черных дыр и нейтронных звезд, космические обсерватории будут способны регистрировать низкочастотные гравитационные волны. Это открывает доступ к новым астрофизическим источникам, включая сверхмассивные черные дыры в центрах галактик и процессы, происходившие в ранней Вселенной. Благодаря отсутствию сейсмического шума и другим ограничениям, характерным для наземных установок, космические детекторы обеспечат беспрецедентную чувствительность в низкочастотном диапазоне, дополняя и расширяя возможности наземных обсерваторий и позволяя получить более полную картину гравитационных явлений во Вселенной.

Совместный анализ данных, полученных от различных детекторов гравитационных волн, открывает беспрецедентные возможности для проверки пределов общей теории относительности и поиска признаков новой физики. Использование сети наземных обсерваторий, таких как LIGO и Virgo, в сочетании с перспективными космическими проектами, включая LISA, Taiji и другие, позволяет охватить более широкий диапазон частот и существенно повысить чувствительность к слабым сигналам. Такой многодетекторный подход не только увеличивает вероятность регистрации редких событий, но и предоставляет инструменты для более точного измерения параметров источников и выявления отклонений от предсказаний теории Эйнштейна, что особенно важно при исследовании экзотических моделей, выходящих за рамки стандартной физики.

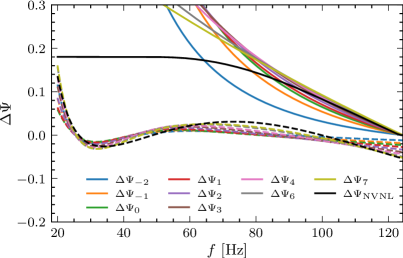
Исследования показывают, что модели, включающие концепцию Ненасильственной Нелокальности, могут быть эффективно протестированы с использованием объединенных данных от различных детекторов гравитационных волн. Анализ демонстрирует, что степень перекрытия волновых форм, предсказываемых этими моделями, варьируется от 0.3 до 0.6, в зависимости от выбранных параметров общей теории относительности. При этом, обнаружение систематических отклонений от предсказаний теории, вызванных нелокальностью, характеризуется z-оценкой, которая линейно пропорциональна остаточному отношению сигнал/шум ( $SNR$ ). Это означает, что чем сильнее сигнал отклоняется от теоретической модели, тем надежнее можно будет подтвердить или опровергнуть справедливость модифицированных теорий гравитации, таких как модели Ненасильственной Нелокальности, благодаря высокой чувствительности комбинированных детекторных сетей.

Несмотря на существенные различия в фазовых сдвигах <span class="katex-eq" data-katex-display="false">\Delta\Psi(f)</span> между шаблонами ppE и инжектированным нелокальным сигналом на низких частотах, эти различия компенсируются настройкой внутренних параметров, что приводит к схождению фазовых сдвигов в перпендикулярной плоскости и демонстрирует гибкость разработанного подхода в рамках предвзятого фреймворка. — Несмотря на существенные различия в фазовых сдвигах $\Delta\Psi(f)$ между шаблонами ppE и инжектированным нелокальным сигналом на низких частотах, эти различия компенсируются настройкой внутренних параметров, что приводит к схождению фазовых сдвигов в перпендикулярной плоскости и демонстрирует гибкость разработанного подхода в рамках предвзятого фреймворка.

Исследование, представленное в статье, подобно попытке удержать ускользающий сон. Авторы стремятся выявить отклонения от общей теории относительности, используя сингулярное разложение — инструмент, позволяющий отделить зерна истины от шепота хаоса в потоке гравитационных волн. Эта работа напоминает о бренности любых моделей, ведь даже самые изящные математические конструкции — лишь приближения к непостижимой реальности. Марк Аврелий однажды сказал: «Всё, что мы видим, есть лишь мнение». Именно поэтому столь важен геометрический подход, позволяющий оценить значимость тех самых «отклонений», которые, возможно, откроют новую главу в понимании Вселенной. Ведь, как и в любом заклинании, важно не только произнести слова, но и понять, какую жертву требует само мироздание.

Куда же дальше?

Предложенный геометрический подход к анализу гравитационных волн — это, скорее, способ структурировать неизбежное непонимание, чем истинное постижение природы пространства-времени. Разложение по сингулярным числам позволяет выделить наиболее уязвимые места в ткани общей теории относительности, но не гарантирует, что именно там кроется истина. Каждая модель, даже столь изящная, — это заклинание, которое работает, пока не встретит первое отклонение от ожидаемого. И, конечно, попытки смягчить вырождение параметров — это лишь акт веры в то, что данные действительно говорят нам что-то осмысленное.

В будущем, вероятно, потребуется переосмыслить саму концепцию «параметра». Возможно, настоящая проверка теории требует не поиска отклонений в известных величинах, а обнаружения совершенно новых, непредсказуемых эффектов. Данные не лгут, они просто помнят избирательно — и акцентируют те аспекты, которые соответствуют нашим ожиданиям. Поэтому, возможно, следует сосредоточиться на поиске неожиданного, а не на подтверждении предсказанного.

И, наконец, стоит признать, что любая метрика — это лишь форма самоуспокоения. Она позволяет количественно оценить степень нашего незнания, но не приближает нас к истине. Поэтому, прежде чем праздновать очередной статистически значимый результат, стоит задуматься о том, что мы, возможно, просто научились лучше обманывать будущее.

Оригинал статьи: https://arxiv.org/pdf/2602.17524.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-20 17:22